число параметров уравнения регрессии
Корреляция и регрессия
Для наших данных система уравнений имеет вид:
10a + 356b = 49
356a + 2135b = 9485
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17
1. Параметры уравнения регрессии.
Выборочные средние.
1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bxp ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (7;0.05) = 1.895
Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения ei с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения ei (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости ei от ei-1.
R — значит регрессия
Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.
Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.
Введение в регрессионный анализ
Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей
минимальна.
Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.
Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений
вокруг регрессии
является дисперсия.
Линейная регрессия
Уравнения линейной регрессии можно записать в виде
В матричном виде это выгладит
Случайная величина может быть интерпретирована как сумма из двух слагаемых:
Ограничения линейной регрессии
Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.
Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.
Неоднородность дисперсии
При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.
Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.
Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.
В этой формуле — коэффициент взаимной детерминации между
и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.
Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.
Как преодолеть эти ограничения
Нарушения одной или нескольких ограничений еще не приговор.
К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.
Линейная регрессия плюсов на Хабре
Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.
Загружает данные из tsv файла.
Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.
В первой строке мы задаем параметры линейной регрессии. Строка points
. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points
Перейдем теперь к расшифровке полученных результатов.
Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.
Проверим значения параметров линейной регрессии.
Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.
И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.
В заключение
Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.
Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.
Оценка параметров уравнения регреcсии. Пример
Задание:
По группе предприятий, выпускающих один и тот же вид продукции, рассматриваются функции издержек:
y = α + βx;
y = α x β ;
y = α β x ;
y = α + β / x;
где y – затраты на производство, тыс. д. е.
x – выпуск продукции, тыс. ед.
1. Уравнение имеет вид y = α + βx
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 78 | 133 | 6084 | 17689 | 10374 | 142.16 | 115.98 | 83.83 | 1 |
| 82 | 148 | 6724 | 21904 | 12136 | 148.61 | 17.9 | 0.37 | 9 |
| 87 | 134 | 7569 | 17956 | 11658 | 156.68 | 95.44 | 514.26 | 64 |
| 79 | 154 | 6241 | 23716 | 12166 | 143.77 | 104.67 | 104.67 | 0 |
| 89 | 162 | 7921 | 26244 | 14418 | 159.9 | 332.36 | 4.39 | 100 |
| 106 | 195 | 11236 | 38025 | 20670 | 187.33 | 2624.59 | 58.76 | 729 |
| 67 | 139 | 4489 | 19321 | 9313 | 124.41 | 22.75 | 212.95 | 144 |
| 88 | 158 | 7744 | 24964 | 13904 | 158.29 | 202.51 | 0.08 | 81 |
| 73 | 152 | 5329 | 23104 | 11096 | 134.09 | 67.75 | 320.84 | 36 |
| 87 | 162 | 7569 | 26244 | 14094 | 156.68 | 332.36 | 28.33 | 64 |
| 76 | 159 | 5776 | 25281 | 12084 | 138.93 | 231.98 | 402.86 | 9 |
| 115 | 173 | 13225 | 29929 | 19895 | 201.86 | 854.44 | 832.66 | 1296 |
| 0 | 0 | 0 | 16.3 | 20669.59 | 265.73 | 6241 | ||
| 1027 | 1869 | 89907 | 294377 | 161808 | 1869 | 25672.31 | 2829.74 | 8774 |
2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции
Анализ точности определения оценок коэффициентов регрессии
S a = 0.1712
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-20.41;56.24)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается
Fkp = 4.84
Поскольку F > Fkp, то коэффициент детерминации статистически значим
Решаем уравнение простой линейной регрессии
В статье рассматривается несколько способов определения математического уравнения линии простой (парной) регрессии.
Все рассматриваемые здесь способы решения уравнения основаны на методе наименьших квадратов. Обозначим способы следующим образом:
Весь код, приведенный в статье, написан на языке python 2.7 с использованием Jupyter Notebook. Исходный код и файл с данными выборки выложен на гитхабе
Статья в большей степени ориентирована как на начинающих, так и на тех, кто уже понемногу начал осваивать изучение весьма обширного раздела в искусственном интеллекте — машинного обучения.
Для иллюстрации материала используем очень простой пример.
Условия примера
У нас есть пять значений, которые характеризуют зависимость Y от X (Таблица №1):
Таблица №1 «Условия примера»
Будем считать, что значения — это месяц года, а
— выручка в этом месяце. Другими словами, выручка зависит от месяца года, а
— единственный признак, от которого зависит выручка.
Пример так себе, как с точки зрения условной зависимости выручки от месяца года, так и с точки зрения количества значений — их очень мало. Однако такое упрощение позволит, что называется на пальцах, объяснить, не всегда с легкостью, усваиваемый новичками материал. А также простота чисел позволит без весомых трудозатрат, желающим, порешать пример на «бумаге».
Предположим, что приведенная в примере зависимость, может быть достаточно хорошо аппроксимирована математическим уравнением линии простой (парной) регрессии вида:
где — это месяц, в котором была получена выручка,
— выручка, соответствующая месяцу,
и
— коэффициенты регрессии оцененной линии.
Отметим, что коэффициент часто называют угловым коэффициентом или градиентом оцененной линии; представляет собой величину, на которую изменится
при изменении
.
Очевидно, что наша задача в примере — подобрать в уравнении такие коэффициенты и
, при которых отклонения наших расчетных значений выручки по месяцам от истинных ответов, т.е. значений, представленных в выборке, будут минимальны.
Метод наименьших квадратов
В соответствии с методом наименьших квадратов, отклонение стоит рассчитывать, возводя его в квадрат. Подобный прием позволяет избежать взаимного погашения отклонений, в том случае, если они имеют противоположные знаки. Например, если в одном случае, отклонение составляет +5 (плюс пять), а в другом -5 (минус пять), то сумма отклонений взаимно погасится и составит 0 (ноль). Можно и не возводить отклонение в квадрат, а воспользоваться свойством модуля и тогда у нас все отклонения будут положительными и будут накапливаться. Мы не будем останавливаться на этом моменте подробно, а просто обозначим, что для удобства расчетов, принято возводить отклонение в квадрат.
Вот так выглядит формула, с помощью которой мы определим наименьшую сумму квадратов отклонений (ошибки):
где — это функция аппроксимации истинных ответов (то есть посчитанная нами выручка),
— это истинные ответы (предоставленная в выборке выручка),
— это индекс выборки (номер месяца, в котором происходит определение отклонения)
Продифференцируем функцию, определим уравнения частных производных и будем готовы перейти к аналитическому решению. Но для начала проведем небольшой экскурс о том, что такое дифференцирование и вспомним геометрический смысл производной.
Дифференцирование
Дифференцированием называется операция по нахождению производной функции.
Для чего нужна производная? Производная функции характеризует скорость изменения функции и указывает нам ее направление. Если производная в заданной точке положительна, то функция возрастает, в обратном случае — функция убывает. И чем больше значение производной по модулю, тем выше скорость изменения значений функции, а также круче угол наклона графика функции.
Например, в условиях декартовой системы координат, значение производной в точке M(0,0) равное +25 означает, что в заданной точке, при смещении значения вправо на условную единицу, значение
возрастает на 25 условных единиц. На графике это выглядит, как достаточно крутой угол подъема значений
с заданной точки.
Другой пример. Значение производной равное -0,1 означает, что при смещении на одну условную единицу, значение
убывает всего лишь на 0,1 условную единицу. При этом, на графике функции, мы можем наблюдать едва заметный наклон вниз. Проводя аналогию с горой, то мы как будто очень медленно спускаемся по пологому склону с горы, в отличие от предыдущего примера, где нам приходилось брать очень крутые вершины:)
Таким образом, проведя дифференцирование функции по коэффициентам
и
, определим уравнения частных производных 1-го порядка. После определения уравнений, мы получим систему из двух уравнений, решив которую мы сможем подобрать такие значения коэффициентов
и
, при которых значения соответствующих производных в заданных точках изменяются на очень и очень малую величину, а в случае с аналитическим решением не изменяются вовсе. Другими словами, функция ошибки при найденных коэффициентах достигнет минимума, так как значения частных производных в этих точках будут равны нулю.
Итак, по правилам дифференцирования уравнение частной производной 1-го порядка по коэффициенту примет вид:
уравнение частной производной 1-го порядка по примет вид:
В итоге мы получили систему уравнений, которая имеет достаточно простое аналитическое решение:
\begin
\begin
na + b\sum\limits_
\\
\sum\limits_
\end
\end
Прежде чем решать уравнение, предварительно загрузим, проверим правильность загрузки и отформатируем данные.
Загрузка и форматирование данных
Необходимо отметить, что в связи с тем, что для аналитического решения, а в дальнейшем для градиентного и стохастического градиентного спуска, мы будем применять код в двух вариациях: с использованием библиотеки NumPy и без её использования, то нам потребуется соответствующее форматирование данных (см. код).
Визуализация
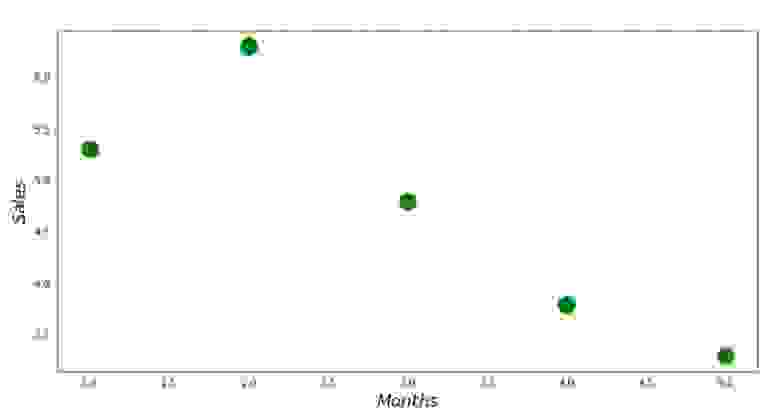
Теперь, после того, как мы, во-первых, загрузили данные, во-вторых, проверили правильность загрузки и наконец отформатировали данные, проведем первую визуализацию. Часто для этого используют метод pairplot библиотеки Seaborn. В нашем примере, ввиду ограниченности цифр нет смысла применять библиотеку Seaborn. Мы воспользуемся обычной библиотекой Matplotlib и посмотрим только на диаграмму рассеяния.
График №1 «Зависимость выручки от месяца года»
Аналитическое решение
Воспользуемся самыми обычными инструментами в python и решим систему уравнений:
\begin
\begin
na + b\sum\limits_
\\
\sum\limits_
\end
\end
По правилу Крамера найдем общий определитель, а также определители по и по
, после чего, разделив определитель по
на общий определитель — найдем коэффициент
, аналогично найдем коэффициент
.
Вот, что у нас получилось:
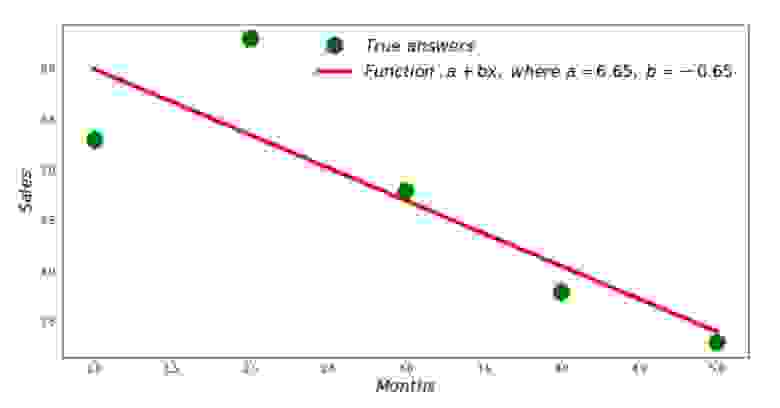
Итак, значения коэффициентов найдены, сумма квадратов отклонений установлена. Нарисуем на гистограмме рассеяния прямую линию в соответствии с найденными коэффициентами.
График №2 «Правильные и расчетные ответы»
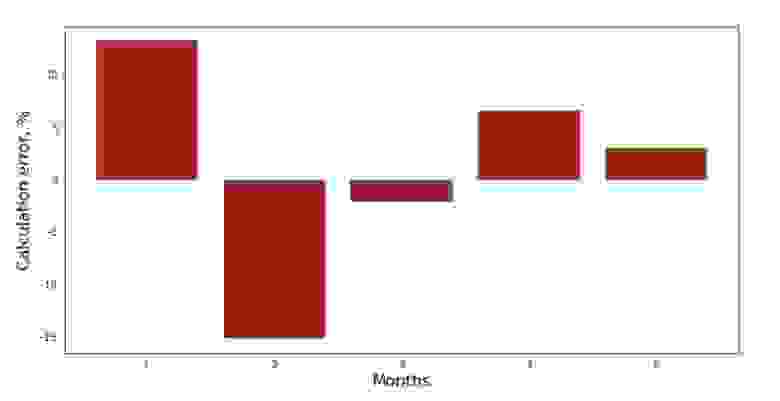
Можно посмотреть на график отклонений за каждый месяц. В нашем случае, какой-либо значимой практической ценности мы из него не вынесем, но удовлетворим любопытство в том, насколько хорошо, уравнение простой линейной регрессии характеризует зависимость выручки от месяца года.
График №3 «Отклонения, %»
Не идеально, но нашу задачу мы выполнили.
Напишем функцию, которая для определения коэффициентов и
использует библиотеку NumPy, точнее — напишем две функции: одну с использованием псевдообратной матрицы (не рекомендуется на практике, так как процесс вычислительно сложный и нестабильный), другую с использованием матричного уравнения.
Сравним время, которое было затрачено на определение коэффициентов и
, в соответствии с 3-мя представленными способами.
На небольшом количестве данных, вперед выходит «самописная» функция, которая находит коэффициенты методом Крамера.
Теперь можно перейти к другим способам нахождения коэффициентов и
.
Градиентный спуск
Для начала определим, что такое градиент. По-простому, градиент — это отрезок, который указывает направление максимального роста функции. По аналогии с подъемом в гору, то куда смотрит градиент, там и есть самый крутой подъем к вершине горы. Развивая пример с горой, вспоминаем, что на самом деле нам нужен самый крутой спуск, чтобы как можно быстрее достичь низины, то есть минимума — места где функция не возрастает и не убывает. В этом месте производная будет равна нулю. Следовательно, нам нужен не градиент, а антиградиент. Для нахождения антиградиента нужно всего лишь умножить градиент на -1 (минус один).
Обратим внимание на то, что функция может иметь несколько минимумов, и опустившись в один из них по предложенному далее алгоритму, мы не сможем найти другой минимум, который возможно находится ниже найденного. Расслабимся, нам это не грозит! В нашем случае мы имеем дело с единственным минимумом, так как наша функция на графике представляет собой обычную параболу. А как мы все должны прекрасно знать из школьного курса математики — у параболы существует только один минимум.
После того, как мы выяснили для чего нам потребовался градиент, а также то, что градиент — это отрезок, то есть вектор с заданными координатами, которые как раз являются теми самыми коэффициентами и
мы можем реализовать градиентный спуск.
Перед запуском, предлагаю прочитать буквально несколько предложений об алгоритме спуска:
Мы погрузились на самое дно Марианской впадины и там обнаружили все те же значения коэффициентов и
, что собственно и следовало ожидать.
Совершим еще одно погружение, только на этот раз, начинкой нашего глубоководного аппарата будут иные технологии, а именно библиотека NumPy.

Значения коэффициентов и
неизменны.
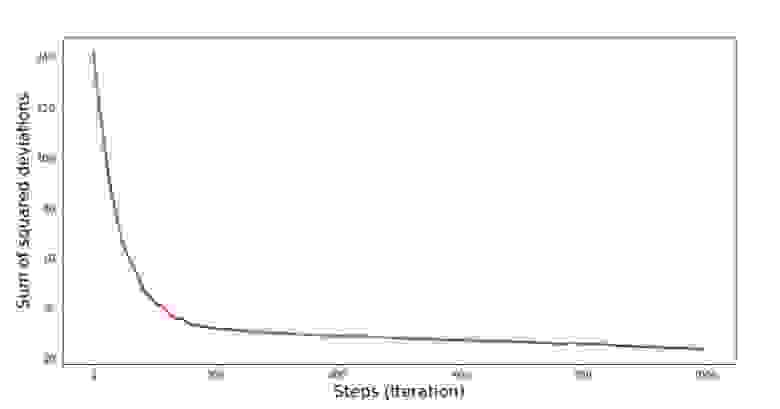
Посмотрим на то, как изменялась ошибка при градиентном спуске, то есть как изменялась сумма квадратов отклонений с каждым шагом.
График №4 «Сумма квадратов отклонений при градиентном спуске»
На графике мы видим, что с каждым шагом ошибка уменьшается, а спустя какое-то количество итераций наблюдаем практически горизонтальную линию.
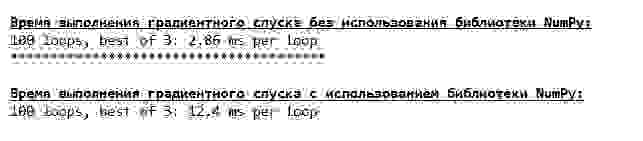
Напоследок оценим разницу во времени исполнения кода:
Возможно мы делаем что-то не то, но опять простая «самописная» функция, которая не использует библиотеку NumPy опережает по времени выполнения расчетов функцию, использующую библиотеку NumPy.
Но мы не стоим на месте, а двигаемся в сторону изучения еще одного увлекательного способа решения уравнения простой линейной регрессии. Встречайте!
Стохастический градиентный спуск
Для того, чтобы быстрее понять принцип работы стохастического градиентного спуска, лучше определить его отличия от обычного градиентного спуска. Мы, в случае с градиентным спуском, в уравнениях производных от и
использовали суммы значений всех признаков и истинных ответов, имеющихся в выборке (то есть суммы всех
и
). В стохастическом градиентном спуске мы не будем использовать все значения, имеющиеся в выборке, а вместо этого, псевдослучайным образом выберем так называемый индекс выборки и используем его значения.
Например, если индекс определился за номером 3 (три), то мы берем значения и
, далее подставляем значения в уравнения производных и определяем новые координаты. Затем, определив координаты, мы опять псевдослучайным образом определяем индекс выборки, подставляем значения, соответствующие индексу в уравнения частных производных, по новому определяем координаты
и
и т.д. до
позеленения сходимости. На первый взгляд, может показаться, как это вообще может работать, однако работает. Правда стоит отметить, что не с каждым шагом уменьшается ошибка, но тенденция безусловно имеется.
Каковы преимущества стохастического градиентного спуска перед обычным? В случае, если у нас размер выборки очень велик и измеряется десятками тысяч значений, то значительно проще обработать, допустим случайную тысячу из них, нежели всю выборку. Вот в этом случае и запускается стохастический градиентный спуск. В нашем случае мы конечно же большой разницы не заметим.
Смотрим внимательно на коэффициенты и ловим себя на вопросе «Как же так?». У нас получились другие значения коэффициентов и
. Может быть стохастический градиентный спуск нашел более оптимальные параметры уравнения? Увы, нет. Достаточно посмотреть на сумму квадратов отклонений и увидеть, что при новых значениях коэффициентов, ошибка больше. Не спешим отчаиваться. Построим график изменения ошибки.
График №5 «Сумма квадратов отклонений при стохастическом градиентном спуске»
Посмотрев на график, все становится на свои места и сейчас мы все исправим.
Итак, что же произошло? Произошло следующее. Когда мы выбираем случайным образом месяц, то именно для выбранного месяца наш алгоритм стремится уменьшить ошибку в расчете выручки. Затем выбираем другой месяц и повторяем расчет, но ошибку уменьшаем уже для второго выбранного месяца. А теперь вспомним, что у нас первые два месяца существенно отклоняются от линии уравнения простой линейной регрессии. Это значит, что когда выбирается любой из этих двух месяцев, то уменьшая ошибку каждого из них, наш алгоритм серьезно увеличивает ошибку по всей выборке. Так что же делать? Ответ простой: надо уменьшить шаг спуска. Ведь уменьшив шаг спуска, ошибка так же перестанет «скакать» то вверх, то вниз. Вернее, ошибка «скакать» не перестанет, но будет это делать не так прытко:) Проверим.
График №6 «Сумма квадратов отклонений при стохастическом градиентном спуске (80 тыс. шагов)»
Значения коэффициентов улучшились, но все равно не идеальны. Гипотетически это можно поправить таким образом. Выбираем, например, на последних 1000 итерациях значения коэффициентов, с которыми была допущена минимальная ошибка. Правда нам для этого придется записывать еще и сами значения коэффициентов. Мы не будем этого делать, а лучше обратим внимание на график. Он выглядит гладким, и ошибка как будто уменьшается равномерно. На самом деле это не так. Посмотрим на первые 1000 итераций и сравним их с последними.
График №7 «Сумма квадратов отклонений SGD (первые 1000 шагов)»
График №8 «Сумма квадратов отклонений SGD (последние 1000 шагов)»
В самом начале спуска мы наблюдаем достаточно равномерное и крутое уменьшение ошибки. На последних итерациях мы видим, что ошибка ходит вокруг да около значения в 1,475 и в некоторые моменты даже равняется этому оптимальному значению, но потом все равно уходит ввысь… Повторюсь, можно записывать значения коэффициентов и
, а потом выбрать те, при которых ошибка минимальна. Однако у нас возникла проблема посерьезнее: нам пришлось сделать 80 тыс. шагов (см. код), чтобы получить значения, близкие к оптимальным. А это, уже противоречит идее об экономии времени вычислений при стохастическом градиентном спуске относительно градиентного. Что можно поправить и улучшить? Не трудно заметить, что на первых итерациях мы уверенно идем вниз и, следовательно, нам стоит оставить большой шаг на первых итерациях и по мере продвижения вперед шаг уменьшать. Мы не будем этого делать в этой статье — она и так уже затянулась. Желающие могут и сами подумать, как это сделать, это не сложно 🙂
Теперь выполним стохастический градиентный спуск, используя библиотеку NumPy (и не будем спотыкаться о камни, которые мы выявили раннее)
Значения получились почти такими же, как и при спуске без использования NumPy. Впрочем, это логично.
Узнаем сколько же времени занимали у нас стохастические градиентные спуски.
Чем дальше в лес, тем темнее тучи: опять «самописная» формула показывает лучший результат. Все это наводит на мысли о том, что должны существовать еще более тонкие способы использования библиотеки NumPy, которые действительно ускоряют операции вычислений. В этой статье мы о них уже не узнаем. Будет о чем подумать на досуге:)
Резюмируем
Перед тем как резюмировать, хотелось бы ответить на вопрос, который скорее всего, возник у нашего дорогого читателя. Для чего, собственно, такие «мучения» со спусками, зачем нам ходить по горе вверх и вниз (преимущественно вниз), чтобы найти заветную низину, если в наших руках такой мощный и простой прибор, в виде аналитического решения, который мгновенно телепортирует нас в нужное место?
Ответ на этот вопрос лежит на поверхности. Сейчас мы разбирали очень простой пример, в котором истинный ответ зависит от одного признака
. В жизни такое встретишь не часто, поэтому представим, что у нас признаков 2, 30, 50 или более. Добавим к этому тысячи, а то и десятки тысяч значений для каждого признака. В этом случае аналитическое решение может не выдержать испытания и дать сбой. В свою очередь градиентный спуск и его вариации будут медленно, но верно приближать нас к цели — минимуму функции. А на счет скорости не волнуйтесь — мы наверняка еще разберем способы, которые позволят нам задавать и регулировать длину шага (то есть скорость).
А теперь собственно краткое резюме.
Во-первых, надеюсь, что изложенный в статье материал, поможет начинающим «дата сайнтистам» в понимании того, как решать уравнения простой (и не только) линейной регрессии.
Во-вторых, мы рассмотрели несколько способов решения уравнения. Теперь, в зависимости от ситуации, мы можем выбрать тот, который лучше всего подходит для решения поставленной задачи.
В-третьих, мы увидели силу дополнительных настроек, а именно длины шага градиентного спуска. Этим параметром нельзя пренебрегать. Как было подмечено выше, с целью сокращения затрат на проведение вычислений, длину шага стоит изменять по ходу спуска.
В-четвертых, в нашем случае, «самописные» функции показали лучший временной результат вычислений. Вероятно, это связано с не самым профессиональным применением возможностей библиотеки NumPy. Но как бы то ни было, вывод напрашивается следующий. С одной стороны, иногда стоит подвергать сомнению устоявшиеся мнения, а с другой — не всегда стоит все усложнять — наоборот иногда эффективнее оказывается более простой способ решения задачи. А так как цель у нас была разобрать три подхода в решении уравнения простой линейной регрессии, то использование «самописных» функций нам вполне хватило.
Предыдущая работа автора — «Исследуем утверждение центральной предельной теоремы с помощью экспоненциального распределения»
Следующая работа автора — «Приводим уравнение линейной регрессии в матричный вид»