Что было получено леонардом эйлером в 1755 году
Леонард Эйлер
Леонард Эйлер (1707-1783) – швейцарский, немецкий и российский математик и механик, внесший огромный вклад в развитие этих наук (а также физики, астрономии и ряда прикладных наук). За годы своей жизни издал свыше 850 работ, касающихся самых разных областей.
Эйлер глубоко исследовал ботанику, медицину, химию, воздухоплавание, теорию музыки, множество европейских и древних языков. Был членом многих академий наук, являясь первым российским членом Американской академии искусств и наук.
В биографии Леонарда Эйлера есть множество интересных фактов, о которых мы расскажем в данной статье.
Итак, перед вами краткая биография Эйлера.
Биография Леонарда Эйлера
Леонард Эйлер появился на свет 15 апреля 1707 г. в швейцарском городе Базеле. Он рос и воспитывался в семье пастора Пауля Эйлера и его супруги Маргареты Брукер.
Стоит заметить, что отец будущего ученого увлекался математикой. На протяжении первых 2-х лет учебы в университете он посещал курсы известного математика Якоба Бернулли.
Детство и юность
Первые годы детства Леонарда прошли в селении Рихен, куда семейство Эйлеров переехало вскоре после рождения сына.
Начальное образование мальчик получил под руководством своего отца. Любопытно, что у него достаточно рано проявились математические способности.
Когда Леонарду было около 8 лет родители отправили его учиться в гимназию, которая находилась в Базеле. В тот момент биографии он проживал вместе с бабушкой по материнской линии.
В 13-летнем возрасте талантливому ученику разрешили посещать лекции в Базельском университете. Леонард настолько хорошо и быстро учился, что на него вскоре обратил внимание профессор Иоганн Бернулли, который был братом Якоба Бернулли.
Профессор предоставил юноше множество математических трудов и даже разрешил ему приходить к нему домой по субботам, для разъяснения труднопонимаемого материала.
Через несколько месяцев подросток успешно сдал экзамены в Базельский университет на факультет искусств. После 3-х лет обучения в вузе он удостоился ученой степени магистра, выступив с лекцией на латыни, в ходе которой сравнил систему Декарта с натуральной философией Ньютона.
В скором времени, желая угодить отцу, Леонард поступил на богословский факультет, продолжая активно заниматься математикой. Интересен факт, что позже Эйлер-старший разрешил сыну связать свою жизнь с наукой, поскольку осознавал его одаренность.
В то время биографии Леонард Эйлер опубликовал несколько научных работ, включая «Диссертацию по физике о звуке». Данная работа участвовала в конкурсе на освободившуюся должность профессора физики.
Несмотря на положительный отзыв, 19-летнего Леонарда сочли чересчур молодым, чтобы доверить ему профессорскую кафедру.
Вскоре Эйлер получил заманчивое приглашение от представителей Санкт-Петербургской академии наук, которая только находилась на пути своего становления и остро нуждалась в талантливых ученых.
Научная карьера в Санкт-Петербурге
В 1727 г. Леонард Эйлер приехал в Санкт-Петербург, где стал адъюнктом высшей математики. Российское правительство выделило ему квартиру и определило оклад в размере 300 рублей в год.
Математик сразу же начал учить русский язык, который смог освоить в сжатые сроки.
Позднее Эйлер подружился с Кристианом Гольдбахом – постоянным секретарем академии. Она вели активную переписку, которая сегодня признана важным источником по истории науки в 18 веке.
Данный период биографии Леонарда был необычайно плодотворен. Благодаря своим трудам он быстро приобрел мировую известность и признание со стороны научного сообщества.
Политическая нестабильность в России, прогрессировавшая после смерти императрицы Анны Ивановны, вынудила ученого выехать из Санкт-Петербурга.
В 1741 г., по приглашению прусского монарха Фридриха 2, Леонард Эйлер вместе с семьей отправился в Берлин. Немецкий король хотел основать академию наук, поэтому был заинтересован в услугах ученого.
Работа в Берлине
Когда в 1746 г. в Берлине открылась своя академия, Леонард занял должность руководителя математического отделения. Кроме этого ему доверили следить за обсерваторией, а также решать кадровые и финансовые вопросы.
Авторитет Эйлера, а с ним и материальное благополучие, с каждым годом росли. В результате, он стал настолько богат, что смог купить роскошное имение в Шарлоттенбурге.
Отношения Леонарда с Фридрихом 2 было сложно назвать простыми. Некоторые биографы математика полагают, что Эйлер держал обиду на прусского монарха за то, что тот не предложил ему должность президента Берлинской академии.
Эти и многие другие поступки короля, вынудили Эйлера покинуть Берлин в 1766 г. В то время он получил выгодное предложение от Екатерины 2, которая недавно взошла на престол.
Возвращение в Санкт-Петербург
В Петербурге Леонарда Эйлера встретили с большими почестями. Ему сразу же предоставили престижный пост и были готовы выполнять практически любые его просьбы.
Хотя карьера Эйлера продолжала стремительно развиваться, его здоровье оставляло желать лучшего. Катаракта левого глаза, беспокоившая его еще в Берлине, все больше прогрессировала.
В результате, в 1771 г. Леонарду была сделана операция, которая привела к абсцессу и фактически полностью лишила зрения.
Через несколько месяцев в Петербурге произошел серьезный пожар, который затронул и жилище Эйлера. Фактически ослепшего ученого чудом удалось спасти Питеру Гримму – мастеровому из Базеля.
По личному распоряжению Екатерины 2, для Леонарда был построен новый дом.
Несмотря на многие испытания, Леонард Эйлер никогда не переставал заниматься наукой. Когда по состоянию здоровья он уже не мог писать, математику помогал его сын Иоганн Альбрехт.
Личная жизнь
В 1734 г. Эйлер взял в жены Катарину Гзель, дочь швейцарского живописца. В этом браке у пары родилось 13 детей, 8 из которых умерли еще в детстве.
Стоит заметить, что его первый сын, Иоганн Альбрехт, в будущем также стал талантливым математиком. В 20-летнем возрасте он оказался в составе Берлинской академии наук.
Второй сын, Карл, занимался изучением медицины, а третий, Кристоф, связал свою жизнь с военной деятельностью. Одна из дочерей Леонарда и Катарины, Шарлота, стала женой голландского аристократа, а другая, Хелена, вышла замуж за русского офицера.
После приобретения усадьбы в Шарлоттенбурге, Леонард привез туда овдовевшую мать, сестру и обеспечил жильем всех своих детей.
В 1773 г. Эйлер лишился любимой супруги. Через 3 года он вступил в брак с Саломеей-Абигайль. Интересен факт, что его избранница была сводной сестрой его покойной жены.
Смерть
Великий Леонард Эйлер умер 18 сентября 1783 г. в возрасте 76 лет. Причиной его кончины стал инсульт.
В день смерти ученого на его 2-х грифельных досках были обнаружены формулы, описывающие полет на воздушном шаре. В скором времени в Париже на шаре совершат свой полет братья Монгольфье.
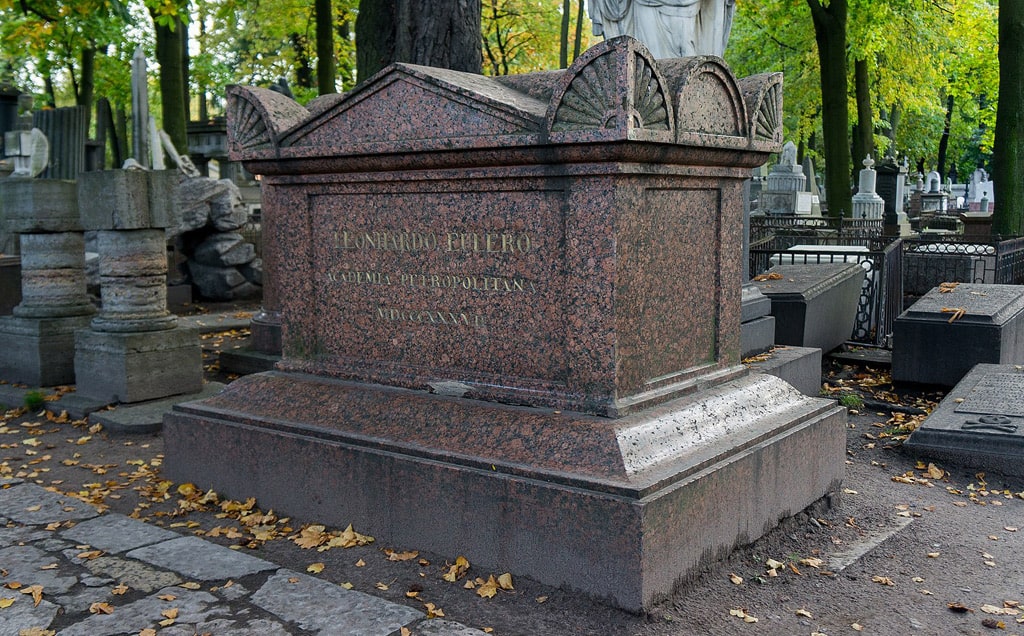
Вклад Эйлера в науку являлся настолько масштабным, что его статьи исследовались и печатались на протяжении еще 50 лет после кончины математика.
Научные открытия во время первого и второго пребывания в Санкт-Петербурге
В данный период биографии Леонард Эйлер глубоко изучал механику, теорию музыки и архитектуру. Он издал около 470 работ на самые разные темы.
Фундаментальный научный труд «Механика» затрагивал все области данной науки, включая небесную механику.
Ученый изучал природу звука, составив теорию удовольствия, вызываемого музыкой. При этом Эйлер присвоил интервалу тона, аккорду или их последовательности численные значения. Чем ниже была степень, тем выше оказывалось удовольствие.
Во второй части «Механики» Леонард уделил внимание судостроению и навигации.
Эйлер внес неоценимый вклад в развитие геометрии, картографии, статистики и теории вероятности. Отдельного внимания заслуживает 500-страничный труд «Алгебра». Интересен факт, что эту книгу он написал с помощью стенографиста.
Леонард глубоко исследовал теорию Луны, военно-морские науки, теорию чисел, натуральную философию и диоптрику.
Берлинские работы
Кроме 280 статей, Эйлер опубликовал множество научных трактатов. В период биографии 1744-1766 гг. он основал новый раздел математики – «вариационное исчисление».

Из-под его пера вышли трактаты по оптике, а также о траекториях планет и комет. Позже Леонард издал такие серьезные труды, как «Артиллерия», «Введение в анализ бесконечно малых», «Дифференциальное исчисление» и «Интегральное исчисление».
В течение всех лет, проведенных в Берлине, Эйлер исследовал оптику. В результате он стал автором трехтомной книги «Диоптрика». В ней он описывал разные способы усовершенствования оптических приборов, включая телескопы и микроскопы.
Система математических обозначений
Среди сотен наработок Эйлера наиболее заметной считается представление теории функций. Мало кому известен тот факт, что именно он первым ввел обозначение f(x) – функции «f» по аргументу «x».
Мужчина также вывел математические обозначения для тригонометрических функций в том виде, в каком они известны сегодня. Он стал автором символа «e», для образования натурального логарифма (известный как «число Эйлера»), а также греческую букву «Σ» для итоговой суммы и букву «i» для определения мнимой единицы.
Анализ
Леонард использовал показательные функции и логарифмы в аналитических доказательствах. Он изобрел метод, посредством которого удалось разлаживать логарифмические функции в степенной ряд.
Кроме этого, Эйлер применял логарифмы в работе с отрицательными и комплексными числами. В результате, он существенно расширил область использования логарифмов.
Затем ученый нашел уникальный способ решения квадратных уравнений. Он разработал новаторскую технику расчета интегралов, задействуя сложные пределы.
Кроме этого Эйлер вывел формулу вариационного исчисления, которая сегодня известна под названием – «уравнение Эйлера-Лагранжа».
Теория чисел
Леонард доказал малую теорему Ферма, тождества Ньютона, теорему Ферма о суммах 2-х квадратов, а также усовершенствовал доказательство теоремы Лагранжа о сумме 4-х квадратов.
Он также привнес важные дополнения в теорию совершенных чисел, которая волновала многих математиков того времени.
Физика и астрономия
Эйлер разработал способ решения уравнения «пучка Эйлера-Бернулли», которое затем начали активно использовать в инженерных вычислениях.
За свои заслуги в сфере астрономии Леонард удостоился многих престижных наград от Парижской академии. Он провел точные расчеты параллакса Солнца, а также с высокой точностью определил орбиты комет и прочих небесных тел.
Вычисления ученого помогли составить сверхточные таблицы небесных координат.
Леонард Эйлер
Фото Все
Видео Все
Эйлер. К 300-х летию ученого
Леонард Эйлер — биография
Леонард Эйлер – швейцарский ученый, внесший огромный вклад в развитие математики, физики, оптики, механики, астрономии и ряда прикладных наук. Член нескольких академий наук по всему миру.
Жизнь Леонарда Эйлера была полна удивительных открытий, принесших человечеству огромную пользу. Его масштабный вклад в развитие математики, механики, физики и астрономии невозможно переоценить, а его познания в самых разнообразных отраслях науки вызывают восхищение. За всю свою жизнь он издал более 850 трудов, в которых содержатся глубокие исследования ботаники, химии, медицины, древних языков. Имел членство во многих Академиях наук по всему миру.
Ранние годы
Леонард Эйлер родился 15 апреля 1707 года в городе Базель, Швейцария. Его родители – пастор Пауль Эйлер, друживший с математиком Бернулли, и Маргарита Эйлер, в девичестве Брукер. После рождения Леонарда семья перебралась в Рихен – селение неподалеку от Базеля. Здесь прошли первые годы жизни мальчика.
Образованием Эйлера-младшего занимался отец, который еще в раннем детстве обнаружил у сына математические способности. В возрасте 8 лет мальчик был отправлен на проживание к бабушке по линии матери и определен в базельскую гимназию.

Преподаватели заметили талант ученика, и в возрасте 13 лет ему позволили посещать занятия в университете Базеля. Леонард схватывал знания на лету, чем поразил профессора Иоганна Бернулли, брата Якоба Бернулли. Профессор дал подростку несколько математических работ выдающихся ученых и даже позволил посещать свой дом для разбора сложного материала.
Вскоре юноша успешно прошел экзаменационную комиссию на факультет искусств в университет Базеля. Уже через три года обучения получил ученую степень магистра, прочитав лекцию на латыни. В этом труде содержалось сравнение системы Рене Декарта с философией Исаака Ньютона.
Через некоторое время, стремясь порадовать отца-пастора, Леонард стал слушателем богословского факультета, но занятия математикой продолжал. Родитель шагом сына был растроган, но в дальнейшем, видя его талант к наукам, разрешил связать свою биографию с любимым делом.
В этот период Эйлер уже издал ряд научных трудов, таких как «Диссертация по физике о звуке». Это была конкурсная работа, по результатам которой комиссия решала вопрос о назначении на место профессора физики. Труд был оценен положительно, но все же профессорскую кафедру доверить 19-летнему Леонарду побоялись.
Однако, совсем скоро удача улыбнулась молодому ученому. Санкт-Петербургская академия наук, на тот момент находившаяся в стадии развития, испытывала необходимость в талантливых кадрах. Получив приглашение, Леонард Эйлер отправился в Северную столицу России.
Работа в Санкт-Петербурге
В 1727 году Эйлер поступил в адъюнктуру высшей математики петербургской академии наук. Российские власти поселили его в квартире и назначили жалованье в размере триста рублей в год. Потребовалось изучение русского языка, с чем математик справился в самый короткий срок.
Вскоре Леонард обрел друга – секретаря академии Кристиана Гольдбаха. Они вели научную переписку, которая в настоящее время представляет собой ценнейший источник знаний в научной истории 18 века.
Санкт-Петербургский период жизни ученого был весьма плодотворным. О его трудах узнал весь мир, а сам он стал уважаемым членом научного сообщества.
Покинуть Россию пришлось из-за политических причин – после кончины государыни Анны Иоанновны обстановка в стране была крайне нестабильной.
В 1741 году прусский монарх Фридрих II пригласил Эйлера для работы в новой академии наук, и ученый с семьей перебрался в Берлин.
Научная деятельность в Пруссии
Берлинская академия открылась в 1746 году, и Леонарда назначили руководителем отделения математических наук. Помимо этого, он был уполномочен заниматься кадровыми и финансовыми делами, следить за работой обсерватории.
С ростом авторитета Эйлера, росло и его благосостояние. Через несколько лет он смог позволить себе приобрести недвижимость в Шарлоттенбурге – просторное роскошное имение.
Отношения ученого с прусским монархом складывались далеко не гладко. Исследователи биографии Эйлера предполагают, что он затаил обиду на Фридриха II за то, что тот не назначил его президентом академии наук Берлина. Так это было или иначе, но в 1766 году Леонард покинул Берлин. К тому моменту он получил заманчивое предложение от новой российской императрицы Екатерины II.
Возвращение в Россию
Петербург встретил Эйлера с распростертыми объятиями. Сразу же по прибытию его назначили на высокий пост и выразили готовность предоставлять ему все необходимое.
В карьере ученого все шло благополучно, а вот со здоровьем дела обстояли иначе. Еще в Берлине у него обнаружили катаракту левого глаза, которая теперь начала прогрессировать. В 1771 году Леонард перенес операцию, в результате которой возник абсцесс и наступила почти полная слепота.
Спустя несколько месяцев в одном из домов Санкт-Петербурга случился пожар, пламя которого перекинулось и на квартиру Леонарда. Почти потерявшего зрение ученого вынес из огня базельский мальчик-портной, выполнявший функции секретаря.
После происшествия императрица Екатерина II лично распорядилась отстроить для светила науки новое жилище.
Какие бы испытания не выпадали на долю Эйлера, он не оставлял свои научные изыскания. Когда его глаза практически ослепли, читал и записывал для него сын Иоганн Альбрехт.
Открытия в России
Научная деятельность Эйлера в Санкт-Петербурге была направлена на глубокое изучение механики, архитектуры и теории музыки. Здесь он опубликовал порядка 470 трудов в самых разнообразных областях.
Масштабная работа «Механика» — глубокое исследование данной науки, в том числе небесной механики.
Леонард разобрал природу звуков и составил собственную «теорию удовольствия», объясняющую чувства человека, вызванные прослушиванием музыки. Эйлер систематизировал тона, интервалы и аккорды, присвоив им численные значения.
Вторая часть «Механики» освещала судостроение и навигацию.
Вклад ученого в изучение и развитие таких наук, как статистика, геометрия и картография невозможно переоценить. Особое место занимает научный труд «Алгебра», для записи пятисот страниц которого был привлечен стенографист.
Объектами его исследований были теория Луны, диоптрика, теория чисел, натуральная философия и различные прикладные науки.
Научные достижения в берлинский период
В Пруссии ученый опубликовал 280 статей и множество ценных научных трактатов. Он стал основателем нового раздела математики – «вариационного исчисления».
Эйлер стал автором гениальных трактатов по оптике и о траекториях движения небесных тел. В Берлине родились его труды «Интегральное исчисление», «Введение в анализ бесконечно малых», «Дифференциальное исчисление» и «Артиллерия».
Годы работы Леонарда в Пруссии подарили научному миру трехтомный труд «Диоптрика», в котором излагались методы усовершенствования микроскопов, телескопов и других оптических приборов.
Создание системы обозначений в математике
Одним из важнейших достижений Леонарда является систематизация теории функций. Именно его наработками сегодня пользуется весь мир, решая тригонометрические функции. Его авторству принадлежит символ «е», служащий для образования логарифмов и известный в настоящее время, как «число Эйлера». Он придумал использовать греческую букву «Σ» для подведения итоговой суммы и символ «i», определяющий мнимую единицу.
Геометрия
Исследуя элементарную геометрию, Эйлер сделал несколько открытий, касаемых треугольников, не обнаруженных древнегреческим математиком Евклидом.
В 1760-м он опубликовал масштабную работу «Исследования о кривизне поверхностей», где рассчитал формулу связи главной кривизны и кривизны сечения поверхности.
Еще через 10 лет ученый издал труд «О телах, поверхность которых можно развернуть на плоскость».
Теория чисел
Эйлер блестяще доказал тождество Ньютона, малую теорему Ферма и его же теорему о сумме двух квадратов. Кроме того, им была усовершенствована теорема о сумме 4-х квадратов француза Лагранжа.
Леонард стал автором дополнений к теории совершенных чисел, так волновавшую ученых тех лет.
Наука о звездах и физика
Эйлер разобрался с «пучком Эйлера-Бернулли», дав возможность инженерам использовать это решение в своих вычислениях.
Вклад в развитие астрономии принес ученому множество высоких наград, учрежденных парижской научной академией. Он предоставил ряд точных расчетов такого явления, как параллакс Солнца, и что не менее важно – максимально точно рассчитал орбиты небесных тел.
На основе вычислений Леонарда была составлена таблица координат планет, комет и других небесных объектов.
Личная жизнь
Первой супругой математика стала Катарина Гзель, дочь художника из Швейцарии. Они поженились в 1734 году и родили 13 детей, восемь из которых не дожили до совершеннолетия.
Первенец – Иоганн Альбрехт, пошел по стопам родителя и стал выдающимся математиком. В возрасте 20 лет он удостоился чести стать членом академии наук в Пруссии.

Карл, второй сын, углубленно изучал медицину, а третий ребенок, Кристоф посвятил себя военной службе.
Дочь Шарлотта вышла замуж за голландского аристократа, а Хелена связала свою личную жизнь с русским военным.
Купив имение в Шарлоттенбурге, Эйлер поселил там пожилую мать и сестру, всем остальным членам семьи также приобрел недвижимость.
Катарина скончалась в 1773 году, и через три года ученый вновь вступил в брак. Его избранницей стала Саломея-Абигайль, сводная сестра покойной супруги.
Смерть
Гениальный Леонард Эйлер скончался 18 сентября 1783 года от инсульта. Он прожил насыщенную, яркую жизнь длиною в 76 лет.
После его смерти в доме были обнаружены грифельные доски, испещренные формулами расчета полета воздушного шара. Вскоре в небо Парижа взмыл легендарный шар с братьями Монгольфье.

Эйлер внес в науку настолько фундаментальный вклад, что его труды изучались и публиковались еще целых полвека после его кончины.
Научные дискуссии
Эйлер охотно вступал в научные дискуссии, наиболее известными из которых стали:
Во всех упомянутых дискуссиях современное научное сообщество поддерживает позицию Леонарда Эйлера.
Библиография
Ccылки
Эйлер, Леонард
| Леонард Эйлер | ||||||||
| Leonhard Euler | ||||||||
 Портрет, выполненный Эмануэлем Хандманном (1756) | ||||||||
| Дата рождения: | ||||||||
|---|---|---|---|---|---|---|---|---|
 | Того ради нахожусь принужден, как ради слабого здоровья, так и других обстоятельств, искать приятнейшего климата и принять от его Королевского Величества Прусского учиненное мне призывание. Того ради прошу Императорскую Академию наук всеподданнейше меня милостиво уволить и снабдить для моего и домашних моих проезду потребным пашпортом [6] |  |
 | Все сии диссертации не токмо хороши, но и весьма превосходны, ибо он [Ломоносов] пишет о материях физических и химических весьма нужных, которые по ныне не знали и истолковать не могли самые остроумные люди, что он учинил с таким успехом, что я совершенно уверен в справедливости его изъяснений. При сём случае г. Ломоносову должен отдать справедливость, что имеет превосходное дарование для изъяснения физических и химических явлений. Желать должно, чтоб и другия Академии в состоянии были произвести такия откровения, как показал г. Ломоносов. В июне 1741 года Леонард Эйлер с женой, двумя сыновьями и четырьмя племянниками прибыл в Берлин. Он провёл там 25 лет и издал около 260 работ. В 1753 году Эйлер купил поместье в Шарлоттенбурге (пригород Берлина) с садом и участком. Мать известила Эйлера о смерти в Швейцарии его отца; вскоре она переехала к Эйлеру. По отзывам современников, Эйлер всю жизнь оставался скромным, жизнерадостным, чрезвычайно отзывчивым человеком, всегда готовым помочь другому. Однако отношения с королём не складываются: Фридрих находит нового математика невыносимо скучным, совершенно не светским, и обращается с ним пренебрежительно. В 1759 году умер Мопертюи, президент Берлинской Академии наук. Пост президента Академии король Фридрих II предложил Даламберу, но тот отказался. Фридрих, недолюбливавший Эйлера, всё же поручил ему руководство Академией, однако без титула президента. 1765: новый шедевр Эйлера, «Теория движения твёрдых тел». В 1766 году опубликованы «Элементы вариационного исчисления». Именно здесь впервые появилось название нового раздела математики, созданного Эйлером и Лагранжем. В 1762 году на русский престол вступила Екатерина II, которая осуществляла политику просвещённого абсолютизма. Хорошо понимая значение науки как для прогресса государства, так и для собственного престижа, она провела ряд важных, благоприятных для науки преобразований в системе народного просвещения и культуры. Императрица предложила Эйлеру управление математическим классом, звание конференц-секретаря Академии и оклад 1800 рублей в год. «А если не понравится, — говорилось в письме её представителю, — благоволит сообщить свои условия, лишь бы не медлил приездом в Петербург». Эйлер сообщил в ответ свои условия: Все эти условия были приняты. В письме от 6 января 1766 года Екатерина пишет канцлеру графу Воронцову:
Эйлер подал королю прошение об увольнении со службы, но никакого ответа не получил. Подал повторно — но Фридрих не желал даже обсуждать вопрос о его отъезде. В ответ на это Эйлер прекратил работать для Берлинской Академии. Эйлер возвращается в Россию, теперь уже навсегда. Снова Россия (1766—1783)В июле 1766 года 60-летний Эйлер, его семья и домочадцы (всего 18 человек) прибыли в российскую столицу. Сразу же по прибытии он был принят императрицей. Екатерина, теперь уже Вторая, встретила его как августейшую особу и осыпала милостями: пожаловала 8000 рублей на покупку дома на Васильевском острове и на приобретение обстановки, предоставила на первое время одного из своих поваров и поручила подготовить соображения о реорганизации Академии. К несчастью, после возвращения в Петербург у Эйлера образовалась катаракта левого глаза — он перестал видеть. Вероятно, по этой причине обещанный пост вице-президента Академии он так и не получил. Однако слепота не отразилась на его работоспособности. Эйлер диктовал свои труды мальчику-портному, который всё записывал по-немецки. Число опубликованных им работ даже возросло; за полтора десятка лет второго пребывания в России он продиктовал более 400 статей и 10 книг. 1767—1770: работа над двухтомной классической монографией «Универсальная арифметика» (издавалась также под названиями «Начала алгебры» и «Полный курс алгебры»). На русском языке этот замечательный труд выходит сразу же (первый том: 1768), на немецком — два года спустя. Книга была переведена на многие языки и переиздавалась около 30 раз (трижды — на русском). Все последующие учебники алгебры создавались под сильнейшим влиянием книги Эйлера. В 1771 году в жизни Эйлера произошли два серьёзных события. В мае в Петербурге случился большой пожар, уничтоживший сотни зданий, в том числе дом и почти всё имущество Эйлера. Самого учёного с трудом спасли. Все рукописи удалось уберечь от огня; сгорела лишь часть «Новой теории движения луны», но она быстро была восстановлена с помощью самого Эйлера, сохранившего до глубокой старости феноменальную память. Эйлеру пришлось временно переселиться в другой дом. В сентябре того же года, по особому приглашению императрицы, в Санкт-Петербург прибыл для лечения Эйлера известный немецкий окулист барон Вентцель. После осмотра он согласился сделать Эйлеру операцию и удалил с левого глаза катаракту. Эйлер снова стал видеть. Врач предписал беречь глаз от яркого света, не писать, не читать — лишь постепенно привыкать к новому состоянию. Однако уже через несколько дней после операции Эйлер снял повязку, и вскоре потерял зрение снова. На этот раз — окончательно. 1772: «Новая теория движения Луны». Эйлер наконец завершил свой многолетний труд, приближённо решив задачу трёх тел. В 1773 году по рекомендации Даниила Бернулли в Петербург приехал из Базеля ученик Бернулли, Никлаус Фусс. Это было большой удачей для Эйлера. Фусс обладал редким сочетанием математического таланта и умения вести практические дела, что и дало ему возможность сразу же после приезда взять на себя заботы о математических трудах Эйлера. Вскоре Фусс женился на внучке Эйлера. В последующие десять лет — до самой своей смерти — Эйлер преимущественно ему диктовал свои труды, хотя иногда пользовался «глазами старшего сына» и других своих учеников. 1779: выходит «Всеобщая сферическая тригонометрия», первое полное изложение всей системы сферической тригонометрии. Эйлер активно трудился до последних дней. В сентябре 1783 года 76-летний учёный стал ощущать головные боли и слабость. 7 (18) сентября после обеда, проведённого в кругу семьи, беседуя с академиком А. И. Лекселем о недавно открытой планете Уран и её орбите, он внезапно почувствовал себя плохо. Эйлер успел произнести: «Я умираю», — и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг. «Он перестал вычислять и жить», — сказал Кондорсе на траурном заседании Парижской Академии наук (фр. Il cessa de calculer et de vivre ). Его похоронили на Смоленском лютеранском кладбище в Петербурге. Надпись на памятнике гласила: «Здесь покоятся бренные останки мудрого, справедливого, знаменитого Леонарда Эйлера». В 1955 году прах великого математика был перенесён в «Некрополь XVIII века» на Лазаревском кладбище Александро-Невской лавры. Плохо сохранившийся надгробный памятник при этом заменили. Интересные фактыОценкиАкадемик С. И. Вавилов писал: «Вместе с Петром I и Ломоносовым, Эйлер стал добрым гением нашей Академии, определившим её славу, её крепость, её продуктивность». Адреса в Санкт-ПетербургеВклад в наукуЭйлер оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. С точки зрения математики, XVIII век — это век Эйлера. Если до него достижения в области математики были разрозненны и не всегда согласованны, то Эйлер впервые увязал анализ, алгебру, тригонометрию, теорию чисел и др. дисциплины в единую систему, и добавил немало собственных открытий. Значительная часть математики преподаётся с тех пор «по Эйлеру». Благодаря Эйлеру в математику вошли общая теория рядов, удивительная по красоте «формула Эйлера», операция сравнения по целому модулю, полная теория непрерывных дробей, аналитический фундамент механики, многочисленные приёмы интегрирования и решения дифференциальных уравнений, число e, обозначение i для мнимой единицы, гамма-функция с её окружением и многое другое. По существу, именно он создал несколько новых математических дисциплин — теорию чисел, вариационное исчисление, теорию комплексных функций, дифференциальную геометрию поверхностей, специальные функции. Другие области его трудов: диофантов анализ, астрономия, оптика, акустика, статистика и т. д. Познания Эйлера были энциклопедичны; кроме математики, он глубоко изучал ботанику, медицину, химию, теорию музыки, множество европейских и древних языков. Эйлер охотно участвовал в научных дискуссиях, из которых наибольшую известность получили [19] : Во всех упомянутых случаях Эйлер отстаивал правильную позицию. Теория чиселП. Л. Чебышёв писал: «Эйлером было положено начало всех изысканий, составляющих общую теорию чисел». Большинство математиков XVIII века занимались развитием анализа, но Эйлер пронёс увлечение древней арифметикой через всю свою жизнь. Благодаря его трудам интерес к теории чисел к концу века возродился. Эйлер продолжил исследования Ферма, ранее высказавшего (под влиянием Диофанта) ряд разрозненных гипотез о натуральных числах. Эйлер строго доказал эти гипотезы, значительно обобщил их и объединил в содержательную теорию чисел. Он ввёл в математику исключительно важную «функцию Эйлера» и сформулировал с её помощью «теорему Эйлера». Эйлер создал теорию сравнений и квадратичных вычетов, указав для последних критерий Эйлера. Он опроверг гипотезу Ферма о том, что все числа вида Доказал утверждение Ферма о представлении нечётного простого числа в виде суммы двух квадратов. Ввел дзета-функцию, обобщение которой получило впоследствии имя Римана: где где произведение берётся по всем простым числам Эйлер доказал Великую теорему Ферма для В задаче о количестве разбиений натурального числа Он открыл, что в теории чисел возможно применение методов математического анализа, положив начало аналитической теории чисел. В основе её лежат тождество Эйлера и общий метод производящих функций. Эйлер ввёл понятие первообразного корня и выдвинул гипотезу, что для любого простого числа p существует первообразный корень по модулю p; доказать это он не сумел, позднее теорему доказали Лежандр и Гаусс. Большое значение в теории имела другая гипотеза Эйлера — квадратичный закон взаимности, также доказанный Гауссом. Математический анализОдна из главных заслуг Эйлера перед наукой — монография «Введение в анализ бесконечно малых» (1748). В 1755 году выходит дополненное «Дифференциальное исчисление», а в 1768—1770 годах — три тома «Интегрального исчисления». В совокупности это фундаментальный, хорошо иллюстрированный примерами курс, с продуманной терминологией и символикой, откуда многое перешло и в современные учебники. Собственно современные методы дифференцирования и интегрирования были опубликованы в данных трудах. Основание натуральных логарифмов было известно ещё со времён Непера и Якоба Бернулли, однако Эйлер выполнил настолько глубокое исследование этой важнейшей константы, что с тех пор она носит его имя. Другая исследованная им константа: постоянная Эйлера — Маскерони. Он делит с Лагранжем честь открытия вариационного исчисления, выписав уравнения Эйлера — Лагранжа для общей вариационной задачи. В 1744 году Эйлер опубликовал первую книгу по вариационному исчислению («Метод нахождения кривых, обладающих свойствами максимума либо минимума»). Эйлер значительно продвинул теорию рядов и распространил её на комплексную область, получив при этом знаменитую формулу Эйлера. Большое впечатление на математический мир произвели ряды, впервые просуммированные Эйлером, в том числе не поддававшийся до него никому ряд обратных квадратов: Он первый дал систематическую теорию интегрирования и используемых там технических приёмов, нашёл важные классы интегрируемых дифференциальных уравнений. Он открыл эйлеровы интегралы — ценные классы специальных функций, возникающие при интегрировании: бета-функция и гамма-функция Эйлера. Одновременно с Клеро вывел условия интегрируемости линейных дифференциальных форм от двух или трёх переменных (1739). Первый ввёл двойные интегралы. Получил серьёзные результаты в теории эллиптических функций, в том числе первые теоремы сложения. ГеометрияВ элементарной геометрии Эйлер обнаружил несколько фактов, не замеченных Евклидом: Второй том «Введения в анализ бесконечно малых» (1748) — это первый в мире учебник по аналитической геометрии и основам дифференциальной геометрии. Термин аффинные преобразования впервые введён в этой книге вместе с теорией таких преобразований. В 1760 году вышли фундаментальные «Исследования о кривизне поверхностей». Эйлер обнаружил, что в каждой точке гладкой поверхности имеются два нормальных сечения с минимальным и максимальным радиусами кривизны, и плоскости их взаимно перпендикулярны. Вывел формулу связи кривизны сечения поверхности с главными кривизнами. 1771 год: опубликовано сочинение «О телах, поверхность которых можно развернуть на плоскость». В этой работе введено понятие развёртывающейся поверхности, то есть поверхности, которая может быть наложена на плоскость без складок и разрывов. Эйлер, однако, даёт здесь вполне общую теорию метрики, от которой зависит вся внутренняя геометрия поверхности. Позже исследование метрики становится у него основным инструментом теории поверхностей. КомбинаторикаЭйлер много внимания уделял представлению натуральных чисел в виде сумм специального вида и сформулировал ряд теорем для вычисления числа разбиений. Он исследовал алгоритмы построения магических квадратов методом обхода шахматным конём. При решении комбинаторных задач он глубоко изучил свойства сочетаний и перестановок, ввёл в рассмотрение числа Эйлера. Другие области математикиМеханика и математическая физикаМножество работ Эйлера посвящены математической физике: механике, гидродинамике, акустике и др. В 1736 году вышел трактат «Механика, или наука о движении, в аналитическом изложении», знаменующий новый этап в развитии этой древней науки. 29-летний Эйлер отказался от традиционного геометрического подхода к механике и подвёл под неё строгий аналитический фундамент. По существу, с этого момента механика становится прикладной математической дисциплиной. В 1755 году публикуются «Общие принципы движения жидкостей», в которых положено начало теоретической гидродинамике. Выведены основные уравнения гидродинамики (уравнение Эйлера) для жидкости без вязкости. Разобраны решения системы для разных частных случаев. В 1765 году в книге «Теория движения твёрдых тел» Эйлер математически описал кинематику твёрдого тела конечных размеров (до него исследовалось в основном движение точки). Он ввёл в математику углы Эйлера и теорему вращения. Его имя также носят кинематическая формула распределения скоростей в твёрдом теле, уравнения (Эйлера — Пуассона) динамики твёрдого тела, важный случай интегрируемости в динамике твёрдого тела. Эйлер обобщил принцип наименьшего действия, довольно путано изложенный Мопертюи, и указал на его основополагающее значение в механике. К сожалению, он не раскрыл вариационный характер этого принципа, но всё же привлёк к нему внимание физиков, которые позднее выяснили его фундаментальную роль в природе. АстрономияЭйлер много работал в области небесной механики. Он заложил основу теории возмущений, позднее завершённой Лапласом, и разработал очень точную теорию движения Луны. Эта теория оказалась пригодной для решения насущной задачи определения долготы на море, и английское Адмиралтейство выплатило за неё Эйлеру специальную премию. Основные труды Эйлера в этой области: Инженерное делоВ 1757 году Эйлер впервые в истории нашёл формулы для определения критической нагрузки при сжатии упругого стержня. Однако в те годы эти формулы не могли найти практического применения. Почти сто лет спустя, когда во многих странах — и прежде всего в Англии — стали строить железные дороги, потребовалось рассчитать прочность железнодорожных мостов. Модель Эйлера принесла практическую пользу в проведении экспериментов. ПамятьВ честь Эйлера названы: Полное собрание сочинений Эйлера, издаваемое с 1909 года Швейцарским обществом естествоиспытателей, до сих пор не завершено; планировался выпуск 75 томов, из них вышло 73 [22] : Восемь дополнительных томов будут посвящены научной переписке Эйлера (свыше 3000 писем [23] ). В 1907 году российские и многие другие учёные отметили 200-летие великого математика. Марки, монеты, банкнотыВ 2007 году Центробанк РФ выпустил памятную монету [C 9] в ознаменование 300-летия со дня рождения Л. Эйлера. Портрет Эйлера помещался также на швейцарскую 10-франковую банкноту (6-я серия) и на почтовые марки Швейцарии, России и Германии.
|























 — простые; оказалось, что
— простые; оказалось, что  делится на 641.
делится на 641.
 вещественно. Эйлер вывел для неё разложение:
вещественно. Эйлер вывел для неё разложение: ,
, . Благодаря этому он доказал, что сумма ряда обратных простых
. Благодаря этому он доказал, что сумма ряда обратных простых  расходится.
расходится. и
и  , создал полную теорию непрерывных дробей, исследовал различные классы диофантовых уравнений, теорию разбиений чисел на слагаемые.
, создал полную теорию непрерывных дробей, исследовал различные классы диофантовых уравнений, теорию разбиений чисел на слагаемые. получил формулу, выражающую производящую функцию числа разбиений
получил формулу, выражающую производящую функцию числа разбиений  через бесконечное произведение
через бесконечное произведение