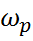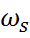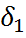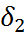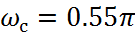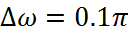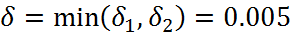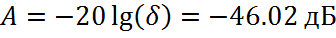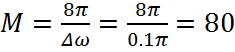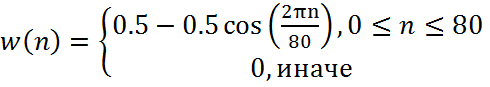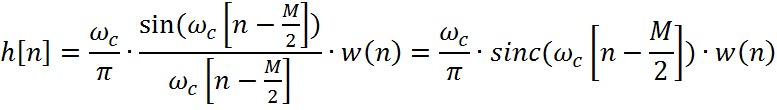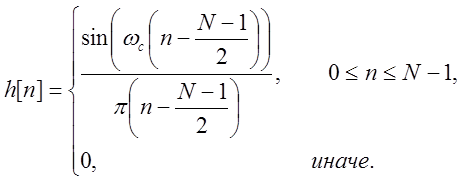что произойдет с окном кайзера с увеличением параметра сглаживания бета при фиксированной длине окна
Функции оконного сглаживания
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
В предыдущем разделе мы анализировали эффект растекания спектра дискретного преобразования Фурье (ДПФ) и говорили, что он возникает в результате дискретизации дискретно-временного преобразования Фурье (ДВПФ) ограниченного во времени сигнала.
Таким образом, ДВПФ комплексного гармонического сигнала полностью описывается ДВПФ оконной функции, которая используется для ограничения длительности сигнала.
В предыдущем разделе мы рассмотрели эффект растекания ДПФ, который возникает, когда частота гармонического сигнала не совпадает с частотами дискретизации ДВПФ. Мы отмечали, что эффект растекания спектра приводит к гребешковым искажениям амплитуды гармонического сигнала, а также к уменьшению динамического диапазона спектрального анализа ввиду маскирования слабых сигналов под боковыми лепестками мощных гармоник при растекании спектра последних.
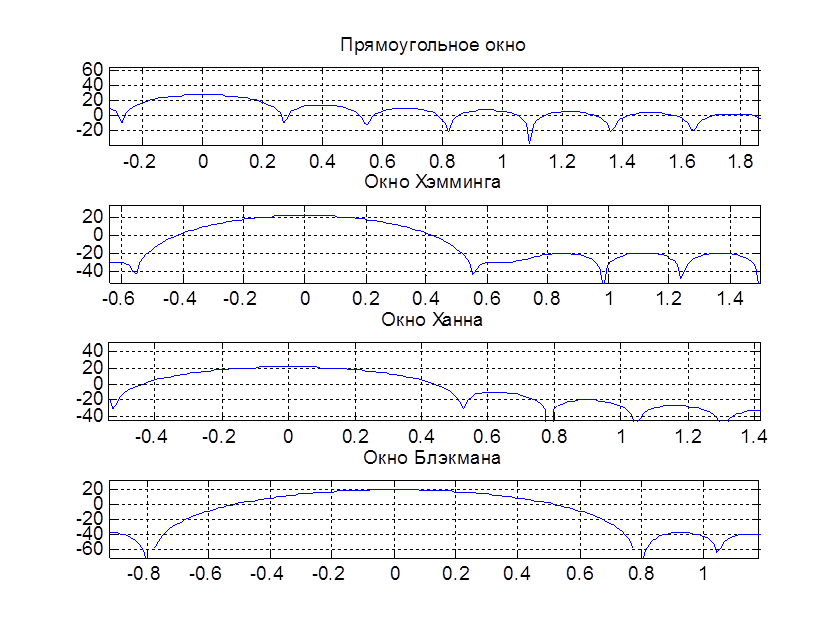
Можно видеть, что уровень боковых лепестков спектра окна Хемминга значительно ниже чем у прямоугольного окна. Таким образом, использовав сглаженные окна, можно получить увеличение динамического диапазона спектрального анализа, и также уменьшить уровень гребешковых искажений.
Если для вывода спектра на график необходимо разместить в центре, то можно представить частоту от до и произвести перестановку спектральных компонент, как это показано на рисунке 2б.
Можно многими способами сгладить прямоугольное окно, и таким образом, получить множество семейств различных оконных функций. Поэтому нам надо рассмотреть параметры оконных функций, которые так или иначе влияют на качество спектрального анализа. Имея набор параметров мы сможем сравнить окна между собой и получить объективный подход для выбора того или иного окна для практического применения.
Еще раз заметим, что когерентное усиление относится только к случаю, когда частота гармонического сигнала попадает на бин ДПФ и эффекта растекания не наблюдается.
Для исключения зависимости от длины выборки можно нормировать уровень гребешковых искажений к уровню когерентного усиления. Тогда
На рисунке 3 показаны частотные параметры спектральной плотности энергии оконных функций.
Значение частоты на рисунке 3 приведено в единицах спектральных отсчетов ДПФ (бин ДПФ).
На графиках можно видеть значение когерентного усиления (в данном случае усиление не нормировано к значению усиления прямоугольного окна). Относительно можно выделить уровень максимального бокового лепестка оконной функции.
Тогда можно заключить, что
Поскольку эквивалентная шумовая полоса сглаженных окон выше чем прямоугольного окна, то это означает более высокий уровень шума на выходе.
Это можно пояснить так. Поскольку прямоугольное окно обладает максимальным когерентным усилением и является согласованным фильтром для гармонического сигнала на частоте бина ДПФ, то оно обеспечивает максимальное отношение сигнал–шум на выходе. Любое другое сглаженное окно будет обеспечивать худшее отношение сигнал–шум для гармонического сигнала на частоте бина ДПФ.
Заметим, что при построении графиков, разница в когерентном усилении оконных функций была скомпенсирована и выровнена с усилением прямоугольного окна. В результате значение гармоник на частоте 100 Гц для всех окон равно 20 дБ.
Можно видеть, что прямоугольное окно обеспечивает максимальное отношение сигнал–шум дБ для сигнала на частоте 100 Гц, но при этом наблюдаются максимальные гребешковые искажения дБ.
При использовании окна Хемминга величина гребешковых искажений уменьшилась до значения дБ, однако отношение сигнал–шум также ухудшилось на величину дБ.
Для окна Блэкмана-Харриса гребешковые искажения составляют дБ, в то время как отношение сигнал–шум ухудшается на величину дБ.
Данный пример был рассчитан с использованием библиотеки DSPL–2.0. Исходный код программы scalloping_loss.c расчета данных для построения графиков рисунка 5 приведён в следующем листинге.
Оконные функции используются в различных задачах спектрального анализа, а также при синтезе цифровых КИХ-фильтров. В задачах спектрального анализа мы стремимся получить более узкий основной лепесток спектра оконной функции, в то время как в задачах синтеза КИХ-фильтров часто требуется обеспечить линейность ФЧХ, что требует симметрии оконной функции во временно́й области.
Для удовлетворения требований спектрального анализа и задач синтеза линейнофазовых КИХ-фильтров различают периодические и симметричные оконные функции. Периодические оконные функции обладают лучшими частотными свойствами, но не имеют свойства временно́й симметрии. Пример периодических и симметричных треугольных окон Бартлетта показан на рисунке 6 для четной и нечетной длин окна.
Красным цветом показан один период оконной функции при расчете ДПФ, синим — периодические повторения, которые возникают при дискретизации ДВПФ оконной функции.
Прямоугольное окно имеет единичные значения для всех :
Документация
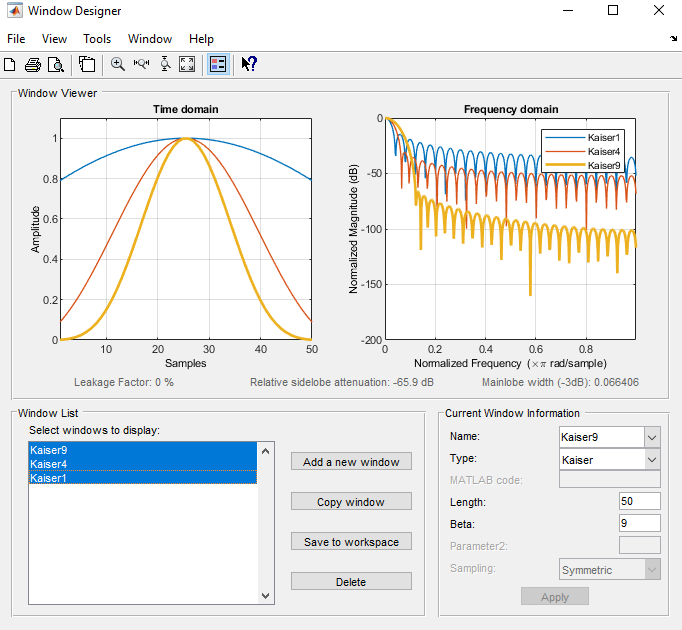
Окно Кайзера
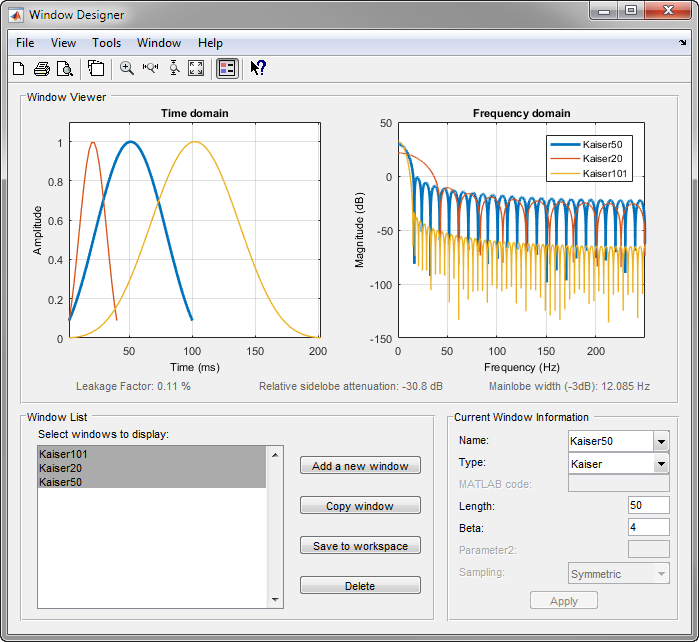
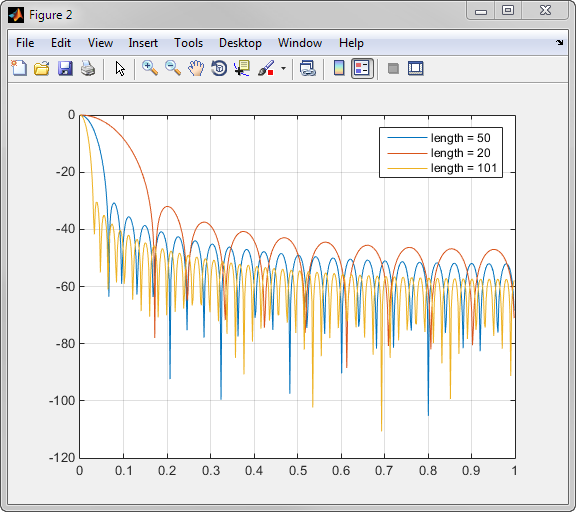
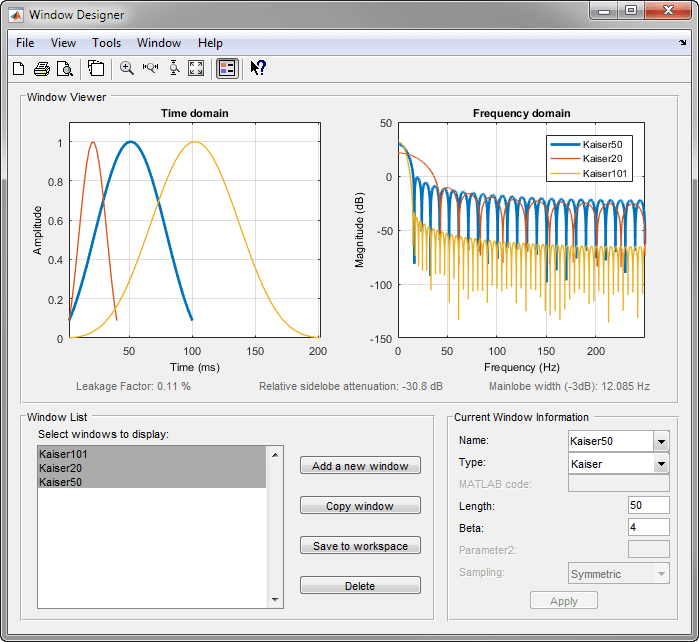
Когда β увеличивается, относительные уменьшения затухания бокового лепестка и mainlobe увеличения ширины. Этот снимок экрана показывает, как относительное затухание бокового лепестка приблизительно остается таким же для фиксированного параметра β, когда длина варьируется.
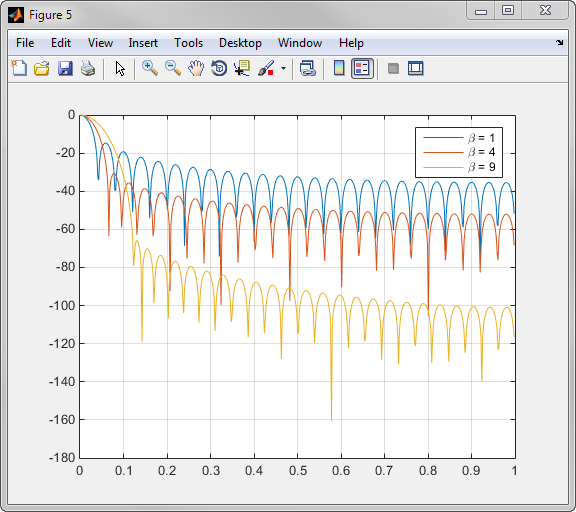
Примеры окон Кайзера с длиной 50 и параметры β 1, 4, и 9 показывают в этом примере.
Чтобы создать эти окна Кайзера с помощью командной строки MATLAB, введите следующее:
Окна Кайзера в КИХ-проекте
Существует две формулы проекта, которые могут помочь вам спроектировать КИХ-фильтры, чтобы соответствовать набору спецификаций фильтра с помощью окна Кайзера. Достигнуть относительного затухания бокового лепестка –α дБ, β ( beta ) параметр
Для ширины перехода Δ ω рад/выборка, используйте длину
Спроектированное использование фильтров этой эвристики будет соответствовать спецификациям приблизительно, но необходимо проверить это. Спроектировать фильтр lowpass с частотой среза 0.5 π рад/выборка, ширина перехода 0.2 π рад/выборка, и 40 дБ затухания в полосе задерживания, пробует
kaiserord функционируйте оценивает порядка фильтра, частоту среза, и бета параметр окна Кайзера должен был соответствовать данному набору спецификаций частотного диапазона.
Пульсация в полосе пропускания является примерно тем же самым как пульсацией в полосе задерживания. Как вы видите из частотной характеристики, этот фильтр почти соответствует спецификациям:
Смотрите также
Приложения
Функции
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Документация Signal Processing Toolbox
Поддержка
© 1994-2020 The MathWorks, Inc.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.
6. Определение ширины главного лепестка и относительного уровня боковых лепестков амплитудных спектров окон
Рис. 7. Масштабированные АЧХ окон в логарифмическом масштабе
Ширина главного лепестка
Относительный уровень боковых лепестков, дБ
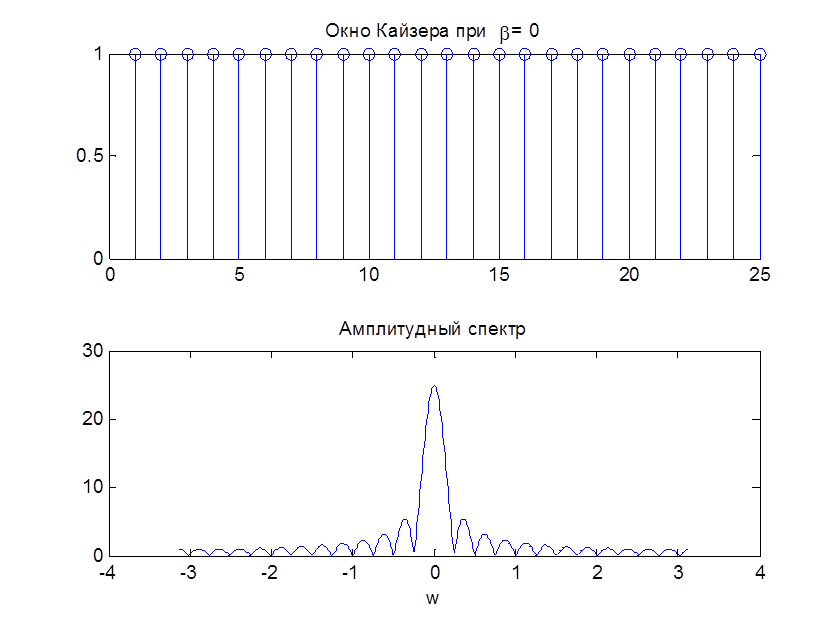
7. Построение графиков окна Кайзера и его АЧХ для N=25 и разных β
С помощью следующего кода MATLAB выполним построение графиков окна Кайзера и АЧХ этих окон для N=25, β=0, 1, 5.
figure(1), subplot(211), stem(k1)
title (‘Окно Кайзера при \beta= 0’)
title (‘Амплитудный спектр’), xlabel(‘w’);
figure(2), subplot(211), stem(k2)
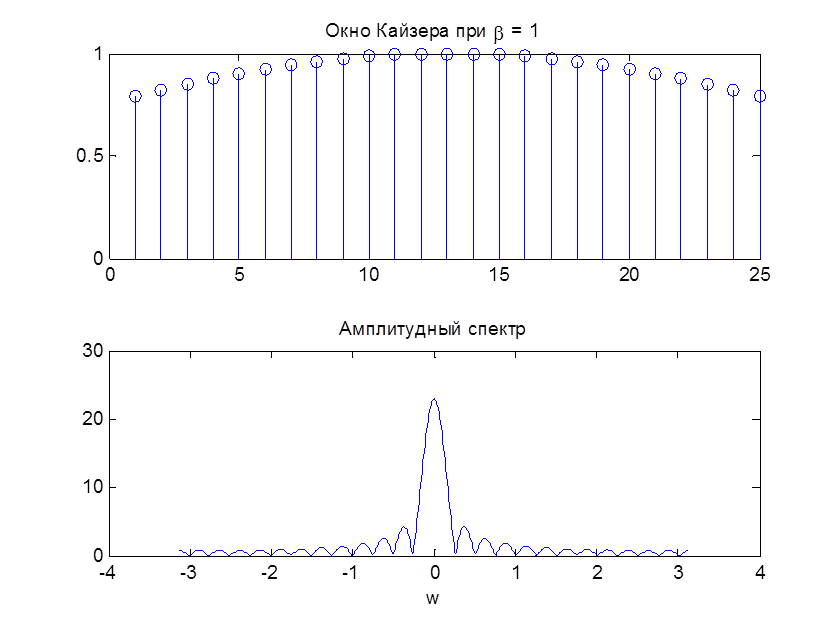
title (‘Окно Кайзера при \beta = 1’)
title (‘Амплитудный спектр’), xlabel(‘w’);
figure(3), subplot(211), stem(k3)
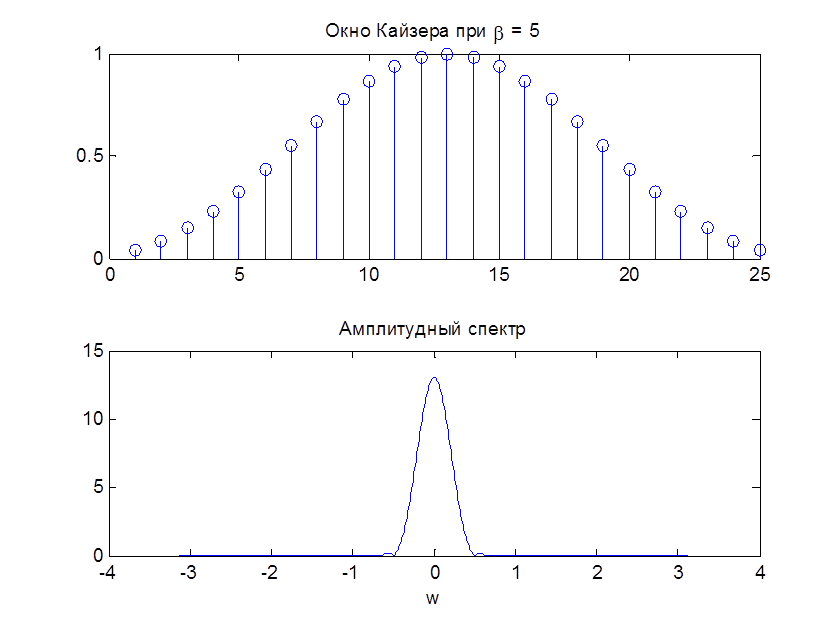
title (‘Окно Кайзера при \beta = 5’)
title (‘Амплитудный спектр’), xlabel(‘w’);
Рис. 8. Окно Кайзера и его АЧХ при N=25, β=0
Рис. 9. Окно Кайзера и его АЧХ при N=25, β=1
Рис. 10. Окно Кайзера и его АЧХ при N=25, β=5
Ширина главного лепестка
Относительный уровень боковых лепестков, дБ
При увеличении параметра β окно спадает к нулю более плавно. Чем больше бета, тем большая энергия приходится на главный лепесток (главный лепесток шире) и тем меньше уровень боковых лепестков.
Из этого следует, что уменьшаются пульсации в полосе задерживания фильтра, но одновременно с этим увеличивается ширина переходной полосы (главный лепесток становится шире)
8. Синтез фильтра по заданным условиям
Произведем расчет фильтра, удовлетворяющего данным условиям:
1. Нормированные граничные частоты полосы пропускания и полосы задерживания составляют 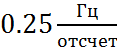
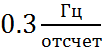
Частота среза фильтра 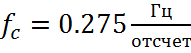
Ширина переходной полосы фильтра 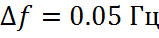
2. Допустимый уровень пульсаций
В децибелах
Такому уровню соответствует окно Ханна (A=-44 дБ)
3. Определим порядок фильтра:
4. Окно Ханна фильтра:
5. Импульсная характеристика фильтра:
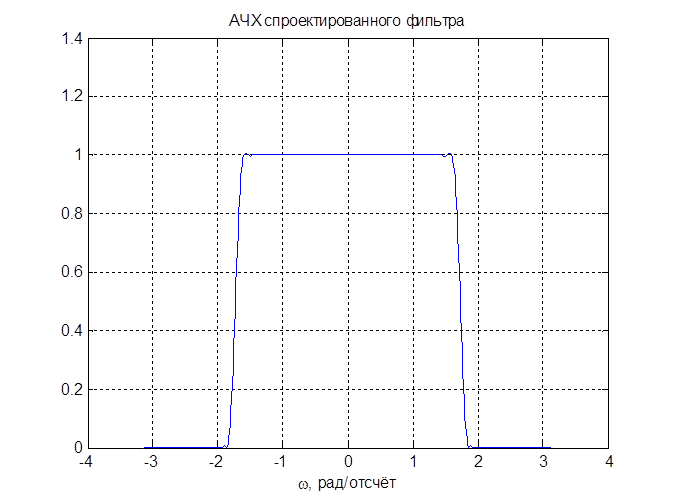
С помощью MATLAB построим график АЧХ фильтра:
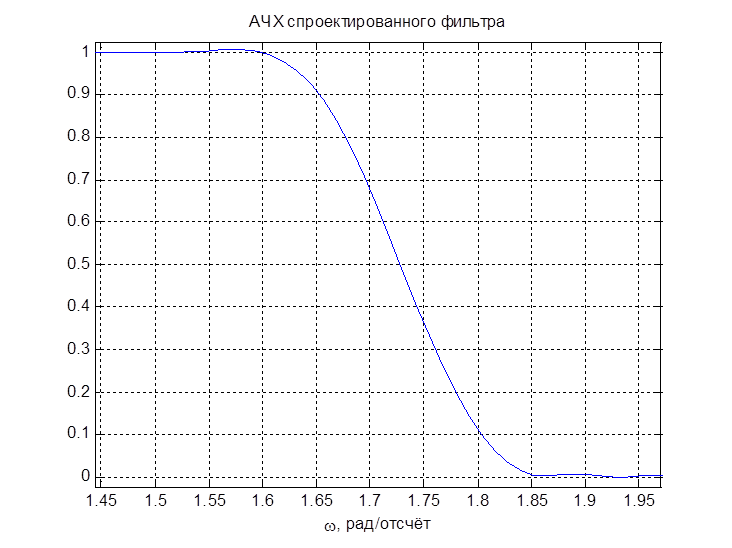
Рис. 11. АЧХ спроектированного фильтра
Рис. 12. Увеличенный фрагмент АЧХ
По увеличенному фрагменту на рис. 12 видно, что 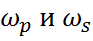
9. Фильтрация сигнала спроектированным фильтром
С помощью следующего кода MATLAB проведем фильтрацию сигнала nspeech2 фильтром, спроектированным в пункте 8
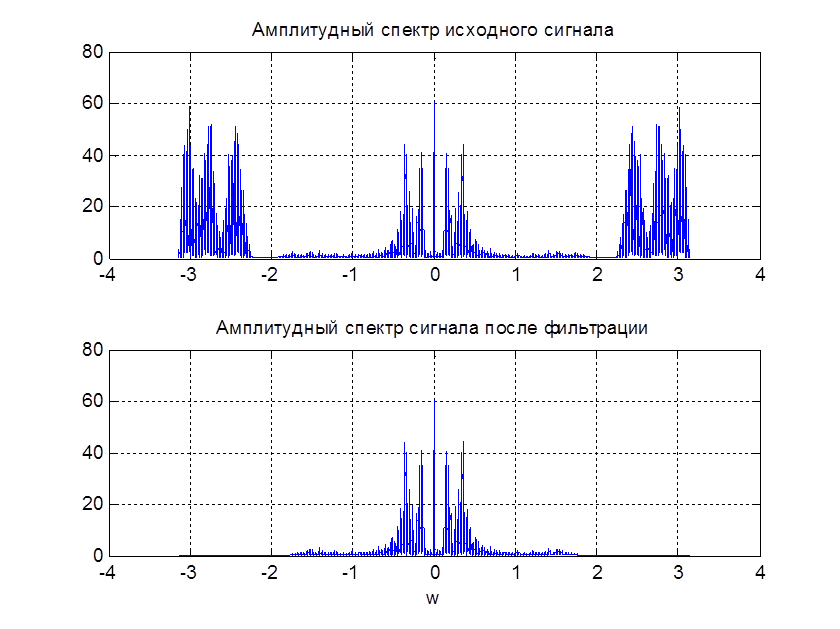
subplot(211), plot(w,abs(Y)), grid
title (‘Амплитудный спектр исходного сигнала’);
subplot(212), plot(w,abs(Y1)), grid
title (‘Амплитудный спектр сигнала после фильтрации’);
Рис. 13. АЧХ сигнала до и после фильтрации
10. Расчет КИХ-фильтра с помощью функции fir1
С помощью следующего кода MATLAB рассчитаем фильтр:
b=fir1(80, 0.55, hann(81));
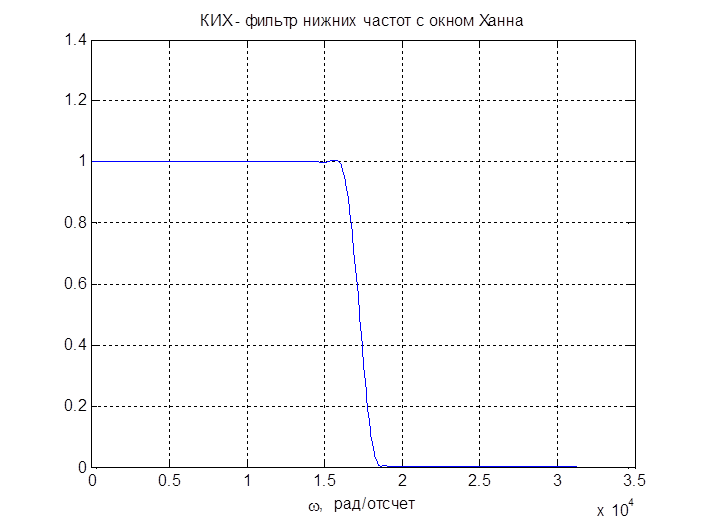
Рис. 14. АЧХ спроектированного фильтра
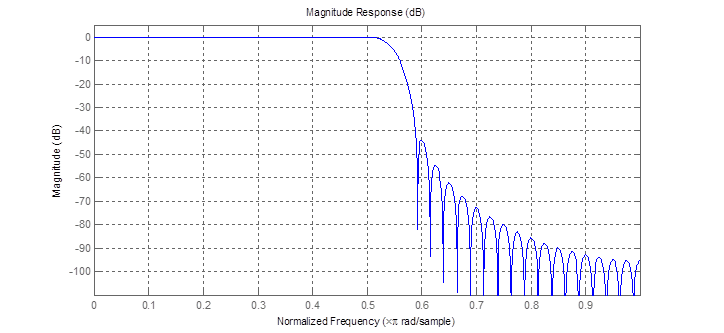
Видим, что АЧХ на рис. 11 и рис. 14 совпадают, значит функция fir1 была использована правильно. Путем масштабирования логарифмической АЧХ (рис. 15) видим, что спецификация фильтра соблюдена
Рис. 15. Логарифмическая АЧХ фильтра
1. Для реализации идеального ФНЧ его аппроксимируют для физического проектирования КИХ – фильтра путём усечения импульсной характеристики до конечной длины N и сдвига на 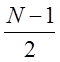
2. В п. 2 (рис. 2 и 3) было показано, что в результате усечения ИХ у реального фильтра по сравнению с идеальным появляются переходная область и пульсации в полосе пропускания и задерживания, объясняющиеся явлением Гиббса. При увеличении N ширина переходной области уменьшается, амплитуда пульсаций не изменяется, но количество их возрастает (рис. 3 – 5).
3. Операцию усечения ИХ фильтра можно представить как умножение на оконную функцию. В данной работе были рассмотрены прямоугольное окно, окна Хэмминга, Ханна, Блэкмана (п. 4 – 6). В Matlab для генерации этих окон используются функции hamming, hann, blackman. По амплитудным спектрам окон (рис. 7) можно судить о параметрах фильтра, который можно получить, применив то или иное окно.
4. Чем шире главный лепесток спектра окна, тем шире переходная полоса фильтра. Амплитуды боковых лепестков влияют на величину пульсаций АЧХ фильтра в полосе пропускания и полосе задерживания.
5. Окно Кайзера (п. 7) предоставляет более гибкие возможности по сравнению с остальными рассмотренными окнами, т.к. имеет параметр β, с помощью которого можно уменьшать уровень боковых лепестков. На рис. 10 – 12 видно, что с увеличением β окно спадает к нулю более плавно, уровень боковых лепестков уменьшается, но одновременно с этим увеличивается ширина главного лепестка.
6. В п. 8 был произведён расчёт фильтра, используя окно Ханна. По графикам АЧХ фильтра (рис. 13 – 14) определены параметры полученного фильтра, которые удовлетворяют исходным требованиям. С помощью спроектированного фильтра отфильтрован сигнал speech и результат фильтрации (рис. 16) соответствует АЧХ фильтра (рис. 13).
1. Сайт http://www.dsplib.ru
2. Лекции по дисциплине «Теория и обработка сигналов» 6 семестр, лектор Щетинин Ю.И.
Чтобы распечатать файл, скачайте его (в формате Word).
Документация
Окно Кайзера
Когда β увеличивается, относительные уменьшения затухания бокового лепестка и mainlobe увеличения ширины. Этот снимок экрана показывает, как относительное затухание бокового лепестка приблизительно остается таким же для фиксированного параметра β, когда длина варьируется.
Примеры окон Кайзера с длиной 50 и параметры β 1, 4, и 9 показывают в этом примере.
Чтобы создать эти окна Кайзера с помощью командной строки MATLAB, введите следующее:
Окна Кайзера в КИХ-проекте
Существует две формулы проекта, которые могут помочь вам спроектировать КИХ-фильтры, чтобы соответствовать набору технических требований фильтра с помощью окна Кайзера. Достигнуть относительного затухания бокового лепестка –α дБ, β ( beta ) параметр
Для ширины перехода Δ ω рад/отсчет, используйте длину
Фильтрует созданный с использованием, эта эвристика выполнит техническим требованиям приблизительно, но необходимо проверить это. Спроектировать фильтр lowpass с частотой среза 0.5 π рад/отсчет, ширина перехода 0.2 π рад/отсчет, и 40 дБ затухания в полосе задерживания, пробует
kaiserord функционируйте оценивает порядка фильтра, частоту среза, и бета параметр окна Кайзера должен был соответствовать данному набору технических требований частотного диапазона.
Пульсация в полосе пропускания является примерно тем же самым как пульсацией в полосе задерживания. Как вы видите из частотной характеристики, этот фильтр почти выполняет техническим требованиям:
Смотрите также
Приложения
Функции
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Документация Signal Processing Toolbox
Поддержка
© 1994-2021 The MathWorks, Inc.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.