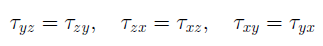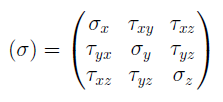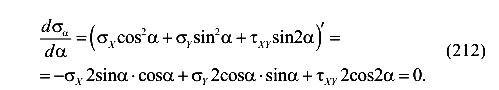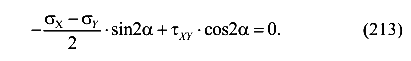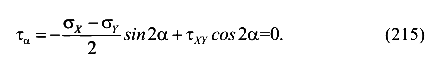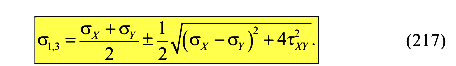что такое главная площадка напряжений
Тензор напряжений.
Главные площадки и главное напряжение.
Виды напряжённого состояния.
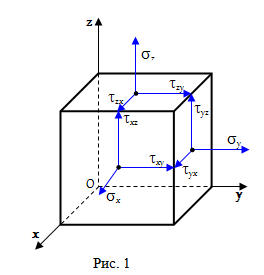
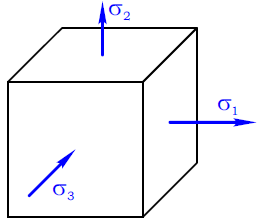
Введем в произвольной точке тела декартову прямоугольную систему координат Oxyz. Рассмотрим в точке O элементарный (бесконечно малый) куб, ребра которого параллельны осям системы координат. Пусть длины ребер куба равны da. Нарисуем на гранях куба нормальные <σx, σy, σz> и касательные
Нормальные напряжения направлены наружу куба и перпендикулярны его граням, а касательные напряжения лежат в плоскостях граней куба. Индекс нормальных напряжений соответствует оси, которой они параллельны. Первая буква двойного индекса касательных напряжений совпадает с индексом нормального напряжения на той же грани. В силу третьего закона Ньютона напряжения на противоположных гранях элементарного куба равны по модулю и противоположны по направлению.
Закон парности касательных напряжений : на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к общему ребру, равны по модулю и направлены обе либо к ребру, либо от ребра:
В курсе «Сопротивление материалов» тензором напряжений называется матрица:
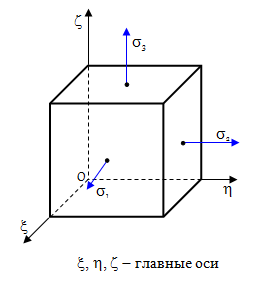
Главные площадки и главные напряжения.
Главными площадками напряжений называются площадки, на которых отсутствуют касательные напряжения.
Виды напряженного состояния.
Виды напряженного состояния: линейное напряженное состояние (два главных напряжения равны нулю), плоское напряженное состояние (одно из главных напряжений равно нулю) и объемное напряженное состояние (все главные напряжения не равны нулю).
Главные площадки и главные напряжения



Нормальные и касательные напряжения на наклонной площадке зависят от ее положения, то есть от направляющих косинусов l, m, n.
Площадки, на которых касательные напряжения равны нулю и действуют только нормальные напряжения, называются главными. Нормальные напряжения на этих площадках называются главными напряжениями.
Предположим, что наклонная площадка с направляющими косинусами l, m, n является главной, то есть вектор нормали к наклонной площадке совпадает с вектором полного напряжения. Тогда нормальное напряжение на этой площадке равно полному напряжению, а касательное напряжение равно нулю (рис.22). Проекции полного напряжения на координатные оси равны:
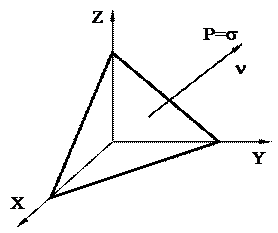 |
В данных уравнениях четыре неизвестных (направляющие косинусы l, m, n и главное напряжение s), поэтому необходимо четвертое уравнение:
Система уравнений имеет ненулевое решение (нулевое не устраивает из-за четвертого уравнения системы), когда равен нулю главный определитель системы:
Сгруппируем слагаемые по степеням главного напряжения
Запишем это уравнение в более компактной форме
Введенные обозначения называются инвариантами напряженного состояния. Так как главные напряжения в точке являются физической характеристикой, то они не зависят от выбора системы координат, а, следовательно, и значения инвариантов также не зависят от выбора системы координат.
Решая кубическое уравнение (37), получим три вещественных корня – три главных напряжения, которые нумеруются в порядке убывания: s1 ³ s2 ³ s3. Подставляя величину главного напряжения в систему (35), можно определить положение главной площадки, т.е. определить ее направляющие косинусы. Три главных площадки в точке взаимно перпендикулярны.
iSopromat.ru
Главными называют нормальные напряжения на площадках рассматриваемого элемента с нулевыми касательными напряжениями.
Для любого случая нагружения бруса всегда можно найти такое положение мысленно выделенного в нем элемента, на гранях которого касательные напряжения будут отсутствовать (т.е. τ=0)
Площадки (грани элемента) на которых касательные напряжения равны нулю называются главными.
Таким образом, главные напряжения – это нормальные напряжения на главных площадках.
Обозначение главных напряжений
Главные напряжения принято обозначать буквой σ с индексом 1, 2 и 3.
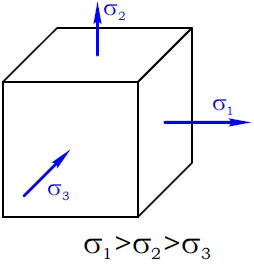
При этом наибольшее, с учетом знака, напряжение обозначается как σ1 а наименьшее соответственно σ3.
Другими словами, главное напряжение, расположенное на числовой оси правее других – σ1, а то, которое левее всех σ3.
Например, для случая объемного напряженного состояния:
При плоском напряженном состоянии:
При линейном напряженном состоянии единственное напряжение всегда обозначается как σ1 или просто σ.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Что такое главная площадка напряжений
Тензор напряжений обладает свойством симметрии. Для доказательства этого свойства рассмотрим приведенный в лекции 5 элементарный параллелепипед с действующими на его площадках компонентами тензора напряжений. Так как тело находится в равновесии, следовательно, находится в равновесии любая его часть, в том числе и элементарный объем. Запишем одно из шести уравнений равновесия этого объема, а именно сумму моментов всех сил относительно оси Ох. Все силы, кроме двух, либо не создают момента относительно ocи Ох, либо взаимно уничтожаются. Отличные от нуля моменты создают компоненты 

После сокращения на элемент объема dV=dxdydz получим
Аналогично, приравнивая нулю сумму моментов всех сил относительно осей Оу и Ог, получим еще два соотношения
Эти условия симметрии и тензора напряжений называются также условиями парности касательных напряжений: касательные напряжения, действующие по двум взаимно перпендикулярным площадкам в направлениях, ортогональных ребру, образованному пересечением этих площадок, равны по величине. С учетом этих свойств из девяти компонент тензора напряжений независимыми оказываются шесть компонент.
Покажем теперь, что компоненты тензора напряжений определенные для трех взаимно перпендикулярных площадок, полностью характеризуют напряженное состояние в точке, т. е. позволяют вычислить компоненты вектора напряжений на площадках, произвольно ориентированных относительно выбранной системы координат. Для этого рассмотрим элементарный объем, образованный сечением параллелепипеда, изображенного на рис. 1, плоскостью, пересекающей координатные оси и имеющей единичный вектор нормали
Рис.1. Элементарный четырехгранник с компонентами напряженного состояния.
п с компонентами nx, ny, nz. На гранях полученного таким образом бесконечно малого тетраэдра действуют напряжения, показанные на рис. 1. При этом вектор напряжений pn на наклонной площадке разложен па составляющие рx, рy, рz вдоль координатных осей. Площади граней, ортогональных координатным осям и вектору нормали, обозначим соответственно dFx, dFy, dFz, dF. Эти площади связаны между собой соотношениями
вытекающими из того, что грани, ортогональные координатным осям, есть проекции наклонной площадки на соответствующую координатную плоскость.
Проектируя силы, действующие на гранях элементарного тетраэдра, на координатные оси, получим уравнения равновесия для рассматриваемого объема. Например, проекции всех поверхностных сил на ось Ох дают
С учетом соотношений (1) после сокращения на dF получим уравнение, связывающее проекцию рx вектора напряжений с соответствующими компонентами тензора напряжений. Объединяя это уравнение с двумя аналогичными уравнениями, полученными проектированием сил на оси Оy и Оz, приходим к следующим соотношениям
носящим название формул Коши. Эти формулы определяют вектор напряжений на произвольно выбранной площадке с вектором п через компоненты тензора напряжений.
Формулы (2) позволяют вычислить через компоненты тензора напряжений
Главные площадки и главные напряжения
Главные площадки и главные напряжения
Если оси 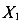
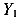
Далее уравнение (219) разделим на 2 и приведем подобные
Слагаемые уравнения (213) умножим на 2, разделим на 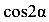
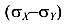
Сравнивая выражение (210) и уравнение (213), убеждаемся, что касательные напряжения на этих площадках равны нулю.
Эти площадки настолько важны в механике твердого деформированного тела, что им присвоено специальное название.
Три взаимно перпендикулярные площадки, на которых касательные напряжения равны нулю, а нормальные напряжения принимают экстремальные значения, называются главными площадками.
Нормальные напряжения, действующие на главных площадках, называются главными напряжениями.
Главные напряжения индексируются цифрами. Для удобства и сокращения записей принята индексация главных напряжений по условию
Главные напряжения для плоского напряженного состояния вычисляются по формуле (без вывода)
Недостающее главное напряжение равно нулю.
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Дополнительные страницы которые вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института