что такое графы в информатике

Теория Графов. Часть 1 Введение и классификация графов

«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена

Введение

Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Схема Московского метро

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.

Отмечу, что число вершин обозначается буквой n:

Число рёбер обозначается буквой m:

Таким образом граф задается и обозначается парой V,E:

Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)

Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.

Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Нулевой граф

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.

Множество E задается парой неупорядоченных вершин множества V.

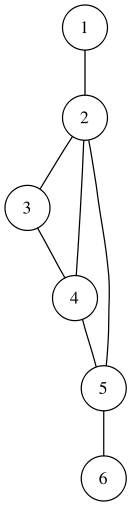
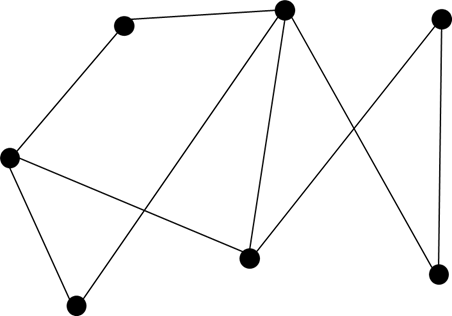
Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =

Граф будет выглядеть следующим образом:

Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.

Степень записывают, как:

Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:

Формула суммы степеней для G = V,E выглядит так:

То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!

А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:

Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?

Классификации графов

Первым признаком классификации является отсутствие или наличие ориентации у ребер.

Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

Неориентированный граф

Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Ориентированный граф

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

Смешанный граф

Вторым признаком является отсутствие или наличие кратных ребер.

Мультиграф

Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.

Заключение

В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.

Источник

Граф (теория графов)

В математической теории графов и информатике граф — это совокупность объектов со связями между ними.

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — это связи, созданные гиперссылками (см. Тематическая карта).

Содержание

Определения

Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Приводимые ниже определения — наиболее часто встречаемые.

V (а значит и E ) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становятся ложными в случае бесконечных множеств.

Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Ориентированный граф

Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v 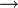w ведёт от вершины v к вершине w.

Смешанный граф

Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.

Прочие связанные определения

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

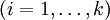
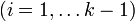
Ориентированным путём в орграфе называют конечную последовательность вершин v_i , для которой все пары (v_i,v_{i + 1}) являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v », является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.

Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов

Ребро графа называется мостом, если его удаление увеличивает число компонент.

Дополнительные характеристики графов

Способы представления графа в информатике

Матрица смежности

Матрица смежности — таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).

Недостатком являются требования к памяти — очевидно, квадрат количества вершин.

Матрица инцидентности

Данный способ является самым ёмким (размер пропорционален | E | | V | ) и неудобным для хранения, но облегчает нахождение циклов в графе.

Список рёбер

Список рёбер — это тип представления графа в памяти, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.

Обобщение понятия графа

Простой граф является одномерным симплициальным комплексом.

Более абстрактно, граф можно задать как тройку , где V и E — некоторые множества (вершин и рёбер, соотв.), а — функция инцидентности (или инцидентор), сопоставляющая каждому ребру (упорядоченную или неупорядоченную) пару вершин u и v из V (его концов). Частными случаями этого понятия являются:

Под данное выше определение не подходят некоторые другие обобщения:

Литература

См. также

Ссылки

Популярные программы для визуализации графов

Источник

Что такое графы в информатике

Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер.

Классификация графов

В связном графе между любой парой вершин существует как минимум один путь.

В несвязном графе существует хотя бы одна вершина, не связанная с другими.

Графы также подразделяются на

В ориентированном графе ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.

В неориентированном графе по каждому из ребер можно осуществлять переход в обоих направлениях.

Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер.

Способы представления графа

Граф может быть представлен (сохранен) несколькими способами:

Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Размер массива зависит от количества вершин и/или ребер в конкретном графе.

Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1.
Число строк матрицы смежности равно числу столбцов и соответствует количеству вершин графа.

Когда из одной вершины в другую проход свободен (имеется ребро), в ячейку заносится 1, иначе – 0. Все элементы на главной диагонали равны 0 если граф не имеет петель.

Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).

В неориентированном графе если вершина инцидентна ребру то соответствующий элемент равен 1, в противном случае элемент равен 0.

Матрица инцидентности для своего представления требует нумерации рёбер, что не всегда удобно.

Список смежности (инцидентности)
Если количество ребер графа по сравнению с количеством вершин невелико, то значения большинства элементов матрицы смежности будут равны 0. При этом использование данного метода нецелесообразно. Для подобных графов имеются более оптимальные способы их представления.

По отношению к памяти списки смежности менее требовательны, чем матрицы смежности. Такой список можно представить в виде таблицы, столбцов в которой – 2, а строк — не больше, чем вершин в графе.
В каждой строке в первом столбце указана вершина выхода, а во втором столбце – список вершин, в которые входят ребра из текущей вершины.

Преимущества списка смежности:

Недостатки списка смежности:

Алгоритмы обхода графов

Основными алгоритмами обхода графов являются

Поиск в ширину подразумевает поуровневое исследование графа:

Вершины просматриваются в порядке возрастания их расстояния от корня.
Алгоритм прекращает свою работу после обхода всех вершин графа, либо в случае выполнения требуемого условия (например, найти кратчайший путь из вершины 1 в вершину 6).
Каждая вершина может находиться в одном из 3 состояний:

Фиолетовый – рассматриваемая вершина.

Применения алгоритма поиска в ширину

Алгоритм поиска в ширину работает как на ориентированных, так и на неориентированных графах.
Для реализации алгоритма удобно использовать очередь.

Реализация на C++ (с использованием очереди STL)

Результат выполнения

Задача поиска кратчайшего пути
Реализация на С++

Поиск в глубину – это алгоритм обхода вершин графа.

Поиск в ширину производится симметрично (вершины графа просматривались по уровням). Поиск в глубину предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность продвижения означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина).

Отсутствие последнего свидетельствует об одной из двух возможных ситуаций:

Каждая вершина может находиться в одном из 3 состояний:

Фиолетовый – рассматриваемая вершина.

Применения алгоритма поиска в глубину

Алгоритм поиска в глубину работает как на ориентированных, так и на неориентированных графах. Применимость алгоритма зависит от конкретной задачи.
Для реализации алгоритма удобно использовать стек или рекурсию.

Реализация на C++ (с использованием стека STL)

Результат выполнения

Задача поиска лексикографически первого пути на графе.
Реализация на C++

Результат выполнения

Поиск в глубину также может быть реализован с использованием рекурсивного алгоритма.

Реализация обхода графа в глубину на C++ (с использованием рекурсии)

Источник

Графические информационные модели. Графы

Урок 6. Информатика 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Графические информационные модели. Графы»

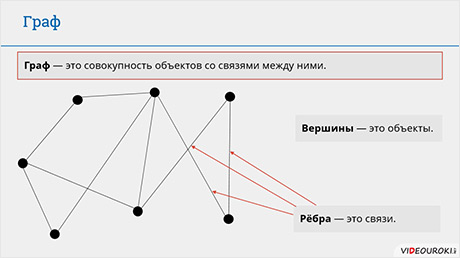
Граф – это совокупность объектов со связями между ними. Графически это будет выглядеть следующим образом:

Вершины (точки) – это объекты, а ребра (линии между ними) – это связи. Помимо точек вершины графа могут изображаться овалами, кругами, прямоугольниками и так далее. Связи между вершинами могут быть различными: дуги, рёбра, петли.

На данном уроке мы с вами познакомимся с ориентированными и неориентированными графами. В ориентированном графе связями между вершинами будут дуги, а в неориентированном – рёбра.

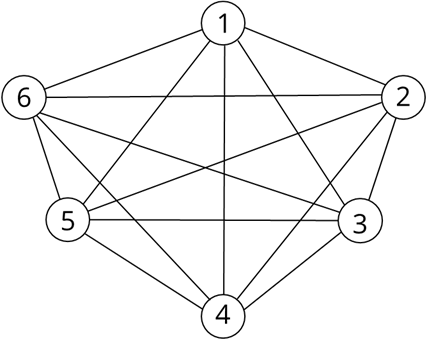
Решим задачу: В соревнованиях по шахматам участвовало 6 учащихся с 9 по 11 класс. При встрече они все обменялись рукопожатиями. Вопрос: сколько всего было сделано рукопожатий?

Для решения данной задачи будем использовать граф. Вершинами графов будут являться шесть учащихся, которые участвовали в турнире. Пронумеруем их от одного до шести. Проведем от каждой вершины линии (ребра) к оставшимся пяти вершинам.

Для ответа на вопрос остается сосчитать, сколько линий изображено на графе. Ответ: на турнире было сделано 15 рукопожатий.

Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.

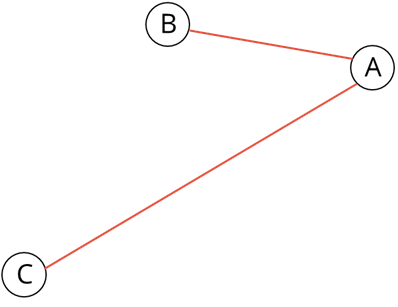
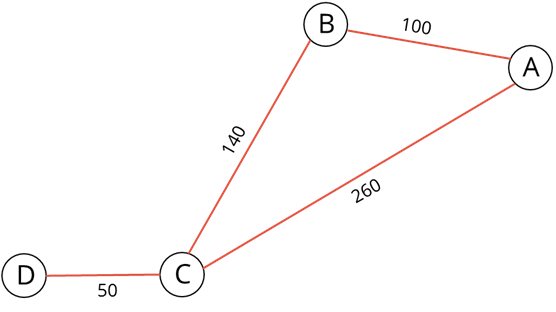
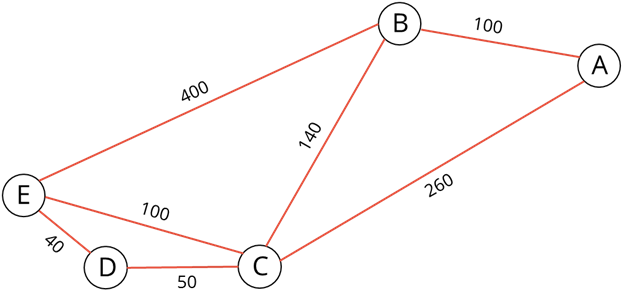
Давайте сами нарисуем взвешенный граф на основе задачи со следующим условием: Между городами A, B, C, D, Е построены дороги. Необходимо найти кратчайший путь из города А в город Е, если известно, что из города А в город В расстояние 100 километров, из А в С – 260 километров, из В в С – 140 километров, из В в Е – 400 километров, из С в D – 50 километров, из С в Е – 100 километров и из D в Е – 40 километров.

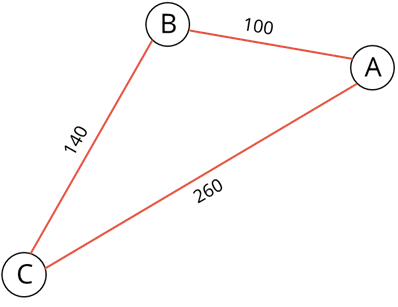
Итак, для решения данной задачи необходимо нарисовать взвешенный граф, так как нам дано расстояние, то есть вес рёбер. Для начала нарисуем вершину А. Из неё будут выходить два ребра в вершины В и С. Ребро из А в В будет короче, чем из А в С, так как расстояние из пункта А в пункт В 100 километров, а из пункта А в пункт С – 260 километров.

Далее нарисуем ребро из В в С и его вес будет равен 140.

Теперь нарисуем ребро из вершины С в вершину D и укажем вес 50

У нас получился взвешенный граф.

Нам осталось найти кратчайший путь. Для этого из вершины А будем идти в вершину В – это 100 километров, затем сразу в вершину Е. Слаживаем 100 и 400, получим 500 километров.

В свою очередь, цикл – это цепь, в которой начальная и конечная вершины совпадают. В детстве, наверное, каждый из вас рисовал звезду, не отрывая ручки от бумаги и не проходя дважды по одной и той же линии или ребру. При изображении такой звезды начальная и конечная вершины совпадают. Сеть – это граф с циклом.

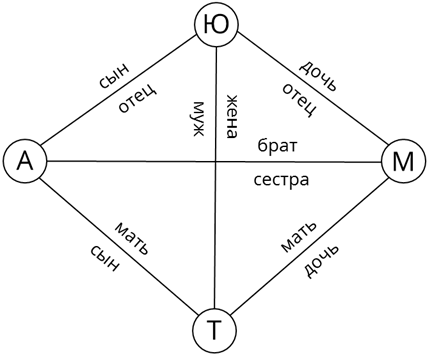
Разберём ещё один пример. У Антона в семье есть мама Татьяна, папа Юрий и сестра Маша. Изобразим каждого члена семьи как вершину нашего графа и обозначим первыми буквами имён. От каждого из них проведём рёбра к оставшимся троим. Над каждым из рёбер укажем, кто кем и кому приходится. Например, если идти от вершины Антона к Юрию, то Антон является сыном. А если идти наоборот, от Юрия к Антону, то Юрий является отцом. Аналогичным образом можно провести отношения между всеми членами семьи. Данный граф является примером семантической, или же смысловой сети.

Таким образом, Семантическая сеть – это информационная модель, имеющая вид графа, вершинам которого соответствуют определённые объекты, а рёбра задают отношения между ними. Все связи данного графа различны, поэтому их необходимо подписывать.

Графы широко распространены как информационные модели. Их можно применять, например, при планировании жилого района, где вершинами будут являться дома, а рёбрами – дороги или дорожки, которые их связывают. Ещё одним примером будет являться карта проезда по городу на любом из видов транспорта, где остановки – это вершины, а путь движения транспорта – это рёбра и так далее.

Следующее определение в данной теме: дерево. Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину. Отличительная особенность дерева: между любыми двумя его вершинами существует единственный путь. Корень дерева – это одна и единственная главная его вершина.

Каждая вершина дерева (кроме корня) имеет только одного предка. Обозначенный предком объект входит в один класс высшего уровня. Любая вершина дерева может порождать несколько потомков. Потомки – это вершины, которые соответствуют классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Листья – это вершины, которые не имеют потомков.

Разберёмся более подробно на примере:

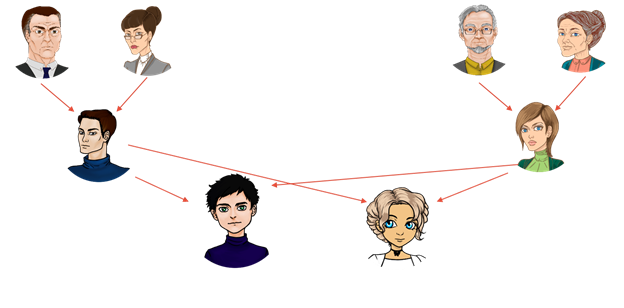
Ученик Антон решил составить генеалогическое дерево своей семьи. Для этого ему необходимо было узнать, кто в каких отношениях находится. То есть он является сыном своего отца Юрия и мамы Татьяны. В свою очередь Татьяна является дочерью Леонида (дедушки Антона) и Елены (бабушки Антона). Юрий является сыном Григория (дедушки Антона) и Марии (бабушки Антона). У Антона есть сестра Маша. Так как словесное описание трудно для восприятия, давайте поможем Антону представить это все в виде дерева и построим генеалогическое дерево.

Видим, что самыми старшими являются дедушки и бабушки Антона, поэтому расположим их в самом верху. У Леонида и Елены есть дочь Татьяна, а у Григория и Марии сын Юрий. Значит, разместим их на втором уровне (если считать сверху) и укажем их отношения с родителями в виде стрелок. У Татьяны и Юрия есть сын Антон и дочь Маша. Разместим их аналогичным образом на нашей схеме.

Таким образом, мы построили родословное дерево.

· Граф – это совокупность объектов со связями между ними.

· Вершины – это объекты, а ребра – это связи.

· Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.

· Цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза.

· Цикл – это цепь, в которой начальная и конечная вершины совпадают.

· Сеть – это граф с циклом.

· Семантическая сеть – это информационная модель, имеющая вид графа, вершинам которого соответствуют определённые объекты, а рёбра задают отношения между ними.

· Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину.

Источник