что такое оценка параметра

Понятие оценки параметров.

Проблемы статистических выводов традиционно делятся на проблемы оценивания и проверку гипотез. Главное различие между этими двумя проблемами состоит в том, что при оценивании мы должны определить величину параметра или нескольких параметров. В то время как при проверке гипотез мы должны решить: принять или отвергнуть специфическую величину (или ряд специфических величин) параметра или нескольких параметров.

В общем виде задача оценки параметров формулируется следующим образом.

1. Оценка θ_n параметра θ называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е. M(θ_n) = θ.

В противном случае оценка называется смещенной. Если это равенство не выполняется, то оценка θ_n, полученная по разным выборкам, будет либо завышать θ, если M(θ_n) > θ, либо занижать его, если M(θ_n) 2 есть дисперсия 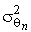, то эффективность является решающим свойством, определяющим качество оценки.

В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности.

4. Оценка θ_n параметра θ является достаточной, если при заданном ее значении распределение наблюдения Х не зависит от параметра θ. Иначе, оценка θ_n обеспечивает оценку параметра без потери информации, содержащейся в выборке.

Однако на практике не всегда оценки удовлетворяют всем трем требованиям. Может оказаться, что даже если эффективная оценка существует, то формулы для ее вычисления оказываются слишком сложными, и тогда используют оценку, дисперсия которой несколько больше. Иногда, в интересах простоты расчетов, применяются незначительно смещенные оценки. Выбору оценки всегда должно предшествовать ее критическое рассмотрение.

Источник

Глава 3 Оценка параметров

Цель любого физического эксперимента — проверить, выполняется ли некоторая теоретическая закономерность ( модель ), а также получить или уточнить её параметры. Поскольку набор экспериментальных данных неизбежно ограничен, а каждое отдельное измерение имеет погрешность, можно говорить лишь об оценке этих параметров. В большинстве случаев измеряется не одна величина, а некоторая функциональная зависимость величин друг от друга. В таком случае возникает необходимость построить оценку параметров этой зависимости.

Для построения оценки нужны следующие компоненты

процедура построения оценки параметров по измеренным данным («оценщик»):

Рассмотрим самые распространенные способы построения оценки.

3.1 Метод минимума хи-квадрат

Обозначим отклонения результатов некоторой серии измерений от теоретической модели y = f ⁢ ( x | θ ) как

где θ — некоторый параметр (или набор параметров), для которого требуется построить наилучшую оценку. Нормируем Δ ⁢ y i на стандартные отклонения σ i и построим сумму

Можно показать (см. [ 5 ] ), что оценка по методу хи-квадрат является состоятельной, несмещенной и, если данные распределены нормально, имеет максимальную эффективность (см. приложение 5.2 ).

3.2 Метод максимального правдоподобия.

Рассмотрим кратко один из наиболее общих методов оценки параметров зависимостей — метод максимума правдоподобия.

Сделаем два ключевых предположения:

зависимость между измеряемыми величинами действительно может быть описана функцией y = f ⁢ ( x | θ ) при некотором θ ;

все отклонения Δ ⁢ y i результатов измерений от теоретической модели являются независимыми и имеют случайный (не систематический!) характер.

3.3 Метод наименьших квадратов (МНК).

Оценка по методу наименьших квадратов (МНК) удобна в том случае, когда не известны погрешности отдельных измерений. Однако тот факт, что метод МНК игнорирует информацию о погрешностях, является и его основным недостатком. В частности, это не позволяет определить точность оценки (например, погрешности коэффициентов прямой σ k и σ b ) без привлечения дополнительных предположений (см. п. 3.6.2 и 3.6.3 ).

3.4 Проверка качества аппроксимации

В теории вероятностей доказывается (см. [ 4 ] или [ 5 ] ), что ожидаемое среднее значение (математическое ожидание) суммы χ 2 в точности равно числу степеней свободы:

3.5 Оценка погрешности параметров

Легко убедиться, что:

Вероятностное содержание этого интервала будет равно 68% (его еще называют 1– σ интервалом). Отклонение χ 2 на 2 будет соответствовать уже 95% доверительному интервалу.

3.6 Методы построения наилучшей прямой

3.6.1 Метод наименьших квадратов

Пусть сумма квадратов расстояний от точек до прямой минимальна:

Данный метод построения наилучшей прямой называют методом наименьших квадратов (МНК).

Напомним, что угловые скобки означают усреднение по всем экспериментальным точкам:

Эти соотношения и есть решение задачи о построении наилучшей прямой методом наименьших квадратов.

3.6.2 Погрешность МНК в линейной модели

Пользуясь в этих предположениях формулами для погрешностей косвенных измерений (см. раздел ( 2.6 )) можно получить следующие соотношения:

В частном случае y = k ⁢ x :

3.6.3 Недостатки и условия применимости МНК

Формулы ( 3.7 ) (или ( 3.6 )) позволяют провести прямую по любому набору экспериментальных данных, а полученные выше соотношения — вычислить соответствующую среднеквадратичную ошибку для её коэффициентов. Однако далеко не всегда результат будет иметь физический смысл. Перечислим ограничения применимости данного метода.

В первую очередь метод наименьших квадратов — статистический, и поэтому он предполагает использование достаточно большого количества экспериментальных точек (желательно 10″ display=»inline»> n > 10 ).

Наконец, стоит предостеречь от использования любых аналитических методов «вслепую», без построения графиков. В частности, МНК не способен выявить такие «аномалии», как отклонения от линейной зависимости, немонотонность, случайные всплески и т.п. Все эти случаи требуют особого рассмотрения и могут быть легко обнаружены визуально при построении графика.

3.6.4 Метод хи-квадрат построения прямой

Пусть справедливы те же предположения, что и для метода наименьших квадратов, но погрешности σ i экспериментальных точек различны. Метод минимума хи-квадрат сводится к минимизации суммы квадратов отклонений, где каждое слагаемое взято с весом w i = 1 / σ i 2 :

Этот метод также называют взвешенным методом наименьших квадратов.

Определим взвешенное среднее от некоторого набора значений < x i >как

где W = ∑ i w i — нормировочная константа.

Повторяя процедуру, использованную при выводе ( 3.7 ), нетрудно получить (получите) совершенно аналогичные формулы для искомых коэффициентов:

Источник

оценка параметра

Смотреть что такое «оценка параметра» в других словарях:

Оценка (значения) — Оценка (в философии) способ установления значимости чего либо для действующего и познающего субъекта. Оценка (педагогика) выраженное в числе мнение преподавателя (другого проверяющего лица) об уровне знаний ученика (качестве его работы) Оценка (в … Википедия

оценка телеметрируемого параметра — Значение параметра или функциональная зависимость его от времени или другого аргумента, полученные по результатам обработки телеметрических сообщений. Примечание Оценка может отличаться от истинного значения наличием внесенных погрешностей. [ГОСТ … Справочник технического переводчика

Оценка (значение) — Оценка (метрология) в метрологии, приближённое значение величины или параметра, найденное по экспериментальным данным Оценка (философия) способ установления значимости чего либо для действующего и познающего субъекта. Оценка (экономика) процесс… … Википедия

Оценка — (метрология) в метрологии, приближённое значение величины или параметра, найденное по экспериментальным данным Оценка (философия) способ установления значимости чего либо для действующего и познающего субъекта. Оценка (экономика) процесс… … Википедия

ОЦЕНКА СТАТИСТИЧЕСКАЯ — функция от случайных величин, применяемая для оценки неизвестных параметров теоретич. распределения вероятностей. Методы теории О. с. служат основой современной теории ошибок; обычно в качестве неизвестных параметров выступают измеряемые физич.… … Математическая энциклопедия

оценка — 3.9 оценка (evaluation): Систематическое определение степени соответствия объекта установленным критериям. Источник: ГОСТ Р ИСО/МЭК 12207 99: Информационная технология. Процессы жизненного цикла программных средств … Словарь-справочник терминов нормативно-технической документации

Оценка телеметрируемого параметра — 18. Оценка телеметрируемого параметра Е. Telemetering parameter estimation Значение параметра или функциональная зависимость его от времени или другого аргумента, полученные по результатам обработки телеметрических сообщений. Примечание. Оценка… … Словарь-справочник терминов нормативно-технической документации

Оценка максимального правдоподобия — Метод максимального правдоподобия в математической статистике это метод оценивания неизвестного параметра путём максимизации функции правдоподобия. (Фишер 1912 г.[1]) Содержание 1 Определение 2 Замечание 3 Примеры … Википедия

оценка — Этим термином обозначают несколько близких, но неодинаковых, понятий, каждому из которых соответствует свой английский термин. Прежде всего, оценка (estimator) – это функция, алгоритм, словом, способ получить по выборке число (estimate), которое… … Словарь социологической статистики

ОЦЕНКА, СТАТИСТИЧЕСКАЯ — функция выборочных наблюдений для приближенной замены параметра распределения (или самого распределения). Например, для нормального распределения случайной величины средняя арифметическая – оценка математического ожидания. Точечная и интервальная … Большой экономический словарь

Источник

Статистическая оценка параметров

Основной задачей математической статистики является разработка методов получения научно обоснованных выводов о массовых явлениях и процессах из данных наблюдений или экспериментов.

Вся подлежащая изучению совокупность объектов называется генеральной совокупностью. Та часть объектов, которая была отобрана из генеральной совокупности, называется выборочной совокупностью или, более коротко, выборкой. Число элементов генеральной или выборочной совокупности называется объемом. Договоримся, обозначать объем выборки буквой n, а объем генеральной совокупности буквой N.

Выборка, в общем случае, образуется для оценки каких-либо характеристик генеральной совокупности. Однако не всякая выборка может быть действительным представлением о генеральной совокупности. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности необходимо, чтобы объект выборки правильно его представлял. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируется так: выборка должна быть репрезентативной (или представительной). Репрезентативность выборки обеспечивается случайностью отбора. При случайном отборе все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку.

При исследовании какой-либо генеральной совокупности важно знать числовые характеристики наблюдаемых признаков (среднее значение, дисперсию и др.). Однако генеральная совокупность неизвестна, и судить о ней приходится по выборке. Но состав выборки случаен, поэтому выводы о параметрах генеральной совокупности, сделанные на основании выборочных данных, тоже будут иметь случайный характер. Следовательно, ни при каком объёме выборки, вообще говоря, нельзя получить точное значение неизвестного параметра q, а можно лишь найти его приближённое значение , которое называется оценкой неизвестного параметра по выборке.

Поскольку любая выборка является случайной величиной, то любая оценка, полученная по выборочным данным, тоже будет случайной величиной. Следовательно, можно говорить о математическом ожидании, дисперсии и функции распределения оценки. Выбор оценки, позволяющей получить «хорошее» приближение оцениваемого параметра – основная задача статистического оценивания.

Статистическая оценка называется точечной, если она выражается одним числом. Точечными оценками соответствующих показателей генеральной совокупности служат определённые характеристики выборочной совокупности. Вообще говоря, можно получить много различных формул (или, как говорят, статистик) для вычисления тех или иных оценок. Все эти формулы должны удовлетворять следующим требованиям:

1. Оценки должны быть состоятельными, т.е. при увеличении объёма выборки возрастает вероятность того, что полученная оценка будет сколь угодно мало отличаться от истинного значения.

2. Оценки должны быть несмещёнными, т.е. . Это требование гарантирует отсутствия систематических ошибок при оценке параметров. Однако, если оценка является состоятельной, то при большом объёме выборки требованием несмещённости часто пренебрегают.

3. Оценки должны быть эффективными, т.е. . Вопрос о нахождении эффективных оценок является наиболее сложным в теории оценивания. Поэтому на практике часто используют оценки, которые не являются эффективными.

(3.13)

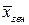
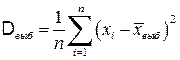
является состоятельной и несмещенной оценкой среднего значения генеральной совокупности. Эта оценка является эффективной в классе линейных несмещенных оценок.

(3.14)

является состоятельной, но смещенной оценкой дисперсии 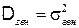генеральной совокупности. Выборочная дисперсия оценивает генеральную дисперсию с недостатком, поэтому в качестве оценки дисперсии лучше брать исправленную дисперсию:

. (3.15)

Исправленная дисперсия s 2 является состоятельной и несмещенной оценкой дисперсии генеральной совокупности. Из состоятельности оценок s 2 и D_выб следует, что при больших выборках (обычно при n>50) разности между ними практически нет. Если выборка взята из нормально распределённой генеральной совокупности, то оценка дисперсии s 2 будет оптимальной.

После получения точечной оценки желательно иметь данные о надежности такой оценки. Понятно, что величина является лишь приближенным значением параметра q. Вычисленная точечная оценка может быть близка к оцениваемому параметру, а может и очень сильно отличаться от него. Точечная оценка не несет информации о точности процедуры оценивания. Особенно важно иметь сведения о надежности оценок для небольших выборок. В таких случаях следует пользоваться интервальными оценками.

Задачу интервального оценивания в самом общем виде можно сформулировать следующим образом: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри этого интервала находится оцениваемый параметр. Здесь существует несколько подходов. Наиболее распространенным методом интервального оценивания является метод доверительных интервалов.

Доверительным интервалом для параметра q называется интервал , содержащий неизвестное значение параметра генеральной совокупности с заданной вероятностью g, т.е.

.

Число g называется доверительной вероятностью, а число a=1–g – уровнем надежности. Доверительная вероятность задается априорно и определяется конкретными условиями. Обычно используется g=0,9; 0,95; 0,99 (соответственно, a=0,1; 0,05; 0,01).

Длина доверительного интервала, характеризующая точность интервальной оценки, зависит от объема выборки n и доверительной вероятности g. При увеличении величины n длина доверительного интервала уменьшается, а с приближением вероятности g к единице – увеличивается.

Часто доверительный интервал строят симметричным относительно точечной оценки, т.е. в виде

, (3.16)

.

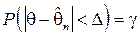
Здесь число D называется предельной (или стандартной) ошибкой выборки.

Пусть количественный признак X генеральной совокупности имеет нормальное распределение с заданной дисперсией s 2 и неизвестным математическим ожиданием a. Для оценки параметра a извлечена выборка x₁, x₂, …, x_n, состоящей из n независимых нормально распределенных случайных величин с параметрами a и s, причем s известно, а величину a оценивают по выборке:

.

Тогда, . Если воспользоваться теперь формулой нахождения вероятности отклонения нормально распределенной случайной величины от математического ожидания, получим доверительный интервал оценки среднего значения генеральной совокупности при известной дисперсии:

, (3.17)

, (3.18)

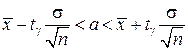
где – предельная ошибка выборки, – средняя ошибка выборки.

Число t_g определяется из равенства . Приведем значения t_g для широко распространенных значений доверительной вероятности:

, , .

Пример 3.2. На основе продолжительных наблюдений за весом X пакетов орешков, заполняемых автоматически, установлено, что среднее квадратичное отклонение веса пакетов равно s=10 г. Взвешено 25 пакетов, при этом их средний вес составил . В каком интервале с надежностью 95% лежит истинное значение среднего веса пакетов?

Решение. Логично считать, случайная величина X имеет нормальный закон распределения: . Найдем среднюю ошибку выборки

.

Для определения 95%-го доверительного интервала вычислим предельную ошибку выборки

.

Следовательно 95%-й доверительный интервал для истинное значение среднего веса пакетов будет иметь вид

,

.

Выше была решена задача построения интервальной оценки для математического ожидания нормального распределения, когда его дисперсия известна. Однако на практике дисперсия обычно тоже неизвестна и ее вычисляют по той же самой выборке, что и математическое ожидание. Это приводит к необходимости использования другой формулы при определении доверительного интервала для математического ожидания случайной величины, имеющей нормальное распределение. Такая постановка задачи особенно актуальна при малых объемах выборки.

Пусть количественный признак X генеральной совокупности имеет нормальное распределение N(a,s), причем оба параметра a и s неизвестны. По данным выборки x₁, x₂, …, x_n, вычислим среднее арифметическое и исправленную дисперсию:

, .

Для нахождения доверительного интервала в этом случае строится статистика

, (3.19)

имеющая распределение Стьюдента с числом степеней свободы n=n–1 независимо от значений параметров a и s. Отсюда находят интервальную оценку для среднего значения генеральной совокупности при неизвестном s:

, (3.20)

, (3.21)

где – предельная ошибка выборки. Число t (коэффициент Стьюдента) находится из таблиц для распределения Стьюдента. Отметим, что он является функцией двух аргументов: доверительной вероятности g и числа степеней свободы n=n–1, т.е. t=t(g,n).

Следует быть очень внимательным при использовании таблиц для распределения Стьюдента. Во-первых, обычно в таблицах вместо доверительной вероятности g используют уровень надежности a=1–g. Во-вторых, очень часто в таблицах приводятся значения т.н. одностороннего критерия Стьюдента

, или .

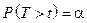
В этом случае в таблицах следует брать значения , если в таблице используется уровень надежности, или , если в таблице используется доверительная вероятность.

Несмотря на кажущееся сходство формул (3.17) и (3.20), между ними имеется существенное различие, заключающееся в том, что коэффициент Стьюдента t зависит не только от доверительной вероятности, но и от объема выборки. Особенно это различие заметно при малых выборках. (Напомним, что при больших выборках различие между распределением Стьюдента и нормальным распределением практически исчезает.) В этом случае использование нормального распределения приводит к неоправданному сужению доверительного интервала, т.е. к неоправданному повышению точности. Например, если n=5 и g=0,99, то, пользуясь распределением Стьюдента, получим t=4,6, а используя нормальное распределение, – t=2,58, т.е. доверительный интервал в последнем случае почти в два раза уже, чем интервал при использовании распределения Стьюдента.

Пример 3.3. Аналитик фондового рынка оценивает среднюю доходность определенных акций. Случайная выборка 15 дней показала, что средняя (годовая) доходность со средним квадратичным отклонением . Предполагая, что доходность акций подчиняется нормальному закону распределения (с параметрами a=10,37 и ), постройте 95%-доверительный интервал для средней доходности интересующего аналитика вида акций.

Решение. Поскольку объем выборки n=15 небольшой, то для построения доверительного интервала для математического ожидания (генеральной средней) необходимо применить распределение Стьюдента с степенями свободы. По условиям задачи доверительная вероятность равна g=0,95, т.е. уровень надёжности равен a=0,05. По таблицам для распределения Стьюдента находим

.

Используя это значение, строим 95%-доверительный интервал:

,

.

Следовательно, аналитик может быть на 95% уверен, что средняя годовая доходность по акциям находится между 8,44% и 12,3%.

Пример 3.4. Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания отклонения, вычисленного в примере 3.1, с доверительной вероятностью g=0,95.

Решение. Поскольку выборочная дисперсия является смещенной оценкой, вычисляем исправленную выборочную дисперсию:

.

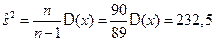
Тогда среднеквадратичное отклонение равно

.

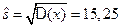
Найдем коэффициент Стьюдента. В рассматриваемом случае n=90, следовательно n=n–1=89. Тогда, при g=0,95 (или a=0,05) по таблицам для распределения Стьюдента находим:

.

В результате получаем (см. формулу (3.20))

.

.

Источник