Что в русском языке обозначается треугольником

Частица – что это за часть речи, что про нее надо знать и как правильно подчеркивать частицы в предложениях

Служебная часть речи. Вносит в предложение «оттенки смысла».

Частица – это одна из трех служебных частей речи. Две другие: предлог и союз. Частицы нужны для того, чтобы дополнить смысл предложения, внести «оттенки» смысла. Давайте разберемся, как это происходит.

Зачем нужны частицы

Они привносят дополнительный смысл. Сравните: «Я сказал, чтобы ты был дома в десять!» – «Я же сказал, чтобы ты был дома в десять!». Частица «же» внесла в предложение какой-то оттенок раздражения. Человек как будто хочет сказать: «Ты что, глупый?! Ты меня не услышал?!»

Другой пример. «На улице очень холодно» – «На улице не очень холодно». Отрицание, которое выражено частицей «не» помогло говорящему точнее передать свою мысль. Получается как бы три возможных варианта: не очень холодно – холодно – очень холодно. Говорящий посчитал, что ему подойдет первый – то есть «холодно», но все-таки терпимо.

С помощью частиц можно задавать вопросы: «Ты ли это?». А еще можно задать вопрос и вместе с ним выразить какое-то чувство, например, отчаяние: «Неужели мы никогда больше не вернемся» – человек спрашивает как будто самого себя, сам не может поверить, что пути назад нет.

Частицы могут использоваться для образования форм слова. Например, чтобы получить глагол в сослагательном наклонении, мы используем частицу «бы»: «Я бы учился на пятерки … [при таком-то условии]».

Три признака частицы

Эти признаки характерны для всех служебных слов.

Как найти частицу в предложении

Это можно сделать методом «исключения». Сначала вы исключите все самостоятельные слова, к которым можно задать вопрос. Потом у вас останутся служебные – предлоги, союзы и частицы.

Предлог всегда будет относиться к существительному и употребляться в вопросе к нему. Даже если он стоит не рядом с существительным: «песня (про что?) про храброго зайца». Предлог нельзя «выбросить» из предложения, потому что получится бессмыслица или совсем другое значение «песня храброго зайца» (то есть уже не про него, а его песня, которую он сам поет), «иду школу», «купил магазине» и так далее.

Союзы будут соединять слова или предложения. Смотрите: рисую и читаю; корабли и капитаны; «Подул ветер и мы укрылись в пещере».

А частицы ничего не соединяют, в вопросах к существительным не употребляются. Их почти всегда можно выбросить из предложения без потери смысла: «Ты же человек» – «Ты человек», «Пойдешь ли ты гулять со мной?» – «Ты пойдешь гулять со мной?».

А вообще, лучше гуглить

Если вы плохо знаете морфологию, то лучше гуглите непонятные слова. Например «либо – какая часть речи», «же – какая часть речи». Так вы быстрее будете их запоминать.

И еще. Слова могут быть разными частями речи в зависимости от контекста. Поэтому не доверяйте быстрым ответам Гугла и Яндекса, открывайте целиком сайты и смотрите объяснение, почему слово относится к той или иной части речи.

Разряды частиц

Их не надо учить, но они помогают запомнить сами частицы. Вот вам разряды с примерами, частицы я в каждом примере выделю полужирным.

Как подчеркивать частицы в предложении

Поскольку они не являются членами предложения, их подчеркивать не надо. Но в школьной практике бывает иначе. Некоторые учителя говорят, что надо подчеркивать вместе с тем словом, к которому частица относится. Например: «Я не рассказал друзьям о происшедшем» – частица «не» относится к сказуемому «рассказал», поэтому подчеркивается вместе с ним двойной линией.

Некоторые учителя велят выделять служебные слова, например, в треугольник. Я думаю, что это более рационально, помогает ребенку «видеть» служебные части речи в предложении.

Уточните у своего учителя, как подчеркивать предлоги, союзы и частицы и подчеркивайте так, как он/она скажет.

Полезные материалы по теме

Прокрутите чуть ниже – вы увидите форму для комментариев. Там можно написать вопросы по теме, если они у вас есть. Я отвечаю на все вопросы.

Покритиковать статью там тоже можно.

Вот подборка курсов по русскому языку. В них есть несколько бесплатных материалов и книг для скачивания. Все разделено по классам, выберите свой класс по содержанию и посмотрите материал. Может, подберете что-то хорошее.

Подпишитесь на рассылку, чтобы получать новые статьи по русскому языку.

Источник

Треугольник

Треуго́льник (в евклидовом пространстве) — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла. Если три точки лежат на одной прямой, то «треугольник» с вершинами в трёх данных точках называется вырожденным. Все остальные треугольники невырожденные.

В неевклидовых пространствах в качестве сторон треугольника выступают геодезические линии, которые, как правило, являются криволинейными. Поэтому такие треугольники называют криволинейными.

Содержание

Элементы треугольника

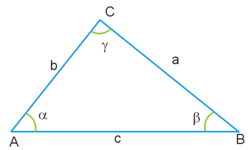
Треугольник с вершинами A, B и C обозначается как (см. рис.). Треугольник имеет три стороны:

Длины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):

Треугольник имеет следующие углы:

Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α, β, γ).

Признаки равенства треугольников

Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:

Признаки равенства прямоугольных треугольников:

В сферической геометрии и в геометрии Лобачевского существует признак равенства треугольников по трём углам.

Типы треугольников

Типы треугольников
Файл:Triangle-acute.svg Остроугольный	Файл:Triangle-obtuse.svg Тупоугольный	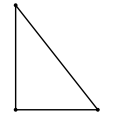Прямоугольный
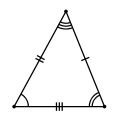Разносторонний	Файл:Triangle-isosceles.svg Равнобедренный	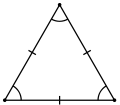Равносторонний

По величине углов

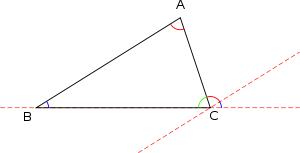
Поскольку в евклидовой геометрии сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше. Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.

По числу равных сторон

Определения, связанные с треугольником

Все факты, изложенные в этом разделе, из евклидовой геометрии.

Лучи, отрезки и точки

В равнобедренном треугольнике медиана, высота и биссектриса, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный. Если треугольник разносторонний, то для любой его вершины биссектриса, проведённая из неё, лежит между медианой и высотой, проведёнными из той же вершины.

Чевианы, лежащие на прямых, симметричных медианам относительно биссектрис, называются симедианами. Они проходят через одну точку — точку Лемуана.

Некоторые точки в треугольнике — «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли. Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это — точки Аполлония. Точки и такие, что и называются точками Брокара.

Прямые

В любом треугольнике центр тяжести, ортоцентр и центр описанной окружности лежат на одной прямой, называемой прямой Эйлера.

Прямая, проходящая через центр описанной окружности и точку Лемуана, называется осью Брокара. На ней лежат точки Аполлония. Также на одной прямой лежат точки Торричелли и точка Лемуана. Основания внешних биссектрис углов треугольника лежат на одной прямой, называемой осью внешних биссектрис. На одной прямой лежат также точки пересечения прямых, содержащих стороны ортотреугольника, с прямыми, содержащими стороны треугольника. Эта прямая называется ортоцентрической осью, она перпендикулярна прямой Эйлера.

Если на описанной окружности треугольника взять точку, то её проекции на стороны треугольника будут лежать на одной прямой, называемой прямой Симсона данной точки. Прямые Симсона диаметрально противоположных точек перпендикулярны.

Треугольники

Окружности

Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек или окружностью Эйлера. Центр окружности девяти точек лежит на прямой Эйлера. Окружность девяти точек касается вписанной окружности и трёх вневписанных. Точка касания вписанной окружности и окружности девяти точек называется точкой Фейербаха. Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, ортезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности — окружности Конвея. В любой треугольник можно вписать три окружности таким образом, что каждая из них касается двух сторон треугольника и двух других окружностей. Такие окружности называются окружностями Мальфатти. Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна.

В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера. Отрезки, соединяющие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.

Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна, а отрезки, соединяющие вершины с точками касания вневписанных окружностей — в точке Нагеля.

Эллипсы, параболы и гиперболы

В треугольник можно вписать бесконечно много коник (эллипсов, парабол или гипербол). Если в треугольник вписать произвольную конику и соединить точки касания с противоположными вершинами, то получившиеся прямые пересекутся в одной точке, называемой перспектором коники. Для любой точки плоскости, не лежащей на стороне или на её продолжении существует вписанная коника с перспектором в этой точке. [1]

В треугольник можно вписать эллипс, который касается сторон в серединах. Такой эллипс называется вписанным эллипсом Штейнера (его перспектором будет центроид треугольника). [2] Описанный эллипс, который касается прямых, проходящих через вершины параллельно сторонам, называется описанным эллипсом Штейнера. Если аффинным преобразованием («перекосом») перевести треугольник в правильный, то его вписанный и описанный эллипс Штейнера перейдут во вписанную и описанную окружности. Чевианы, проведённые через фокусы описанного эллипса Штейнера (точки Скутина), равны (теорема Скутина). Изо всех описанных эллипсов описанный эллипс Штейнера имеет наименьшую площадь, а изо всех вписанных наибольшую площадь имеет вписанный эллипс Штейнера. [3]

Эллипс с фокусами в точках Брокара называется эллипсом Брокара. Его перспектором служит точка Лемуана. [4]

Перспекторы вписанных парабол лежат на описанном эллипсе Штейнера. [5] Фокус вписанной параболы лежит на описанной окружности, а директриса проходит через ортоцентр. [6] Парабола, вписанная в треугольник, имеющая директрисой прямую Эйлера, называется параболой Киперта. Её перспектор — четвёртая точка пересечения описанной окружности и описанного эллипса Штейнера, называемая точкой Штейнера.

Если описанная гипербола проходит через точку пересечения высот, то она равносторонняя (то есть её асимптоты перпендикулярны). [7] Точка пересечения асимптот равносторонней гиперболы лежит на окружности девяти точек. [7]

Преобразования

Если прямые, проходящие через вершины и некоторую точку, не лежащую на сторонах и их продолжениях, отразить относительно соответствующих биссектрис, то их образы также пересекутся в одной точке, которая называется изогонально сопряжённой исходной (если точка лежала на описанной окружности, то получившиеся прямые будут параллельны). Изогонально сопряжёнными являются многие пары замечательных точек: центр описанной окружности и ортоцентр, центроид и точка Лемуана, точки Брокара. Точки Аполлония изогонально сопряжены точкам Торричелли, а центр вписанной окружности изогонально сопряжён сам себе. Под действием изогонального сопряжения прямые переходят в описанные коники, а описанные коники — в прямые. Так, изогонально сопряжены гипербола Киперта и ось Брокара, гипербола Енжабека и прямая Эйлера, гипербола Фейербаха и линия центров вписанной о описанной окружностей. Описанные окружности подерных треугольников изогонально сопряжённых точек совпадают. Фокусы вписанных эллипсов изогонально сопряжены.

Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением. Оно также переводит прямые в описанные коники. Изотомически сопряжены точки Жергонна и Нагеля. При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в бесконечно удалённую прямую перейдёт описанный эллипс Штейнера.

Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием. Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция — проективное преобразование, которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.

Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной полярой исходной точки. Ортоцентрическая ось — трилинейная поляра ортоцентра; трилинейной полярой центра вписанной окружности служит ось внешних биссектрис. Трилинейные поляры точек, лежищих на описанной конике, пересекаются в одной точке (для описанной окружности это точка Лемуана, для описанного эллипса Штейнера — центроид). Композиция изогонального (или изотомического) сопряжения и трилинейной поляры является преобразованием двойственности (если точка, изогонально (изотомически) сопряжённая точке , лежит на трилинейной поляре точки , то трилинейная поляра точки, изогонально (изотомически) сопряжённой точке лежит на трилинейной поляре точки ).

Кубики

Кубика — это кривая третьего порядка (задающаяся уравнением третьей степени). Многие замечательные кубики, связанные с треугольником, строятся следующим образом: фиксируется точка в плоскости (возможно, бесконечно удалённая). Тогда множество таких точек , что прямая проходит через эту точку, является описанной около треугольника кубикой (здесь — точка, изогонально сопряжённая ). Такие кубики проходят также через центры вписанной и вневписанных окружностей, а также через саму фиксированную точку и изогонально сопряжённую ей. [10]

Соотношения в треугольнике

Примечание: в данном разделе , , — это длины трёх сторон треугольника, и , , — это углы, лежащие соответственно напротив этих трёх сторон (противолежащие углы).

Неравенство треугольника

В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном — равна. Иначе говоря, длины сторон треугольника связаны следующими неравенствами:

Неравенство треугольника является одной из аксиом метрики.

Теорема о сумме углов треугольника

Теорема синусов

где R — радиус окружности, описанной вокруг треугольника. Из теоремы следует, что если a Теорема косинусов

Источник

Частица как часть речи

Частица — это слу­жеб­ная часть речи, кото­рая при­да­ет смыс­ло­вые оттен­ки сло­вам и пред­ло­же­ни­ям, а так­же упо­треб­ля­ет­ся для обра­зо­ва­ния форм слов.

Определим, что такое части­ца как часть речи в рус­ском язы­ке. Выясним, что выра­жа­ет части­ца, для чего исполь­зу­ет­ся в речи, каки­ми обла­да­ет признаками.

Частица — это служебная часть речи

По сво­им зна­че­ни­ям, грам­ма­ти­че­ским при­зна­кам и син­так­си­че­ской функ­ции в пред­ло­же­нии сло­ва рус­ско­го язы­ка делят­ся на груп­пы, лексико-семантические раз­ря­ды, кото­рые назы­ва­ют­ся частя­ми речи.

В рус­ском язы­ке раз­ли­ча­ют само­сто­я­тель­ные и слу­жеб­ные части речи. Слова само­сто­я­тель­ных частей речи име­ют опре­де­лен­ное зна­че­ние (назы­ва­ют пред­мет, при­знак, дей­ствие и пр.), высту­па­ют в роли глав­ных или вто­ро­сте­пен­ных чле­нов пред­ло­же­ния, могут пояс­нять­ся дру­ги­ми частя­ми речи (весе­лый маль­чик, очень весе­лый маль­чик).

Служебные части речи, напро­тив, не обо­зна­ча­ют явле­ний дей­стви­тель­но­сти и их при­зна­ки, а толь­ко выпол­ня­ют опре­де­лен­ную функ­цию в сло­во­со­че­та­нии и предложении.

В рус­ском язы­ке выде­ля­ют три слу­жеб­ные части речи:

Служебные сло­ва не име­ют лек­си­че­ско­го зна­че­ния, не явля­ют­ся чле­на­ми пред­ло­же­ния, но могут вхо­дить в их состав. Их при­зна­ком явля­ет­ся неиз­ме­ня­е­мость. К слу­жеб­ным частям речи нель­зя задать вопрос.

Отличия частиц от других частей речи

Чем же отли­ча­ет­ся части­ца как слу­жеб­ная часть речи от пред­ло­га и сою­за? У каж­дой слу­жеб­ной части речи суще­ству­ет своя функ­ция в связ­ной речи.

Предлог выра­жа­ет отно­ше­ния меж­ду само­сто­я­тель­ны­ми сло­ва­ми в сло­во­со­че­та­нии и пред­ло­же­нии (пой­ду в сад, обой­дем­ся без него).

Союз — это сред­ство свя­зи меж­ду отдель­ны­ми сло­ва­ми (одно­род­ны­ми чле­на­ми пред­ло­же­ния) и частя­ми слож­ных предложений.

А части­ца как слу­жеб­ная часть речи вно­сит раз­лич­ные смыс­ло­вые оттен­ки в выска­зы­ва­ние, слу­жит для пере­да­чи субъ­ек­тив­но­го отно­ше­ния гово­ря­ще­го к тому, о чем идет речь. Чтобы убе­дить­ся в этом, выра­зи­тель­но про­чтем неболь­шой текст:

В без­лун­ную ночь посмот­рим на небо. Как мно­го звезд на чер­ном бар­хат­ном поло­ге! Разве звез­дам не тес­но там? Вот стре­ми­тель­но летит звез­доч­ка вниз. Куда же она упа­дёт? Неужели сго­рит, не доле­тев до Земли? Звезд ста­ло мень­ше. Надо бы их пересчитать.

Во вто­ром пред­ло­же­нии с помо­щью сло­ва «как» созда­ет­ся настро­е­ние удив­ле­ния и вос­хи­ще­ния ( как мно­го звезд…), что пере­да­ет­ся с помо­щью этой части­цы и вос­кли­ца­тель­ной инто­на­ции. В сле­ду­ю­щем пред­ло­же­нии сло­во «раз­ве» помо­га­ет создать вопрос. А части­ца «вот» ука­зы­ва­ет на летя­щую звездочку.

Уберем выде­лен­ные сло­ва из это­го выска­зы­ва­ния. Что про­изо­шло? Текст поте­рял свою «изю­мин­ку» — выра­зи­тель­ность и экс­прес­сив­ность, кото­рую ему при­да­ва­ли части­цы. Из опи­са­ния ноч­но­го звезд­но­го неба исчез­ла часть кра­сок, с помо­щью кото­рых созда­ет­ся эмо­ци­о­наль­ный фон тек­ста и пере­да­ет­ся отно­ше­ние авто­ра к кра­со­те природы.

Частицы — это спе­ци­аль­ные сред­ства речи для пере­да­чи раз­лич­ных чувств в выска­зы­ва­нии. Но кро­ме этой функ­ции неко­то­рые части­цы помо­га­ют созда­вать грам­ма­ти­че­ские фор­мы слов (отве­тил бы мне) и даже обра­зу­ют новые сло­ва (что-то, куда-либо).

Разряды частиц

В свя­зи со зна­че­ни­ем и функ­ци­ей в пред­ло­же­нии части­цы делят на три группы:

Она хоте­ла бы напить­ся коло­дез­ной воды.

Образующие повели­тельное наклонениеда, давай, давай­те, пусть, пус­кай Пусть радост­ным будет твой день!ОтрицательныеНЕПолное отри­ца­ние при ска­зу­е­момТы не слы­шишь меня.Частичное — при дру­гих чле­нах предложенияНе вам судить об этом.Утверждение в воскли­цательных и вопроси­тельных предложенияхЧего толь­ко не уви­дишь здесь!

Кто не зна­ет Юрия Гагарина?

В устой­чи­вых сочетанияхедва не, чуть не, вовсе неПри двой­ном отрицанииНе можем не сооб­щить об этом (= дол­жны сооб­щить, обя­за­тель­но сообщим)НИУсиление при отрица­нии с «не»Я не ска­жу боль­ше ни слова.Усиление утвер­жде­ния в при­да­точ­ных с уступи­тельным оттенкомКак ни труд­но, а выпол­ни это. (=хотя труд­но, выполни).

Формообразующие части­цы пусть, пус­кай, да, давай, давай­те, бы (б) упо­треб­ля­ют­ся при обра­зо­ва­нии форм пове­ли­тель­но­го и услов­но­го накло­не­ния глагола.

Пусть уйдут навсе­гда враж­да и ненависть!

Хотелось бы услы­шать ваше мнение.

Частица «не» обра­зу­ет новые сло­ва с про­ти­во­по­лож­ным значением:

Смысловые части­цы созда­ют допол­ни­тель­ные оттен­ки зна­че­ний у отдель­ных слов и у все­го пред­ло­же­ния цели­ком. Они могут выра­жать вос­хи­ще­ние, удив­ле­ние, сомне­ние, уточ­не­ние, отри­ца­ние и пр. эмо­ции говорящего.

Сравним:

Разве ты уже про­чи­тал эту кни­гу? (удив­ле­ние)

Вряд ли ты уже про­чи­тал эту кни­гу (сомне­ние).

Ты не про­чи­тал эту кни­гу (отри­ца­ние).

Признаки частицы

Как и дру­гие слу­жеб­ные части речи, пред­лог и союз, части­цы не изменяются.

По соста­ву они могут быть

1. про­сты­ми, состо­я­щи­ми из одно­го слова:

2. состав­ны­ми, скла­ды­ва­ю­щи­ми­ся из несколь­ких слов:

По про­ис­хож­де­нию различают

1. непро­из­вод­ные частицы:

2. про­из­вод­ные от слов дру­гих частей речи:

Морфологический разбор частицы

Примеры

На горе сто­ит церк­вуш­ка, и как раз вни­зу бьет родник.

Как раз — это части­ца, неиз­ме­ня­е­мая, уточняющая.

Нас этим фоку­сом вряд ли удивишь.

Вряд ли — части­ца, неиз­ме­ня­е­мая, выра­жа­ю­щая сомнение.

Стало так страш­но, что про­сто серд­це замерло.

Просто — части­ца, неиз­ме­ня­е­мая, усилительная.

Видеоурок

Источник