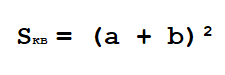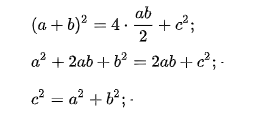Что вам нужно для теоремы пифагора
Теорема Пифагора: история, формулы и доказательства
Теорема Пифагора – одна из самых известных геометрических теорем, которая устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Большинство ученых считают, что теорема Пифагора была доказана древнегреческим математиком и философом Пифагором (или Питагором). Однако есть версия, что теорему знали и до его рождения. Доказательством этого является то, что в Древнем Египте знали, что треугольник, у которого стороны имеют 3 см, 4 см и 5 см, является прямоугольным. А о других теоремах можно узнать в учебнике по геометрии за 8 класс А.Г. Мерзляка.
Еще в детстве Пифагор отличился интересом к точным наукам. Впоследствии он переехал жить на остров Лесбос, где познакомился с Фалесом Милетским – древнегреческим философом и математиком, который доказал теоремы о трех точках на окружности и пропорциональных отрезках. За время, когда Пифагор учился в Милетской школе, он изучал астрологию, медицину, прогнозы затмений и другие важные в то время науки. Лекции Фалеса и его ученика Анаксимандра сыграли важную роль для Пифагора.
После обучения в Египте, плена в Вавилоне, в 60 лет Пифагор решает вернуться домой, чтобы поделиться своими знаниями с народом. Впоследствии он открыл собственную школу, в которой геометрия впервые выступает как самостоятельная наука.
О том, что квадрат гипотенузы равен сумме квадратов катетов, знали задолго до рождения Пифагора. Но именно он считается первым ученым, который доказал соотношение сторон треугольника.
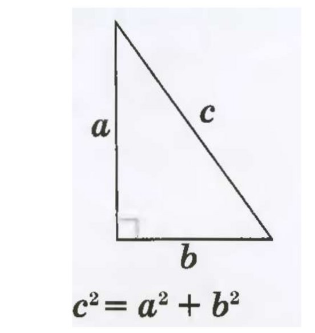
В теореме Пифагора говорится, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пусть ВС = а; АС = b; АВ = с.
Тогда имеем такую формулу, которая применяется при нахождении неизвестной стороны в прямоугольном треугольнике, когда две другие – известны:
Когда мы определили квадрат гипотенузы, нужно найти квадратный корень. Такую же формулу мы можем применить к неизвестному катету:
А больше рисунков и формул можно увидеть в онлайн уроке за 8 класс по геометрии на тему «Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора».
Самый популярный и самый простой метод доказательства теоремы связан с площадями фигуры.
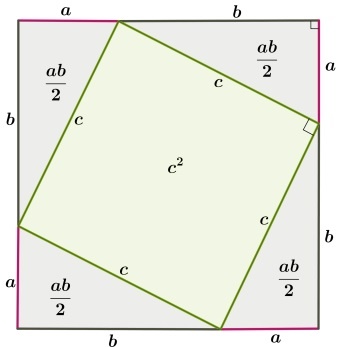
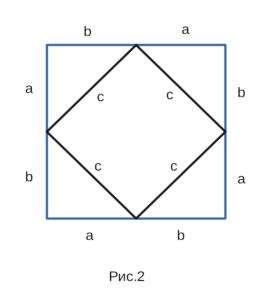
Нужно расположить одинаковые прямоугольные треугольники так, чтобы внутри образовался квадрат. Каждая сторона внешнего квадрата должна состоять из суммы катетов прямоугольного треугольника a + b.
Площадь этого квадрата можно будет найти благодаря формуле:
Внутренний четырехугольник можно считать квадратом, ведь, если добавить два острые углы прямоугольного треугольника, то получится 90°. Следует считать, что площадь внешнего квадрата состоит из площади внутреннего квадрата и четырех площадей одинаковых прямоугольных треугольников. Итак, в заключении:
Итак, теорема Пифагора доказана.
2. Доказательство Евклида
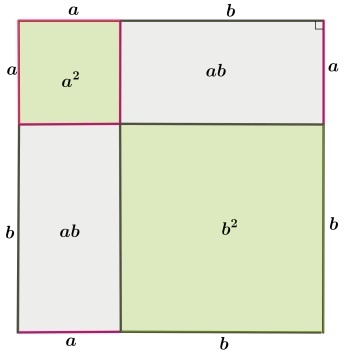
Доказательство Евклида также называется «Пифагоровы штаны». Ее так назвали, потому что сумма площади квадратов, образованных с использованием катетов прямоугольного треугольника равна площади квадрата, который построен на гипотенузе этого же треугольника. Квадраты напоминали ученикам мужские штаны.
На примере приведенных картинок ниже можно увидеть, как оригинально передали суть доказательства Евклида.
В вашем учебнике не было таких доказательств? Вы можете найти другой в разделе «Учебники по геометрии за 8 класс».
Пример задачи на применение теоремы Пифагора
Условия задачи. В треугольнике ABC дано: ∠C = 90 °, BC = 20 см, AC = 15 см. Найти сторону AB.
Решение. Поскольку в треугольнике АВС ∠С = 90°, следовательно, по теореме Пифагора имеем:
АВ² = BС² + АС²; AВ² = 20² + 15², AВ² = 625, AB = √625| AB = 25 см.
Если вам нужно решить задачу с помощью теоремы Пифагора, а вы сомневаетесь в конечном ответе, тогда можете проверить свои знания благодаря разделу «ГДЗ и решебники по геометрии за 8 класс».
А если вы хотите крепче закрепить знания по другим темам по геометрии, то можете просматривать видео в разделе «Онлайн уроки за 8 класс по геометрии». Узнайте больше о перпендикуляре и наклонной, сумме углов выпуклого треугольника, площадь квадрата и прямоугольника, решение задач методом площадей и тому подобное.
Теорема Пифагора
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ∆ABC, в котором ∠C = 90º.
Пошаговое доказательство:
a 2 + b 2 = c * HB + c * AH
a 2 + b 2 = c * (HB + AH)
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?
Как решаем:
Пусть катеты a = 6 и b = 8.
Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.
Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?
Ответ: треугольник не является прямоугольным.
Доказательства теоремы Пифагора
Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.
Теорема Пифагора — краткая история
Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.
Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Формулировка теоремы
Изначальная (геометрическая) формулировка Пифагора гласила:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Позднее появился алгебраический вариант:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.
Уравнение
В виде формулы теорема Пифагора записывается следующим образом:
Доказательство через подобные треугольники
Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.
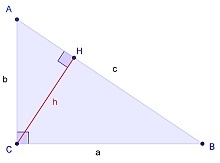
Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.
Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:
CB 2 =ABxHB, AC 2 =ABxAH
Сложив между собой квадраты катетов, получаем:
AC 2 +CB 2 =ABx(HB+AH)=AB 2
Это и требовалось доказать.
Другие способы доказательства теоремы
Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.
Методом площадей
Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.
Площадь внешнего квадрата включает в себя:
Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.
Методом бесконечных малых
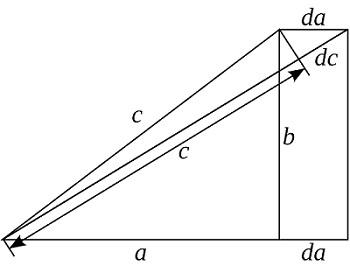
Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем
Разделяя переменные составляется дифференциальное уравнение:
Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:
определяя из начальных условий константу интегрирования, получим:
a = 0 ⇒ c 2 = b 2 = const
Таким образом мы определяем, что
Следствие из теоремы Пифагора
Его так же называют обратной теоремой Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.
В алгебраическом виде это можно представить так:
c2=a2+b2, где:
Применение теоремы
Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.
Расстояние между точками
Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:
Евклидова метрика
В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:
Теория чисел
Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.
Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.
Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.
Примеры решения задач
Задача 1
В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.
Решение
Для нахождения ответа подставим в формулу исходные значения:
Задача 2
Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.
Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:
Задача 3.
Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.
Решение
Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.
Применение теоремы Пифагора в повседневной жизни
Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.
Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:
Видео
Примеры задач
Задание 1В прямоугольном треугольнике один катет равен 3 см, другой – 4 см. Найдите длину его гипотенузы.
Задание 2Один из катетов прямоугольного треугольника равняется 6 см, а гипотенуза – 10 см. Найдите длину второго катета.
Вычисление расстояния между двумя точками на координатной плоскости
Выберите две точки на координатной плоскости. По теореме Пифагора можно вычислить длину отрезка, соединяющего две точки на координатной прямой. Для этого необходимо знать координаты (х,у) каждой точки. Чтобы найти расстояние между двумя точками, вы будете рассматривать точки в качестве вершин треугольника, не прилежащих к прямому углу прямоугольного треугольника. Таким образом, вы сможете легко найти катеты треугольника, а затем вычислить гипотенузу, которая равна расстоянию между двумя точками.
Нанесите точки на координатную плоскость. Отложите координаты (х,у), где координата «х» откладывается по горизонтальной оси, а «у» — по вертикальной. Вы можете найти расстояние между точками без построения графика, но график позволяет визуально представить процесс ваших вычислений.
Используйте теорему Пифагора для нахождения гипотенузы. Расстояние между двумя точками равно гипотенузе треугольника, две стороны которого вы только что нашли. Используйте теорему Пифагора, чтобы найти гипотенузу, подставив в формулу найденные значения катетов (a и b). В нашем примере а = 3 и b = 4. Гипотенуза вычисляется следующим образом: (3)²+(4)²= c² c= √(9+16) c= √(25) c= 5. Расстояние между точками А(6,1) и В(3,5) равно 5.
Интуитивное понимание теоремы Пифагора
Никто не спорит с тем, что теорема Пифагора работает. Но почти все её доказательства основаны на механических действиях: переставляем местами фигуры, и вуаля! — уравнение всё равно работает. Давайте подумаем: вам правда интуитивно понятно, что уравнение должно выглядеть как a² + b² = c²? А почему не 2a² + b² = c²? Давайте попробуем найти в этом смысл.
Для начала нам понадобится осознать и принять удивительный факт: любой прямоугольный треугольник можно разбить на два подобных прямоугольных треугольника.
Круто, да? Всего один опущенный перпендикуляр, и один треугольник превращается в две свои маленькие копии.
Собственно, этот пример говорит нам об очень простой вещи:
Площадь (чего-то большого) = Площадь (кое-чего среднего) + Площадь (кое-чего поменьше)
Маленькие треугольники были получены из большого, поэтому мы просто складываем их площади. И да, самое главное: поскольку треугольники подобны, для них действует одна и та же формула вычисления площади.
Давайте назовём длинную сторону (с длиной 5) — с, среднюю сторону (с длиной 4) — b, и короткую сторону (с длиной 3) — a. Формула площади для этих треугольников выглядит так:
Площадь = F*гипотенуза²,
где F — это множитель (в этом случае — 6/25 или 0,24). С формулой можно поиграть:
Площадь (чего-то большого) = Площадь (кое-чего среднего) + Площадь (кое-чего поменьше)
Fc² = Fb² + Fa²
Просто уберите F, и вы получите:
c² = b² + a²
Ой, так это же наша любимая теорема! Мы знали, что она нас не подведёт, но теперь мы понимаем, почему:
Конечно, теорема Пифагора работает только в Евклидовой геометрии и не может применяться, например, к сферам. Но об этом нужно поговорить в другой раз.
Теорема Пифагора, формула
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов () равна квадрату гипотенузы (). Это одна из основополагающих теорем эвклидовой геометрии. Формула:
Как уже говорилось, есть много разнообразных доказательств теоремы с разносторонними математическими подходами. Однако, более часто используют теоремы, связанные с площадями.
То есть сумма площадей квадратов, построенных на катетах равняется площади квадрата, построенном на гипотенузе. Соответственно, площади этих квадратов равны – 
Попробуйте сами
В теорему Пифагора можно подставлять абсолютно любые цифры. Она может помочь нам и в повседневной жизни. Например, мы никак не можем выбрать: заказать большую пиццу диаметром 50 см или две диаметром 30 см? Мы с теоремой уже знакомы хорошо и нас не обмануть: площадь одной пиццы в 50 см будет действительно больше, чем площадь двух пицц по 30 см в диаметре (можете проверить, мы не обманываем). Всегда можно подставить другие цифры, а для ленивых есть простой и удобный калькулятор.
Теорема Пифагора
Теорема Пифагора является одной из важнейших теорем в геометрии.
Формулировка у теоремы такая:
в прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.
Зная формулировку теоремы Пифагора и две стороны прямоугольного треугольника:
два катета либо катет и гипотенузу, можно найти третью сторону треугольника,
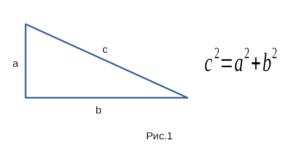
соответственно: гипотенузу либо катет. На рисунке 1 изображен
прямоугольный треугольник и формулировка теорема Пифагора.
Доказательство теоремы Пифагора
Для доказательства этой теоремы, нарисуем прямоугольный треугольник.
Ради удобства обозначим гипотенузу латинской буквой с, а катеты латинскими
буквами a и b. Докажем, что в прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов, или иначе \( c^2=a^2+b^2 \).
Теорема доказана.
Следствия из теоремы Пифагора
У этой теоремы много следствий, которые используются при доказательстве
других теорем и некоторых свойств. Перечислим основные из них: