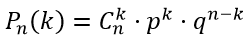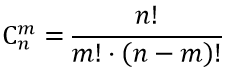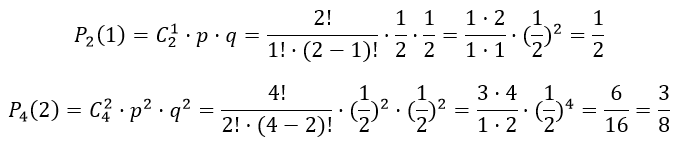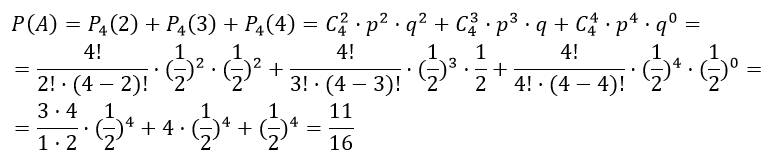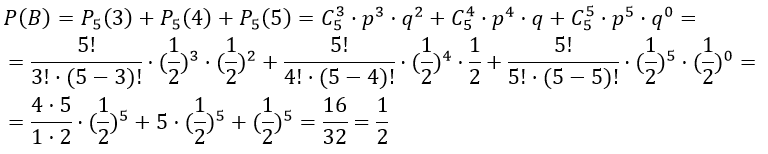Что вероятнее выиграть у равносильного противника
Решение задач про шахматные партии
Чаще всего в задаче про партии следует вычислить две вероятности и сравнить:
Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть 2 партии из 4 или 3 партии из 6 (ничьи во внимание не принимаются).
Видеоурок и шаблон Excel
Посмотрите наш ролик о решении задач об играх и партиях: как использовать Excel для решения типовых задач с игроками и партиями (как для малого, так и для большого числа партий).
Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.
Примеры решений задач о шахматных партиях
Рассмотрим несколько типовых примеров.
Пример 1. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть 2 партии из 4 или 3 партии из 6 (ничьи во внимание не принимаются).
Пример 2. Играет два равных по силе игрока, какая вероятность выше: выиграть одну партию из трех, или три из пяти.
Пример 3. Играют равносильные противники. Что вероятнее: выиграть не менее трех партий из четырех или не менее шести из восьми? (Ничьи не учитываются)
В отличие от предыдущих задач, здесь нужно найти вероятность того, что число выигрышных партий будет находится в некотором интервале (а не равно в точности какому-то числу). Но формула используется по-прежнему таже самая.
Найдем вероятность выиграть не менее трех партий из четырех, то есть вероятность выиграть или три партии, или четыре партии. Данные вероятности равны по формуле (1):
Аналогично находим вторую вероятность выиграть не менее 6 партий из 8 (то есть выиграть или 6, или 7, или 8 партий). В этот раз все вычисления запишем сразу в одну формулу:
Итак, вероятнее выиграть не менее 3 партий из 4 (так как 0,3125 больше чем 0,145).
Пример 4. Какова вероятность, что игрок, который слабее своего оппонента в два раза выиграет две партии из трех
Для полноты изложения приведу решение этой задачи, с первого взгляда она похожа на предыдущие (и так и есть, конечно), но есть некоторое отличие. А именно, противники тут не равносильные, а один слабее другого. С точки зрения формализации задачи, это будет означать, что вероятность выигрыша для игрока равна не 0,5, а другому числу. Какому?
Решение типовых задач. Пример 7.1. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен):
Пример 7.1. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен):
а) три партии из четырех или пять из восьми;
б) не менее трех партий из четырех или не менее пяти партий из восьми?
Так как противники равносильные, то вероятности выигрыша и проигрыша каждой партии одинаковы и равны p = q = l/2.
а) Вероятность выиграть три партии из четырех
Вероятность выиграть пять партий из восьми
.
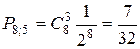
Так как 
, то вероятнее выиграть три партии из четырех.
б) Вероятность выиграть не менее трех партий из четырех
,
а вероятность выиграть не менее пяти партий из восьми
.
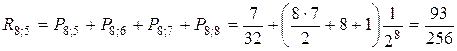
Так как 
, то вероятнее выиграть не менее пяти партий из восьми.
Пример 7.2. Имеется шесть потребителей электрического тока, для первого из которых при определенных условиях вероятность того, что произойдет авария, приводящая к отключению потребителя, равна 0,6, для второго — 0,2, а для четырех остальных — по 0,3. Определить вероятность того, что генератор тока будет отключен полностью:
а) если все потребители соединены последовательно;
б) если потребители соединены так, как показано на схеме (рис. 6).
а) Вероятность неотключения всех шести потребителей равна произведению вероятностей неотключения каждого потребителя, т. е.
.
Искомая вероятность равна вероятности отключения хотя бы одного потребителя, т. е.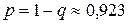 
.
б) В этом случае генератор будет отключен полностью, если в каждой паре последовательно соединенных потребителей отключен хотя бы один потребитель:
.
Пример 7.3. Большая партия изделий содержит один процент брака. Каков должен быть объем случайной выборки, чтобы вероятность встретить в ней хотя бы одно бракованное изделие была не меньше 0,95?
Искомое число n находится по формуле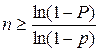 
.
В данном случае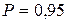 
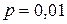
, а 
. Поэтому 
.
Пример 7.4. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0,4 независимо от заявок других магазинов. Найти наивероятнейшее число заявок в день и вероятность получения этого числа заявок.
В данном случае n = 10, p = 0,4, (n + 1)p = 4,4. Наивероятнейшеё число 
, заявок равно целой части числа (n + 1)p, т. е. p = 4.
Вероятность четырёх заявок из десяти
.
Дата добавления: 2014-12-23 ; просмотров: 211 ; Нарушение авторских прав
Что вероятнее выиграть у равносильного противника три партии из четырех или пять из восьми?
 |  | Высшая математика |
 |  | Решение задачи |
 |  | 18 февраля 2021 |
 |  | Выполнен, номер заказа №16189 |
 |  | Прошла проверку преподавателем МГУ |
 |  | 137 руб. |
Напишите мне в whatsapp, пришлите ссылку на эту страницу в чат, оплатите и получите файл!
Закажите у меня новую работу, просто написав мне в whatsapp!
Похожие готовые решения по высшей математике: При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. Схема Бернулли
Условия, приводящие к формуле Бернулли, называются схемой повторных независимых испытаний или схемой Бернулли. Так как вероятности Рn(k) для различных значений k представляют собой слагаемые в разложении бинома Ньютона то распределение вероятностей Рn(k), где 0£k£n, называется биномиальным. При решении задач на использование формулы Бернулли часто применяют следующие формулы. Вероятность наступления события А: д) хотя бы один раз Пример 1. Что вероятнее: выиграть у равносильного противника (ничейный исход партии исключен) три партии из четырех или пять из восьми? Решение. Так как противники равносильны, то вероятность успеха (выиграть партию) равна Следовательно, выигрыш трех партий из четырех вероятнее, чем пять партий из восьми. Пример 2. Всхожесть семян данного сорта оценена вероятностью р=0,8. Каковы вероятности того, что из 5 семян войдет: 0, 1, 2, 3, 4, 5. Решение. Число опытов равно 5, опыты независимые. Вероятность появления события А (взошло семя) в каждом опыте одинакова и равна р=0,8, вероятность противоположного события q=0,2. Следовательно, можно воспользоваться формулой Бернулли. Из примера2 следует, что вероятность Pn(k) для данного n с увеличением m от 0 до 5 сначала возрастает, а затем уменьшается. Число k0, при котором Pn(k) имеет наибольшее значение, называется наивероятнейшим числом наступления успеха в n опытах. В приведенном примере k0=4. Наивероятнейшее число можно найти из неравенства Пример 3. Вероятность получения удачного результата при производстве сложного химического опыта равна 2/3. Найти наивероятнейшее число удачных опытов, если общее их число равно 7. Решение. Вероятность успеха в одном опыте Формулой Бернулли удобно пользоваться в том случае, когда число опытов n£10. При большом числе опытов по схеме Бернулли удобнее пользоваться приближенными формулами. Формула БернуллиЕсли в n испытаниях событие А случается (происходит) k раз и не случается (не происходит) (n-k) раз, то данную вероятность Рn(k) можно найти по формуле Бернулли: Пример 1 Пример 2 Каждый день акции компании X поднимаются в цене или падают в цене на один пункт с вероятностями 0,75 и 0,25. Найти вероятность того, что акции после 6 дней вернутся к своей первоначальной цене, то есть чтобы акции за это время 3 раза поднялись в цене и три раза опустились в цене. При этом изменения цены акции вверх и вниз – независимые события. Решение Пример 4
|
.
,
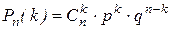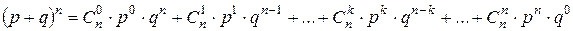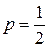, вероятность неудачи 
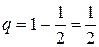. По формуле Бернулли находим
,
.
;
;
;
;
;
.
.
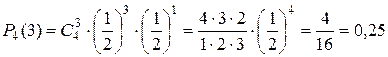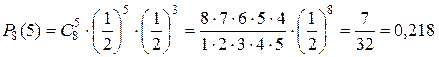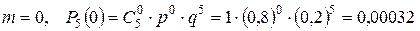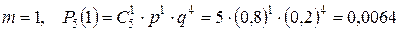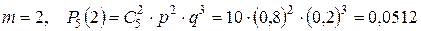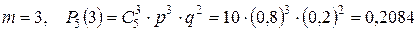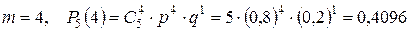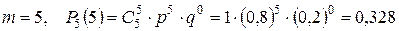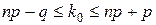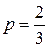, неудачи 
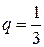, n = 7. Наивероятнейшее число удачных опытов k0 найдем из неравенства
;
;
.
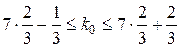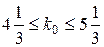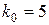