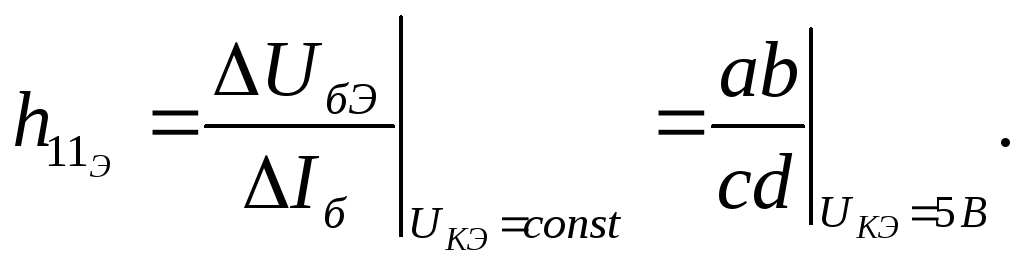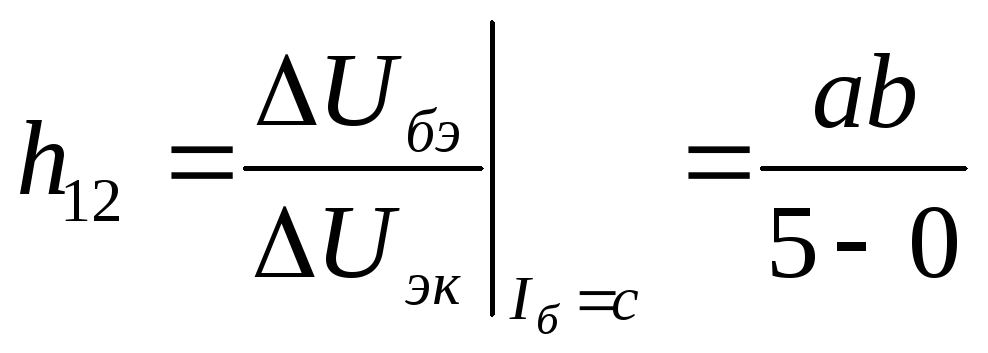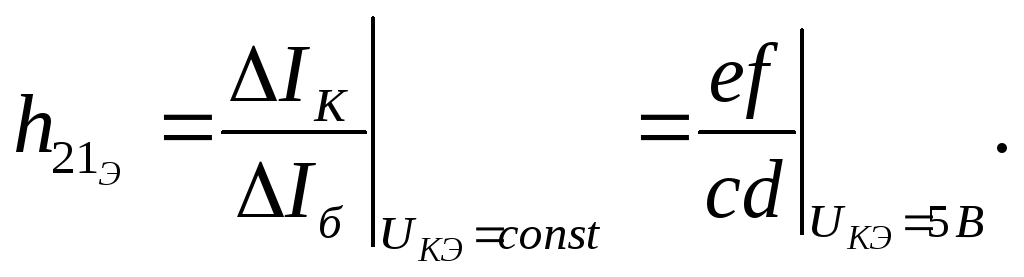что за такие h параметры и каким методом их проще определить

ОПРЕДЕЛЕНИЕ h- ПАРАМЕТРОВ БИПОЛЯРНЫХ ТРАНЗИСТОРОВ

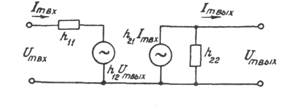
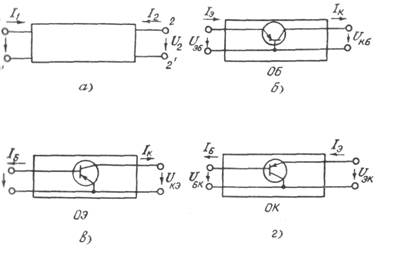
На практике часто пользуются вторичными параметрами транзисторов, характеризующими его как активный линейный четырехполюсник, т.е. прибор, имеющий два входных и два выходных зажима (рис.2.1). Вторичные параметры связывают друг с другом входные и выходные переменные токи и напряжения и справедливы только для данного режима транзистора и для малых амплитуд малых приращений тока и напряжения. Поэтому их называют низкочастотными малосигнальными параметрами.

Линейный четырехполюсник характеризуется двумя уравнениями, взаимно связывающими токи и напряжения на входе и выходе. Можно составить шесть пар таких уравнений, определяющих шесть различных систем параметров. В транзисторной технике наиболее широкое распространение получила система h-параметров.

Для малосигнальных параметров (для малых приращений токов и напряжений) систему (2.1) можно представить в линейном виде

Параметры h11 и h12 определяются из первого уравнения системы (2.2).

Полагая dUвых = 0, (Uвых = const), получим

— входное сопротивление транзистора для переменного входного тока (дифференциальное входное сопротивление) при постоянном напряжении на выходе (при отсутствии выходного переменного напряжения).

Полагая dIвх = 0, (Iвх = const) получим

— коэффициент обратной связи по напряжению.

Он показывает, какая доля выходного переменного напряжения передается на вход транзистора вследствие наличия в нем внутренней обратной связи. Условие Iвх = const в данном случае подчеркивает, что во входной цепи нет переменного тока. Следовательно, изменение напряжения на входе dUвх есть результат изменения только выходного напряжения dUвых.

Параметры h21 и h22 определяются из второго уравнения системы (2.2).

Полагая dUвых = 0 (Uвых = const), получим

коэффициент передачи тока (коэффициент усиления по току). Он показывает усиление переменного тока транзистором в режиме работы без нагрузки. УсловиеUвых = const, т.е. Rн = 0 задается для того, чтобы изменение выходного тока dIвх зависело от изменения входного тока dIвх. Именно при выполнении такого условия параметр h21 будет действительно характеризовать усиление тока самим транзистором. Если бы выходное напряжение менялось, то оно влияло бы на выходной ток, и по изменению этого тока нельзя уже было бы правильно оценить усиление.

Определить параметры можно не только через приращения токов и напряжений, но и через амплитуды (или действующие значения) переменных токов и напряжений из следующих уравнений:

Напомним, что h-параметры определены для малых амплитуд поэтому использование их для больших амплитуд дает значительные погрешности.

Уравнениям (2.12)-(2.16) соответствует эквивалентная схема, изображенная на рис.2.2

В ней генератор ЭДС h12Um.вых показывает наличие напряжения связи во входной цепи. Сам генератор надо считать идеальным, т.е. не имеющим внутреннего сопротивления. Генератор тока h21Im.вх в выходной цепи учитывает эффект усиления тока, а h22 является внутренней проводимостью. Хотя входная и выходная цепи кажутся не связанными друг с другом, на самом деле эквивалентные генераторы учитывают взаимосвязь этих цепей.

Источник

1.2. Методика графического определения h –параметров транзистора

Располагая вольт–амперными характеристиками транзистора, можно графическим путем определить низкочастотные значения h-параметров.

Рис.8.3. Входная характеристики транзистора в схеме с ОЭ.

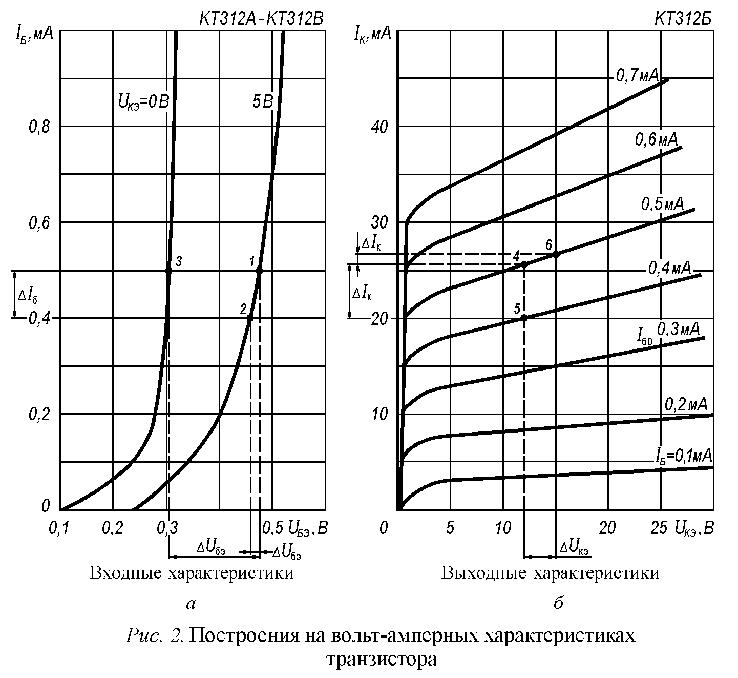
Вблизи рабочей точки А₁ выбираем вспомогательную точку А₂ с координатами по току I_б2 =c = d+I_б и по напряжения U_бэ2=b=a+U_бэ рис.8.3. Отсюда следует, что ΔI_б = cd, a U_бэ = ab_, тогда входное дифференциальное сопротивление h_11э, рассчитаем по формуле:

Приращения U_бэ и I_б выбирают так, чтобы не выходить за пределы линейного участка, их можно примерно принять за (10-20)% от значения U_бэ = а рабочей точки.

Графическое определение коэффициента обратной связи по напряжению

h_12э = U_бэ /U_кэI_б =const на входной характеристике (рис.8.3.) осуществляется по формуле

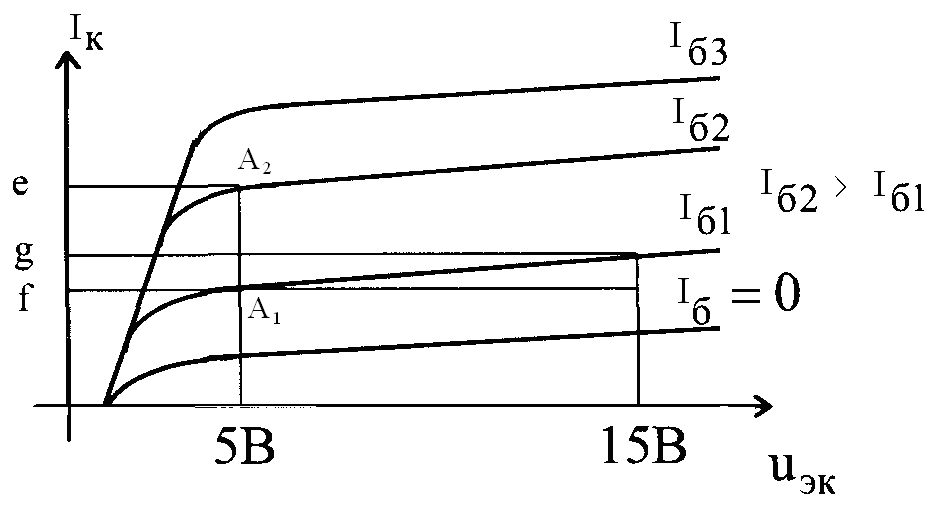
Рис.8.4. Выходная характеристики транзистора в схеме с ОЭ.

Параметры коэффициента усиления транзистора по току h_21э и выходной проводимости h_22э определяются из семейства выходных характеристик транзистора I_к=₁ (U_кэ) (рис.8.4).

2. Задания на теоретические расчеты

2.1. Ознакомьтесь со схемами включения биполярного транзистора, с методикой исследования и снятия статических вольт-амперных характеристик с ОЭ; с методикой графического определения h–параметров транзистора.

2.2. Рассчитайте по формуле (8.5) и постройте нагрузочную характеристику I_к= ₃ (U_кэ) биполярного транзистора для следующих исходных данных R_к=1кОм, 3кОм; Е_к=10B;

3. Задания на экспериментальное исследование и порядок их выполнения

Задание 1. Исследование статических вольтамперных характеристик (ВАХ) транзистора, включенного по схеме с ОЭ (с помощью амперметра-вольметра).

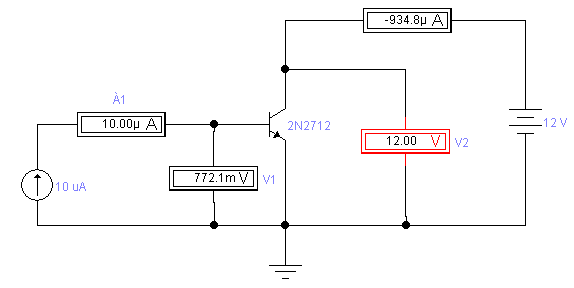
Рис.8.4. Схема измерения входной ВАХ биполярного транзистора, с помощью амперметра-вольтметра.

2.1. Снимите входную ВАХ – I_б=F(U_бэ)|_Uкэ=const для транзистора тип которого указан Вам преподавателем. Соберите схему (рис.8.4). Измерения проводите устанавливая значения I_б с помощью источника тока в мкА, при Uкэ=0 и +12В. При выполнении исследований следует учитывать, что параметры транзисторов могут существенно отличаться друг от друга, поэтому исходные данные тока I_б могут быть изменены студентом для того чтобы вид входной характеристики был примерно подобен графику представленному на рис. 8.3. Данные занесите в таблицу 8.1.

Источник

h-параметр транзистора: что это такое, формула, описание

При определении переменных составляющих токов и напряжений (т. е. при анализе на переменном токе) и при условии, что транзистор работает в активном режиме, его часто представляют в виде линейного четырехполюсника (рис. 1.81). В четырехполюснике условно изображен транзистор, включенный по схеме с общим эмиттером.

Для разных схем включения транзистора токи и напряжения этого-четырехполюсника обозначают различные токи и напряжения транзистора. Например, для схемы с общим эмиттером эти токи и напряжения следующие:

i₁ — переменная составляющая тока базы; u1— переменная составляющая напряжения между базой и эмиттером;

i₂ — переменная составляющая тока коллектора; u2— переменная составляющая напряжения между коллектором и эмиттером.

Транзистор удобно описывать, используя так называемые h-параметры. При этом

т. е. u1=h11·i1+h12·u2i1=h21·i1+h22·u2

Как легко заметить, коэффициент h₁₁ представляет собой входное сопротивление транзистора для переменного сигнала.

Аналогично h12=u1/u2|i1= 0h12 — коэффициент обратной связи по напряжению. Режим работы при i₁ = 0 называют холостым ходом на входе. Далее h21=i2/i1|u2= 0h21 — коэффициент передачи тока.

Параметры, соответствующие схеме с общим эмиттером, обозначают буквой «э», а схеме с общей базой — буквой «б».

Можно показать, что h₁₁э≈ rб+ (1 +β) · rэh₁₂э≈ rэ/ (2 · r′к)h₂₁≈βh22≈ 1/r′_к

Для создания математической модели транзистора полный набор h-параметров часто не требуется.

Источник

Что за такие h параметры и каким методом их проще определить

При определении переменных составляющих токов и напряжений (т. е. при анализе на переменном токе) и при условии, что транзистор работает в активном режиме, его часто представляют в виде линейного четырехполюсника (рис. 3.8). В четырехполюснике условно изображен транзистор с общим эмиттером.

Рис. 3.8. Транзистор в виде четырехполюсника

Для разных схем включения транзистора токи и напряжения этого четырехполюсника обозначают различные токи и напряжения транзистора. Например, для схемы с общим эмиттером эти токи и напряжения следующие:

i ₁ – переменная составляющая тока базы;

u ₁ – переменная составляющая напряжения между базой и эмиттером;

i ₂ – переменная составляющая тока коллектора;

u ₂ – переменная составляющая напряжения между коллектором и эмиттером.

Входное сопротивление транзистора для переменного сигнала (при закороченном выходе: u ₂ =0) :

Режим работы при i ₁ =0 называют холостым ходом на входе.

Источник

3. Расчетно-графическая работа «Определение h-параметров биполярного транзистора»

Определить h-параметры биполярного транзистора по его вольт-амперным характеристикам для заданной точки (U_к; I_б).

Вольт-амперные характеристики приведены в приложении 3.

Оформить работу в соответствии с требованиями приложения 1.

Варианты заданий РГР

«Определение h-параметров биполярного транзистора»

Коорд. точки для опред. h-параметров

Коорд. точки для опред. h-параметров

Методические указания к выполнению РГР

«Определение h-параметров биполярного транзистора»

Низкочастотные дифференциальные h-параметры транзистора, включенного по схеме с общим эмиттером, определяются по его вольт-амперным статическим характеристикам.

Параметры h_11э и h_12э определяют по входным характеристикам в соответствии с выражениями:

при ,

при ,

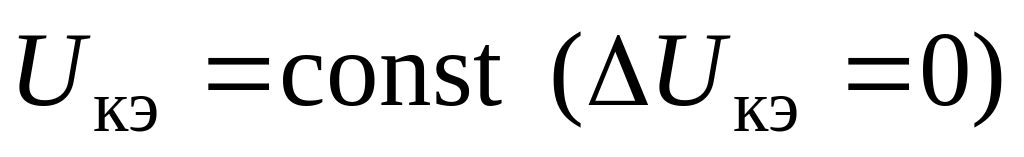
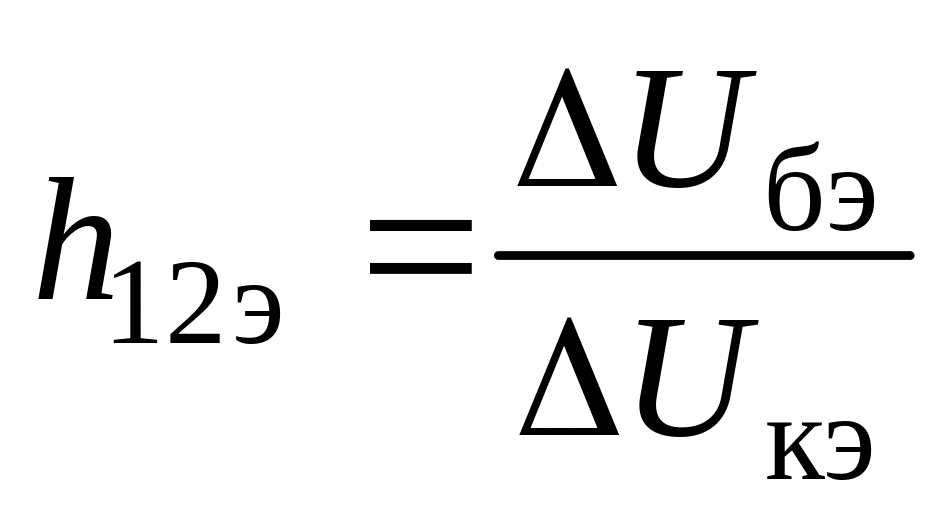
а параметры h_21э и h_22э – по выходным характеристикам в соответствии с выражениями:

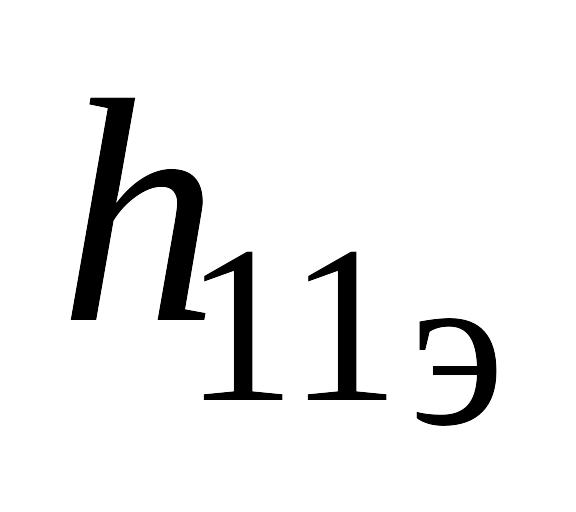
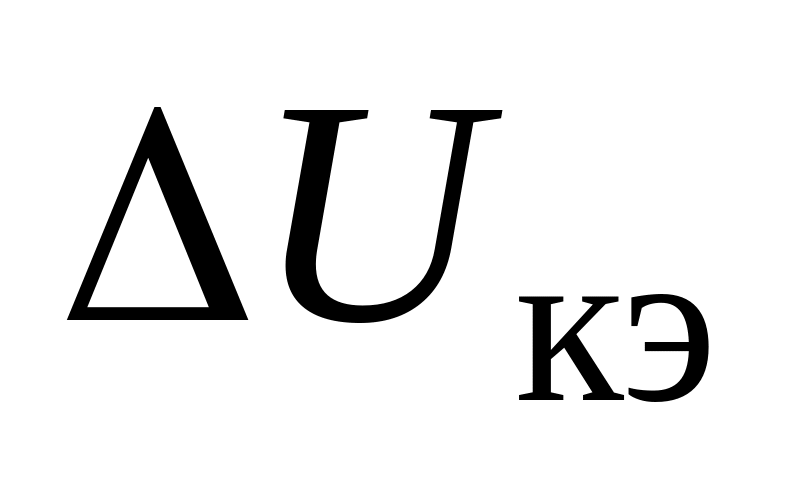
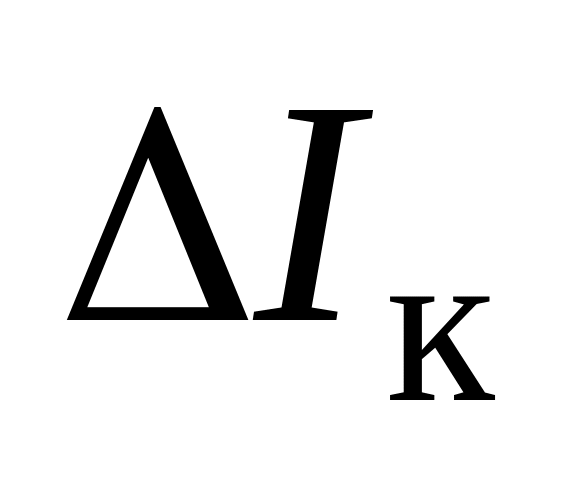
где – входное сопротивление биполярного транзистора; – безразмерный коэффициент внутренней обратной связи по напряжению; – безразмерный коэффициент передачи тока; – выходная проводимость биполярного транзистора; , , , – соответственно, приращения напряжения база–эмиттер и напряжения коллектор–эмиттер, тока базы и тока коллектора в области заданной точки (U_кэ; I_б) вольт-амперных характеристик биполярного транзистора.

Определение h-параметров транзистора по его вольт-амперным характеристикам показано на рис. 2 на примере транзистора КТ312Б для заданной точки с координатами (U_кэ = 12 В; I_б = 0,5 мА).

При выполнении работы исходные координаты заданной точки, в пределах которой следует определить h-параметры транзистора, допускается принять за данные одной из границ принимаемых интервалов приращений токов и напряжений, необходимых для расчета h-параметров.

Расчетные формулы для параметров h_11э и h_12э в этом случае имеют следующий вид:

,

.

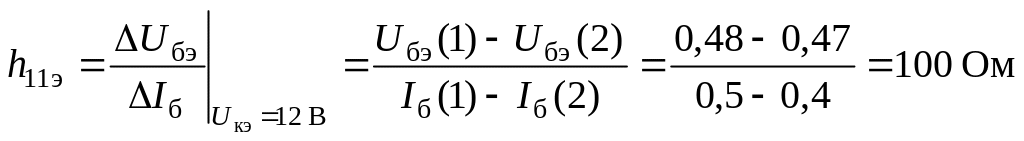
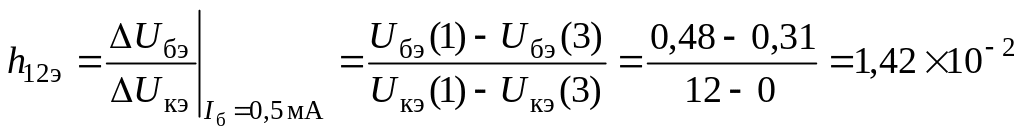
Расчетные формулы для параметров h_21э и h_22э имеют следующий вид:

,

.

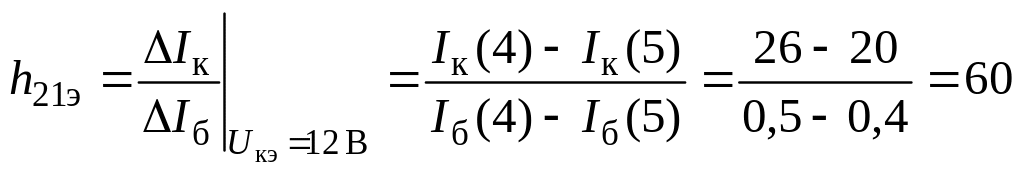
Таким образом, для точки с координатами U_кэ = 12 В; I_б = 0,5 мА транзистор КТ312Б имеет следующие значения h-параметров:

Источник