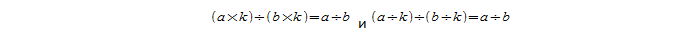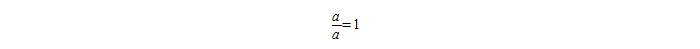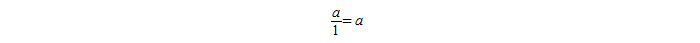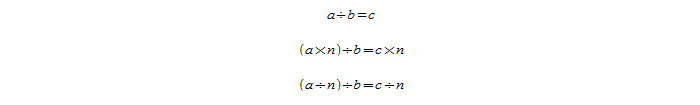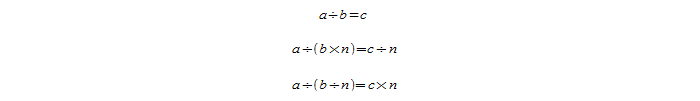что значит частное и произведение
Что такое сумма, разность, произведение, частное в математике?
В каких ещё значениях, не связанных с математикой, употребляются эти слова?
Я математик по образованию, специальность: учитель математики. Проработала всю жизнь преподавателем математики в педвузе.
Необходимо оговориться. Речь в дальнейшем пойдет о сумме, разности, произведении, частном чисел.
Ответы на данные вопросы хотя и простые, но вызывают затруднения у учащихся. Чтобы можно было более подробно рассмотреть эту обобщающую тему, предлагаю вашему вниманию полезный материал по ней. Заметка называется «Математика для блондинок».
Мне понравилась методика изучения.
Задается провокационный вопрос:
Пытаются заинтересовать (ни одна предложенная версия не является верной!)))
О других значениях данных слов не задумываюсь, математика затмевает все.)))
Это такие математические понятия.
Эти все понятия проходят в начальной школе.
В математике есть четыре простые операции, которые можно применить к двум числам и получить такие результаты:
I. Математические понятия СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ взаимосвязаны с математическими терминами СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ.
Все определения даются здесь на множестве натуральных чисел.
Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.
Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.
СУММА есть результат сложения чисел-слагаемых.
Каждой паре чисел можно поставить в соответствие число, которое состоит из стольких единиц, сколько их содержится в первом числе из пары, взятых столько раз, сколько единиц содержится во втором числе из пары. Это соответствующее таким образом паре чисел (они называются сомножителями) число называется ПРОИЗВЕДЕНИЕМ.
Деление есть операция, обратная умножению.
II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.
Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.
СУММА в переносном значении означает совокупность, общее количество чего-либо.
Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.
РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.
ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.
Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
Частное чисел – это итог процесса деления одного значения на второе. Пример:
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
Свойства умножения и деления
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства умножения
Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.
Узнаем, какие бывают свойства умножения и как их применять.
Переместительное свойство умножения
От перестановки мест множителей произведение не меняется.
То есть, для любых чисел a и b верно равенство: a * b = b * a.
Это свойство можно применять к произведениям, в которых больше двух множителей.
Сочетательное свойство умножения
Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.
То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).
Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.
Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.
То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.
Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.
В обратную сторону распределительное свойство умножения относительно сложения звучит так:
Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.
В обратную сторону распределительное свойство умножения относительно вычитания звучит так:
Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.
Свойство единицы при умножении
Если умножить любое целое число на единицу, то в результате получится это же число.
То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.
Свойства деления
Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.
Основные свойства деления целых чисел
И еще одно важное свойство деления, которое проходят в 5 классе:
Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.
Применим свойства деления на практике.
Пример 1
Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?
Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.
Пример 2
Вычислить: 500 * (100 : 5).
Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.
Ответ: 500 * (100 : 5) = 10000.
Пример 3
Упростить выражение: 27a – 16a.
Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Умножение натуральных чисел
Я сперва покажу на примере, для чего нужно умножение, а после дам определение умножения и подробно расскажу об этом действии.
Допустим, мы хотим купить 14 тетрадей по 22 рубля каждая. Планируя покупку, нам нужно знать, сколько мы заплатим за всю покупку?
Чтобы ответить на этот вопрос, нам нужно сложить стоимость каждой тетради, которую мы хотим купить. А, так мы запланировали покупку 14 тетрадей, тогда мы складываем 22 рубля 14 раз, то есть, находим сумму 14 слагаемых, каждое из которых равно 22 :
22+22+22+22+22+22+22+22+22+22+22+22+22+22=308 (то есть, 308 рублей).
Если размер и количество одинаковых слагаемых небольшие, мы без особого труда можем найти их сумму. Но что же делать, если слагаемые многозначные и их количество велико?
Умножение – это арифметическое действие сложения определенного количества одинаковых слагаемых.
Действие умножение – это частный случай действия сложение.
Число, которое является повторяющимся слагаемым, называется множимое (то, что множится, умножается).
Число, которое указывает на количество одинаковых слагаемых, называется множитель.
Множимое и множитель имеют общее название – сомножители.
Результат действия умножения называется произведением.
22 ∙14=308,
22x14=308,
22*14=308.
При записи от руки действие умножение принято обозначать при помощи точки, косой крест используется в основном при печати, а звездочка – в компьютерном наборе. Но даже и во время компьютерного набора грамотнее использовать точку или косой крест (букву х).
Прочитать действие умножения и результат можно такими способами:
Компоненты действия умножение для двух сомножителей:
Компоненты умножения для трех сомножителей и более:
Основные свойства умножения
Поскольку действие умножение является частным случаем действия сложение, то основные свойства сложения распространяются и на умножение.
Законы умножения и их следствия
Умножение обладает такими основными свойствами, называемые законами умножения, из которых вытекают остальные свойства и следствия:
Переместительный закон умножения.
Произведение двух или нескольких сомножителей от изменения их порядка не меняется.
Это значит, что значение произведения не зависит от порядка перемножения сомножителей, то есть, от порядка выполнения действия умножение.
Для двух сомножителей мы можем записать переместительный закон умножения в общем виде так:
ab=ba.
Допустим, нам нужно подсчитать количество отделений в шкафу (рис. 1).
Это свойство также верно для трех и более сомножителей.
К примеру, нам нужно подсчитать количество отделений в двух одинаковых шкафах (рис. 2).
5 ∙3+5 ∙3 =5 ∙3 ∙2.
15+15=15 ∙2,
30=30.
3 ∙5+3 ∙5=3 ∙5 ∙2,
15+15=15 ∙2,
30=30.
Значит, 5 ∙3 ∙2=3 ∙5 ∙2=30.
Поэтому, для трех сомножителей переместительный закон умножения в общем виде выглядит так:
abc=acb=bac=bca=cab=cba.
Сочетательный закон умножения.
Результат умножения трех и более чисел не изменяется, если любые из этих сомножителей заменить их произведением.
Следовательно, мы можем группировать множители между собой каким угодно образом, и выполнять действие умножения с этими группами.
В общем виде для трех сомножителей сочетательный закон умножения можно выразить так:
abc=a(bc)=(ab)c=b(ac).
Этот закон можно назвать следствием переместительного закона умножения.
Так, при подсчете количества отделений в двух шкафах на рисунке 2, мы можем сперва найти число отделений в одном шкафу, а потом умножить результат на 2 :
(5 ∙3) ∙2=15 ∙2=30,
(3 ∙5) ∙2=15 ∙2=30,
а можем сперва найти общее количество рядов отделений в обоих шкафах, а после умножить их на количество отделений в ряду:
(3 ∙2) ∙5=6 ∙5=30.
Как видите, результат во всех случаях одинаковый.
Особые случаи умножения: умножение единицы и нуля
Если в произведении двух чисел один из сомножителей единица, то произведение равно второму сомножителю:
a ∙1=1 ∙a=a.
А при умножении единицы на любое число (например, 1 ∙ 7 ) мы находим сумму семи единиц, то есть, то количество единиц, из которых состоит данное число. Следовательно, сумма этих единиц равна самому данному числу :
1+1+1+1+1+1+1=7.
Если в произведении любого количества сомножителей одним из сомножителей является нуль, то и произведение равно нулю:
a∙b∙0=0∙a∙b=a∙0∙c=0.
Умножение однозначных чисел
Умножение двух однозначных натуральных чисел a и b – это нахождения суммы b слагаемых, каждое из которых равно числу a, и при этом a и b являются натуральными числами.
Для облегчения вычисления, были посчитаны результаты умножения всех однозначных чисел друг на друга, и сведены в специальные таблицы умножения.
Умножение многозначного числа на однозначное
900+80+5+900+80+5+900+80+5+900+80+5.
Воспользуемся законами сложения и сгруппируем одинаковые слагаемые этого выражения вместе:
900+900+900+900+80+80+80+80+5+5+5+5,
(900+900+900+900)+(80+80+80+80)+(5+5+5+5).
Суммы в скобках мы можем заменить на произведение одинаковых слагаемых и числа этих слагаемых в каждых скобках:
900 ∙4+80 ∙4+5 ∙4.
Таким образом, чтобы умножить многозначное число на однозначное, достаточно умножить это однозначное число на количество единиц в каждом разряде многозначного числа, и сложить полученные результаты.
Умножение в столбик многозначного числа на однозначное
4 раза по 8 десятков – это 32 десятка. Прибавим к ним 2 десятка, которые получились после умножения однозначного числа на единицы, получим 32 десятка, то есть, 3 сотни и 2 десятка. Цифру 2 пишем под чертой в разряде десятков, а над разрядом сотен множимого 975 (в уме) ставим маленькую цифру 3 :
4 раза по 9 сотен – это 36 сотен. Прибавим к ним 3 сотни, которые держим в уме, получаем 39 сотен, или 3 тысячи и 9 сотен. Значит, пишем под горизонтальной чертой в разряде сотен цифру 9 и, поскольку в множимом 985 нет ни одной тысячи, то сразу запишем в результате под чертой цифру 3 в разряде тысяч:
Умножение многозначных чисел
Прежде чем рассказать, как в общем случае умножить одно многозначное число на другое, я расскажу о двух частных случаях умножения многозначных чисел:
Умножение на число, состоящее из единицы и любого количества нулей
327 ∙10 =3270
327 ∙100 =32700
Итак, чтобы умножить какое-нибудь число на другое, которое начинается на единицу, и заканчивается любым количеством нулей, достаточно к концу первого числа дописать столько нулей, сколько содержится во втором числе.
Умножение на число, которое начинается цифрами, и заканчивается любым количеством нулей
327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327+327.
(327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327)+ (327+327)+(327+327).
(327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2)+ (327 ∙2).
(327 ∙2) ∙10.
764 ∙3 =2292.
2292 ∙100 =229200.
Итак, чтобы умножить какое-нибудь число на другое, начинающееся любыми цифрами и заканчивающееся нулями, достаточно умножить первое число на число, образованное первыми цифрами второго, а к результату приписать справа столько нулей, сколько их было в конце второго числа.
Иными словами: нужно от второго числа отбросить нули в конце, умножить получившиеся числа, а к результату приписать справа столько нулей, сколько изначально отбросили.
Общее правило умножения чисел
Количество слагаемых ( 168 ) мы можем разложить на разрядные слагаемые ( 100+60+8 ) и согласно сочетательному закону сложения сгруппировать их следующим образом : сто слагаемых плюс шестьдесят слагаемых плюс восемь слагаемых.
Исходя из определения умножения, выражения в скобках мы можем представить не в виде суммы большого количества слагаемых, а как сумму произведений:
Таким образом, чтобы умножить два многозначных числа, достаточно последовательно умножить одно из этих чисел на количество единиц каждого из разрядов второго числа, и сложить полученные результаты.
Частное произведение – это число, полученное после умножения одного из сомножителей на количество единиц какого-либо разряда другого сомножителя.
Умножение в столбик многозначных чисел
При записи действия умножения в столбик сомножители располагаются друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел ; под множителем проводим горизонтальную черту, и ставим между сомножителями знак действия умножения:
В частных произведениях обычно не пишут (опускают) нули в конце числа для упрощения записи. При этом следует не забывать, что, первую полученную цифру частного произведения нужно писать в том разряде, цифру которого мы умножаем на множимое.
Некоторые особенности записи умножения в столбик
При записи нахождения произведения двух чисел в столбик существуют некоторые особенности, которые помогают сократить запись и упростить наглядность вычисления. Все они являются следствием свойств умножения.
Попробуйте самостоятельно доказать справедливость этого утверждения. Пишите в комментариях, получилось ли это у вас или нет.
Изменение произведения чисел при изменении его сомножителей
Если увеличить один из сомножителей в несколько раз, произведение также увеличится в это же число раз.
18 ∙2 =36
18 ∙6 =108.
По-другому и быть не может, и вот почему.
Первое произведение представляет собой сумму двух слагаемых :
18+18.
Второе произведение – это сумма шести таких же слагаемых :
18+18+18+18+18+18.
(18+18)+(18+18)+(18+18).
Если уменьшить один из сомножителей в несколько раз, произведение также уменьшится в это же число раз.
Попробуйте самостоятельно доказать правильность этого свойства. Пишите в комментариях, получилось ли это у вас?
Если увеличить один из сомножителей в несколько раз, а второй в это же число раз уменьшить, то произведение при этом не поменяется.
32 ∙8 =256,
Увеличим первый сомножитель в 4 раза, а второй во столько же раз уменьшим:
128 ∙2 =256.
Теперь уменьшим первый сомножитель произведения 32 ∙8 в 4 раза, а второй уменьшим в это же число раз:
8 ∙32 =256.
Умножение произведения на число и числа на произведение
Если необходимо умножить произведение на число, нужно любой сомножитель этого произведения умножить на данное число, а результат умножить последовательно на оставшиеся сомножители.
(a ∙b ∙c) ∙d =(a ∙d) ∙b ∙c =(b ∙d) ∙a ∙c =(c ∙d) ∙a ∙b
10 ∙7 =70 (просто приписываем к семерке нуль),
70 ∙9 =630 (находим по таблице умножения 7 ∙9 =63 и приписываем в конце нуль).
Когда я пишу «находим по таблице умножения», это означает, что мы вспоминаем эту строку из таблицы, а не ищем её там на самом деле. Таблицу умножения нужно знать наизусть!
Если необходимо умножить число на произведение, нужно умножить данное число на любой сомножитель, а результат умножить на оставшиеся сомножители.
a ∙(b ∙c ∙d) =(a ∙b) ∙c ∙d =(a ∙c) ∙b ∙d =(a ∙d) ∙b ∙c.
30 ∙3 =90,
90 ∙2 =180.
Распределительный закон умножения (умножение суммы на число)
Когда мы рассматривали умножение многозначного и однозначного чисел, мы раскладывали число 975 на его разрядные слагаемые ( 900+70+5 ), а потом умножали на 4 отдельно каждое это слагаемое. Аналогично можно поступать при умножении числа на любую сумму.
(5+2+4+9)+(5+2+4+9)+ (5+2+4+9).
Все эти слагаемые представляют собой одну сумму чисел, сгруппированных в определенные группы. Запишем их без скобок:
5+2+4+9+5+2+4+9+5+2+4+9,
а затем, используя переместительный и сочетательный законы сложения, сгруппируем одинаковые слагаемые:
Основываясь на определении действия умножение, так как мы имеем в каждых скобках одинаковые слагаемые, переписываем это выражение следующим образом:
5 ∙3+2 ∙3+4 ∙3+9 ∙3.
Распределительный закон умножения: для умножения суммы на любое число, необходимо каждое слагаемое этой суммы умножить на данное число, а затем сложить полученные произведения.
Согласно переместительному закону умножения, это свойство справедливо и при умножении числа на сумму.
Для умножения числа на сумму, необходимо умножить данное число на каждое слагаемое этой суммы, а результаты полученных произведения сложить.
(a+b+c+d)∙z =z∙(a+b+c+d) =a ∙z+b ∙z+c ∙z+d ∙z.
Название распределительный происходит от того, что действие умножения на сумму распределяется между каждым из слагаемых этой суммы.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 3