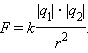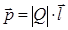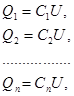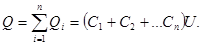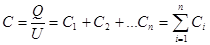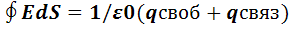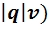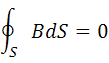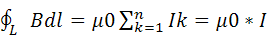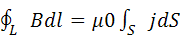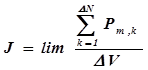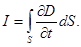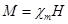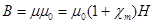что значит электрический заряд квантуется дискретен

Что значит электрический заряд квантуется дискретен

Основными объектами изучения в электродинамике являются электрические и магнитные поля, создаваемые электрическими зарядами и токами.

Электрическое поле

1.1. Электрический заряд. Закон Кулона

Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием.

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

Существует два рода электрических зарядов, условно названных положительными и отрицательными.

Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.

Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:

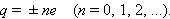В обычных лабораторных опытах для обнаружения и измерения электрических зарядов используется электрометр – прибор, состоящий из металлического стержня и стрелки, которая может вращаться вокруг горизонтальной оси (рис. 1.1.1). Стержень со стрелкой изолирован от металлического корпуса. При соприкосновении заряженного тела со стержнем электрометра, электрические заряды одного знака распределяются по стержню и стрелке. Силы электрического отталкивания вызывают поворот стрелки на некоторый угол, по которому можно судить о заряде, переданном стержню электрометра.

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.

На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.

Коэффициент пропорциональности в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).

В системе СИ элементарный заряд равен:

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции.

Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Рис. 1.1.4 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.

Принцип суперпозиции утверждает, что при заданном (фиксированном) распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.

Источник

Об электрическом заряде и его свойствах

В данной статье на основе представления о физической материи обосновывается понятие квантованности и ошибочность понятия дискретности электрического заряда.

Введение. Электрический заряд — одно из основных понятий учения об электричестве. Вся совокупность электрических явлений есть проявление существования, движения и взаимодействия электрических зарядов[1].

В 1729 году Ш. Дюфе установил, что существует два рода зарядов. Один образуется при трении стекла о шёлк, а другой — смолы о шерсть. Поэтому Дюфе назвал заряды «стеклянным» и «смоляным». Б. Франклин ввел понятие положительного и отрицательного зарядов: положительный заряд — это заряд тела, которое накапливает электричество, отрицательный — это заряд тела, теряющего электричество [2].

В 1870-80 г.г. ряд ученых (В. Вебер, Дж. К. Максвелл, Дж. Стони (Стоней), Г. Гельмгольц ) на основе анализа явления электролиза пришли к выводу о квантовании электрического заряда[3,4].

В 1891 году Дж. Стони, который поддерживал идею, что законы электролиза

Фарадея означают существование естественной единицы заряда, ввел термин – «электрон» следующим образом [5] : «При электролизе каждой химической связи, которая разрывается, присуще определенное количество электричества, одинаковое во всех случаях… Заряд такой величины связан в химическом атоме с каждой связью… Эти заряды, которые будет удобно называть «электронами», не могут быть отделены от атома; они не проявляют себя, если атомы находятся в химическом соединении».

В современной физике все понятия атомарного электричества конца ХIХ века были обобщены с понятиями атомарности материи (вещества) и концентрированно выражены в понятии электрон. Электрон это структурная единица атома вещества, носитель элементарного электрического заряда, а заряд электрона неделим и равен −1,6021766208(98)·10 −19 Кл (или −4,80320427(13)·10 −10 ед. заряда СГСЭ в системе СГСЭ) [3].

В начале XX века американский физик Р. Милликен опытным путём показал, что электрический заряд дискретен, то есть заряд любого тела составляет целое кратное от элементарного электрического заряда.

Таким образом были введены в научный обиход понятия элементарный электрический заряд, квантованность и дискретность электрического заряда, взаимосвязанные друг с другом, однако, и в настоящее время носящие характер предположения.

Свойства электрического заряда. Учитывая важнейший методологический фактор элементарного электрического заряда в теоретической физике (элементарный электрический заряд [4] — фундаментальная физическая постоянная, минимальная порция (квант) электрического заряда), все понятия, связанные с его представлением, должны были бы быть определены на соответствующей экспериментальной базе. Однако, тот факт, что электрический заряд в природе квантуется, т. е. переносится определенными порциями (квантами) и имеет дискретный характер, т. е. электрический заряд встречается в природе лишь в виде целого числа элементарных зарядов, пока еще носит характер предположения, поскольку удовлетворительного объяснения не найдено и в настоящее время [4]. Это обусловлено также тем, что решение проблемы квантования и дискретности электрического заряда традиционная физика ищет в мифологии. Основу таких мифов составляют представления о гипотетической элементарной частице – магнитный монополь [7], кварковая модель строения элементарных частиц [8], бинарная динамика структурогенеза и фрактальность внутренней структуры элементарных частиц [9], и др. [3, 4].

Исходя из вышеизложенного очевидно, что проблему квантования электрических зарядов необходимо искать в физической сущности электрического заряда и механизмов, в частности, процесса электролиза, где эта проблема проявляется.

В работе [10], в которой понятия квантования и дискретности обобщены, проведен “анализ обоснованности использования зарядовых чисел ионов и чисел электронов в уравнениях и формулах химии”, который “показывает, что дискретность электрических зарядов не следует из электрохимических экспериментов и законов электролиза и можно обойтись без привлечения в химию элементарных электрических зарядов”. Вывод из данной работы хорошо согласуется с представлениями Дж. Стони об электроне, в которых энергия, обусловленная электрическим зарядом, идет только на разрыв химической связи. Это означает, что движение носителей электрического заряда (электрический ток) заканчивается разрывом химической связи и все остальные процессы электролиза носят чисто химический характер. Носителем электрического заряда являются только элементарные частицы: “электрический заряд — … внутренняя характеристика элементарной частицы, определяющая ее электромагнитные взаимодействия” [1]. Каждая элементарная частица характеризуется определенным набором параметров, имеющих определенное значение. Электрический заряд, как характеристика элементарной частицы, также имеет определенное значение, которое можно назвать порцией или квантом электричества. Иначе, элементарная частица это носитель кванта электричества. Таким образом, квантование электрического заряда это следствие прежде всего структурно-уровневой организации физической материи [11], согласно которой элементарные частицы составляют один из структурных уровней организации физической материи и представляют собой “материальные объекты, которые нельзя разделить на составные части” [12].

Что касается понятия дискретности электрического заряда, то его обоснование следует рассмотреть в историческом аспекте процесса измерения величины элементарного электрического заряда.

Процесс измерения и обоснования результатов опытов проходил во время становления теории квантов, глубоко проникших во все области современной физики (имеется ввиду начало ХХ века) и переживавшей тяжелый кризис в начале ХХ века [18]. Результат Милликена хорошо согласовывался с результатом, полученным в рамках развивающейся квантовой концепции физики начала ХХ века (см. результат М. Планка) и укреплял ее обоснованность. А результаты Эренгафта и Иоффе не только не вписывались в эту концепцию, но и не могли быть объяснены ею. Поэтому они были подвергнуты критике и обструкции, несмотря на то, что авторитет Эренгафта, как ученого, был на порядок выше, чем у Милликена.

Тем не менее именно результаты Эренгафта и Иоффе решают проблему дискретности электрического заряда. Дело здесь в том, что работа Милликена априори строилась на никем не доказанном предположении, что опыты производятся над электроном (в современном понимании), имеющим постоянное значение электрического заряда, которое надо только возможно точнее измерить. Тогда, как Эренгафт полагал, что в природе существуют субэлектроны, несущие на порядок меньший заряд, или даже, что величина заряда может принимать непрерывно меняющиеся значения [17]. Дискуссионный вопрос о существовании субэлектронов физика начала ХХ века решить не могла вследствие своей неготовности (термин фотон был предложен в 1926 г.), а во вторых, внедрением в обиход феноменологической теории фотоэффекта, предложенной А. Эйнштейном (Нобелевская премия 1922), в целом оказавшейся не способной объяснить сущность фотоэффекта. Суть теории Эйнштейна сводится к описанию процесса выбивания фотоном от внешнего источника излучения электрона вещества. Выбивание электрона, структурного элемента атома вещества, это ничто иное как процесс разрушения атома вещества. Ни процесс разрушения атома вещества, ни то, что останется после того, как все электроны будут выбиты, теория Эйнштейна не рассматривает за ненадобностью.

В современном представлении процесс измерения электрического заряда Милликеном трактуется как внутренний фотоэффект [19]. Суть которого заключается в следующем. Источник внешнего облучения (ультрафиолетовая лампа, источник рентгеновского или радийного излучений) направляет поток, например, рентгеновского излучения (фотонов), на масляные капли (или пылинки металла), под действием которого внутри масляной капли изменяется концентрация носителей зарядов (внутренний фотоэффект). Одним из доказательств того, что внутри капли концентрируются фотоны, является процесс аннигиляции позитрона и электрона [20], подобный внутреннему фотоэффекту. В процессе аннигиляции протон-электронная пара атома вещества подвергается воздействию высоко энергетичных гамма-фотонов, в результате чего протон трансформируется в позитрон. Позитрон – электронная пара неустойчива. Взаимодействие позитрона и электрона ведет их к взаимоуничтожению (аннигиляции), при этом позитрон – электронная пара в процессе взаимодействия успевает сгенерировать два фотона. Процесс внутреннего фотоэффекта отличается тем, что атомы вещества подвергаются воздействию низко энергетичных фотонов, не приводящих к разрушению протон-электронных пар атомов вещества, но при этом протон-электронная пара атома вещества под воздействием внешнего излучения также генерирует два фотона.

Таким образом, на основании выше изложенного, если предположить, что субэлектроны Эренгафта и электроны Милликена это фотоны, то под воздействием внешнего источника излучения в опытах по измерению электрического заряда в масляных каплях и пылинках металла будут генерироваться фотоны, носители электрического заряда. Ввиду зависимости параметров фотона от его длины волны, основной формой представления фотона в различных процессах является спектр. В соответствии с представлениями современной физики фотоны характеризуются непрерывным энергетическим спектром. Не сложно показать, что электрический заряд, как неотъемлемая характеристика фотона, будет представлять собой тоже непрерывный спектр. Каждое вещество, в том числе и в опытах по измерению электрического заряда, характеризуется соответствующим энергетическим спектром, а значит и величина электрического заряда в опытах будет определятся соответствующим спектром генерируемых фотонов. Спектр фотонов является зависимой характеристикой от внешних факторов (температура, воздействие магнитные и электрических полей, параметры источника излучения и т. п.). Достичь приемлемой стабильности и учета всех внешних и внутренних факторов в опытах по измерению электрического заряда в начале ХХ века задача была не реальной. Этим и объясняется разброс данных в опытах Милликена, Эренгафта и Иоффе, особенно у Эренгафта.

Из выше изложенного следует, что электрический заряд фотона, как и его другие параметры, является нелинейной функцией длины волны фотона и имеет непрерывный спектр. При этом минимальные значения электрического заряда будут принадлежать фотонам инфракрасного диапазона. Данное обстоятельство позволяет говорить об элементарном электрическом заряде как о электрическом заряде фотона инфракрасного диапазона излучения (конкретное значение еще предстоит выяснить), но о его кратности говорить не приходится. Таким образом, дискретность электрического заряда, определенная Милликеном, понятие ошибочное и в природе не существует.

Выводы. Понятия квантования и дискретности электрического заряда появились вследствие непонимания сущности происходящих физических процессов, несовершенства и неполноты опытов по измерению величины электрического заряда.

Современное значение элементарного электрического заряда это частный случай, точнее линейное приближение более сложной зависимости электрического заряда от фундаментальных свойств материи – вещества, например, у фотона от длины волны.

Современная физика ищет решение проблемы квантованности электрического заряда в мифологии. Квантованность электрического заряда это следствие структурно-уровневой организации материи. Понятие дискретности электрического заряда ошибочно и в природе не наблюдается.

Процесс измерения величины электрического заряда потребовал усилий нескольких поколений известных ученых и завершился к началу ХХ века опытами Милликена, Эренгафта и Иоффе. При этом теоретическая физика ХХ века так и не смогла ответить на вопрос: что является материальным носителем этого электрического заряда. Обобщение понятий атомарности электричества и атомарности вещества привело к грубейшей ошибке, когда бездоказательно носителем элементарного электрического заряда был назначен электрон.

Источник

Вопрос№1. Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.

Вопрос№1. Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.

Вопрос№3.Электрический диполь и его поле.

Вектор 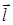, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя.

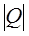
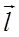
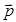
Вектор, совпадающий по направлению с плечом диполя и равный произведению заряда на плечо , называется электрическим моментом диполя или дипольным моментом.

Согласно принципу суперпозиции, напряженность поля диполя в произвольной точке

где и — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами.

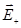
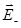
Поле равномерно заряженной бесконечной плоскости.

Поле объемно заряженного шара.

Напряженность поля вне равномерно заряженного шара описывается формулой : ( ),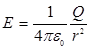

а внутри его изменяется линейно с расстоянием согласно выражению ( ).

Соединение конденсаторов.

У параллельно соединен­ных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна .

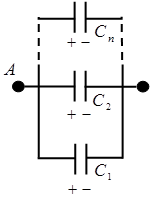
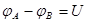
если емкости отдельных конденсаторов , то их заряды равны

а заряд батареи конденсаторов

Полная емкость батареи:

т. е. при параллельном соединении кон­денсаторов она равна сумме емкостей от­дельных конденсаторов.

У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи:

,

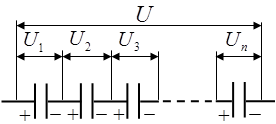
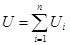
где для любого из рассматриваемых кон­денсаторов:

,

, откуда ,

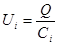
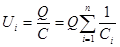
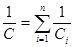
т. е. при последовательном соединении конденсаторов суммируются величины, об­ратные емкостям.

Теорема.

Теорема гаусса для электростатического поля в вакууме может быть распространена на электростатическое поле в среде, если под q понимать сумму всех свободных и связанных зарядов, охватываемых замкнутой гауссовой поверхностью S:

Напряженность электростатического поля, согласно Е=Е₀/(1+ )=Е₀/e, зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна e. Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачко­образное изменение. Поле характеризуется еще вектором электрического смещения, который для электрически изотроп­ной среды, по определению, равен

D=e₀eE.

Используя формулы e =1+ и Р= e₀Е, вектор электрического смещения можно выразить как

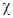
D=e₀E+P.

— диэлектрическая восприимчивость вещества,

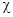
Сторонние силы. Э.Д.С.,

Против сил электрического поля могут действовать только силы неэлектрического происхождения, поэтому такие силы называются сторонними.

Сторонние силы — это силы неэлектрического происхождения, которые в отличие от кулоновских сил вызывают не соединение, а разделение разноименных электрических зарядов и поддерживают разность потенциалов проводников.

Электродвижущая сила – численно равна работе, совершаемой сторонними силами при перемещении по участку цепи единичного положительного заряда. –электродвижущая сила, действующая на участок цепи.

а) цепь замкнута:

б) Э.Д.С. на участке отсутствует:

Участок на котором отсутствует Э.Д.С. называется однородным, а участок содержащий Э.Д.С. называется неоднородным.

Закон Ома для участка цепи

Для участка цепи содержащей ЭДС будет иметь вид

Вопрос№15. Правила Киргофа и расчет электрических цепей.

Электрическая цепь- это система соединенных между собой токопроводящих элементов цепи. Если цепь состоит только из линейных эле­ментов, то она линейна, если же цепь содержит хотя бы один нелиней­ный элемент, то она становится нелинейной. Электрическая цепь изображается графически в виде своей эквива­лентной электрической схемы, на которой показано условное изобра­жение её элементов и соединение их друг с другом.

Физической основой расчёта электрической цепи, как линейной так и нелинейной являются законы Кирхгофа, первый из которых относит­ся к узлам цепи, а второй — к простым контурам.

Первый закон Кирхгофа (для узлов): алгебраическая сумма притека­ющих и вытекающих токов для любого узла цепи равна нулю:

(1)

В уравнении (1) притекающие и вытекающие токи берутся с противо­положными знаками.

Второй закон Кирхгофа (для контуров): алгебраическая сумма паде­ний напряжений на элементах цепи вдоль любого замкнутого конту­ра равна алгебраической сумме ЭДС, действующих в данном контуре

(2)

В уравнении (2) знаки величин U_k и E_k определяются по отношению к выбранному направлению обхода контура. Если ток I_k совпадает с на­правлением обхода, то падение напряжения на данном элементе U_k считается положительным, в противном случае оно отрицательно. Элек­тродвижущая сила E_k считается положительной, если её поле сторон­них сил совпадает с направлением обхода контура, в противном слу­чае она отрицательна. (Поле сторонних сил всегда направлено внутри источника от отрицательного к положительному полюсу).

Если элемент цепи не генерирует ЭДС, то падение напряжения на нём совпадает с разностью потенциалов на элементе. Для линейного эле­мента оно определяется 1 из закона Ома по заданному току и сопротив­лению . Для нелинейного элемента, не подчиняющегося зако­ну Ома, такое определение падения напряжения невозможно, в дан­ном случае оно определяется только из ВАХ нелинейного элемента по заданному току.

Источники магнитного поля

Магнитное поле создается (порождается) током заряженных частиц, или изменяющимся во времени электрическим полем, или собственными магнитными моментами частиц (последние для единообразия картины могут быть формальным образом сведены к электрическим токам).

Основной силовой характеристикой магнитного поля является вектор магнитной индукции 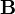(вектор индукции магнитного поля).

Вектор магнитной индукции В численно равен отношению силы, действующей на заряж. частицу со стороны магнитного поля, к произведению абсолютного значения заряда и скорости частицы, если направление скорости частицы таково, что эта сила максимальна. В=(F)max/(

Сила Лоренса.

На частицу движущуюся в магнитном поле, действует Сила Лоренса определяющаяся выражением:F=q[vхB]. Модуль магнитной силы равен: F=qvB sin a

Направление силы Лоренса «правило левой руки»:если ладонь левой руки расположить так, чтобы вектор магнитной индукции В входил в ладонь, а 4 пальца направить вдоль скорости + частицы, то отставленный на 90 градусов большой палец укажет направление силы Лоренса.Если имеются одновременно электрическое и магнитное поля, сила, действующая на заряженную частицу, равна F=qE+q[vхB]

Теорема Гаусса

Магнитный поток сквозь произвольную замкнутую поверхность равен нулю:

Пусть ток I течет по проводнику, намотанному по винтовой линии на поверхность цилиндра. Такой обтекаемый током цилиндр называют соленоидом. Пусть на единицу длины соленоида приходится n витков проводника. Если шаг винтовой линии достаточно мал, то каждый виток соленоида можно приближенно заменить замкнутым витком. Будем также предполагать, что сечение проводника настолько мало, что ток в соленоиде можно считать текущим по его поверхности.

Опыт и расчет показывают, что чем длиннее соленоид, тем меньше индукция магнитного поля снаружи его. Для бесконечно длинного соленоида магнитное поле снаружи отсутствует вообще. Из изображения симметрии ясно, что линии вектора В внутри соленоида направлены вдоль его оси, причем вектор В составляет с направлением тока в соленоиде правовинтную систему.

Уже то, что мы выяснили относительно конфигурации магнитного поля соленоида, подсказывает выбрать прямоугольный контур так как показано на Рис. 13. Циркуляция вектора В по данному контуру равна Bl, и контур охватывает ток nlI. Согласно теореме о циркуляции, откуда следует, что внутри длинного соленоида Т.е. поле внутри длинного соленоида однородно (за исключением областей, прилегающих к торцам соленоида, но этим при расчетах зачастую пренебрегают). Произведение nI называют числом ампервитков.

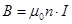
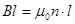
Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора B).

Циркуляция магнитной индукции поля в вакууме вдоль произвольного замкнутого контура L равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром(т.е. на электрический ток через поверхность S, натянутую на этот контур)

Закон полного тока можно записать в виде:

j-плотность тока в пределах малого элемента dS поверхности S, натянутой на контур L.

Намагниченность

Для характеристики степени намагничивания того или иного вещества используется понятие намагниченности J, которая равна магнитному моменту единицы объема магнетика:

Другими словами, намагниченность J – это количественная мера намагничивания вещества.

Магнитная проницаемость

Магнитная проницаемость является количественной характеристикой, определяющей изменение поля в веществе. Это безразмерная величина, которая, как правило, находится экспериментально:

Она показывает, во сколько раз магнитная индукция B в вытянутом (длинном) образце, помещенном в длинный соленоид (соленоид мы приводим в качестве примера) отличается от магнитной индукции 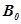в пустом соленоиде (т.е. в вакууме). Значения магнитной проницаемости сильно зависят от состава и строения вещества, т.е. от рода (типа) магнетика.

Все вещества при рассмотрении их магнитных свойств принято называть магненитками.Три основные группы магнетиков:

Диамагнетики; Парамагнетики; Ферромагнетики;

Диамагнетикаминазывают вещества, которые намагничиваются во внешнем магнитном поле в направлении, противоположном направлению вектора магнитной индукции поля. К диамагнетикам относятся вещества, магнитные моменты атомов, молекул или ионов которых в отсутствие внешнего магнитного поля равна нулю. Диамагнетиками являются инертные газы, молекулярные водород и азот, висмут, цинк, медь, нафталин и т.д.

Намагниченность диамагнетиков: J=n ,где – магнитный момент, n0-концентрация атомов.

Парамагнетикаминазываются вещества, которые намагничиваются во внешнем магнитном поле в направление вектора B. К парамагнетикам относятся многие металлы, некоторые переходные металлы, а также сплавы этих металлов., кислород, оксид азота, оксид марганца. В отсутствии внешнего магнитного поля парамагнетик не намагничен, так как из-за теплового движения собственные магнитные моменты атомов ориентированы совершенно беспорядочно(J=0).при внесении парамагнетического вещества в магнитное поле парамагнетик намагничивается «по полю», т.е. в направлении B.

Намагниченность парамагнетиков зависит от параметра a=PmB/(kT), где k-постоянная Больцмана, T-термодинамическая температура. J=n0PmL(a), где n0-концентрация атомов парамагнетика.

Ток смещения.

Для установления количественных соотношений между изменяющимся электрическим полем Максвелл вел в рассмотрение так называемый ток смещения.

Рассмотрим цепь переменного тока, содержащую конденсатор.

Между обкладками заряжающегося и разряжающего конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор “протекают” токи смещения, причем в тех участках, где отсутствуют проводники.

По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток проводимости, равный току в проводящих проводах. Тогда можно утверждать, что токи проводимости ( 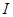) и смещения ( ) равны. Ток проводимости вблизи обкладок конденсатора для общего случая можно записать так:

Сравнивая это выражение с , имеем . (3)

Данное выражение было названо Максвеллом плотностью тока смещения. Направление вектора , а следовательно, и вектора совпадает с направлением вектора , как это следует из формулы (3).

Подчеркнем, что из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространстве магнитное поле. Следует отметить, что ток смещения по своей сути – это изменяющееся со временем электрическое поле. Ток смещения поэтому существует не только в вакууме или в диэлектриках, но и внутри проводников по которым течет переменный ток. Однако в данном случае он пренебрежительно мал по сравнению с током проводимости.

Максвелл обобщил закон полного тока, добавив в правую часть уравнения ток смещения сквозь поверхность, натянутую на замкнутый контур L:

Второе уравнения Максвелла: циркуляция вектора Н напряженности магнитного поля по произвольному неподвижному замкнутому контуру L, мысленно проведенному в электромагнитном поле, равна алгебраической сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур.

Материальные уравнения

В слабых электромагнитных полях, сравнительно медленно меняющихся в пространстве и во времени, в случае изотропных, неферромагнитных и несегнетоэлектрических сред справедливо приближение, в котором поляризуемость и намагниченность линейно зависят от приложенных полей.

СИ: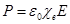

СИ: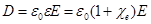

где 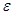— относительная диэлектрическая проницаемость, — относительная магнитная проницаемость. Размерные величины (в единицах СИ — Ф/м) и (в единицах СИ — Гн/м), возникающие в системе СИ, называются абсолютная диэлектрическая проницаемость и абсолютная магнитная проницаемость соответственно.

Вопрос№1. Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.

Источник