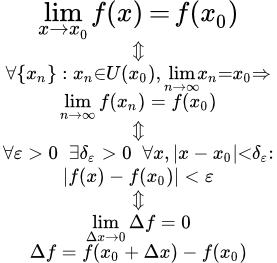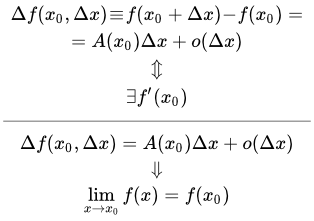что значит функция определена в точке
Определение непрерывности функции в точке
Непрерывность в точке
Определение непрерывности
Определение непрерывности функции в точке
Функция f ( x ) называется непрерывной в точке x 0 , если она определена на некоторой окрестности U ( x 0) этой точки, включая саму точку, и если предел при x стремящемся к x 0 существует и равен значению функции в x 0 :
.
Здесь подразумевается, что x 0 – это конечная точка. Значение функции в ней может быть только конечным числом.
Если привлечь сюда определение конечного предела функции в конечной точке, то можно дать развернутую формулировку определения непрерывности функции. Поскольку имеется два равносильных определения предела функции (по Коши и по Гейне), то можно дать, как минимум, еще два эквивалентных определения непрерывности.
Запишем эти определения с помощью логических символов существования и всеобщности.
По Гейне:
.
По Коши:
.
Определение отсутствия непрерывности
Непрерывность на концах отрезка
Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x 0 , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x 0 равен значению функции в x 0 :
.
Примеры
Пример 1
Используем определение по Гейне
Используем определение по Коши
Пример 2
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Непрерывность функции в точке, разрывы первого и второго рода
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
Решение
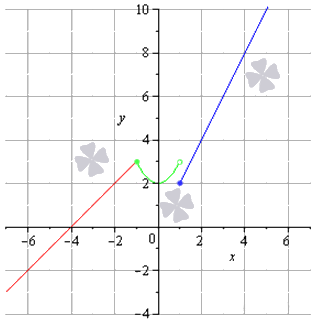
Соответствующая последовательность значений функций выглядит так:
на чертеже они обозначены зеленым цветом.
Соответствующая последовательность функций:
на рисунке обозначена синим цветом.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
Устранимый разрыв первого рода
Решение
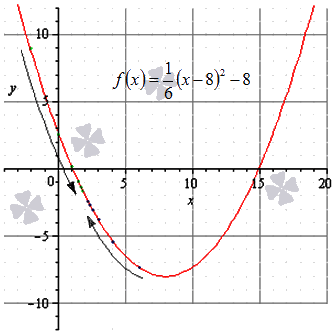
Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Решение
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
Ответ: в конечном счете мы получили:
Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Решение
Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:
Ей соответствует последовательность значений функции:
Построение графиков функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Дифференцируемые функции в точке – определение и свойства
Определение дифференцируемой функции
Как мы увидим ниже, определение дифференцируемой функции одной переменной эквивалентно существованию ее производной. Тогда возникает вопрос – почему нельзя сразу дать определение, что дифференцируемая функция – это функция, имеющая производную?
Ответ на этот вопрос раскрывается при рассмотрении функций нескольких переменных. Дело в том, что производные вычисляются только от функций, зависящих от одной переменной. Для функций двух и более переменных, вначале выбирают направление приближения к заданной точке (например, ось x или ось y ), а затем по этому направлению вычисляют производную. Поэтому в любой точке имеется бесконечное множество производных по различным направлением. Из-за этого производные не фигурируют в определении дифференцируемой функции.
Свойства дифференцируемой функции
Таким образом, в случае функции от одной переменной, дифференцируемость функции в точке эквивалентно существованию производной в этой точке. Забегая вперед укажем, что в случае функций многих переменных, для того чтобы функция была дифференцируемой в точке, необходимо, чтобы она имела в этой точке частные производные, и достаточно, чтобы она имела в этой точке непрерывные частные производные.
Доказательства теорем
Связь дифференцируемости функции с существованием производной
В нашем случае это означает, что
.
Отсюда
.
Связь дифференцируемости функции с ее непрерывностью
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Что значит функция определена в точке
Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `ain R`, за исключением, быть может, самой точки `a`.
Число `A` называется пределом функции `y=f(x)` в точке `a`, если для любой последовательности `(x_n)` из области её определения такой, что `x_n!=a` и `lim_(n->oo)x_n=a` выполняется равенство `lim_(n->oo)f(x_n)=A`.
Обозначение: `lim_(n->oo)f(x)=A`, или `f(x)->A` при `x->a`.
В определении предела рассматриваются значения `x_n`, не равные `a`, поэтому в самой точке `a` функция `y=f(x)` может быть не определена; если значение `f(a)` определено, то оно не обязано совпадать с `A`. К тому же, поскольку последовательность `(f(x_n))` имеет не более одного предела, получаем, что если функция `y=f(x)` имеет предел при `x->a`, то этот предел единственный.
На рис. 2 изображена лишь одна последовательность `(x_n)`, которая к тому же является монотонной. Важно понимать, что `lim_(n->oo)f(x_n)=A` для любой последовательности `(x_n)` с условием `x_n!=a` и `lim_(n->oo)x_n=a`.
Доказать, что `lim_(n->oo)x=a`.
Очевидно, функция `f(x)=x` определена на любом интервале, содержащем `a`. Выберем произвольную последовательность `(x_n)` такую, что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда `f(x_n)=x_n` и, значит, `lim_(n->oo)f(x_n)=a`.
Доказать, что при `a>0lim_(n->a)sqrtx=sqrta`.
Функция `f(x)=sqrtx` определена при `x>=0` и, следовательно, определена на некотором интервале, содержащем `a`. Выберем произвольную последовательность неотрицательных чисел `x_n!=a`, что `lim_(n->oo)x_n=a`. Нам нужно показать, что `lim_(n->oo)sqrtx_n=sqrta`. Фиксируем произвольное `epsilon>0`, тогда найдётся такое число `k`, что при `n>k` выполняется неравенство `|x_n-a| 1)(x^2-1)/(x-1)=2`.
Функция `f(x)=(x^2-1)/(x-1)` определена на любом интервале, содержащем `x=1`, кроме этой точки. Поскольку при `x!=1` имеет место равенство `f(x)=x+1`, то для любой последовательности `(x_n)` такой, что `x_n!=1` и `lim_(n->oo)x_n=1` выполняется `lim_(n->oo)f(x_n)=lim_(n->oo)x_n+1=2`.
Пусть функции `y=f(x)`, `y=g(x)` определены на некотором интервале, содержащем точку `a in R`, за исключением, быть может, самой точки `a`, `lim_(x->a)f(x)=A` и `lim_(x->a)g(x)=B`. Тогда
3) если дополнительно `g(x)!=0` при `x!=a`, `B!=0`, то `lim_(x->a)(f(x))/(g(x))=A/B`.
Эти свойства вытекают из арифметических операций над пределами последовательностей (теорема 2.2). Приведём доказательство для свойства 2. Остальные доказываются аналогично.
Пусть некоторая произвольная последовательность `(x_n)` из интервала, на котором определены функции, такова что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда по определению предела функции `lim_(n->oo)f(x_n)=A` и `lim_(n->oo)g(x_n)=B`. По пункту 2 теоремы 2.2 `lim_(n->oo)f(x_n)g(x_n)=AB`. По определению предела функции получаем, что `lim_(x->a)f(x)g(x)=AB`.
Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `a`. Функция `y=f(x)`называется непрерывной в точке `a`, если `lim_(x->a)f(x)=f(a)`, т. е. если для любой последовательности `(x_n)` из области определения функции такой, что `lim_(n->oo)x_n=a`, выполняется равенство `lim_(n->oo)f(x_n)=f(a)`.
Отметим два обстоятельства, связанных с определением непрерывности. Во-первых, оговорка `x_n!=a` здесь не нужна, т. к. при `x_n=a` значения `f(x_n)` равны `f(a)`. Во-вторых, важно понимать, что если функция `y=f(x)` непрерывна в точке `a`, то
1) она определена в точке `a`;
2) существует `lim_(x->a)f(x)=A` и
Если хотя бы один из пунктов 1) – 3) не выполнен, то функция не является непрерывной в точке `a`.
Многочлен является непрерывной на всей числовой прямой функцией.
Из теоремы 3.1 вытекает, что если функции `y=f(x)`, `y=g(x)` непрерывны в точке `a`, то функции `y=f(x)+-g(x)`, `y=f(x)g(x)`, `y=f(x)//g(x)` `(g(a)!=0)` также непрерывны в `a`.
Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
Функция `y=|x|` непрерывна на всей числовой прямой.
Вообще, все элементарные функции, изучаемые в школьном курсе, непрерывны в каждой точке, в окрестности которой эти функции определены.