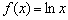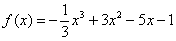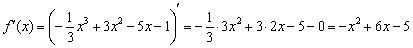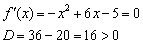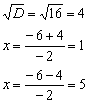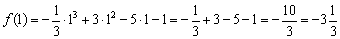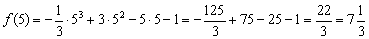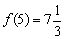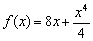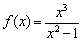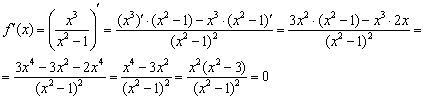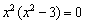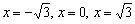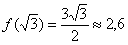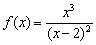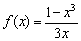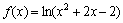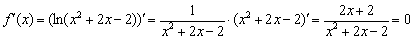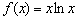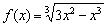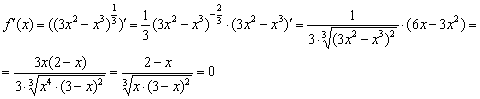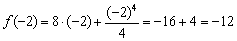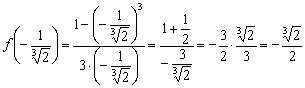что значит исследовать функцию на монотонность
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Исследование функций на монотонность
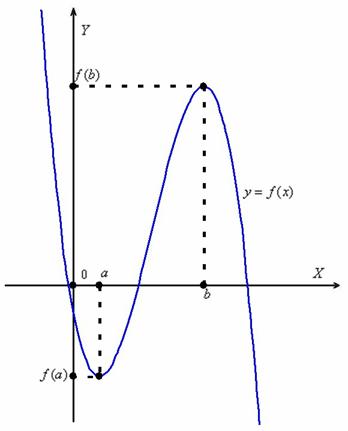
Говоря о смысле производной, мы замечали, что у возрастающих функций она принимает положительные значения, а у убывающих – отрицательные. Убедиться в этом можно с помощью графиков. Действительно, если провести касательную к возрастающей ф-кции, то она образует с осью Ох острый угол, а потому тангенс этого угла (а он как раз равен произ-ной) окажется положительным числом:
Если же ф-кция убывает, то касательная образует с осью Ох тупой угол, чей тангенс будет отрицательным:
Действительно, произ-ная у′ = 2х принимает отрицательные значения при х∈ (– ∞;0) и оказывается положительной при х∈(0; + ∞). Заметим, что в граничной точке произ-ная равна нулю.
Произ-ная положительна во всех точках, кроме х = 0. При х = 0 у′ также оказывается равной нулю. Однако мы можем сказать, что у′ неотрицательна на всей числовой прямой.
Можно привести пример ф-кции
Сама ф-кция убывает на всей числовой прямой, а её произ-ная неположительна на ней.
Рассмотрим особый случай, когда у ф-кции произ-ная одновременно и неположительна, и неотрицательна на отрезке. Как ни сложно догадаться, это означает, что производная равна нулю. Мы помним, что нулю равна произ-ная константы:
В качестве примера приведем ф-кцию у = 2. Её произ-ная на всей числовой прямой равна нулю:
При этом ф-кция и не убывает, и не возрастает на числовой прямой:
Рассматривая все эти примеры, можно сделать вывод, что для возрастания ф-кции на промежутке достаточно, чтобы её произ-ная принимала на этом отрезке только положительные отрезки:
Аналогично можно сформулировать и достаточный признак убывания ф-кции:
Сформулированные признаки не охватывают тех ситуаций, когда произ-ная в отдельных точках промежутка обращается в ноль. Если произ-ная равна нулю на всём промежутке, то ф-кция на нем остается неизменной (как в случае с функцией у = 2). Если же производная обращается в ноль только в отдельных точках (случай у = х 3 и у = х 2 ), то эти точки оказываются граничными для промежутков возрастания и промежутков убывания функции. В этих случаях эти граничные точки добавляют в соответствующие промежутки.
Задание. Докажите, что функция
возрастает при любом значении аргумента.
Решение. Найдем произ-ную у′:
Найдем, при каких значениях х произ-ная у′ оказывается положительной. Для этого запишем неравенство:
Множитель (5х 2 + 6) при любом х положителен, а потому мы можем поделить обе части неравенства на него и преобразовать его к виду
Его решениями являются промежутки (– ∞; 0) и (0; + ∞), а при х = 0 произ-ная оказывается равной нулю, то есть это граничная точка. Значит, промежутками возрастания функции являются (– ∞; 0] и [0; + ∞). Обратите внимание, что мы добавили в каждый из промежутков граничную точку х = 0. Но объединением этих промежутков является вся числовая прямая:
Получается, что ф-кция возрастает при любом х.
Теперь попытаемся найти промежутки возрастания и убывания функции
Для их нахождения определим, где произ-ная положительна, а где отрицательна. Для этого сначала найдем произ-ную:
Решим неравенство у′ > 0, при этом мы используем метод интервалов:
Отмечаем нули на координатной прямой и расставляем знаки промежутков:
Напомним, что для определения знаков промежутков можно просто выбрать на каждом из них одну точку и подставить её в неравенство. Например, на интервале х∈(– ∞; – 1) возьмем число – 2:
Итак, произ-ная положительна на промежутках (– ∞; – 1) и (0; + ∞). При х = 0 и х = 1 произ-ная обращается в ноль – это граничные точки, которые надо добавить в промежутки возрастания. То есть ф-кция возрастает на промежутках (– ∞; – 1] и [0; + ∞).
Более того, можно определить, является ли экстремум точкой минимума или точкой максимума. Если произ-ная меняет знак с плюса на минус, то это точка максимума, а если с минуса на плюс – то это точка минимума.
Для примера рассмотрим ф-кцию
Попытаемся найти ее экстремумы. Для этого вычислим производную:
Найдем нули произ-ной:
Теперь отметим на координатной прямой нули ф-кции. Они разобьют числовую прямую на три промежутка. Расставим знаки производной на этих промежутках:
Знаки на промежутках можно определить, просто подставив в произ-ную одно из чисел из промежутка:
Получается, что в точке х = 0 произ-ная меняет знак с «+» на (–), а в точке х = 2 знак произ-ной не меняется. Это значит, что точка х = 0 является точкой минимума, а х = 2 – это вообще не экстремум ф-кции:
В общем случае для определения экстремумов ф-кции можно руководствоваться следующей схемой:
До этого мы рассматривали случаи, когда ф-кция была определена при любом значении аргумента. Теперь изучим ф-кцию
Ее особенностью является то, что она не определена при х = 0, так как при таком значении аргумента получается деление на ноль. Вычислим у′:
Теперь найдем нули произ-ной:
Выражение х 2 + 4 при любом х не равно нулю, а потому на него можно поделить уравнение:
Теперь на числовой прямой мы должны отметить две найденные критические точки. Но также на ней следует отметить число х = 0, так как в этой точке ф-кция не определена:
Обратите внимание, что точка х = 0 НЕ является экстремумом, хотя кажется, что в ней ф-кция меняет свой знак. Дело в том, ф-кция не существует при таком значении аргумента. Это значит, что х = 0 – это асимптота графика. График ф-кции будет выглядеть примерно так:
Выпуклость и вогнутость функций
Нарисуем две немного отличающиеся друг от друга возрастающие ф-кции:
Видно, что эти графики будто выгнуты в разные стороны. Оказывается, в математике есть специальное свойство ф-кций, которое указывает на направление, в котором выгнуты их графики. Левая ф-кция является вогнутой функцией, а правая – выпуклой функцией.
Определить, выпукла или вогнута ф-кция, очень просто. Достаточно провести к графику касательную. Если она проходит выше графика, то это указывает на вогнутость функции, а если ниже, то она выпукла:
Ранее мы уже заметили, что точка х = 0 для ф-кции у = х 3 – этой пример критической точки, которая не является экстремумом. Действительно, произ-ная ф-кции у = х 3 имеет вид
и она обращается в ноль при х = 0, однако в этой точке ф-кция возрастает. Это подсказывает нам, что критические точки, в которых ф-кция НЕ меняет своего знака, являются точками перегиба. И это действительно так.
Заметим, однако, что в общем случае точка перегиба может и вовсе не являться критической точкой ф-кции. В рамках школьного курса мы не будем детально изучать выпуклость функций и точки перегиба. Отметим лишь, что для их поиска необходимо вычислять уже не только первую, но и вторую произ-ную функции.
Исследование функций и построение их графиков
Ранее мы строили графики ф-кций в основном «по точкам». То есть мы просто вычисляли значение ф-кции при различных значениях х, отмечали получившиеся точки на координатной плоскости, а потом соединяли их плавной кривой. Однако при этом можно упустить некоторые важные особенности ф-кций – наличие у них минимумов и максимумов, точки их пересечения с осями координат и т.п. Поэтому в математике используют особый алгоритм для построения графиков ф-кции, который называют «исследованием функции».
Последовательность алгоритма следующая:
Заметим, что у ф-кции можно также найти точки перегиба ф-кции, исследовать ее на выпуклость и вогнутость, однако в рамках программы 11 класса это не делается.
Сразу скажем, что исследование ф-кции – это трудоемкая задача. Она не очень сложная, но требует больших затрат времени и бумаги.
Для начала рассмотрим относительно простой пример ф-кции
Область ее определения – это вся числовая прямая. Ф-кция не является ни четной, ни нечетной. Доказать это на примере конкретной точки. Возьмем х = 1:
Однако у нас это условие явно не выполняется, ведь 0 ≠ 4. Если бы ф-кция была нечетной, то выполнялось бы условие
Оно также не выполняется, так как 0 ≠ – 4.
Вычислим произ-ную ф-кции:
Произ-ная также определена на всей числовой прямой. Для поиска критических точек приравняем ее к нулю:
Получили две критические точки. Отметим их на прямой и расставим знаки:
Итак, мы смогли найти точку максимума функции, равно как и ее точку минимума.
Сразу же вычислим значение ф-кции в ее экстремумах:
Для расстановки знаков возьмем по одному значению из каждого промежутка. Например, можно взять числа (– 2), 0 и 2:
Далее находим, где прямая пересекается с осью Оу, для чего подставляем в ф-кцию значение х = 0:
Получили точку (0; 2). Для нахождения точек пересечения графика с горизонтальной остью Ох надо приравнять всю ф-кцию к нулю:
Это кубическое уравнение. Решить его можно методом подбора корней и последующим делением многочлена на многочлен. Не останавливаясь на подробностях решения, укажем, что его корнями являются числа (– 2) и 1, а других корней. Убедиться в этом можно, просто подставив в уравнение эти числа.
Следующий шаг – определение промежутков знакопостоянства. Для этого надо решить неравенство у(х) > 0:
Это неравенство решается методом интервалов. Он сводится к тому, что находятся нули левой части, которые мы уже нашли – это числа (– 2) и 1. Далее они отмечаются на прямой, после чего на образовавшихся промежутках проставляются знаки:
Знаки определяем, выбирая по одной точке из каждого промежутка:
Достаточно очевидно, что при х→∞ сама ф-кция также стремится к бесконечности. Если же х→ – ∞, то и у→ – ∞.
Представим найденную нами информацию в виде таблицы. В верхней строке будем записывать промежутки и отдельные точки, а ниже – особенности ф-кции на этих промежутках (возрастает ф-кция или убывает, положительна она или отрицательна и т.п.):
В итоге график ф-кции будет иметь следующий вид:
Теперь исследуем более сложную ф-кцию
Начнем с области определения. Знаменатель дроби не может равняться нулю, а потому
Итак, аргумент ф-кции может принимать любые значение, кроме 1 и (– 1). Поэтому её область определения (она обычно обозначается как D (x)) можно записать так:
Далее проверяем ф-кцию на четность или нечетность. Напомним, что для этого надо подставить в нее вместо аргумента х аргумент (– х):
Мы получили у(х). Это означает, что ф-кция четная, а ее график симметричен относительно оси Оу.
Следующий шаг – находим произ-ную ф-кции:
Заметим, что область определения произ-ной полностью совпадает с областью определения самой ф-кции. Поэтому у ф-кции нет таких критических точек, в которых произ-ная не существует.
Теперь произ-ную можно приравнять к нулю:
Мы нашли всего одну критическую точку. Отметив ее на координатной прямой, можно выяснить, что она является точкой максимума. При этом стоит также отметить точки х = 1 и х = – 1, в которых ф-кция не определена (их ещё называют точками разрывов):
Для определения знаков произ-ной достаточно вычислить её значение в одной точке на каждом получившемся промежутке. Возьмем значения (– 2), (– 0,5), 0,5 и 2
Найдем точку пересечения графика с осью Оу, для чего подставим в ф-кцию значение х = 0:
Получили точку (0; – 1).
Далее находим точку пересечения графика с осью Ох. Для этого подставим в ф-кцию значение у = 0 и решим получившееся уравнение:
Числитель дроби в правой части при любом значении х положителен, то есть не равен нулю. Это значит, что уравнение не имеет решения. Отсюда вывод – график НЕ пересекается с осью Ох.
Следующий шаг – это определение промежутков знакопостоянства функции. Чтобы найти, при каких значениях аргумента ф-кция положительная, составим неравенство:
Это дробно-рациональное неравенство. Для его решения надо отметить на координатной прямой те значения х, при которых либо знаменатель, либо числитель обращается в ноль. Числитель при любом аргументе положителен, а нулями знаменателя являются точки х = – 1 и х = 1:
Знаки на промежутках определяем, подставляя точки из промежутков в ф-кцию:
Далее следует исследовать поведение ф-кции вблизи при х →∞ и х→ –∞. Для этого преобразуем ф-кцию, выделив целую часть:
При х→∞ число (х 2 – 1) также стремится к бесконечности, а дробь
будет стремиться к единице. Аналогично можно убедиться, что при х→ – ∞ ф-кция также стремится к единице.
Все полученные данные можно удобно представить в табличном виде:
На основании этих результатов строим график:
Из рисунка видно, что область значений ф-кции имеет вид
Итак, мы узнали, что с помощью производной можно определять промежутки, на которых функция возрастает и убывает, а также находить ее минимумы и максимумы. Эти навыки помогают при решении многих практических задач, когда требуется найти такое значение некоторых параметров, при которых какая-то величина принимает максимальное или минимальное значение. Например, продавцы товара могут назначать такую цену на свою продукцию, которая принесет им максимальный доход (просто назначить как можно большую цену нельзя, так как слишком дорогой товар никто не купит). Более подробно такие задачи мы рассмотрим подобные задачи в следующих уроках.
Возрастание, убывание и экстремумы функции
А сегодня в воздухе витает дух редкого единодушия, и я прямо чувствую, что все присутствующие горят желанием научиться исследовать функцию с помощью производной. Поэтому на экранах ваших мониторов незамедлительно появляется разумная добрая вечная терминология.
Зачем? Одна из причин самая что ни на есть практическая: чтобы было понятно, что от вас вообще требуется в той или иной задаче!
Монотонность функции. Точки экстремума и экстремумы функции
Рассмотрим некоторую функцию 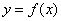
На всякий случай сразу избавимся от возможных иллюзий, особенно это касается тех читателей, кто недавно ознакомился с интервалами знакопостоянства функции. Сейчас нас НЕ ИНТЕРЕСУЕТ, как расположен график функции относительно оси 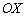
Функция возрастает на интервале, если для любых двух точек этого интервала, связанных отношением 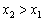
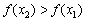
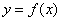
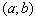
Аналогично, функция убывает на интервале, если для любых двух точек данного интервала, таких, что 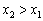
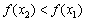
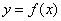
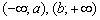
Если функция возрастает или убывает на интервале, то её называют строго монотонной на данном интервале. Что такое монотонность? Понимайте в буквальном смысле – однообразие.
Также можно определить неубывающую функцию (смягчённое условие 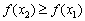
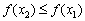
Теория рассматривает и другие подходы к определению возрастания/убывания функции, в том числе на полуинтервалах, отрезках, но чтобы не выливать на вашу голову масло-масло-масляное, договоримся оперировать открытыми интервалами с категоричными определениями – это чётче, и для решения многих практических задач вполне достаточно.
Таким образом, в моих статьях за формулировкой «монотонность функции» почти всегда будут скрываться интервалы строгой монотонности (строгого возрастания или строгого убывания функции).
Окрестность точки. Слова, после которых студенты разбегаются, кто куда может, и в ужасе прячутся по углам. …Хотя после поста Пределы по Коши уже, наверное, не прячутся, а лишь слегка вздрагивают =) Не беспокойтесь, сейчас не будет доказательств теорем математического анализа – окрестности мне потребовались, чтобы строже сформулировать определения точек экстремума. Вспоминаем:
Окрестностью точки называют интервал, который содержит данную точку, при этом для удобства интервал часто полагают симметричным. Например, точка 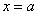
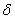

Собственно, определения:
Точка 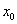
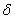
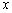
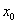
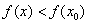
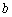
Точка 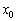
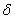
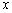
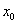
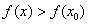
Примечание: требование симметричности окрестности вовсе не обязательно. Кроме того, важен сам факт существования окрестности (хоть малюсенькой, хоть микроскопической), удовлетворяющей указанным условиям
Точки 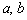
Как понимать слово «экстремум»? Да так же непосредственно, как и монотонность. Экстремальные точки американских горок.
Как и в случае с монотонностью, в теории имеют место и даже больше распространены нестрогие постулаты (под которые, естественно, подпадают рассмотренные строгие случаи!):
Точка 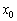
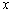
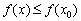
Точка 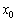
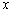
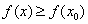
Заметьте, что согласно последним двум определениям, любая точка функции-константы (либо «ровного участка» какой-нибудь функции) считается как точкой максимума, так и точкой минимума! Функция 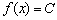
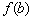
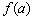
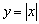
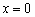
Да, кстати, о королевских особах:
– значение 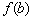
– значение 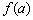
Общее название – экстремумы функции.
Пожалуйста, будьте аккуратны в словах!
Точки экстремума – это «иксовые» значения.
Экстремумы – «игрековые» значения.
! Примечание: иногда перечисленными терминами называют точки «икс-игрек», лежащие непосредственно на САМОМ ГРАФИКЕ функции.
Сколько может быть экстремумов у функции?
Ни одного, 1, 2, 3, … и т.д. до бесконечности. Например, у синуса бесконечно много минимумов и максимумов.
ВАЖНО! Термин «максимум функции» не тождественен термину «максимальное значение функции». Легко заметить, что значение 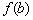
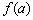
Чайникам на первых порах рекомендую создать и осмыслить небольшой терминологический конспект, чтобы не путать Иран с Ираком.
Подытожим наш небольшой экскурс в теорию контрольным выстрелом: что подразумевает задание «найдите промежутки монотонности и точки экстремума функции»?
Формулировка побуждает найти:
– интервалы возрастания/убывания функции (намного реже фигурирует неубывание, невозрастание);
– точки максимума и/или точки минимума (если таковые существуют). Ну и от незачёта подальше лучше найти сами минимумы/максимумы 😉
Как всё это определить? С помощью производной функции!
Как найти интервалы возрастания, убывания,
точки экстремума и экстремумы функции?
Многие правила, по сути, уже известны и понятны из урока о смысле производной.
Рассмотрим дифференцируемую на некотором интервале функцию 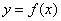
– если производная 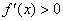
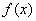
– если производная 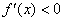
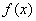
Примечание: справедливы и обратные утверждения.
Пусть точка 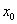
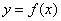
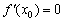
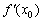
Но сначала потренируемся на кошках разделаемся с простейшими примерами. Почин положен в конце теоретической статьи о производной, и на очереди другие жертвы анализа. Заодно есть возможность провести маленькое самотестирование – насколько хорошо вы запомнили, как выглядят графики жизненно важных функций? В тяжелом случае, конечно же, следует открыть первый урок на соседней вкладке и щёлкать туда-сюда по мере комментариев.
Производная кубической функции 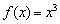
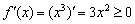
Действительно, кубическая парабола идёт «снизу вверх». Бесконечно близко около точки 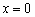
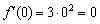
Функция 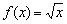
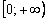
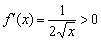
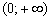
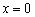
С геометрических позиций тут нет общей касательной. Однако в теории рассматриваются так называемые односторонние производные, и в указанной точке существует правосторонняя производная с правосторонней касательной. Желающие разобраться в этом подробнее могут покурить первый том матана.
Примечание: согласно информации первого параграфа, точка 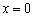
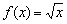
и слева и справа от данных точек. Так же не считаются точками экстремума крайние значения области определения арксинуса и арккосинуса (см. ниже).
Стандартная гипербола 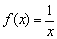
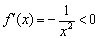
Здесь, к слову, точка 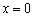
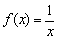
Экспоненциальная функция 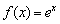
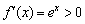
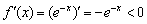
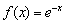
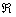
Что делает натуральный логарифм сегодня вечером?
Растёт:
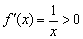
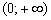
Начертите/распечатайте на соседних либо одном чертеже (иль просто представьте в уме) графики функции 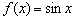
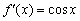
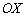
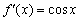
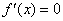
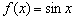
Аналогичная история с косинусом 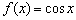
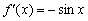
Производная тангенса 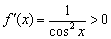
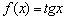
С котангенсом и его производной 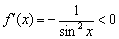
Арксинус на интервале 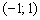
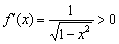
При 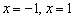
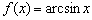
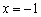
Думаю, вам не составит особого труда провести похожие рассуждения для арккосинуса и его производной.
Все перечисленные случаи, многие из которых представляют собой табличные производные, напоминаю, следуют непосредственно из определения производной.
Зачем исследовать функцию с помощью производной?
Чтобы лучше узнать, как выглядит график этой функции: где он идёт «снизу вверх», где «сверху вниз», где достигает минимумов максимумов (если вообще достигает). Не все функции такие простые – в большинстве случаев у нас вообще нет ни малейшего представления о графике той или иной функции.
Настала пора перейти к более содержательным примерам и рассмотреть алгоритм нахождения интервалов монотонности и экстремумов функции:
Найти интервалы возрастания/убывания и экстремумы функции
Решение:
1) На первом шаге нужно найти область определения функции, а также взять на заметку точки разрыва (если они существуют). В данном случае функция непрерывна на всей числовой прямой, и данное действие в известной степени формально. Но в ряде случаев здесь разгораются нешуточные страсти, поэтому отнесёмся к абзацу без пренебрежения.
2) Второй пункт алгоритма обусловлен
необходимым условием экстремума:
Если в точке 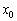
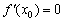
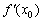
Смущает концовка? Экстремум функции «модуль икс».
Условие необходимо, но не достаточно, и обратное утверждение справедливо далеко не всегда. Так, из равенства 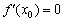
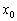
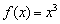
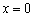
Но как бы там ни было, необходимое условие экстремума диктует надобность в отыскании подозрительных точек. Для этого следует найти производную и решить уравнение 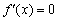
Получилось обычное квадратное уравнение:
Положительный дискриминант доставляет две критические точки:
Примечание: корни можно традиционно обозначить через 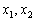
Итак, 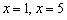
Но экстремумов в них может и не оказаться, поэтому нужно продолжить решение.
первое достаточное условие экстремума,
которое вкратце формулируется следующим образом: пусть функция дифференцируема в некоторой окрестности критической точки 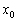
– если при переходе через точку 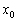
– если при переходе через точку 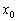
Тут всё очень и очень наглядно, представьте – функция росла-росла-росла, и после прохождения некоторого рубежа вдруг стала убывать. Максимум. Во втором случае график шёл-шёл-шёл «сверху вниз», а при переходе через точку 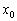
Исходя из вышесказанного, вытекает логичное решение: на числовой прямой нужно отложить точки разрыва функции, критические точки и определить знаки производной на интервалах, которые входят в область определения функции.
В рассматриваемом примере с непрерывностью на 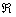
Напрашивается метод интервалов, который уже применялся для определения интервалов знакопостоянства функции. Так почему бы его не использовать для производной? Ведь производная тоже простая смертная функция, найдёшь её – и делай всё, что хочешь.
Внимание! Сейчас мы работаем с ПРОИЗВОДНОЙ, а не с самой функцией!
Перед нами парабола 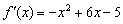

I) Берём какую-нибудь точку интервала 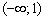
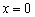
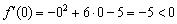
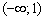
II) Выбираем точку 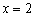
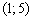
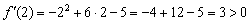
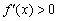
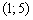
III) Вычислим значение производной в наиболее удобной точке 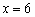
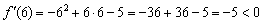
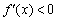
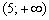
В результате получены следующие знаки производной:

Время собирать урожай!
На интервалах 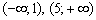
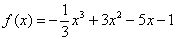
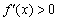
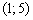
При переходе через точку 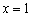
При переходе же через точку 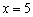
Ответ: функции возрастает на интервале 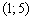
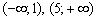
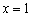
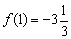
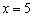
Остерегайтесь сокращенной записи 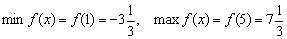
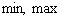
Пример так тщательно провёрнут через мясорубку, что грех не привести графическое изображение всех событий. Незнакомец теоретической части статьи снимает шляпу: 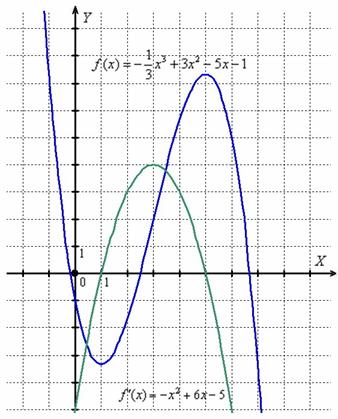
Что произошло? На первом этапе мы нашли производную 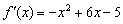
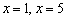
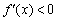
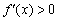
Помимо 1-го достаточного условия экстремума существует и 2-е достаточное условие, однако для исследования функций оно малоинформативно и больше используется в экстремальных задачах.
В начале первой статьи о графиках функции я рассказывал, как быстро построить параболу на примере 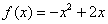
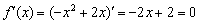
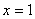
Найти промежутки монотонности и экстремумы функции
Это пример для самостоятельного решения. Полное решение и примерный чистовой образец оформления задачи в конце урока.
Наступил долгожданный момент встречи с дробно-рациональными функциями:
Исследовать функцию с помощью первой производной
Обратите внимание, как вариативно можно переформулировать фактически одно и то же задание.
Решение:
1) Функция терпит бесконечные разрывы в точках 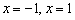
2) Детектируем критические точки. Найдём первую производную и приравняем её к нулю:
Решим уравнение 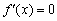
Таким образом, получаем три критические точки:
3) Откладываем на числовой прямой ВСЕ обнаруженные точки и методом интервалов определяем знаки ПРОИЗВОДНОЙ: 
Напоминаю, что необходимо взять какую-нибудь точку интервала, вычислить в ней значение производной 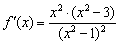
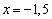
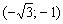
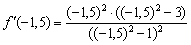
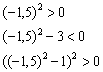
Два «плюса» и один «минус» дают «минус», поэтому 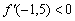
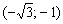
Действие, как вы понимаете, нужно провести для каждого из шести интервалов. Кстати, обратите внимание, что множитель числителя 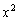
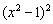
Итак, производная сообщила нам, что САМА ФУНКЦИЯ 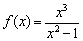
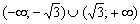
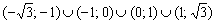
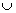
В точке 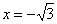
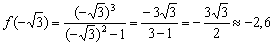
В точке 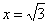
Подумайте, почему можно заново не пересчитывать второе значение 😉
При переходе через точку 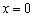
! Повторим важный момент: точки 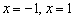
Ответ: функция возрастает на 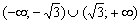
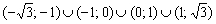
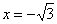
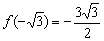
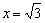
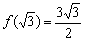
Знание интервалов монотонности и экстремумов вкупе с установленными асимптотами даёт уже очень хорошее представление о внешнем виде графика функции. Человек среднего уровня подготовки способен устно определить, что у графика функции 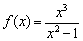
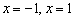
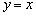
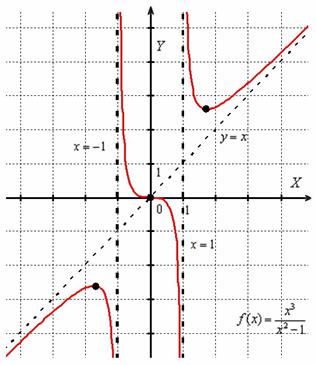
Постарайтесь ещё раз соотнести результаты исследования с графиком данной функции.
В критической точке 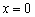
Найти экстремумы функции
Найти интервалы монотонности, максимумы и минимумы функции
…прямо какой-то Праздник «икса в кубе» сегодня получается.
Тааак, кто там на галёрке предложил за это выпить? =)
В каждой задаче есть свои содержательные нюансы и технические тонкости, которые закомментированы в конце урока.
Как отмечалось, в ходе выполнения задания всегда нужно внимательно следить за точками разрыва и интервалами, которые не входят в область определения функции. Казус состоит в том, что иногда производная может существовать на таких участках! Простейший пример: производная натурального логарифма 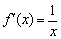
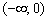
Типичный барьерный риф:
Найти интервалы монотонности и экстремумы функции
Приближаю оформление к боевым условиям и прекращаю нумерацию пунктов алгоритма.
Решение: в Примере 11 статьи об интервалах знакопостоянства была найдена область определения данной функции: 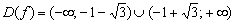
Вроде бы всё хорошо: у нас есть корень 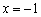
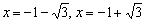
Но производная проявила своеволие – она в отличие от свого родителя определена и на интервале 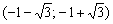
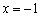

Функция убывает на интервале 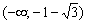
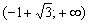
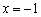
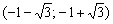
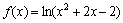
Ответ: функция убывает на интервале 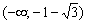
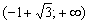
Будьте очень внимательны, если вам встретится логарифм или корень – в подобных примерах просто необходимо увАжить область определения функции!
Найти интервалы монотонности и экстремумы функции
Это приятный разгрузочный пример для самостоятельного решения.
И заключительный пример посвящен другому приключению непослушной дочери:
Найти точки экстремума функции
Решение: функция определена и непрерывна на всей числовой прямой.
Найдём критические точки:
На всякий случай детализирую преобразования знаменателя: 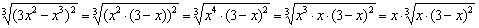
Таким образом, 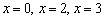
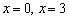
Определим знаки производной на полученных интервалах: 
Функция возрастает на интервале 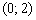
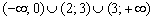
В точке 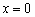
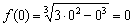
В точке 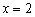
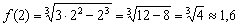
В точке 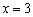
Ответ: 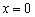
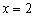
По условию требовалось найти точки экстремума и что-то добавлять излишне. Но в решении как бы невзначай вычислены и сами экстремумы 😉
Давайте посмотрим на на эту оригинальную картину: 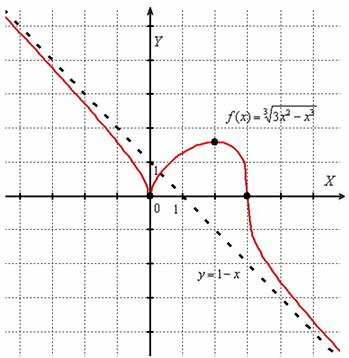
В точке 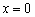
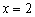
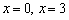
. да, родители и дети бывают разными. Но мама права в 95% случаев с погрешностью 
Пример 2: Решение:
1) Функция определена и непрерывна на всей числовой прямой.
2) Найдём критические точки: 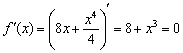
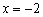
3) Методом интервалов определим знаки производной: 
Ответ: функция убывает на интервале 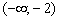
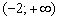
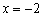
Пример 4: Решение:
1) Функция терпит бесконечный разрыв в точке 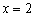
2) Найдём критические точки: 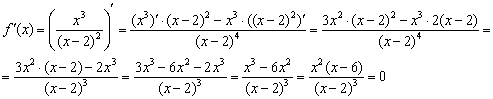
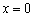
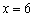
3) Методом интервалов определим знаки производной: 
В точке 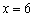
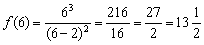
В точке 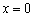
Ответ: в точке 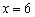
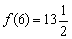
Примечание: обратите внимание, что информацию об интервалах монотонности раскрывать не обязательно, так как по условию требовалось найти только экстремумы функции
Пример 5: Решение:
1) Функция определена и непрерывна на всей числовой прямой кроме точки 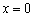
2) Найдём критические точки: 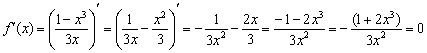
Примечание: в данном случае перед дифференцированием выгодно почленно разделить числитель на знаменатель
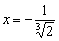
3) Определим знаки производной: 
Ответ: функция возрастает на 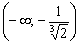
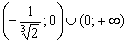
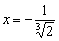
Пример 7: Решение:
Область определения: 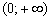
Найдём критические точки: 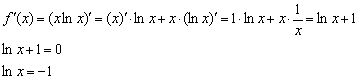
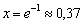
Определим знаки производной: 
Ответ: функция убывает на интервале 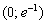
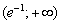
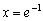
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5