что значит наши прямые стали параллельными

Параллельность прямых

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

Прямая линия. Параллельные прямые. Основные понятия.

Две прямые называются параллельными, если, находясь в одной плоскости, они не пересекаются, сколько бы их ни продолжали. Параллельность прямых на письме обозначают так: AB || СE

Возможность существования таких прямых доказывается теоремой.

Теорема.

Через всякую точку, взятую вне данной прямой, можно провести параллельную этой прямой.

Пусть AB данная прямая и С какая-нибудь точка, взятая вне ее. Требуется доказать, что через С можно провести прямую, параллельную AB. Опустим на AB из точки С перпендикуляр СD и затем проведем СE ^ СD, что возможно. Прямая CE параллельна AB.

Для доказательства допустим противное, т.е., что CE пересекается с AB в некоторой точке M. Тогда из точки M к прямой СD мы имели бы два различных перпендикуляра MD и MС, что невозможно. Значит, CE не может пересечься с AB, т.е. СE параллельна AB.

Следствие.

Аксиома параллельных линий.

Через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой.

Так, если прямая СD, проведенная через точку С параллельна прямой AB, то всякая другая прямая СE, проведенная через ту же точку С, не может быть параллельна AB, т.е. она при продолжении пересечется с AB.

Доказательство этой не вполне очевидной истины оказывается невозможным. Ее принимают без доказательства, как необходимое допущение (postulatum).

Следствия.

1. Если прямая (СE) пересекается с одной из параллельных (СВ), то она пересекается и с другой (AB), потому что в противном случае через одну и ту же точку С проходили бы две различные прямые, параллельные AB, что невозможно.

2. Если каждая из двух прямых (A и B) параллельны одной и той же третьей прямой (С), то они параллельны между собой.

Действительно, если предположить, что A и B пересекаются в некоторой точке M, то тогда через эту точку проходили бы две различные прямые, параллельные С, что невозможно.

Теорема.

Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой параллельной.

Перпендикуляр EF, пересекаясь с AB, непременно пересечет и СD. Пусть точка пересечения будет H.

Предположим теперь, что СD не перпендикулярна к EH. Тогда какая-нибудь другая прямая, например HK, будет перпендикулярна к EH и, следовательно через одну и ту же точку H будут проходить две прямые параллельные AB: одна СD, по условию, а другая HK по доказанному раньше. Так как это невозможно, то нельзя допустить, что СВ была не перпендикулярна к EH.

Источник

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Параллельные прямые: основные сведения

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

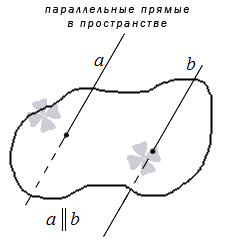
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

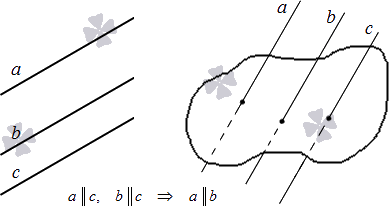
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

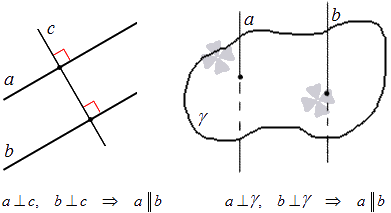
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

A 1 = t · A 2 B 1 = t · B 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

a x = t · b x a y = t · b y

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Решение

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Решение

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

Источник

Наши параллельные стали прямыми

Пять мифов о геометрии Лобачевского

Миф первый. Геометрия Лобачевского не имеет ничего общего с Евклидовой.

На самом деле геометрия Лобачевского не слишком сильно отличается от привычной нам Евклидовой. Дело в том, что из пяти постулатов Евклида четыре первых Лобачевский оставил без изменения. То есть он согласен с Евклидом в том, что между двумя любыми точками можно провести прямую, что ее всегда можно продолжить до бесконечности, что из любого центра можно провести окружность с любым радиусом, и что все прямые углы равны между собой. Не согласился Лобачевский только с пятым, наиболее сомнительным с его точки зрения постулатом Евклида. Звучит его формулировка чрезвычайно мудрено, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.

Миф второй. В теории Лобачевского параллельные прямые пересекаются

Это не так. На самом деле пятый постулат Лобачевского звучит так: «На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную». Иными словами, для одной прямой можно провести как минимум две прямые через одну точку, которые не будут ее пересекать. То есть в этом постулате Лобачевского речи о параллельных прямых вообще не идет! Говорится лишь о существовании нескольких непересекающихся прямых на одной плоскости. Таким образом, предположение о пересечении параллельных прямых родилось из-за банального незнания сути теории великого российского математика.

Миф третий. Геометрия Лобачевского — единственная неевклидова геометрия

Неевклидовы геометрии — это целый пласт теорий в математике, где основой является отличный от Евклидова пятый постулат. Лобачевский, в отличие от Евклида, к примеру, описывает гиперболическое пространство. Существует еще теория, описывающая сферическое пространство — это геометрия Римана. Вот в ней-то как раз параллельные прямые пересекаются. Классический тому пример из школьной программы — меридианы на глобусе. Если посмотреть на лекало глобуса, то окажется, что все меридианы параллельны. Меж тем, стоит нанести лекало на сферу, как мы видим, что все ранее параллельные меридианы сходятся в двух точках — у полюсов. Вместе теории Евклида, Лобачевского и Римана называют «три великих геометрии».

Миф четвертый. Геометрия Лобачевского не применима в реальной жизни

Напротив, современная наука приходит к пониманию, что Евклидова геометрия — лишь частный случай геометрии Лобачевского, и что в реальный мир точнее описывается именно формулами русского ученого. Сильнейшим толчком к дальнейшему развитию геометрии Лобачевского стала теория относительности Альберта Эйнштейна, которая показала, что само пространство нашей Вселенной не является линейным, а представляет собой гиперболическую сферу. Между тем, сам Лобачевский, несмотря на то, что всю жизнь работал над развитием своей теории, называл ее «воображаемой геометрией».

Миф пятый. Лобачевский первым создал неевклидову геометрию

Это не совсем так. Параллельно с ним и независимо от него к подобным выводам пришли венгерский математик Янош Бойяи и знаменитый немецкий ученый Карл Фридрих Гаусс. Однако труды Яноша не были замечены широкой публикой, а Карл Гаусс и вовсе предпочел не издаваться. Поэтому именно наш ученый считается первопроходцем в этой теории. Однако существует несколько парадоксальная точка зрения, что первым неевклидову геометрию придумал сам Евклид. Дело в том, что он самокритично считал свой пятый постулат не очевидным, поэтому большую часть из своих теорем он доказал, не прибегая к нему.

Источник статьи: http://rg.ru/2014/02/07/geometria-site.html

Мы существуем на перекрестке времен и иногда даже чувствуем это

Миры параллельные и перпендикулярные

Об авторе: Юрий Александрович Гуллер – литератор, член Московского союза писателей.

Когда-то писатели-фантасты придумали гипотезу параллельных миров, которые существуют рядом с нами. Иллюстрация Depositphotos/PhotoXPress.ru

Когда-то писатели-фантасты придумали гипотезу параллельных миров, которые существуют рядом с нами, но к которым мы в обыденной жизни не можем даже прикоснуться. Они подобны нашему миру, но или опережают нас по времени, или отстают от нас, в них возможно даже то, что у нас так и не случилось…

Потом к писателям присоединились и ученые. Во всяком случае, изрядная их часть. Параллельные миры существуют, и там есть мы (если мы сумели или успели там родиться) и все то, что есть у нас. И то, чего у нас нет. Только в других, странных сочетаниях. Параллельные миры никогда не пересекаются в отличие от параллельных прямых (если верить Лобачевскому). Они не мешают и не помогают друг другу. Они просто есть. Где-то там…

А если представить себе, что, кроме миров параллельных, есть еще миры, перпендикулярные нашему? Они, как и мы, несутся по предназначенному им пути во времени и пространстве, но однажды в намеченной кем-то точке «Х» наши пути пересекутся друг с другом. А может быть, это произойдет совершенно случайно, в соответствии с тем правилом, что все невозможное однажды может стать возможным? Что случится с этими мирами – и нашим, и перпендикулярным? Они разбегутся, не заметив случившегося, вздрогнут, но выдержат или разлетятся вдребезги по причине полного антагонизма?

А если столкновение, пересечение двух перпендикуляров все-таки произошло? Может быть, именно тогда и возникают на Земле эпидемии, вулканы выплескивают содержимое недр на поверхность, гремят раскаты страшных бурь и всяческих революций, от непонятных причин гибнут целые цивилизации? Отчего пал Древний Рим, сгинула в болоте времени античная цивилизация Древней Греции, оставив после себя только развалины, или вымерли в конце мезозоя динозавры? Предположение, наверное, не слишком научное, но все же, все же, все же…

Быть может, когда происходит пересечение двух перпендикуляров, на Земле возникают катаклизмы и гибнут цивилизации? Пьер-Анри де Валансьен. Извержение Везувия. 1813. Музей августинцев (Тулуза,Франция)

Впрочем, перпендикулярный мир всегда с нами. Мы иногда сталкиваемся лбами с соседом по жизни, с коллегой по работе не в силах ни понять, ни уступить друг другу. Иногда и повода-то особого нет, но все равно – лоб в лоб, так что искры из глаз летят! Кто-то говорил, что в таких огненных спорах и рождается истина. А по-моему, она там как раз и погибает! Человек нам симпатичен, но он все равно существует для нас в другом мире; мы видим и симпатизируем только внешним проявлениям чувств. А кто-то нам неприятен, и каким бы порядочным его ни считали другие, он – не для нашего мира, он «не наш»! Симпатия и антипатия – может быть, это и есть наши с вами параллельные и перпендикулярные миры?

Всегда ли мы можем понять идущего рядом с нами по дороге человека? Он параллелен нам или перпендикулярен? Мы общаемся, ведем долгие беседы, делимся новостями, вместе пьем пиво и вкушаем разные земные радости. Но при этом мы параллельны друг другу, каждый из нас живет в своем мире, в своей жизненной плоскости, и самое глубокое сожаление об утрате (по разным причинам) соседа, друга, даже любимого человека не может остановить течение нашей жизни – оно продолжается!

Наш параллельный мир живет по своим автономным законам и даже по своим календарям. Мы живем с кем-то не один десяток лет. Спим в одной постели, едим за одним столом, живем на одну приличную зарплату, сложенную из двух не совсем приличных. И думаем, что мы – единое целое, разделенное пополам. А от множества «перпендикулярных» отталкиваемся, не желая усложнять простую и понятную картину мира.

Хотя, может быть, именно встреча с «перпендикулярным» тебе человеком и есть то, что должно случиться в каждой жизни, чтобы она обрела и смысл, и звук, и вкус? Это трудно понять, этому трудно следовать. «Мы слишком разные, мы не подходим друг другу», – говорят влюбленные и разбегаются в разные стороны. «Ты меня совсем не понимаешь!» – говорим мы другу, оставляя для общения только редкие телефонные звонки по еще более редким в нашей жизни праздникам. Мы пытаемся понять логику политических событий, но она все равно остается за пределами рассуждений, за понятными нам границами надежд и страхов перед будущим…

Здесь наглядно видно, как «складывается» архитектура в параллельном мире. Кадр из фильма «Начало». 2010

Перпендикулярный мир жесткий и хрупкий; он может разлететься на мелкие осколки, как сказочное зеркало в руках тролля, и осколки разлетятся по миру, раня нам подобных. А может устоять, покрыться трещинами, но устоять. А может даже уничтожить вас. Перпендикулярный мир всегда из антивещества, даже если он живет по законам нашего обычного мира, в согласии с физическими константами, известными из школьного курса. С этим сталкиваются не все, но сколько жертв в истории от таких столкновений! Когда-то, в одном давнем стихотворении у меня промелькнули такие строки: «Черствеет в мышеловке сыр;/ храпит чиновник титулярный…/ Мой жесткий,/ перпендикулярный,/ мой скорый на расправу мир. »

Что делать, если мир перпендикулярен! Но и параллельными миры – «они совсем не для игры». А для чего они, если мы не можем сравнить их с нашим миром и что-то в нем исправить или просто почувствовать себя «на своем месте»?

Мы редко пытаемся анализировать обстоятельства, обступающие нас на каждом шагу. Еще более редко заглядываем внутрь себя и пытаемся понять: мир, в котором мы живем, перпендикулярен нам или это мы ему перпендикулярны? А может быть, это и правильно – жить так, как будто все мы одно целое с миром, нас окружающим? Вопросы, вопросы, вопросы…

Вот, к примеру, попытались мы разобраться с параллельными и перпендикулярными мирами. А получилось ли у нас с вами понять друг друга? Или мы так и остались параллельными жителями множества параллельных миров и планет? Скорее всего именно так. Но может быть, это все-таки лучше, чем сгореть в огненной вспышке аннигиляции при столкновении двух перпендикулярных, сотворенных из вещества и антивещества миров? Во-первых, это жестоко и ни один из нас не пожелает себе таких трагических обстоятельств. А во-вторых, ведь никто не может нам однозначно сказать, что это именно встреченное нами «нечто» (или «некто»), а не мы – то самое «анти», которого мы никак не можем понять и принять?

Оставлять комментарии могут только авторизованные пользователи.

Источник статьи: http://www.ng.ru/style/2021-06-27/8_8183_style.html

Когда параллельные пересекаются

В школьные годы я любила геометрию. Очень долго было для меня неоспоримым фактом, что параллельные прямые не могут пересекаться. Никогда и нигде. Расстояние между ними всегда одинаково, и сколько бы они ни продолжались в пространстве, им не дано встретиться.

А потом я узнала, что кроме геометрии Евклида (откуда, собственно, и получено нами это утверждение) есть другие геометрии. Первое, что я увидела в «альтернативной» геометрии – возможность существования пересечения параллельных прямых. Например, сферическая геометрия на примере земных параллелей и меридианов демонстрирует эту возможность.

Но это все теории и чертежи. Я бы, наверное, и не вспомнила о них, не случись недавно мой разговор с одним другом. Говорили мы о разности людей, о специфике нашего восприятия мира, о коренных отличиях в отношении к одной и той же вещи и понимании ее. Родилось в этом разговоре утверждение, похожее на постулат о параллельных прямых: некоторым людям никогда не удастся найти точки пересечения. Не конфронтации, а соприкосновения, в результате которого может родиться нечто общее. Мы живем как будто на параллельных плоскостях жизни (которые тоже, согласно геометрии Евклида, не имеют общих точек). Мы не согласимся друг с другом никогда.

Никогда – это значит, никогда в жизни. Мы идем по параллельным прямым. Если посмотреть на них вдаль, как на рельсы железнодорожного полотна, то покажется вдруг, что они там, вдалеке, сближаются и соединяются. Но если по этим рельсам ехать, то такого никогда не случится.

Самое интересное, что мир наш при этом один. Он не для каждого свой, он просто воспринимается нами по-разному. Эти параллельные плоскости существуют только в нашем сознании. Как параллельные прямые, бесконечно идущие через пространство, существуют только в математических утверждениях, и на самом деле их в мире нет.
Значит, чтобы наши параллельные прямые и плоскости жизни пересеклись, достаточно просто начать приближаться к объективному видению мира. Но это и есть самое трудное в жизни.

У многих из нас есть ответы на важные вопросы, которые нас устраивают больше всего. Например, каков смысл нашей собственной жизни. Или куда мы пойдем после смерти. Или что такое философия. Получить иной ответ, начать раздумывать над ним означает выбить из-под своих ног привычную твердую почву. Снова искать островки опоры. Идти по зыбкому пути исследования. Перестать быть прямой линией в абстрактном пространстве и начать пересекаться, сталкиваться с другими «линиями» в поиске верного направления. Учиться договариваться, понимать друг друга, вырабатывать общие понятия.

Нам чаще всего неплохо живется на нашей плоскости. Особенно если не сильно задумываться о жизни и мире. Ну, не встретимся мы никогда – и ладно.

Но у нашей планеты есть одна особенность. Она не абстрактный шар, а «неправильное» небесное тело, имеющее неровную поверхность. Если попробовать провести по ней параллельные линии, они обязательно пересекутся. Не через один «виток» вокруг Земли, так через несколько. Так и людские пути рано или поздно пересекаются. Даже самым «крутым» и прямым параллельным суждено однажды встретиться.

Источник