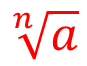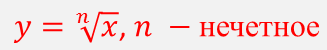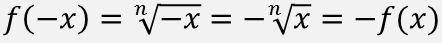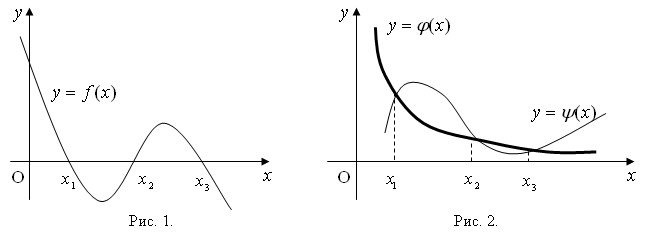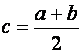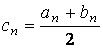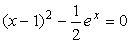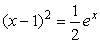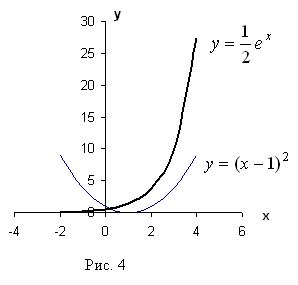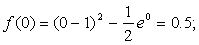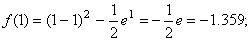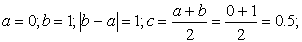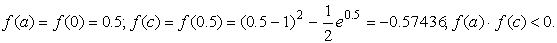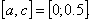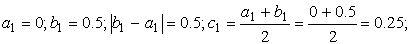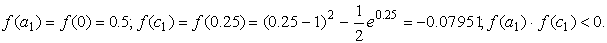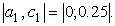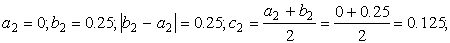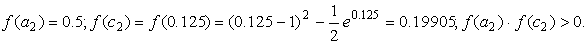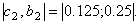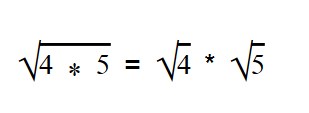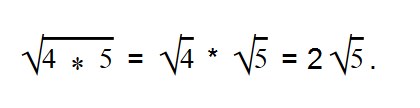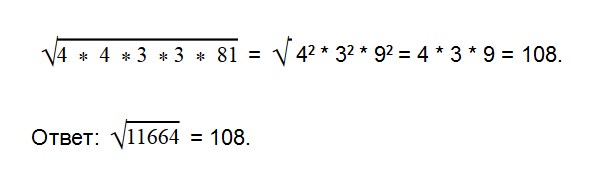что значит найти корни функции

Вычисление корней функции одной переменной

Корнями функции Y=f(x) называют такие значения х, при которых функция принимает значения ноль.

Процесс нахождения корней функции, как правило, осуществляется в два этапа.

На первом этапе отделяются корни, т.е. находятся такие отрезки, внутри которых находится строго один корень.

На втором этапе производится уточнение корней, т.е. находят их значение с заданной точностью ( ). В практических задачах решением является значение х, отличающееся по модулю от точного значения не более чем на величину .

При решении практических задач величина х являются каким-либо ресурсом, величина которого ограничена и лежит в области допустимого диапазона значений. Поэтому при решении задачи интерес представляют только те корни, которые находятся в области возможных значений х.

Отделение корней функции в ограниченной области определения переменной х в табличном процессоре можно выполнить, используя ее табличную или графическую модель.

Для отделения корней функции нужно выполнить следующие операции:

— табулировать функцию, задавая значения аргумента в диапазоне допустимых значений аргумента;

— построить график функции и определить, где находятся точки пересечения графика функции с осью х;

— в полученной табличной модели найти ближайшие приближения к значениям корней. Ближайшими приближениями являются те значения аргумента, в промежутке между которыми значение функции изменяет знак.

1.Выполнить настройку табличного процессора, для этого:

— выполнить команду меню Сервис/Параметры;

— в открывшемся диалоговом окне Параметры выбрать закладке Вычисления;

— в открывшемся диалоговом окне Вычисления установить флажок Итерации, в поле Предельное число итераций установить нужное число итераций, в поле Относительная погрешность ввести величину относительной погрешности вычислений;

— щелкнуть на кнопке ОК.

2. Используя инструмент табличного процессора Подбор параметра, вычислить корни уравнения с заданной точностью.

Рассмотрим технологию вычисления корней функции на примере.

Пример 1.17 Найти все корни функции

Решение

Заданная функция представлена полиномом третьей степени, следовательно, она может иметь не более трех корней.

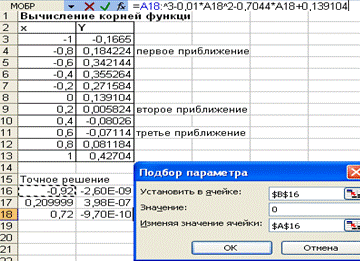
Для локализации начальных приближений определим интервалы значений X, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [-1;+1] с шагом 0,2, получим табличные значения функции. Просмотрев полученную таблицу, находим, что график функции трижды пересекает ось X, следовательно, исходное уравнение имеет на заданном отрезке все три корня.

На свободном участке рабочего листа в диапазон ячеек (А16:А18) введем начальные приближения, а в соответствующие ячейки столбца введем формулу, реализующую функциональную зависимость.

Выполним команду меню Сервис/Параметры, во вкладке Вычисления открывшегося диалогового окна установим относительную погрешность вычислений = 0,000001, а число итераций N = 1000, установим флажок Итерации.

Выполним команду меню Сервис/Подбор параметра. В диалоговом окне заполним следующие поля:

— Установить в ячейке: в поле укажем адрес ячейки, в которой записана формула правой части функции (В16);

— Значение: в поле укажем значение, которому должно удовлетворять значение функции, т.е. правая часть уравнения (в нашем случае 0),

Решение уравнений

Нетрудно догадаться, что решениями уравнения будут корни полученной функции.

Источник

Область определения функции

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие области определения функции

Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.

Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.

Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).

Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.

Из понятия функции сформулируем определение области определения функции.

Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.

Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.

Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.

Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].

Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.

Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:

Например, все действительные числа от 2 до 5 включительно можно записать так:

Все положительные числа можно описать так:

Ноль не положительное число, поэтому скобка возле него круглая.

Области определения основных элементарных функций

Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.

На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.

Рассмотрим области определения основных элементарных функций.

Область определения постоянной функции

Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.

Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.

Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.

Область определения функции с корнем

Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.

Рассмотрим две вариации такой функции.

Область определения корня зависит от четности или нечетности показателя:

Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).

Пример

Найти область определения функции:

Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.

Разложим квадратный трёхчлен на множители:

Дискриминант положительный. Ищем корни:

Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).

Область определения степенной функции

Область определения степенной функции зависит от значения показателя степени.

Перечислим возможные случаи:

Рассмотрим несколько примеров.

Область определения показательной функции

Область определения показательной функции — это множество R.

Примеры показательных функций:

Область определения каждой из них (−∞, +∞).

Область определения логарифмической функции

Логарифмическая функция выглядит так: y = log_ax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.

Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:

Рассмотрим примеры логарифмических функций:

Область определения этих функций есть множество (0, +∞).

Пример

Укажите, какова область определения функции:

Составим и решим систему:

Область определения тригонометрических функций

Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.

Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и x ∈ r, x ≠ πk, k ∈ Z соответственно.

Пример

Найдите область определения функции f(x) = tg2x.

Так как a(x) = 2x, то в область определения не войдут следующие точки:

Перенесем 2 из левой части в знаменатель правой части:

В результате . Отразим графически:

Ответ: область определения: .

Область определения обратных тригонометрических функций

Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.

Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.

Таблица областей определения функций

Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.

И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.

Функция

Область определения функции

Источник

Функции корня.

Корнем n-степени из неотрицательного числа a является такое неотрицательное число, при возведении в n-степень которого получается число a.

Корнем нечетной n-степени из отрицательного числа a называется такое отрицательное число, при возведении в n-степень которого получается число a.

Где n – это показатель корня и a – подкоренное число.

Таким образом, извлечь корень любой степени (от второй и далее) можно из любого неотрицательного числа, а из отрицательного числа извлекается только корень нечетной степени.

На [0; +∞) можно поставить каждому числу х в соответствие единственное число корень n-степени из x при любом значении n.

То есть это означает, что на множестве [0; +∞) можно говорить о функции корня:

Теперь определим свойства данной функции и построим ее график.

Основные свойства функции:

Промежуток [0; +∞) – является областью определения.

Так как неотрицательное число является корнем n-степени из неотрицательного числа, значит промежуток [0; +∞) будет областью значения функции.

Поскольку симметричным множеством не является область определения функции, поэтому данная функция не является ни нечетной, ни четной.

Операция по извлечению корня вводилась как обратная операция возведения в соответствующую степень.

Значит можно утверждать, что:

Теперь можно построить график функции корня.

Пользуясь графиком, можно записать оставшиеся свойства функции.

На промежутке [0; +∞) функция возрастает.

На всей области определения функция выпукла вверх.

У функции наименьшим значением будет являться 0, а наибольшего значения она не имеет.

Если в каждой из точек некоторого промежутка функция дифференцируема, то это значит, что на данном промежутке она непрерывна.

В любой точке промежутка [0; +∞) существует эта производная, исключением является только точка 0. Поскольку в любой точке промежутка (0; +∞) функция имеет производную, значит на промежутке (0; +∞) функция дифференцируема.

Эти примеры касаются функции, у которой у равно корень n-степени из x, только при неотрицательных значениях аргумента.

Но если n является нечетным числом, то для отрицательных х также имеет смысл выражение корень n-степени из x. А значит, говорить можно о функции:

Запишем свойства данной функции.

Промежуток (– ∞; + ∞) является областью определения функции.

Промежуток (– ∞; + ∞) будет областью значений.

Область определения функции является симметричным множеством, значит данную функцию можно исследовать на четность:

Таким образом получаем, что функция будет нечетной при нечетном n.

Построим график функции.

Добавим к этой ветви еще ветвь, которая симметрична ей относительно начала координат, для этого воспользуемся свойством нечетности функции корня.

Еще несколько примеров графиков функции корня.

Источник

Что значит найти корни функции

1. Приближенное решение нелинейных уравнений

Пусть дано уравнение с одним неизвестным

Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.

Приближенное решение уравнения состоит из двух этапов:

1. Отделение корней, то есть нахождение интервалов из области определения функции f ( x ), в каждом из которых содержится только один корень уравнения (1).

2. Уточнение корней до заданной точности.

Отделение корней можно проводить графически и аналитически.

с точностью ε = 0,0001. Отделим корень графически. Для этого преобразуем уравнение к виду

и построим графики функций (рис. 4):

Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку [0; 1].

Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка [0; 1] имеем:

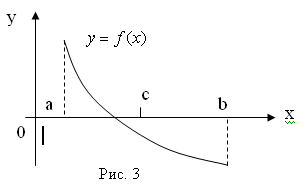
Уточнение корня выполним методом половинного деления.

Корень принадлежит отрезку

Корень принадлежит отрезку

Корень принадлежит отрезку

Источник

Что такое квадратный корень

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое квадратный корень

Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:

Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.

Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0

Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.

Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.

Попробуем найти корень из √-16

Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.

Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.

Числа, стоящие под знаком корня, должны быть положительными.

Исходя из определения, значение корня также не должно быть отрицательным.

Разница между квадратным корнем и арифметическим квадратным уравнением

Прежде всего, чтобы разграничить эти два понятия, запомните:

Это два нетождественных друг другу выражения.

Из выражения x 2 = 16 следует, что:

Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.

В то же самое время, из выражения x = √16 следует, что x = 4.

Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:

Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.

Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.

Даны два выражения:

Первое выражение — квадратное уравнение.

Второе выражение — арифметический квадратный корень.

Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.

Запись иррациональных чисел с помощью квадратного корня

Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.

Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.

Примеры иррациональных чисел:

Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.

Дано уравнение: x 2 = 2.

Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.

Переберем числа, чтобы удостовериться в этом:

1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.

Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.

Извлечение корней

Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.

Таблица квадратов

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Ищем в таблице число 3025.
Влево — 5, вверх — 5.

Ищем в таблице число 7396.

Ищем в таблице число 9025.

Ищем в таблице число 1600.

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

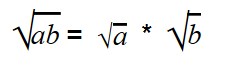Примеры:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

Деление арифметических корней

Для деления арифметических корней используйте формулу:

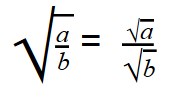Примеры:

Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

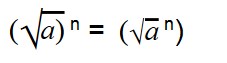Примеры:

Эти две формулы нужно запомнить:

Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Число семь умножено на квадратный корень из числа девять.

Извлечем квадратный корень и умножим его на 7.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня.

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что (√a) 2 = a

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.

Формула внесения множителя под знак корня:

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

Вынесение множителя из-под знака корня

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

Раскладываем подкоренное выражение на множители 28 = 7*4.

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

Ответ: преобразовываем выражение 9√5.

9√5 = √81 * √5 = √81*5 = √405

Ответ: преобразовываем выражение 7√12.

7√12 = √49 * √12 = √49*12 = √588

Это значит, что 7√12 > √20.

Как видите, ничего сложного в сравнении арифметических квадратных корней нет.

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из √2116.

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

Мы видим что, 2116 больше 1600, но меньше 2500.

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

4 2 = 16 ⇒ 6

5 2 = 25 ⇒ 5

6 2 = 36 ⇒ 6

7 2 = 49 ⇒ 9

8 2 = 64 ⇒ 4

9 2 = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Далее вычисляем: 44 * 44 = 1936.

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.

Еще пример. Извлечем корень из числа √11664

Разложим число 11664 на множители:

Запишем выражение в следующем виде:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.

109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10

Источник