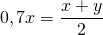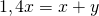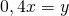что значит найти среднее арифметическое чисел
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.
Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.
Смешанные числа
Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:
Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:
Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.
Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.
Алгоритм нахождения среднего значения
Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.
Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.
Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.
Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.
Методика определения среднеарифметического значения:
Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:
В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.
При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.
Пример решения
Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.
Решение выполняется по следующему алгоритму:
При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.
Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.
Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.
Среднее арифметическое — методы и примеры расчетов
Нахождение среднего арифметического изучается на уроках математики в 5 классе. Однако ученики иногда не понимают эту тему. Изучение материала самостоятельно по учебнику не всегда дает положительный эффект. Специалисты позаботились об этом и разработали специальный алгоритм, который поможет восполнить «пробелы» в знаниях, а также добиться успехов в других физико-математических дисциплинах.
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.
Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.
Смешанные числа
Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:
Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:
Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.
Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.
Алгоритм нахождения среднего значения
Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.
Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.
Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.
Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.
Методика определения среднеарифметического значения:
Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:
В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.
При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.
Пример решения
Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.
Решение выполняется по следующему алгоритму:
При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.
Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.
Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.
Среднее арифметическое: физический смысл и визуализация
Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.
Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.
Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.
Среднее арифметическое двух чисел
Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:
Их среднее арифметическое:
Физический смысл среднего арифметического
Изобразим два исходных числа и их среднее арифметическое на числовой оси:
Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.
В механике момент силы – это произведение силы F на расстояние l:
На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l1 и l2, получим:
Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:
Обозначив m координату точки опоры весов, получим:
Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:
Координата опоры весов m:
Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.
Визуальное восприятие равновесия
Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.
Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.
Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.
Математическое ожидание случайной величины
Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:
Теперь точка опоры весов в равновесии это μ:
Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:
Это и есть формула математического ожидания.
Гистограмма
Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.
На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.
Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:
Дайте мне точку опоры, и я переверну Землю. Архимед
Как найти среднее арифметическое
Как найти среднее арифметическое чисел? Повторим правило и рассмотрим его применение на конкретных примерах.
Чтобы найти среднее арифметическое чисел, надо:
1) сложить эти числа;
2) результат разделить на количество слагаемых:
Найти среднее арифметическое чисел:
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат поделить на 2:
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3:
3) 40,52, 44,63, 52,34 и 58,29.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4:
(40,52 + 44,63 + 52,34 + 58,29):4=48,945.
4) 17,4. 21,6, 25,2, 28,7 и 30,1.
Чтобы найти среднее арифметическое пяти чисел, надо сложить эти числа и результат разделить на 5:
(17,4 + 21,6 + 25,2 + 28,7 + 30,1):5=24,6.
81 Comments
Все ясно,просто моментально вспомнила
Я понял но это не точно
Я ВООБЩЕ ВСЕ ПОНЯЛА. Д/З НА 10 СДЕЛАЛА. ( ПРИМЕРЫ ЛИШНЕЕ )
Если каждую новую тему постараться разобрать сразу же, не откладывая на «когда-нибудь потом», то оказывается, что математика — не такой уж сложный предмет.
Поля, желаю Вам дальнейших успехов в учебе!
Среднее арифметическое 4 чисел равно 7.6, а среднее арифметическое 10 других чисел равно 3.6. Найдите значение среднего арифметического этих 14 чисел. Помогите решить, пожалуйста.
Как найти среднее арифметическое число 5,24
Данил, Вы имеете в виду среднее арифметическое чисел 5 и 24? Чтобы найти среднее арифметическое 5 и 24, надо сумму этих чисел разделить на количество слагаемых: (5+24):2=29:2=14,5.
Количество чисел — три. Чтобы найти среднее арифметическое этих чисел, надо их сложить и сумму разделить на 3: (-3+0+9):3=2.
как найти среднее арифметическое чисел с дробями?
Валерия, так же, как и с другими числами: найти их сумму и разделить на количество слагаемых.
Спасибо за статью!Статья очень помогла!
Непомогло у меня числа
5, 7, 10, 12, 16
Как решить-среднее арифметическое семи чисел равно 10,2,а среднее арифметическое трёх других чисел-6,8.Найдите среднее арифметическое этих десяти чисел.
Валентина, специально в ответ на аналогичный вопрос Вероники написала пост (ссылка вверху, за 27.08.2014)
Спасибо я всё понял
Все довольно понятно, но вся соль в том, что у меня 3 числа — неизвестны. :\
Лол, перепутал. Не правильно прочитал Д/З, спасибо за статью!
Отличная новость, Илья! Поздравляю!
Как и любое другое среднее арифметическое чисел: сложить и поделить на их количество. Если у Вас три числа- (60+75+270)6:3. Если два — (6075+270):2.
среднее арифметическое чисел равно 47.первые три числа равны 37 6 81 найдите четвертое число
Супер!! Оказывается все ОЧЕНЬ легко!! Так мало написанно, но понятно!! 🙂
Среднее арифметическое чисел:
x; 3; 2,1; 2,1
равно 2,55
Найти x
А откуда нужно брать знаменатель?
Делим на количество слагаемых. То есть сколько чисел, среднее арифметическое которых надо найти, дано, на то и делим.
Ребят помогите вот что нам сказали сделать: среднее арефметическое 2 чисел=18.1число=350% второго числа.
Пусть x — I число, тогда II — 3,5x (так как составляет 350% от I-го). Так как их среднее арифметическое равно 18, сосавим и решим уравнение: (x+3,5x):2=18; 4,5x=18∙2; x=36:4,5; x=8. Следовательно, I число равно 8, II — 3,5∙8=28.
Дедушке Вите 90 лет. Средний возраст внуков 20. Среднее арифметическое дедушки и его внуков 22 года. Найдите кол-во внуков. Помогите решить
Пусть n — количество внуков у дедушки. Чтобы найти средний возраст внуков, надо сумму лет всех внуков и разделить на количество внуков, то есть на n. Таким образом, (сумма лет всех внуков):n=20, следовательно,
сумма лет всех внуков=20n.
Чтобы найти средний возраст дедушки и внуков, надо сложить сумму лет всех внуков и дедушки и разделить на (n+1): (сумма лет всех внуков + 90):(n+1)=22.
Значит, (20n + 90):(n+1)=22. Остаётся решить уравнение.
20n + 90=22(n+1)
20n-22n=22-90
n=34.
Ответ: 34 внука.
Повезло деду :D) 34 внука иметь)
Среднее арифметическое восьми чисел равно 4,3. После того как
из этого набора убрали некоторое число, среднее арифметическое
нового набора стало 3,7. Найдите это число. ПОМОГИТЕ РЕШИТ))
1) Среднее арифметическое восьми чисел равно частному от деления суммы этих восьми чисел на 8. По условию, среднее арифметическое этих восьми чисел равно 4,3. Значит, сумма восьми чисел равна 4,3∙8=34,4.
2) Среднее арифметическое семи чисел равно частному от деления суммы семи чисел на 7. По условию, среднее арифметическое семи чисел равно 3,7. Значит, сумма семи чисел равна 3,7∙7=25,9.
3) Разность между суммой восьми чисел и суммой семи чисел и есть то число, которое убрали:
34,4-25,9=8,5.
Спасибо большое все легко и понятно)
Очень благодарна вам и вашему сайту)
Удачи вам в дальнейшем)
Спасибо, Полина! И Вам удачи и успехов в учёбе!
средняя арифметическая 9и чисел равно 16и. если один из этих чисел равен 0 тогда сколько будет ср.арифметическая остальных?
Среднее арифметическое 9 чисел (а1+а2+…+а8+0):9=16.Отсюда а1+а2+…+а8+0=16∙9=144.
Значит, среднее арифметическое оставшихся восьми чисел (а1+а2+…+а8):8=144:8=18.
Среднее арифметическое трёх чисел 15. Найти эти числа, если второе число число в 1,4 раза,а третье в 1.2 раза больше первого.
Пусть первое из чисел равно х, тогда второе — 1,4х, а третье — 1,2х. Так как их среднее арифметическое равно 15, составим и решим уравнение:(х+1,4х+1,2х):3=15.
Светлана Ивановна, если я правильно вас поняла то в моём случае:записать формулу среднего арифметического трёх чисел одно из ко орых в 3 раза больше другого и в 2 раза меньше третьего, это записываем так(х+3х+3х×2):3,заранее спасибо за ответ
Среднее арифметическое двух чисел равно 14 одно из чисел 12,4 как найти другое число
(х+12,4):2=14. Отсюда х=28-12,4=15,6.
Среднее арифметическое двух положительных чисел на 30% меньше большего из этих чисел. На сколько процентов оно больше меньшего из этих чисел? (Ответ запишите числом). Помогите, пожалуйста решить!
Примем большее из данных двух положительных чисел за x, а меньшее — за y. Тогда среднее арифметическое этих чисел равно 0,7x.Имеем:
Отсюда x=y:0,4; x=2,5y. Соответственно, среднее арифметическое 0,7x=0,7∙2,5y=1,75y составляет 175% от меньшего числа y. А значит, среднее арифметическое на 75% больше меньшего из чисел.
Плиз,помогите не могу сообразить.Я считаю показатель с 9 утра до 9 вечера,и с 9 вечера до 9 утра,то есть днём допустим у меня показатель 121руб,а вечером 221,среднее получается 171,но если я беру общий показатель за день,то он 141руб.А как мне из дневного и вечернего показателя высчитать общий?А показатель считается так:Я беру выручку и делю на количество.
Олеся, извините, но я не понимаю, о каком показателе Вы говорите.
Светлана Михайловна доброго времени! Подскажите пожалуйста как определить среднее арифметическое нескольких углов. результат нужен в градусах. Спасибо. Сергей
Наверное, просто найти среднее арифметическое градусных мер и результат округлить до градусов (в 1 градусе 60 минут. Соответственно, до 30 минут округляем с недостатком, от 30 и более — с избытком).
Большое спасибо за ответ.
Здравствуйте, как найти среднее арефметическое в таком примере,с двух сторон не известные числа
Пример: …14,18,25,44,30…
Нужно найти какие цифры нужно вставить по краям
Артём, условие неполное, данных недостаточно.
Здравствуйте помогите найти средеарифметическое двух чисел 1,536 и 1,540
Здравствуйте, не могли бы вы помочь… совсем забыла математику. задача:среднее для серии из 70 значений 30. Какова сумма этих значений?
Среднее арифметическое нескольких чисел равно сумме этих чисел, делённой на количество слагаемых. Следовательно, чтобы найти сумму, надо известное среднее арифметическое умножить на количество слагаемых: 30∙70=2100.
А если в ряду есть отрицательные и положительные числа, как тогда?
среднее арифметическое двух чисел 7,2,чему равна сумма
(a1+a2):2=7,2. Отсюда a1+a2=7,2∙2=14,4.
Я чётка всё поняла это так легко
Не решить у меня числа 1,8;5;7.
Дроби никто не отменял: (1+8+5+7):4=5,25 или 5 1/4.
Здравствуйте как найти среднее арифметическое число 24,35 и 17,69
Сложить и разделить на 2:
(24,35+17,69):2=21,02.
Как найти среднее арифметическое чисел 73;74;83 и а равное 11,4
мне не помогло, у меня с иксом
Денис, значит, у Вас среднее арифметическое известно, и нужно найти одно из чисел. Для этого составьте и решите уравнение.
Помогите решить: 85,37; 49; 63,2; 76,43 найти среднее арефметическое
Среднее арифметическое чисел равно сумме этих чисел, делённой на количество слагаемых: (85,37+49+63,2+76,43):4. Осталось вычислить.
если среднее геометрическое число двух чисел равно 16,а среднее арифметическое равно 20, найдите их?
Пусть эти числа x и y. Среднее арифметическое (x+y):2=20, x+y=40.
Среднее геометрическое √(xy)=16, xy=256. Искомые числа — 32 и 8.