что значит несколько дней это сколько
Что значит несколько дней это сколько
Смотря в какой системе координат 🙂
Смотря в какой системе координат 🙂
У меня такое же представление. Но не помню чтоб где-то этому учили. Опрос коллег по работе вявил, что большинство представляет 2-3 :005:. Хочу узнать, что думает более широкая общественность
уже в прошлом опросе участвовала, но так приятно опять высказаться 🙂
В общем, понятие НЕСКОЛЬКО несет в себе неопределенность и сильно зависит от контекста. Тем не менее, какой-то диапазон все таки обозначается, когда применяется это слово
Внимание, вопрос: «какой числовой диапазон всплываетв вашей голове, когда вы слишите следующие выражения (или любые другие), к примеру: «прошло несколько дней, как он уехал», «подождите несколько минут», «прошло несколько лет. «, «на остановке стояло несколько человек» и т.п.
ЗЫ. Долго лучше не думать ))
Говоря словами Уголовного кодекса, группа-это два и более лиц!
Имя числительное — самостоятельная часть речи, обозначающая число, количество и порядок предметов. Отвечает на вопросы: Сколько? который? какой?
Числительные делятся на три лексико-грамматических разряда: количественные (два, пять, двадцать, пятьдесят, двести, триста пятьдесят один), собирательные (оба, двое, пятеро) и порядковые (первый, второй, сотый). В состав количественных числительных входят определённо-количественные и неопределённо-количественные числительные. Первые обозначают определённое количество единиц (два, четыре, пятнадцать, полтораста, двести), вторые — неопределённое количество единиц; к ним относятся слова мало, немало, много, немного, а также местоименные числительные несколько, сколько, сколько-нибудь, сколько-то, столько.
А тут люди точно знают сколько это. В школе говорили. Родители рассказали.
Хоть где посмотреть-то об этом можно, а то так жизнь моя в невежестве и пройдет?
Что значит несколько дней это сколько
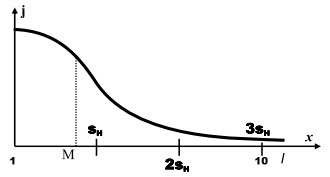
Для начала отметим, что понятие «несколько» применяется к величинам, имеющим очень большой разброс по абсолютной величине. Это могут быть единицы, десятки, тысячи, миллионы штук, или метры, километры, килограммы, тонны. Это могут быть и дробные величины, такие как сантиметры, миллиметры, литры, миллилитры, граммы, миллиграммы и т. д. Поскольку мы пользуемся позиционной системой счисления, то порядок величины может быть вынесен за скобки рассмотрения и служить простым размерным множителем для того отрезка, который мы оцениваем как «несколько». В этом случае удобно воспользоваться логарифмическими представлениями, т. е. использовать логарифмическую шкалу для представления величин. С учётом сказанного, приведём все величины к единому интервалу, базовую величину которого выберем равной основанию (M) используемой позиционной системы счисления. В привычной для нас десятичной системе счисления длина базового интервала будет равна 10 единицам. Он и будет служить нам осью х (смотри рисунок 1).
Рис. 1
Теперь рассмотрим отмеченный выше феномен с инверсией направления изменения верхней границы интервала «несколько» при переходе к миллиону. Человек практически ежедневно и широко пользуется деньгами для покупки товаров и услуг. Наиболее часто он пользуется такими единицами как рубли, десятки и сотни рублей, реже тысячами. Количество людей, пользующихся в своей повседневной практике десятками тысяч рублей и более достаточно мало. Тогда можно проследить следующую тенденцию. Чем выше повседневная потребительская значимость денежной купюры для человека, тем ближе для неё устанавливаются границы значения «несколько» к их математически точному значению. Поскольку миллион для обычного потребителя не является повседневной купюрой, то его повседневная потребительская значимость для человека более абстракция, чем реальность. В этом случаи и границы понятия «несколько» для миллиона устанавливаются скорее как для абстрактного, чем реального объекта, поэтому и оказываются завышенными. А мы-то считали, что ведём опрос на отвлечённых, абстрактных числах и понятиях, а всё свелось подспудно к обыденным денежным знакам, с которыми мы оперируем повседневно. Это следует учитывать при проведении опросов и, особенно, при интерпретации полученных результатов.
Приведённые выше рассуждения о границах понятия «несколько» можно применить к позиционным системам счисления с произвольным основанием. Воспользуемся широко распространённой в вычислительной технике 16-ричной системой счисления. В этом случае длина базового интервала будет равна 16 единицам (от 1 до 16) и поэтому в рассуждениях необходимо использовать логарифмические представления так же по основанию 16. Для функции распределения исходными параметрами будут х0 = 1, sн = 5, тогда математическое ожидание величины «несколько» равно 0,7979sн = 3,9895; дисперсия равна 0,3634(sн) 2 = 9,0850; s = 0,6028sн = 3,0140. При переходе от логарифмического к обычному представлению (не забудем, что логарифм берётся по основанию 16), ответ на поставленный в заголовке материала вопрос будет следующим: понятие «несколько» для 16-ричной системы счисления лежит в диапазоне от 2 до 6. Для системы счисления по основанию 8 (ещё одна система счисления, применяемая в вычислительной технике) получим следующий ответ: от 2 до 3.
несколько
За это время из фирмы уволились несколько сотрудников. | На протяжении двух лет группа записала несколько альбомов. | Он мне звонил несколько раз. | Я привёл несколько версий случившегося.
Саша был несколько озадачен таким холодным приёмом. | В последнее время подход к решению этой проблемы несколько изменился. | Он держался несколько высокомерно.
Смотреть что такое «несколько» в других словарях:
несколько — несколько … Орфографический словарь-справочник
НЕСКОЛЬКО — 1. НЕСКОЛЬКО1, нескольких, числ. Некоторое, неопределенное, весьма ограниченное количество. Рассказать в нескольких словах. За несколько минут до отхода поезда. «Прошептал несколько невнятных слов.» А.Тургенев. 2. НЕСКОЛЬКО2, нареч. (книжн.). В… … Толковый словарь Ушакова
НЕСКОЛЬКО — 1. НЕСКОЛЬКО1, нескольких, числ. Некоторое, неопределенное, весьма ограниченное количество. Рассказать в нескольких словах. За несколько минут до отхода поезда. «Прошептал несколько невнятных слов.» А.Тургенев. 2. НЕСКОЛЬКО2, нареч. (книжн.). В… … Толковый словарь Ушакова
НЕСКОЛЬКО — нареч. неколико, не Бог весть сколько, немного, не очень много, мало. Ведь я несколько взял, и всего то одно беремя. Из этого, кажется, сделано несколько, и народ говорят правильнее. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
НЕСКОЛЬКО — 1. их, числ. неопред. Некоторое, небольшое количество. Н. лет. Рассказать в нескольких словах (кратко). 2. нареч. Немного, отчасти. Сделать н. больше. Н. отвлечься от основной темы. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
несколько — 1. НЕСКОЛЬКО, нескольких, по нескольку; местоим. числ. Некоторое, неопределённое (обычно небольшое) количество. Н. раз. В нескольких местах. Выпить н. глотков. Она прочла н. строк. Уехать на н. недель. Погибло н. сот дельфинов. Можно вас на н.… … Энциклопедический словарь
несколько — 1. по нескольку и (разг.) по несколько. Разместить по нескольку (по несколько) человек в палатках. Еще раз запрещаю вам находиться в цехе неотлучно по нескольку дней (Ажаев). 2. несколько нескольких (вин. падеж в сочетании с существительными… … Словарь управления
несколько — I Р. не/скольких, Д. не/скольким, Тв. не/сколькими, Пр. о не/скольких, числит. Несколько яблок. II нареч. Несколько странный … Орфографический словарь русского языка
несколько — ▲ в количестве ↑ более, один (только) несколько в количестве более одного; два, три или больше; сколько л. объектов; неопределенное число чего л. (в комнате # окон. # слоев. # раз повторить) … Идеографический словарь русского языка
«Несколько» – это сколько? (математическое эссе)
1-10-2010, 13:04 | Наука и техника / Размышления о науке | разместил: VP | комментариев: (0) | просмотров: (9 354)


Тупик Н.В.
Россия, г. Каспийск
С понятием «несколько» мы сталкиваемся ежедневно и повсеместно, но его метрические (количественные) свойства не определены. Для примера зададим вынесенный в заголовок вопрос самому себе, своим знакомым и получим очень интересные результаты. Так, например, на вопрос ««несколько» – это сколько?», мы почти наверняка получим ответ, что «несколько» лежит в диапазоне [(2 – 3), (10 – 15)], т.е. нижняя граница интервала лежит на отметке 2 или 3, а верхняя на отметках от 10 до 15. Если задать этот же вопрос в несколько другой форме: ««несколько сот» – это сколько?», мы с удивлением обнаружим, что верхняя граница интервала значительно сместиться вниз и ответ будет: [(2 – 3), (6 – 7)]. Если ещё более усугубить вопрос и задать его в следующей форме: ««несколько тысяч» – это сколько?», то верхняя граница интервала сместиться ещё больше и ответ будет выглядеть так: [(2 – 3), (4 – 5)].
Пойдём дальше и зададим вопрос: ««несколько миллионов» – это сколько?» и вопреки ожиданиям верхняя граница интервала в ответах сместиться в большую сторону и ответ будет примерно такой: [(2 – 3), (5 – 6)]. Пока не будем останавливаться на этом феномене в определении верхней границы интервала, а зададимся вопросом: Можно ли математически точно определить интервал для понятия «несколько»?
Для начала отметим, что понятие «несколько» применяется к величинам, имеющим очень большой разброс по абсолютной величине. Это могут быть единицы, десятки, тысячи, миллионы штук, или метры, километры, килограммы, тонны. Это могут быть и дробные величины, такие как сантиметры, миллиметры, литры, миллилитры, граммы, миллиграммы и т.д. Поскольку мы пользуемся позиционной системой счисления, то порядок величины может быть вынесен за скобки рассмотрения и служить простым размерным множителем для того отрезка, который мы оцениваем как «несколько». В этом случае удобно воспользоваться логарифмическими представлениями, т.е. использовать логарифмическую шкалу для представления величин. С учётом сказанного, приведём все величины к единому интервалу, базовую величину которого выберем равной основанию (M) используемой позиционной системы счисления. В привычной для нас десятичной системе счисления длина базового интервала будет равна 10 единицам.
Он и будет служить нам осью х (смотри рисунок 1).
Отметим, что в начале оси стоит не 0, а 1, а в конце оси 10, но ось при необходимости может быть продолжена и за эту отметку. К данному интервалу может быть применён любой масштабный коэффициент, это не меняет сути этого интервала и свойств отложенных на нем величин. Например, в системе СИ, если масштаб-ный коэффициент имеет значение 100 – то это могут быть метры, тогда 10–3 – миллиметры, 103 – километры, 10–10 – ангстремы, или если 100 – кубические метры, тогда 10–3 – литры, 10–2 – декалитры, 10–6 – миллилитры и т.д. В результате всё сопоставление будет вестись в пределах единого базового интервала, равного основанию системы счисления.
С другой стороны, поскольку понятие «несколько» используется очень широко и в различных контекстах, то можно ожидать, что оно, как случайная величина, должно иметь нормальный закон распределения.
Отметим также, что данное понятие не чувствительно к знаку, и мы вправе считать, что оно одинаково применимо как к тому, что идёт со знаком «плюс», так и к тому, что оценивается со знаком «минус». Поэтому в нашем случае будет правомерным взять в качестве функции распределения случайной величины «несколько» распределение модуля случайной величины, распределённой по нормальному закону [Справочник по вероятностным расчётам, М.: Воениздат, 1970, с.85 – 87]. Данное распределение характеризуется двумя параметрами: центром рассеяния (х0) и средним квадратичным отклонением (sн). Для нашего случая зададим эти величины равными х0 = 1, sн = 3, тогда функция плотности вероятности (j) будет иметь вид, показанный на рисунке. Её математическое ожидание (MO) равно 0,798sн = 2,39, дисперсия равна 0,3634(sн)2 = 3,270, s = 0,6028sн = 1,808. В результате, переходя на базовом интервале от логарифмического масштаба (log(M)) к линейному, получим, что математическое ожидание понятие «несколько» близко к 2 (100,239 = 1,7), а согласно «правилу двух сигм» в 95% случаев понятие «несколько» не превысит величину, равную 4 (100,239+0,362 = 3,99). Таким образом, понятие «несколько» лежит в диапазоне от 2 до 4.
Теперь рассмотрим отмеченный выше феномен с инверсией направления изменения верхней границы интервала «несколько» при переходе к миллиону. Человек практически ежедневно и широко пользуется деньгами для покупки товаров и услуг. Наиболее часто он пользуется такими единицами как рубли, десятки и сотни рублей, реже тысячами. Количество людей, пользующихся в своей повседневной практике десятками тысяч рублей и более достаточно мало. Тогда можно проследить следующую тенденцию.
Чем выше повседневная потребительская значимость денежной купюры для человека, тем ближе для неё устанавливаются границы значения «несколько» к их математически точному значению. Поскольку миллион для обычного потребителя не является повседневной купюрой, то его повседневная потребительская значимость для человека более абстракция, чем реальность. В этом случаи и границы понятия «несколько» для миллиона устанавливаются скорее как для абстрактного, чем реального объекта, поэтому и оказываются завышенными. А мы-то считали, что ведём опрос на отвлечённых, абстрактных числах и понятиях, а всё свелось подспудно к обыденным денежным знакам, с которыми мы оперируем повседневно. Это следует учитывать при проведении опросов и, особенно, при интерпретации полученных результатов.
Приведённые выше рассуждения о границах понятия «несколько» можно применить к позиционным системам счисления с произвольным основанием.
Воспользуемся широко распространённой в вычислительной технике 16-ричной системой счисления. В этом случае длина базового интервала будет равна 16 единицам (от 1 до 16) и поэтому в рассуждениях необходимо использовать логарифмические представления так же по основанию 16. Для функции распределения исходными параметрами будут х0 = 1, sн = 5, тогда математическое ожидание величины «несколько» равно 0,7979sн = 3,9895; дисперсия равна 0,3634 (sн)2 = 9,0850; s = 0,6028sн = 3,0140. При переходе от логарифмического к обычному представлению (не забудем, что логарифм берётся по основанию 16), ответ на поставленный в заголовке материала вопрос будет следующим: понятие «несколько» для 16-ричной системы счисления лежит в диапазоне от 2 до 6.
Для системы счисления по основанию 8 (ещё одна система счисления, применяемая в вычислительной технике) получим следующий ответ: от 2 до 3.
Таким образом, можно сказать, что понятие «несколько» для 16-ричной системы счисления лежит в диапазоне от 2 до 6; для десятичной системы счисления в диапазоне от 2 до 4; для 8-ричной системы счисления – от 2 до 3.
Что значит несколько дней это сколько
Много кто)))И русские есть, и Чехи, и Евреи и даже Украинцы
не считая Чехов всё остальное и у меня есть))))а фамилия чья?
Деда бабуши. по материнской линии
афигеть)))деда бабушки))Евреем был?
смотря о чем речь! от нескольких минут и до нескольких сотен лет!
смотря что имеется в виду, конкретно должно быть сказано что то
смотря про что вопрос на который был получен этот ответ
счас или после взрыва сверхновой на месте Солнца..
никогда. ближайшее время никогда не наступает.
нет. вы похожи на ослика к которому привязали палочку с морковкой и ослик может целый день ходить и никогда не съест морковь))
просто есть люди которые сдерживают обещания, а есть которые нет, в моем случае ближайшее время было 5 дней. а если я говорю ближайшее время это час максимум
да никто не может вам ничего обещать)))никто не знает будет ли биться его сердце через секунду)))о каких обещаниях может идти речь?)))хотите рассмешить бога расскажите ему о своих планах. ))
живу с ним)))и вы))только вы не сознаете кто вы)найдите для начала себя в себе и бога найдете там же. и тогда не будем бросать слова на ветер. а верите вы во что то или нет это все похер. жизнь не зависит от того что вы о ней думаете. можете придти к богу в молитвах и расшибить себе все колени и лбы и не получить ничего. потому что приходите и говорите подари—не дай а подари. он же не продается.