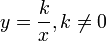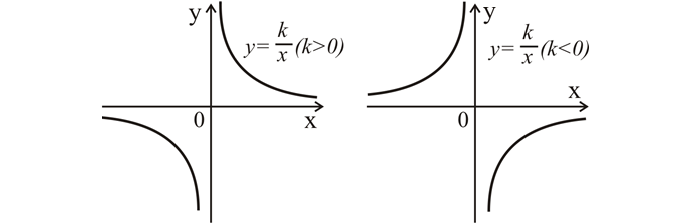что значит обратно пропорционально в физике
Прямая и обратная пропорциональность
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
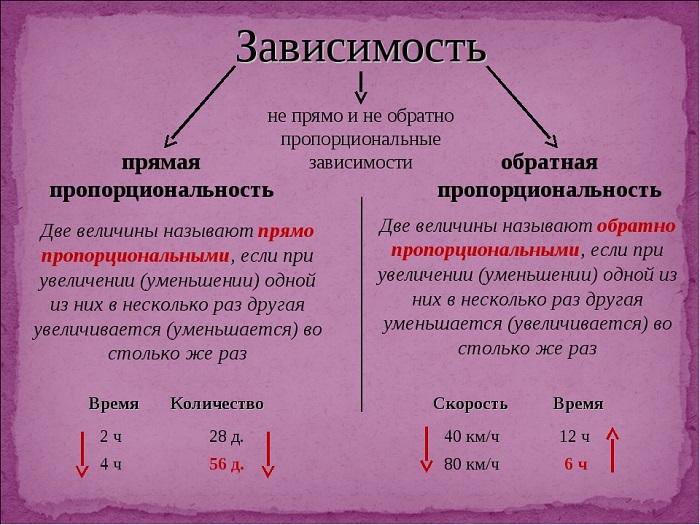
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
Обратная пропорциональность
Содержание
Пример
Масса керосина пропорциональна его объёму: 2 л керосина весят 1,6 кг, 5 л весят 4 кг, 7 л весят 5,6 кг. Отношение массы к объёму всегда будет равно плотности:
1,6 / 2 = 0,8; 4 / 5 = 0,8; 5,6 / 7 = 0,8 и т. д.
Коэффициент пропорциональности
Прямая пропорциональность
Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.
Математически прямая пропорциональность записывается в виде формулы:
Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.
Обратная пропорциональность
Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).
Математически обратная пропорциональность записывается в виде формулы:
См. также
Источники
Полезное
Смотреть что такое «Обратная пропорциональность» в других словарях:
обратная пропорциональность — atvirkštinis proporcingumas statusas T sritis fizika atitikmenys: angl. inverse proportionality vok. umgekehrte Proportionalität, f rus. обратная пропорциональность, f pranc. proportionnalité inverse, f … Fizikos terminų žodynas
ПРОПОРЦИОНАЛЬНОСТЬ — (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова
Пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Содержание 1 Пример 2 Коэффициент пропорциональности … Википедия
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова
пропорциональность — и; ж. 1. к Пропорциональный (1 зн.); соразмерность. П. частей. П. телосложения. П. представительства в парламенте. 2. Матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент пропорциональности. Прямая п. (при которой с… … Энциклопедический словарь
пропорциональность — и; ж. 1) к пропорциональный 1); соразмерность. Пропорциона/льность частей. Пропорциона/льность телосложения. Пропорциона/льность представительства в парламенте. 2) матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент… … Словарь многих выражений
Прямая пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно,… … Википедия
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
МИКРОФОТОГРАФИЯ — МИКРОФОТОГРАФИЯ, получение при помощи светописи изображений микроскоп. объектов, обыкновенно наблюдаемых субъективно через окуляр микроскопа. Основные достоинствам., это точность и объективность даваемых ею изображений, сравнительная быстрота и… … Большая медицинская энциклопедия
Прямая и обратная пропорциональность — формулы, свойства и графики функций
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график
Эта зависимость описывается следующей формулой:
Здесь k и называется коэффициентом пропорциональности.
Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k Свойства функции прямой пропорциональности
Основные свойства следующие:
область определения, значений составляют все действительные числа;
возрастает при всех значениях x, если k > 0;
если коэффициент со знаком «-», т. е. если k 0, то прямая располагается в 1 — 3 координатных четвертях и образует острый угол с осью Х, если k Обратная пропорциональность
Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.
Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).
Функция обратной пропорциональности и ее график
Функция задается формулой:
где k – любое действительное число, кроме 0.
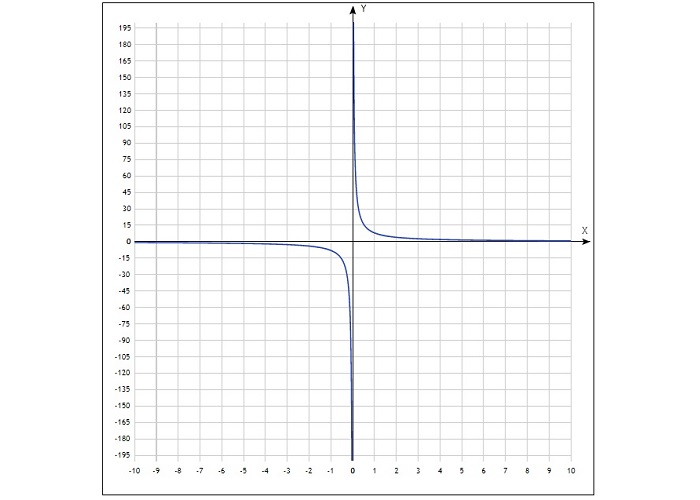
График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
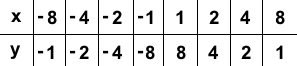
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Свойства функции обратной пропорциональности
области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
оси координат 0х и 0у — это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график
Эта зависимость описывается следующей формулой:
Здесь k и называется коэффициентом пропорциональности.
Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k 0;
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Свойства функции обратной пропорциональности
области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Математика. 6 класс
Конспект урока
Прямая и обратная пропорциональность. Решение задач
Перечень рассматриваемых вопросов:
Равенство двух отношений называют пропорцией.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Теоретический материал для самостоятельного изучения
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.
Столбцы таблицы соответствуют наименованиям зависимых величин.
Строки таблицы соответствуют значениям величин при первом и втором измерении.
Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.
Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?
При постоянном пути скорость и время движения обратно пропорциональны.
Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.
Сделаем краткую запись условия.
Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?
При постоянной скорости путь прямо пропорционален времени движения.
Пусть х м проедет велогонщик за 45 с.
Сделаем краткую запись условия.
Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?
Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?
Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.
Разбор заданий тренировочного модуля
№ 1. Подстановка элементов в пропуски в тексте.
Подставьте нужные элементы в пропуски.
Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?
При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.
Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.
При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.
Пусть х часов – пешеход идёт со скоростью 6 км/ч.
№ 2. Подстановка элементов в пропуски в таблице.
Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.
При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.
Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.