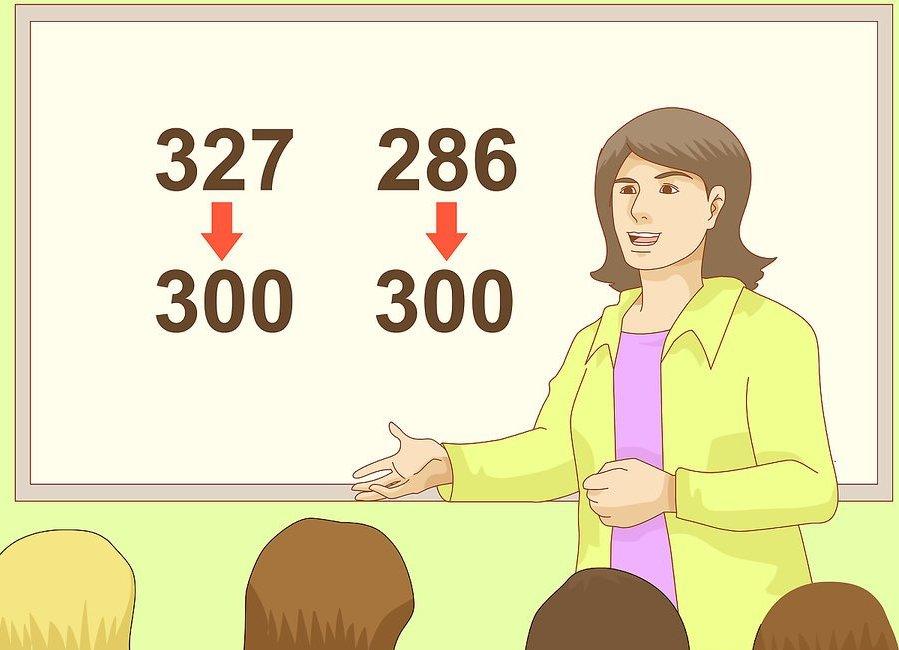
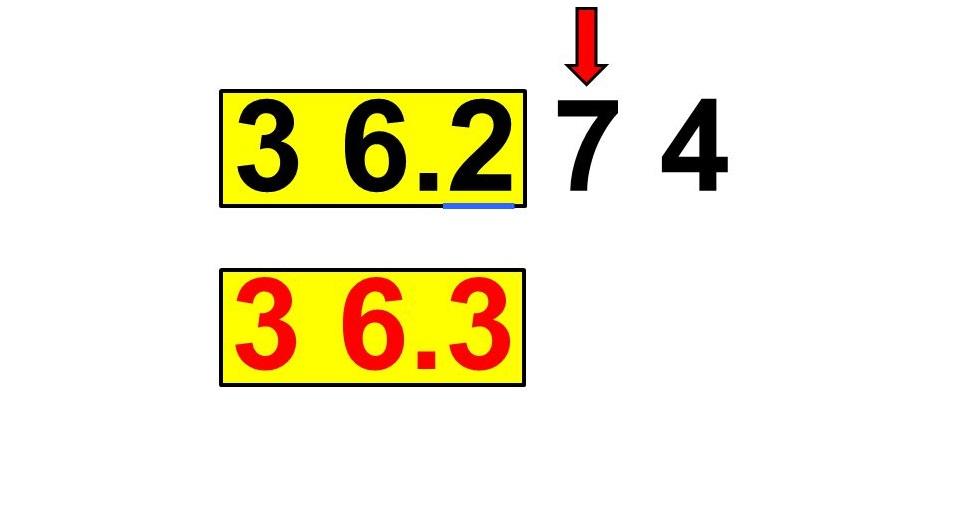
что значит ответ округлите до десятых
Округление десятичных дробей: правила, примеры
В данной публикации мы рассмотрим, каким образом можно округлить десятичные дроби до разных разрядов дробной (десятых, сотых, тысячных и т.д.) и целой (единиц, десятков, сотен и т.д.) частей. Также разберем примеры для лучшего понимания и закрепления материала.
Правила округления десятичной дроби
Десятичную дробь можно округлить:
Но, прежде чем перейти к правилам округления, давайте еще раз вспомним, из чего состоит десятичная дробь. В качестве примера – от тысяч до десятитысячных:
Округление дробной части
Итак, чтобы выполнить округление десятичной дроби, придерживаемся следующего плана действий:
Пример 1: округлим 12,624 до десятых.
Пример 2: округлим 5,176 до сотых.
Округление до целого числа
Если десятичную дробь требуется округлить до целого числа (до единиц), смотрим на цифру, которая идет сразу же после запятой (разряд – десятые). Если это 5, 6, 7, 8 или 9, то к единицам в целой части прибавляем число 1, а всю дробную часть отбрасываем. В остальных случаях просто убираем дробную часть без каких-либо изменений целой части.
Примеры округления десятичных дробей до целого числа:
Примечание: Если дробь требуется округлить до целого числа большего разряда, чем единицы (десятки, сотни, тысячи и т.д.), отбрасываем дробную часть, затем округляем полученный результат согласно правилам округления натуральных чисел.
Пример 1: выполним округление до десятков числа 156,71:
Пример 2: выполним округление до сотен числа 8134,145:
Особый случай: последняя цифра – ноль
Если в результате округления десятичной дроби последней цифрой в дробной части остается 0, его нельзя убирать. Это нужно для того, чтобы наглядно было понято, до какого разряда было выполнено округление.
Примеры округления с нулем на конце
Остановимся подробнее на втором примере. Т.к. в следующем разряде после сотых стоит цифра 9, значит по правилам округления к сотым мы прибавляем единицу: 9 + 1 = 10. Следовательно, в разряде сотых мы пишем ноль, а единицу прибавляем к десятым (1 + 1 = 2).
Как правильно округлить число до десятых
Необходимость округления чисел
Числа округляют в случаях, когда абсолютная точность не нужна или невозможна.

С необходимостью округлять числа до требуемой разрядности для удобства, а порой и для возможности произведения расчетов, сталкиваются не только математики. Человек склонен упрощать себе жизнь, и когда особая точность расчетов не требуется, он, несомненно, округлит любую цифру.
А в случаях, когда в промежуточном расчете получается бесконечная периодическая дробь, то без округления полученного значения дальнейшие расчеты просто невозможны. И единственным выходом остается округление до приемлемой разрядности.
То самое знаменитое «пи» по умолчанию в расчетах принимается с округлением до сотых. Если же в условии задания указано «число п округлите до десятых», то его значение будет 3,1.
При решении задач из школьного учебника точность расчетов принимается по умолчанию до разряда сотых. Если только в условии задачи не указано «округлите числа до разряда десятых».
Округление чисел
Округлением числа называется математическая операция уменьшения количества знаков в числе и замены его приближенным значением заданной точности. Выполняется обнулением значащих цифр справа до заданного разряда. В зависимости от цифры, стоящей в исходном числе после цифры разряда, до которого требуется исключить число, последняя значимая цифра округленного числа может быть равна цифре исходного числа, или увеличена на единицу.
Если первая обнуляемая цифра после цифры заданного разряда меньше или равна 5, то последняя сохраняемая не меняется. Если больше пяти, последняя сохраняемая цифра увеличивается на единицу.
Округление целых чисел
Целое, или натуральное число можно округлять до десятков, сотен, тысяч и так далее. Если натуральное число требуется округлить до десятков, то цифру в разряде единиц заменяют нулем, а цифру в разряде десятков или оставляют без изменения, или увеличивают на единицу, если в исходном числе в разряде единиц была цифра 5 и больше.
Округление дробных чисел
Округление дробных чисел проводится по тем же правилам. Если требуется округлить исходное число до разряда десятых, то в итоговом числе после запятой должна быть одна цифра. Определение, какая именно, аналогично определению последней цифры при округлении натурального числа.
Разберем на примерах.
Пример 1. Как округлить число до десятых?
Пример 2. Как округлить число до десятых?
Исходное число 108,89. Правильным ответом будет 108,9, так как цифра сотого разряда больше пяти. Согласно правилам округления, требуется увеличение предыдущей цифры на единицу.
Пример 3. Как округлить число до десятых?
Исходное число 108,0489. Правильный ответ в этом случае 108,0, так как по правилам округление производится не последовательно, начиная с последней значимой цифры числа, а рассматривается цифра сотого разряда.
Но важно помнить, что, даже если в итоге у вас после запятой получается цифра «0», ее обязательно надо записать, иначе решение будет ошибочным. Без цифры после запятой у вас получится натуральное число, а в условиях задания требовалось округление до разряда десятых.
Пример 4. Как округлить число до десятых?
Исходное число 107,99. Правильный ответ 108,0.
В данном случае цифра ноль после запятой показывает, что число округлено именно до разряда десятых.
Урок 43 Бесплатно Приближенные значения чисел. Округление чисел
Человеку постоянно приходится сталкиваться с решением различных практических и теоретических задач, которые чаще всего связаны с нахождением числовых значений величин.
Измерить какую-либо величину- это значит сравнить ее с однородной величиной, принятой за единицу измерения.
В большинстве случаев полученные значения в результате вычислений и измерений получаются неточными, приближенными: немного больше или меньше истинного значения.
Точность- это степень приближения результата измерения (вычисления) к реальному значению.
Чем меньше точность, тем больше погрешность (расхождение истинного и полученного значения) и, соответственно, чем меньше погрешность, тем выше точность.
Точные измерения проблематичны в реальности по ряду причин:
Так, например, невозможно точно до метра определить протяженность рек, гор, расстояние от Земли до Луны, с точностью до грамма проблематично определить массу грузовика и т.д.
Сегодня на уроке мы научимся находить приближенные значения с избытком и недостатком.
Познакомимся с правилом округления чисел до заданного разряда.
Рассмотрим несколько примеров округления чисел.
Приближенные значения чисел
В настоящее время в различные сферы жизни человека все больше внедряются современные высокоточные устройства, которые позволяют быстро и точно производить измерения и вычисления.
Однако, порой нам даже нет необходимости знать точное значение величины.
Не раз нам приходилось встречать такие фразы: «около одного часа», «примерно один килограмм» или «приблизительно двадцать тысяч рублей» и т.п.
В подобных фразах синонимы: «около», «примерно», «приблизительно» и т.д. указывают на приближенность значений величины, на чуть большее или меньшее значение относительно реального.
Например, говоря о своем возрасте, мы чаще всего называем количество лет и месяцев, не упоминая о прожитых днях и часах.
На вопрос «который час?» мы скорее всего назовем сколько часов и минут в данный промежуток времени, не указывая секунды.
Числа, с которыми нам приходится встречаться и использовать в действительности, бывают двух типов:
Например, говоря о том, что у треугольника 3 стороны, число 3 представляет собой точным числом.
В утверждении о том, что стул имеет 4 ножки, число 4 так же является точным.
На практике, измеряя расстояние, массу, температуру, объем, площадь и другие величины, мы не можем определить их точные значения, а порой эти точные значения вовсе не требуется находить.
Поэтому важно знать (заранее установить) с какой точностью необходимо выполнить измерения и вычисления, т.е. необходимо выяснить какие доли единицы измерения необходимо принять во внимание, а какими можно пренебречь.
Приближенные значения делят на:
Рассмотрим поясняющий пример.
Обратите внимание на рисунок.
Улитка проползла некоторое расстояние и остановилась, данное расстояние обозначим как х (см).
Заметим, что улитка смогла преодолеть больше 7 см, но не смогла доползти до отметки 8 см.
Получается, что расстояние, которое проползла улитка больше 7 см, но меньше 8 см:
Математический язык использует огромное количество специальных символов и знаков, которые однозначно отражают свойства изучаемых процессов, явлений, объектов, освобождают от громоздких записей, конкретны в своей трактовке.
Одним из таких знаков является приближенное равенство.
Приближенное значение указывают с помощью специального знака.
Обозначается данный знак в виде двух волнистых линий: ≈
Знак «приближенное равенство» в 1882 г. предложил немецкий физик-математик Адам Вильгельм Зигмунд Гюнтер.
Запись приближенное равно читается как «приблизительно равно» или «приближенно равно».
Например, a + b ≈ c читается так: сумма a и b приближенно равна с.
Пройти тест и получить оценку можно после входа или регистрации
Округление чисел
Чтобы найти приближенное значение числа, используют математическое действие- округление чисел (замена числа его ближайшим «круглым» числом).
«Круглым» числом называют число, оканчивающееся одним или несколькими нулями.
Округление- это математическая операция, с помощью которой можно уменьшить количество знаков в числе за счет замены этого числа его близким значением с определенной точностью.
Суть операции округления заключается в нахождении числа ближайшего по своему значению к истинному.
Округлить можно любое число до любого разряда.
Важно знать и помнить правильное название и расположение разрядов в числе.
Вспомним разряды десятичных дробей.
Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.
Десятичные дроби возможно округлять так же как натуральные числа до единиц, десятков, сотен, тысяч и т.д.
При округлении числа до десятков число заменяют «круглым» числом, которое должно состоять из целых десятков, а вместо разряда единиц должен быть нуль.
Если необходимо округлить число, например, до сотен, это число заменяют «круглым» числом, в котором остается разряд сотен, а в разряде десятков и единиц должны стоять нули.
Округлим 1,7 до целого.
Рассмотрим процесс округления десятичной дроби с помощью координатного луча.
Разложим заданное число по разрядам.
1,7 = 1 + 0,7
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Отметим на координатном луче точку с координатой 1,7.
Отложим один целый единичный отрезок от начала координат, получим одну целую единицу.
Чтобы отметить дробь 0,7, второй единичный отрезок разделим на десять долей, каждая такая доля будет равна \(\mathbf<\frac<1> <10>= 0,1>\).
От точки с координатой 1 отложим вправо семь долей единичного отрезка ОЕ, получим точку с координатой 1,7.
Обратим внимание, что точка 1,7 находится между натуральными числами 1 и 2.
Точка с координатой 1,7 удалена от точки Е(1) на семь долей единичного отрезка ОЕ, а от точки с координатой 2— всего на три доли единичного отрезка ОЕ.
Таким образом, можно утверждать, что точка с координатой 1,7 расположена ближе к точке с координатой 2.
Значит, при округлении числа 1,7 до целых получается число 2 (1,7 приближенно равно 2).
1,7 ≈ 2
Десятичные дроби так же можно округлять до определенного разряда, стоящего после десятичной запятой: до десятых, сотых, тысячных и т.д.
При округлении до какого-либо разряда все последующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их просто отбрасывают.
Округление чисел происходит по определенному правилу, рассмотрим его.
Чтобы округлить число до какого-либо разряда нужно:
Поясним на примерах.
Пример №1.
Округлим 83421 до сотен.
Подчеркнем в числе цифру 4, так как она стоит в разряде сотен.
83 4 21
За подчеркнутой цифрой стоит цифра 2, следовательно, необходимо действовать согласно Правила №1: оставить цифру 4 без изменения.
Все цифры, стоящие после разряда сотен (цифры 2 и 1), заменим нулями.
В итоге получим округление числа 83 4 21 до 83 4 00.
Результат запишем следующим образом: 83421 ≈ 83400.
Пример №2.
Округлим до разряда единиц число 316,52.
Число 316,52 будем округлять до целых.
Известно, что десятичная дробь состоит из целой части (находящейся до десятичной запятой) и дробной части (находящейся после десятичной запятой).
В заданной десятичной дроби 316,52 в разряде единиц стоит цифра 6.
Подчеркнем цифру 6.
Цифра, стоящая справа от подчеркнутой цифры- это цифра 5, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 6 прибавить единицу.
Получим в разряде единиц цифру 7, все цифры, стоящие следом за округляемым разрядом (стоящие после десятичной запятой), отбрасываем.
Результат запишем следующим образом: 316,52 ≈ 317.
Пример №2.
Округлим число 27,819 до разряда сотых.
В заданной десятичной дроби 27,819 в разряде сотых стоит цифра 1, подчеркнем ее.
27,8 1 9
За подчеркнутым разрядом стоит цифра 9, следовательно, необходимо действовать согласно Правила №2: к подчеркнутой цифре 1 прибавить единицу.
Получим в разряде сотых цифру 2, все цифры, следующие за разрядом сотых, просто отбрасываем.
Результат запишем следующим образом: 27,819 ≈ 27,82.
У меня есть дополнительная информация к этой части урока!
Округлим до тысячных число 1,2397.
В разряде тысячных стоит цифра 9, подчеркнем ее.
1,23 9 7
Справа от подчеркнутой цифры находится цифра 7, значит, необходимо действовать согласно Правила №2: к подчеркнутой цифре 9 прибавить единицу.
9 + 1 = 10
Ноль необходимо оставить в разряде тысячных, а единицу добавить к предыдущему (старшему) разряду, все цифры, стоящие после разряда тысячных нужно просто отбросить.
Получим следующий результат: 1,23 9 7 ≈ 1,240.
Ноль, в полученной десятичной дроби 1,240 оставляем, чтобы показать до какого разряда производилось округление.
Пройти тест и получить оценку можно после входа или регистрации
Как округлять числа в физике
Обработка результатов измерений в лабораториях проводятся на калькуляторах и ПК, и просто удивительно, как магически действует на многих студентов длинных ряд цифр после запятой. «Так точнее» считают они. Однако легко видеть, например, что запись a = 2.8674523 ± 0.076 бессмысленна. При ошибке 0.076 последние пять цифр числа не означает ровно ничего.
Если мы допускаем ошибку в сотых долях, то тысячным, тем более десятитысячным долям веры нет. Грамотная запись результата была бы 2.87 ± 0.08. Всегда нужно производить необходимые округления, чтобы не было ложного впечатления о большей, чем это есть на самом деле, точности результатов.
Правила округления
243.871 ± 0.026 ≈ 243.87 ± 0.03;
243.871 ± 2.6 ≈ 244 ± 3;
1053 ± 47 ≈ 1050 ± 50.
Округление результата измерения достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше 5.
Примеры:
8.337 (округлить до десятых) ≈ 8.3;
833.438 (округлить до целых) ≈ 833;
0.27375 (округлить до сотых) ≈ 0.27.
8.3351 (округлить дл сотых) ≈ 8.34;
0.2510 (округлитьь до десятых) ≈ 0.3;
271.515 (округлить до целых) ≈ 272.
0.875 (округлить до сотых) ≈ 0.88;
0.5450 (округлить до сотых) ≈ 0.54;
275.500 (округлить до целых) ≈ 276;
276.500 (округлить до целых) ≈ 276.
Рефераты и конспекты лекций по географии, физике, химии, истории, биологии. Универсальная подготовка к ЕГЭ, ГИА, ЗНО и ДПА!
Физика – рефераты, конспекты, шпаргалки, лекции, семинары
Правила округления значений погрешностей и результатов измерения
Погрешности измерений показывают также, какие цифры в полученном результате измерения сомнительны, поэтому нет смысла в записи погрешности с большим числом знаков.
По обычаю ограничиваются одной значащей цифрой и только при особо точных измерениях погрешность записывается двумя или тремя цифрами.
Используют 3 правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения:
1. Погрешность результата измерения показывается двумя значащими цифрами, если первая из них 1 или 2, и одной – если первая цифра 3 и более.
2. Результат измерения округляется до того же десятичного разряда, которым заканчивается округления значение абсолютной погрешности.
3. Округление производится только в конечной ответы, а все предварительные расчеты проводят с одним – двумя лишними знаками.
В соответствии с правилом 1 установлены и нормированные значения погрешностей 3В: в числах 1,5% или 2,5% показываются два знака, но в числах 0,5%, 4%, 6%; показывается только один знак.
При округлении результатов измерения используют еще такие правила:
1) лишние цифры в целых чисел заменяют нулями, а в дробных десятичных отвергают; н., 732 «700.
2) если первая из заменяемых нулями или откидываемых цифр 5, то последняя из оставшихся цифр увеличивается на 1;
3) если отвергаем цифра = 5 со следующими нулями, то округление производится до ближнего четного числа.
Результаты измерения можно записать некоторыми значимыми цифрами и рядом нулей, но в этом случае и нули должны полностью определенное значение и характеризуют погрешность измерения. Н., пусть результат измерения их = 9,5 B, который можно записать цифрами: 9,5; 9,50; 9,500. В этих случаях нули после последней значащей цифры определяют показатель достоверности результатов измерения. С этой точки зрения эти записи необходимо читать так: 9,45
Правила записи чисел по СТ СЭВ 543 – 77
1. Значащие цифры данного числа – все цифры от первой слева, не равной нулю, до последней справа. При этом нули, следующие из множителя 10, не учитывают.
а) Число 12,0 имеет три значащие цифры.
б) Число 30 имеет две значащие цифры.
д) 0,0056 имеет две значащие цифры.
3. Различают записи приближенных чисел по количеству значащих цифр.
а) Различают числа 2,4 и 2,40. Запись 2,4 означает, что верны только целые и десятые доли, истинное значение числа может быть, например, 2,43 и 2,38. Запись 2,40 означает, что верны и сотые доли: истинное значение числа может быть 2,403 и 2,398, но не 2,41 и не 2,382.
4. Число, для которого указывают допустимое отклонение, должно иметь последнюю значащую цифру того же разряда, как и последняя значащая цифра отклонения.
а) Правильно: 17,0 + 0,2. Неправильно: 17 + 0,2 или 17,00 + 0,2.
б) Правильно: 12,13 + 0,17. Неправильно: 12,13 + 0,2.
в) Правильно: 46,40 + 0,15. Неправильно: 46,4 + 0,15 или 46,402 + 0,15.
5. Числовые значения величины и её погрешности (отклонения) целесообразно записывать с указанием одной и той же единицы величины.
6. Интервалы между числовыми значениями величин целесообразно записывать:
от 60 до 100, свыше 120 до 150.
Правила округления чисел по СТ СЭВ 543 – 77
1. Округление числа представляет собой отбрасывание значащих цифр справа до определенного разряда с возможным изменением цифры этого разряда.
2. В случае, если первая из отбрасываемых цифр (считая слева направо) менее 5, то последнюю сохраняемую цифру не меняют.
Пример: Округление числа 12,23 до трех значащих цифр дает 12,2.
3. В случае, если первая из отбрасываемых цифр (считая слева направо) равна 5, то последнюю сохраняемую цифру увеличивают на единицу.
Пример: Округление числа 0,145 до двух цифр дает 0,15.
Примечание. В тех случаях, когда следует учитывать результаты предыдущих округлений, поступают следующим образом.
Если отбрасываемая цифра получена в результате округления в меньшую сторону, то последнюю оставшуюся цифру увеличивают на единицу (с переходом при необходимости в следующие разряды).
4. В случае, если первая из отбрасываемых цифр (считая слева направо) более 5, то последнюю сохраняемую цифру увеличивают на единицу.
Пример: Округление числа 0,156 до двух значащих цифр дает 0,16.
Округление выполняют сразу до желаемого количества значащих цифр, а не по этапам.
Пример: Округление числа 565,46 до трех значащих цифр дает 565.
Из книги Л.И. Любимов, И.Д. Форсилова, Е.З. Шапиро
«Поверка средств электрических измерений. Справочная книга».
Ленинград, Энергоатомиздат, Ленинградское отделение, 1987 год
Погрешность результата измерений позволяет определить те цифры результата, которые являются достоверными. Нецелесообразно удерживать в выражении для измеренного значения физической величины большое число цифр, т.к. цифры младших разрядов могут оказаться недостоверными.
Существуют определенные правила округления.
1. В выражении погрешности удерживается не более двух значащих цифр, причем последняя цифра обычно округляется до нуля или пяти. Две цифры следует обязательно удерживать в том случае, когда цифра старшего разряда менее 3.
Пример. 235,732 + 0,15 округляется до 235,73 + 0,15, но не до 235,7 + 0,15.
При промежуточных вычислениях целесообразно, чтобы используемые числа содержали на одну значащую цифру больше, чем будет в окончательном результате. Это позволяет уменьшить погрешность от округления.
3. Если первая из отбрасываемых цифр (считая слева направо) меньше пяти, то остающиеся цифры не меняются.
Пример. 442,749 + 0,4 округляется до 442,7 + 0,4.
4. Если первая из отбрасываемых цифр больше или равна пяти, то последняя сохраняемая цифра увеличивается на единицу.
Пример. 37,268 + 0,5 округляется до 37,3 + 0,5; 37,253 + 0,5 округляется до 37,3 + 0,5.
5. Округление следует выполнять сразу до желаемого числа значащих цифр, поэтапное округление может привести к ошибкам.
Пример. Поэтапное округление результата измерения 220,46 + 4 дает на первом этапе 220,5 + 4 и на втором 221 + 4, в то время как правильный результат округления 220 + 4.
Особенно внимательно нужно относиться к записи результата измерения без указания погрешности (что в общем случае крайне нежелательно). В этом случае в записываемом числе оставляются только те цифры, за достоверность которых можно ручаться, т.е. все значащие цифры записанного числа должны быть достоверными. Значащими цифрами числа считаются все цифры от первой слева, не равной нулю, до последней записанной справа цифры, при этом нули, записанные в виде множителя 10 в степени п, не учитываются. Поэтому записи 2,4 х 10 В в степени 3 и 2400 В не являются тождественными. Первая запись означает, что верны цифры тысяч и сотен вольт и истинное значение может быть, например, 2,42 или 2,38 кВ. Запись 2400 В означает, что верны и единицы вольт, истинное значение может быть 2400,2 или 2390,8 В, но не 2420 или 2380 В.
Из книги П.В. Новицкий и И.А. Зограф
«Оценка погрешностей результатов измерений»
Ленинград, Энергоатомиздат, Ленинградское отделение, 1991 год
стр. 25 1 – 4. ПРАВИЛА ОКРУГЛЕНИЯ ЗНАЧЕНИЙ ПОГРЕШНОСТИ И РЕЗУЛЬТАТА ИЗМЕРЕНИЙ
Рассчитывая значения погрешности, особенно при пользовании электронным калькулятором, значения погрешностей получают с большим числом знаков. Однако исходными данными для расчета являются нормируемые значения погрешности средств измерения, которые указываются всего с одной или двумя значащими цифрами. Вследствие этого и в окончательном значении рассчитанной погрешности должны быть оставлены только первые одна – две значащие цифры. При этом приходится учитывать следующее. Если полученное число начинается с цифр 1 или 2, то отбрасывание второго знака приводит к очень большой ошибке (до 30 – 50 %), что недопустимо. Если же полученное число начинается, например, с цифры 9, то сохранение второго знака, т. е. указание погрешности, например, 0,94 вместо 0,9, является дезинформацией, так как исходные данные не обеспечивают такой точности.
Исходя из этого на практике установилось такое правило: если полученное число начинается с цифры, равной или большей 3, то в нем сохраняется лишь один знак; если же оно начинается с цифр, меньших 3, т. е. с цифр 1 и 2, то в нем сохраняют два знака. В соответствии с этим правилом установлены и нормируемые значения погрешностей средств измерений: в числах 1,5 и 2,5 % указываются два знака, но в числах 0,5; 4; 6 % указывается
В итоге можно сформулировать три правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения.
Расчет погрешности удобнее вести в следующем порядке: сперва необходимо найти абсолютную погрешность, а затем – относительную. Абсолютная погрешность / (Х) = jo X к /100; при jo = 2,5 % и Х к = 300 В это даёт / (Х) = 2,5 х 300 / 100 = 7,5 В
jo = / o x 100 / X = 7,5 x 100 / 267,5 = 2,81 %
При этом более наглядно указать пределы интервала неопределенности измеренной величины в виде Х = (260 – 276) В или 260 В X
Наряду с изложенными правилами округления значений погрешностей результатов измерения иногда предлагаются более обоснованные, но и более сложные правила. Недостаток изложенных правил состоит в том, что относительная погрешность от округления изменяется скачком при переходе, например, от числа 0,29, когда она составляет (0,30 – 0,29) / 0,30 = 3 %, к числу 0,3, когда она будет (0,4 – 0,3) / 0,3 = 30 %. Для устранения столь резкого скачка относительной погрешности округления предлагается каждую декаду возможных значений округляемой погрешности делить на три части: от 0,1 до 0,2, от 0,2 до
Из книги В.А.Кузнецова и Г.В.Ялунина » МЕТРОЛОГИЯ
теоретические, прикладные и законодательные основы «
Москва, Изд – во стандартов, 1998 г.
стр. 215 7.6 Рекомендуемые правила по округлению результатов измерений
Результаты измерений следует округлять по сложившимся правилам. В основе этих правил лежит следующее положение: числовое значение результата измерений представляется так, чтобы оно оканчивалось десятичным знаком того же разряда, какой имеет погрешность этого результата.
Правила округления результата измерений для случаев обычных измерений, не связанных с необходимостью получения высокоточных результатов:
1) погрешность результата измерений представляется с одной или двумя значащими цифрами. Две значащие цифры приводятся в случае выполнения точных измерений;
2) результат измерений округляется так, чтобы он оканчивался цифрой того же разряда, что и значение погрешности. Если числовое значение результата измерения представляется десятичной дробью, оканчивающейся нулями, то нули отбрасываются только до того разряда, который соответствует разряду числового значения погрешности;
3) если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры в
4) если отбрасываемая цифра равна пяти, а следующие за ней цифры неизвестны (отсутствуют) или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная. Число 105,5 при сохранении трех значащих цифр округляют до 106;
5) правила, изложенные в п.1. 4, применяются только при округлении окончательных результатов. Все промежуточные результаты целесообразно представлять тем числом разрядов, которые удается получить