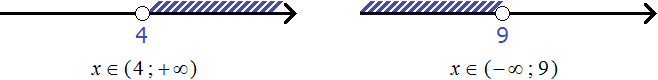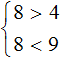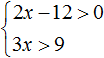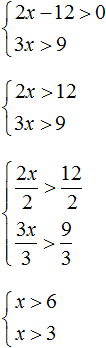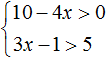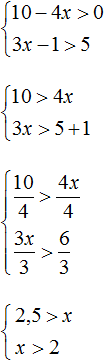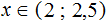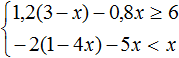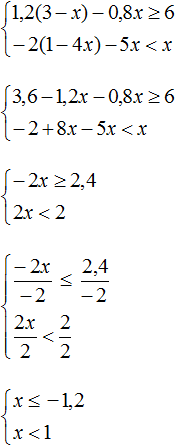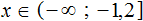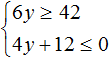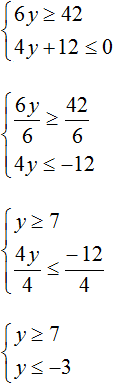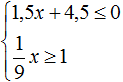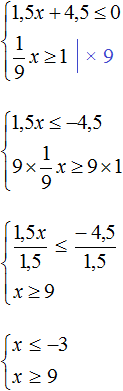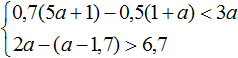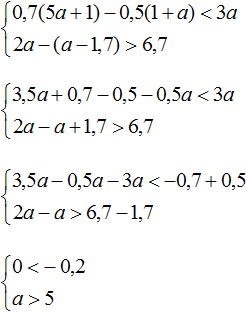что значит решить систему неравенств
Решение систем неравенств
Прежде чем перейти к разбору темы «Как решать систему линейных неравенств» обязательно внимательно изучите урок «Как решать неравенства».
Потренируйтесь в решении неравенств, тогда с системами неравенств у вас не возникнет трудностей.
Системой неравенств называют два или более неравенства, которые объединены фигурной скобкой.
Рассмотрим пример системы неравенств.
Как видно на примере выше, систему неравенств легко определить по фигурной скобке.
Как решить систему неравенств
Чтобы решить систему неравенств нужно:
Вернемся к нашему примеру системы неравенств.
Так как оба неравенства в системе уже решены и представляют собою готовый ответ, то сразу переходим к поиску общего решения всей системы.
Для этого проведем две числовые оси (для каждого из неравенств свою). На осях заштрихуем результат решения неравенств.
Числовые оси с решениями нужно располагать друг под другом.
Числа на осях отмечают в порядке возрастания. То есть число « 2 » будет находиться левее « 5 ».
|  |
После того как мы построили числовые оси с решениями неравенств, необходимо провести через отмеченные на осях числа перпендикулярные прямые.
При проведении прямых через точки на осях соблюдают следующие правила:
Проведем прямые через числовые точки на осях.
Для определения ответа найдем те области решения, которые удовлетворяют ответам обоим неравенствам. Другими словами, те области, где в обоих случаях области решений заштрихованы.
Исходя из полученного анализа, мы получаем, что решением системы неравенств будет « x > 5 ». Запишем полученный ответ.
| |
Рассмотрим другой пример системы неравенств.
Запись двойного неравенства используют, когда интервал решения системы неравенств лежит между числами.
Числа записываются в том же порядке, что они расположены на оси.
Другие примеры решения систем неравенств
В отличии от примеров выше, как правило, в системах неравенств перед поиском общего решения всей системы необходимо предварительно решить каждое из неравенств.
Рассмотрим и решим систему, где неравенства требуют предварительного решения.
Решим линейные неравенства по правилам, описанным в уроке «Решение линейных неравенств». Затем найдем общий ответ системы.
| 5(x + 1) − x > 2x + 2 |
| 4(x + 1) − 2 ≤ 2(2x + 1) − x |
| 5x + 5 − x > 2x + 2 |
| 4x + 4 − 2 ≤ 4x + 2 − x |
| 5x − x + 5 > 2x + 2 |
| 4x + 4 − 2 ≤ 4x + 2 − x |
| 4x + 5 > 2x + 2 |
| 4x + 2 ≤ 3x + 2 |
| 4x − 2x > 2 − 5 |
| 4x − 3x ≤ 2 − 2 |
| 2x > −3 | (:2) |
| x ≤ 0 |
| 2x (:2) > −3 (:2) |
| x ≤ 0 |
x > −
| ||
| x ≤ 0 |
|  |
Ответ: −1
| 1 |
| 2 |
При решении систем неравенств, в которых есть неравенства, содержащие пропорцию, используем правило пропорции.
Системы неравенств
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
Алгоритм решения системы неравенств
Примеры решения систем неравенств:
№1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
Точка 4 на графике жирная, так как знак неравенства нестрогий.
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный.
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
№2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
Точка 3 на графике жирная, так как знак неравенства нестрогий.
Графическая интерпретация решения:
№3. Решить систему неравенств < 3 x + 1 ≤ 2 x x − 7 >5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения:
Графическая интерпретация решения:
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
№4. Решить систему неравенств < x + 4 >0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения первого неравенства:
Решаем методом интервалов.
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 – два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )
Спасибо за просмотр этого урока! Если у вас остались вопросы, напишите их в комментариях.
Математика по полочкам
Готовимся к экзамену по математике за период обучения на II ступени общего среднего образования
13. Системы неравенств
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.
Чтобы решить систему неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это пересечение и является множеством решений системы неравенств.
Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.
Чтобы решить совокупность неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это объединение и является решением совокупности неравенств.
Пример:
Решить совокупность неравенств:
Неравенство. Система неравенств.
Системой неравенств принято называть любую совокупность двух или более неравенств, содержащих неизвестную величину.
Наглядно данную формулировку иллюстрируют, к примеру, такие системы неравенств:
Решить систему неравенств — означает найти все значения неизвестной переменной, при которых реализуется каждое неравенство системы, либо обосновать, что таких не бывает.
Значит, для каждого отдельного неравенства системы вычисляем неизвестную переменную. Далее из получившихся значений выбирает только те, которые верны и для первого и для второго неравенства. Следовательно, при подстановке выбранного значения оба неравенства системы становятся правильными.
Разберем решение нескольких неравенств:
Разместим одну под другой пару числовых прямых; на верхнею нанесем величину x, при которых первое неравенство (x > 1) становиться верным, а на нижней—величину х, которые являются решением второго неравенства (х > 4).
Сопоставив данные на числовых прямых, отметим, что решением для обоих неравенств будет х > 4. Ответ, х > 4.
Как известно таких чисел нет и заданная система неравенств, не имеет решений ни при каких значениях х. Сходные системы неравенств называют несовместными.
Системы линейных неравенств с одной переменной
Примеры решения систем линейных неравенств с одной переменной
Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.
Рассмотрим простейший пример. Система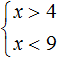 
состоит из двух неравенств, которые уже решены.
Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.
Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:
Но дело в том, что неравенства x > 4 и x соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями, как захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.
Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.
Значит решениями системы 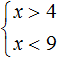являются числа от 4 до 9. Границы 4 и 9 не включаются во множество решений системы, поскольку неравенства x > 4 и x строгие. Ответ можно записать в виде числового промежутка:
Также, нужно изобразить множество решений системы на координатной прямой.
Для системы линейных неравенств решение на координатной прямой изображают так:
Сначала указывают границы обоих неравенств:
На верхней области отмечают множество решений первого неравенства x > 4
Видим, что решение 8 удовлетворяет обоим неравенствам.
Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:
Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.
Пример 2. Решить систему неравенств 
Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.
Решениями же обоих неравенств являются все числа, которые больше 17.
Изобразим множество решений системы 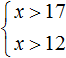на координатной прямой и запишем ответ в виде числового промежутка.
Для начала отметим на координатной прямой границы обоих неравенств:
На верхней области отметим множество решений первого неравенства x > 17
На нижней области отметим множество решений второго неравенства x > 12
Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы 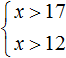. Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:
Пример 3. Решить систему неравенств 
Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок
Получили систему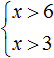 
. На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.
Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства ( x > 6 и x > 3 ). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы
Пример 4. Решить систему неравенств 
Решим каждое неравенство по отдельности:
Изобразим множество решений системы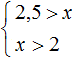 
на координатной прямой и запишем ответ в виде числового промежутка:
Пример 5. Решить неравенство 
Решим каждое неравенство по отдельности:
Изобразим множество решений системы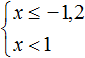 
на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.
Пример 1. Решить неравенство 
Решим каждое неравенство по отдельности:
Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.
Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:
На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система 
А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система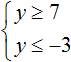
Ответ: решений нет.
Пример 2. Решить систему неравенств 
Решим каждое неравенство по отдельности:
Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:
Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система 
А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система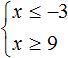
Ответ: решений нет.
Пример 3. Решить систему неравенств 
Решим каждое неравенство по отдельности:
