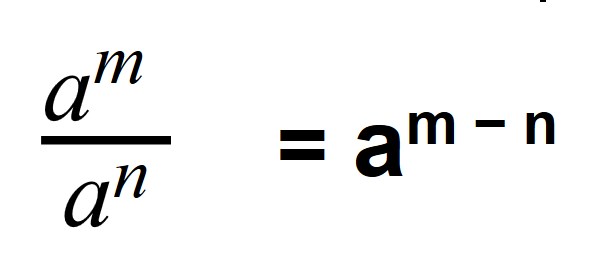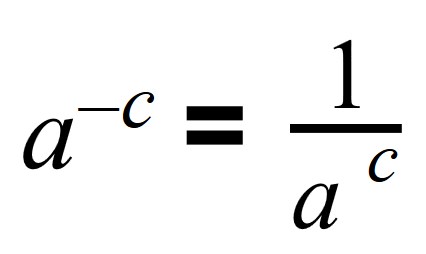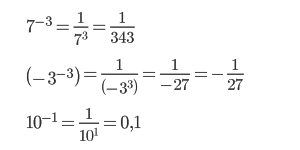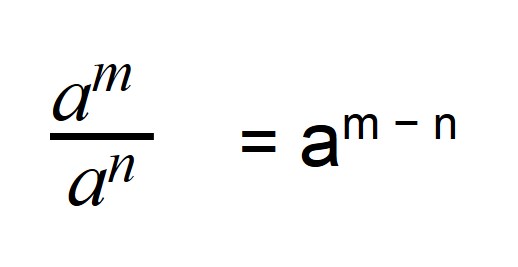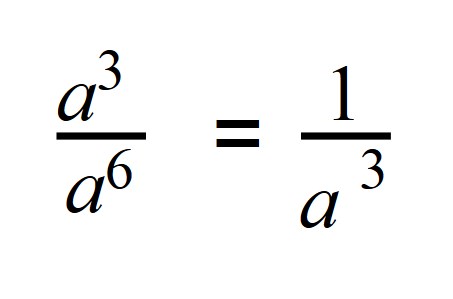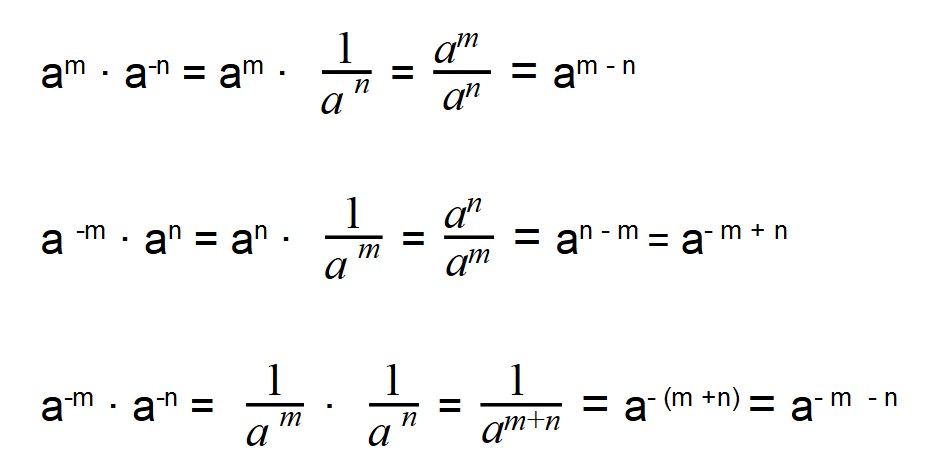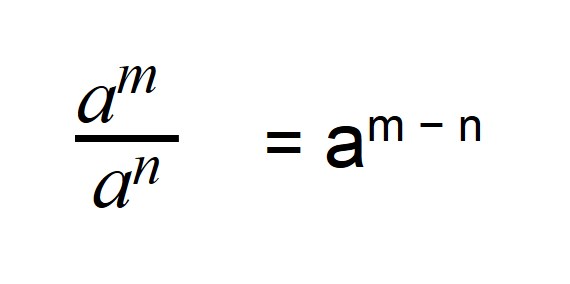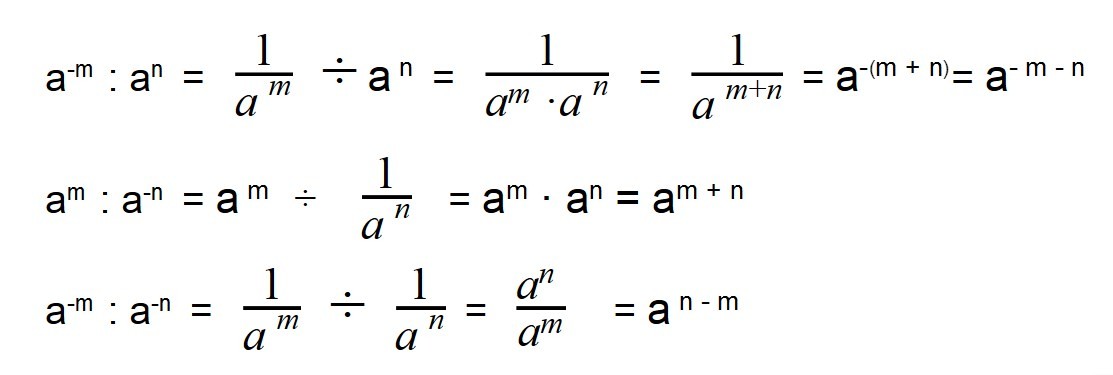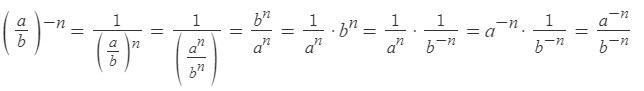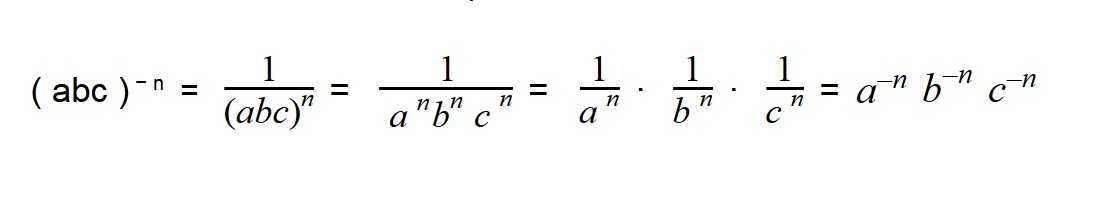что значит секунда в 1 степени
Как перевести секунда в минус первой степени в обороты в минуту?
Умножить на 60. Оборот не является физической величиной, поэтому вместо «оборот/с» пишут просто «1/с», или «с^-1». А поскольку в минуте 60 секунд, то при переводе из «с^-1» в «оборот/мин» и надо умножать на 60.
Ну что же,переведём:
cek^(-1)=1/сек=1/( (1/60)*мин )=1*(60/1)/мин=60/ми н=60*мин^(-1)
Это если записать математически.
Эта секунда в минус первой степени по другому 1 Герц (Гц).Единица измерения частоты.
Если раньше все школы нашей необъятной Родины учились по единому учебнику, то в настоящее время учебников по одному и тому же предмету развелось вагон и маленькая тележка.
Ответы по математике,можно купить решебник в книжном магазине, либо скачать с интернета, либо посмотреть решебники онлайн. Главное чтобы автор учебника, совпал с ответами решебника. Поэтому сначала следует посмотреть создателей учебника.
Математика на экономических специальностях не слишком сложная, в основном статистика.
Что значит секунда в 1 степени
Производные единицы СИ.
ПЕРИОДИЧЕСКИЕ И СВЯЗАННЫЕ С НИМИ ЯВЛЕНИЯ
Фаза колебаний ср — аргумент функции, описывающей величину, изменяющуюся по закону гармонических колебаний. Фаза колебаний не имеет размерности, единица — радиан (rad; рад)
Период Т — интервал времени, в течение которого совершается один цикл периодического процесса; единица — секунда (s, с).
Частота периодического процесса f, v — величина обратная периоду; единица — герц (Hz; Гц).
Герц равен частоте периодического процесса, при которой за время 1 с совершается один цикл периодического процесса.
Частота вращения п — величина, равная числу оборотов, совершаемых за время 1 с; единица — секунда в минус первой степени (s-1; c-1).
Секунда в минус первой степени равна частоте равномерного вращения, при которой за время 1 с тело совершает один полный оборот.
Волновое число v — величина, обратная длине волны, единица — метр в минус первой степени (m-1; м-1).
Метр в минус первой степени равен волновому числу колебаний с длиной волны 1 м.
Коэффициент затухания б — величина, обратная интервалу т, в течение которого амплитуда А уменьшается в е раз; единица — секунда в минус первой степени (s-1; c-1).
Секунда в минус первой степени равна коэффициенту затухания, при котором за время 1 с амплитуда уменьшается в е раз, где е — основание натурального логарифма.
Коэффициент ослабления — величина, характеризующая свойства вещества и равная отношению относительного уменьшения интенсивности dI/I излучений к длине пути ах, пройденного излучением в данном веществе.
Метр в минус первой степени равен коэффициенту ослабления, при котором на расстоянии в 1 м амплитуда уменьшается в е раз, где е — основание натурального логарифма.
Свойства степеней. Действия со степенями
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
a — основание степени;
n — показатель степени.
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
Математики заскучали и решили все упростить:
Ответ: через четыре года у вас будет 81 миллион.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
Когда люди говорят, что им «довольно момента», они наверняка не догадываются, что обещают освободиться ровно через 90 секунд. Ведь в Средние века термин «момент» определял промежуток времени продолжительностью в 1/40 часа или, как тогда было принято говорить, 1/10 пункта, составлявшего 15 минут. Иными словами, он насчитывал 90 секунд. С годами момент утратил свое первоначальное значение, но до сих пор используется в обиходе для обозначения неопределенного, но очень краткого интервала.
Так почему же мы помним момент, но забываем о гхари, нуктемероне или о чем-то ещё более экзотическом?
1. Атом
Слово «атом» происходит от греческого термина, обозначающего «неделимое», и потому используется в физике для определения мельчайшей частицы вещества. Но в старину это понятие применялось по отношению к кратчайшему промежутку времени. Считалось, что минута насчитывает 376 атомов, продолжительность каждого из которых составляет менее, чем 1/6 секунды (или 0,15957 секунды, если быть точным).
2. Гхари
Какие только приборы и приспособления не изобретались в Средние века для измерения времени! Пока европейцы вовсю эксплуатировали песочные и солнечные часы, индийцы применяли клепсидры — гхари. В полусферической чаше, изготовленной из дерева или металла, проделывали несколько отверстий, после чего помещали ее в бассейн с водой. Жидкость, просачиваясь через прорези, медленно наполняла сосуд, пока от тяжести он полностью не погружался на дно. Весь процесс занимал около 24 минут, поэтому такой диапазон и был назван в честь прибора — гхари. В то время считалось, что день состоит из 60 гхари.
3. Люстр
Люстр — это период, длящийся 5 лет. Использование этого термина уходит корнями в античность: тогда люструм обозначал пятилетний отрезок времени, завершавший установление имущественного ценза римских граждан. Когда сумма налога была определена, отсчет подходил к концу, и торжественная процессия высыпала на улицы Вечного города. Церемония заканчивалась люстрацией (очищением) — пафосным жертвоприношением богам на Марсовом поле, совершавшимся ради благополучия граждан.
4. Майлвэй
Не все то золото, что блестит. Тогда как световой год, казалось бы, созданный для определения периода, измеряет дистанцию, mileway, путь длиной в милю, служит для отсчета времени. Хотя термин и звучит как единица измерения расстояния, в раннем Средневековье он обозначал отрезок продолжительностью 20 минут. Именно столько в среднем занимает у человека преодоление маршрута длиной в милю.
5. Нундин
Жители Древнего Рима трудились семь дней в неделю, не покладая рук. На восьмой день, впрочем, считавшийся у них девятым (римляне относили к диапазону и последний день предыдущего периода), они организовывали в городах огромные рынки — нундины. Базарный день получил название «novem» (в честь ноября — девятого месяца 10-месячного земледельческого «Года Ромула»), а временной промежуток между двумя ярмарками — нундин.
6. Нуктемерон
Нуктемерон, комбинация из двух греческих слов «nyks» (ночь) и «hemera» (день), является не более, чем альтернативным обозначением привычных нам суток. Все, что считается нуктемеронным, соответственно, длится менее 24 часов.
7. Пункт
В Средневековой Европе пункт, называемый также точкой, использовался для обозначения четверти часа.
8. Квадрант
А сосед пункта по эпохе, квадрант, определял четверть дня — период продолжительностью 6 часов.
9. Пятнадцать
После нормандского завоевания слово «Quinzieme», переводимое с французского как «пятнадцать», было заимствовано британцами для определения пошлины, пополнявшей казну государства на 15 пенсов с каждого заработанного в стране фунта. В начале 1400-х термин приобрел и религиозный контекст: его стали использовать для указания дня важного церковного праздника и двух полных недель, следующих за ним. Так «Quinzieme» превратился в 15-дневный период.
10. Скрупул
Слово «Scrupulus», в переводе с латыни обозначающее «маленький острый камушек», прежде служило аптечной единицей измерения веса, равной 1/24 унции (около 1,3 гр). В 17 веке скрупул, ставший условным обозначением небольшого объема, расширил свое значение. Он стал применяться для указания 1/60 части круга (минуты), 1/60 минуты (секунды) и 1/60 дня (24 минут). Сейчас, утратив свой былой смысл, скрупул трансформировался в скрупулезность — внимательность к мелочам.
И еще некоторые временные величины:
1 аттосекунда (одна миллиардная миллиардной доли секунды)
Самые быстротекущие процессы, которые способны захронометрировать ученые, измеряют в аттосекундах. С помощью наиболее совершенных лазерных установок исследователи сумели получить световые импульсы длящиеся всего 250 аттосекунд. Но какими бы бесконечно малыми ни казались эти временные промежутки, они представляются целой вечностью по сравнению с так называемым временем Планка (около 10-43 секунды), по мнению современной науки, наикратчайшим из всех возможных временных отрезков.
1 фемтосекунда (одна миллионная миллиардной доли секунды)
Атом в молекуле совершает одно колебание за время от 10 до 100 фемтосекунд. Даже самая быстротекущая химическая реакция протекает за период, исчисляемый несколькими сотнями фемтосекунд. Взаимодействие света с пигментами сетчатой оболочки глаза, а именно этот процесс и позволяет нам видеть окружающее, длится около 200 фемтосекунд.
1 пикосекунда (одна тысячная миллиардной доли секунды)
Самые быстродействующие транзисторы функционируют во временных рамках измеряемых в пикосекундах. Время существования кварков, редких субатомных частиц, получаемых в мощных ускорителях, составляет всего одну пикосекунду. Средняя продолжительность гидрогенной связи между молекулами воды при комнатной температуре равняется трем пикосекундам.
1 наносекунда (миллиардная доля секунды)
Луч света, проходящий через безвоздушное пространство, за это время способен преодолеть расстояние всего в тридцать сантиметров. Микропроцессору в персональном компьютере потребуется от двух до четырех наносекунд, чтобы выполнить одну команду, к примеру, сложить два числа. Время существования К-мезона, еще одной редкой субатомной частицы, составляет 12 наносекунд.
1 микросекунда (миллионная доля секунды)
За это время луч света в вакууме покроет расстояние в 300 метров, длину примерно трех футбольных полей. Звуковая же волна на уровне моря способна за этот же промежуток времени преодолеть расстояние равное всего одной трети миллиметра. 23 микросекунды потребуется для того, чтобы взорвалась динамитная шашка, фитиль которой догорел до конца.
1 миллисекунда (тысячная доля секунды)
Кратчайшее время экспозиции в обычной фотокамере. Всем нам знакомая муха взмахивает своими крылышками один раз в три миллисекунды. Пчела – один раз за пять миллисекунд. С каждым годом луна вращается вокруг Земли на две миллисекунды медленнее, так как ее орбита постепенно расширяется.
1/10 секунды
Глазом моргнуть. Именно это мы успеем сделать за указанный промежуток. Человеческому уху требуется как раз такое время, чтобы отличить эхо от первоначального звука. Космический корабль Voyager 1, направляющийся за пределы солнечной системы, за это время удаляется от солнца на два километра. За десятую долю секунды колибри успевает семь раз взмахнуть своими крылышками.
1 секунда
Сокращение сердечной мышцы здорового человека длится как раз это время. За одну секунду Земля, вращаясь вокруг солнца, покрывает расстояние в 30 километров. За это время само наше светило успевает проделать путь в 274 километра, с огромной скоростью несясь через галактику. Лунный свет за этот временной интервал не успеет достичь Земли.
1 минута
За это время мозг новорожденного ребенка прибавляет в весе до двух миллиграммов. Сердце землеройки успевает сократиться 1000 раз. Обычный человек за это время может произнести 150 слов или прочитать 250 слов. Свет от солнца достигает Земли за восемь минут. Когда же Марс находится на наиболее близком расстоянии от Земли, солнечный свет, отражаясь от поверхности Красной планеты, доходит до нас меньше чем за четыре минуты.
1 час
Столько времени требуется репродуцирующим клеткам, чтобы разделиться пополам. За один час с конвейера Волжского автомобильного завода сходят 150 «Жигулей». Свет от Плутона – самый отдаленной планеты Солнечной системы – достигает Земли за пять часов двадцать минут.
1 сутки
Для людей это, пожалуй, самая естественная единица измерения времени, основанная на вращении Земли. Согласно данным современной науки долгота суток составляет 23 часа 56 минут и 4,1 секунды. Вращение нашей планеты постоянно замедляется из-за лунной гравитации и других причин. Сердце человека за сутки совершает около 100000 сокращений, легкие вдыхают около 11000 литров воздуха. За это же время детеныш голубого кита прибавляет в весе 90 кг.
Земля совершает один оборот вокруг солнца и поворачивается вокруг своей оси 365,26 раза, средний уровень мирового океана повышается на величину от 1 до 2,5 миллиметров, а в России проводятся 45 выборов федерального значения. Потребуется 4,3 года, чтобы свет от ближайшей звезды Proxima Centauri достиг Земли. Примерно столько же времени понадобится на то, чтобы поверхностные океанские течения обогнули земной шар.
1 столетие
1 миллион лет
Космический корабль, летящий со скоростью света, не покроет и половины пути до галактики Андромеда (она находится на расстоянии 2,3 млн световых лет от Земли). Самые массивные звезды, голубые супергиганты (они в миллионы раз ярче Солнца) сгорают примерно за это время. Вследствие сдвигов тектонических пластов Земли, Северная Америка отдалится от Европы примерно на 30 километров.
1 миллиард лет
Примерно столько времени потребовалось, чтобы наша Земля остыла после своего образования. Чтобы на ней появились океаны, зародилась одноклеточная жизнь и вместо атмосферы богатой углекислым газом установилась бы атмосфера, богатая кислородом. За это время Солнце четыре раза прошло по своей орбите вокруг центра Галактики.
Поскольку вселенная всего существует 12-14 миллиардов лет, единицы измерения времени, превышающие миллиард лет, используются достаточно редко. Однако ученые, специалисты по космологии, считают, что вселенная, возможно, будет продолжаться и после того, как погаснет последняя звезда (через сто триллионов лет) и испарится последняя черная дыра (через 10100 лет). Так что Вселенной предстоит еще пройти путь гораздо более длительный, чем она уже прошла.
——————
Хочу обратить ваше внимание на то, что сегодня в ПРЯМОМ ЭФИРЕ будет интересный разговор посвященный Октябрьской Революции. Вы сможете задать вопросы через чат Андрею Фефелову:
Отрицательная степень
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
Например, a n — степень, где:
Читается такое выражение как a в степени n.
Если говорить проще, то степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Свойства степеней
Степень с натуральным показателем в математике имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
Свойство 4: степень произведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень сначала делимое, потом делитель, и первый результат разделить на второй.
Степень с показателем 0
Любое целое a ≠ 0 в степени 0 равно 1.
Выражение 0 в степени 0 многие математики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0; 0).
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с одинаковыми основаниями, но разными показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются, так же как и при умножении положительных степеней:
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:


 masterok
masterok