что значит синус и косинус на обручальных кольцах

Основное тригонометрическое тождество

9 класс, 10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Связь между sin и cos одного угла

Вы уже наверняка знаете, что тождественный — это равный.

Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.

Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:

sin 2 α + cos 2 α = 1

Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.

Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.

В результате деления получаем:

Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.

sin 2 α + cos 2 α = 1

Сумма квадратов синуса и косинуса одного угла тождественно равна единице.

Чтобы доказать тождество, обратимся к теме единичной окружности.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.

Докажем тождество sin 2 α + cos 2 α = 1

Образовался прямоугольный треугольник OA₁B.

Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:

Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.

Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.

Тангенс и котангенс через синус и косинус

Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.

Исходя из определений:

Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.

Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.

Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.

применимо для любого угла α, не равного π * z, где z — это любое целое число.

Связь между тангенсом и котангенсом

Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.

Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.

Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.

tg α * ctg α = 1.

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.

Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.

Тангенс и косинус, котангенс и синус

Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.

Эта связь становится очевидна, если взглянуть на тождества:

Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.

Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.

Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.

Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.

Основные тригонометрические тождества

sin 2 α + cos 2 α = 1

tg 2 α + 1 =

1 + ctg 2 α =

Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.

Примеры решения задач

Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.

Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.

Задачка 2. Найдите значение cos α,
если:

Подставляем значения sin α:

Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.

Источник

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

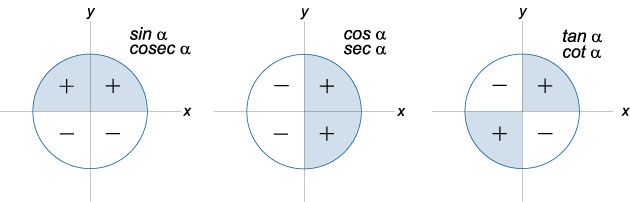
Принцип повтора знаков тригонометрических функций

Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.

В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.

Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.

Тригонометрический круг

Углы в радианах

Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.

Источник

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Угол поворота

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Синус (sin) угла поворота

При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Основные функции тригонометрии

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Источник

Ещё немного о тригонометрии в вычислениях

На Хабре было уже много статей, посвящённых быстрым вычислениям тригонометрии, когда сильно надо, но я хотел бы дополнить их одной небольшой заметкой с отсылкой к школьной тригонометрии.

Иногда может не быть аппаратной реализации тригонометрии, иногда могут быть иные причины, чтобы изобретать методы ускорения вычисления.

Математика

Давайте вспомним некоторые простые формулы из школьного курса.

Начнём с простых:
(1)

Косинус/синус любого угла может быть приведён к аргументу в диапазоне от 0° до 45°, используя формулы первой группы.

Для малых углов тригонометрические функции могут быть сведены к асимптотическим разложениям, если отбрасываемые члены заведомо выходят за разрядную сетку.

Все промежуточные углы могут быть получены суммированием больших углов с некоторым шагом (а для них тригонометрию можно считать таблично), и остатков, которые рано или поздно дадут линейное разложение.

Применение

Дальше нужно будет выбрать шаг таблиц исходя из того, как мы хотим распределить вычисления, показатель степени 11 мы разделим на несколько частей. Например, можно разбить его на две части: 11=6+5, тогда нам понадобятся две таблицы размером 64 и 32 записи (итого 96), или на три части: 11=4+4+3 (размер таблиц 16+16+8=40 записей), но будет больше операций умножения — конкретный выбор будет зависеть от задачи и располагаемых ресурсов.

Ремарка: запись в таблице — это пара синус и косинус аргумента. Если храним с одинарной точностью, то размер записи 8 байт.

Пример

Давайте для примера возьмём разложение 4+4+3, а потом обобщим.

Шаг 1. Приведём аргумент x к нашей шкале, поделив его на константу pi/4 (назовём его x’ ).

[предположим для примера, что получился синус]

Шаг 3. Воспользуемся таблицами (напомню, что их 3), при этом индексами в таблице будут «битовые поля» в двоичном представлении аргумента x» — первые 4 бита после запятой, потом ещё 4, и ещё 3, а оставшиеся не при делах биты пойдут в остаток.

Табличные синус назовём S1, S2, S3, табличные косинусы — C1, C2, C3.

Шаг 4. Объединяем всё, что получилось:

Шаг 5. Если на шаге 2 мы сочли, что результат должен получиться отрицательным, то этот минус надо ввести в результат.

Заключение

Аналогичный подход может использоваться как для вычисления в вещественных числах любого размера, так и, например, для реализации специализированной арифметики с фиксированной запятой. Собственно, в своё время именно последняя задача меня и сподвигла поковыряться в эту сторону, но это было давно.

Источник

Избегаем тригонометрии

Мне кажется, что нам надо использовать меньше тригонометрии в компьютерной графике. Хорошее понимание проекций, отражений и векторных операций (как в истинном значении скалярного (dot) и векторного (cross) произведений векторов) обычно приходит с растущим чувством беспокойства при использовании тригонометрии. Точнее, я считаю, что тригонометрия хороша для ввода данных в алгоритм (для понятия углов это интуитивно понятный способ измерения ориентации), я чувствую, что что-то не так, когда вижу тригонометрию, находящуюся в глубинах какого-нибудь алгоритма 3D-рендеринга. На самом деле, я думаю, что где-то умирает котенок, когда туда закрадывается тригонометрия. И я не так беспокоюсь о скорости или точности, но с концептуальной элегантностью я считаю… Сейчас объясню.

В других местах я уже обсуждал, что скалярные и векторные произведения векторов содержат в себе всю необходимую информацию для поворотов, для тех двух «прямоугольных» операций — синусов и косинусов углов. Эта информация эквивалентна синусам и косинусам в таком большом количестве мест, что кажется, что можно просто использовать произведения векторов и избавиться от тригонометрии и углов. На практике, вы можете это сделать оставаясь в обычных евклидовых векторах, совсем без тригонометрии. Это заставляет задуматься: «А не делаем ли мы чего-нибудь лишнего?» Кажется, делаем. Однако, к несчастью, даже опытные профессионалы склонны к злоупотреблению тригонометрией и делают вещи очень сложными, громоздкими и не самыми лаконичными. И даже возможно «неправильные».

Давайте перестанем делать статью еще более абстрактной. Представим один из случаев замены тригонометрических формул векторными произведениями и увидим о чем я сейчас говорил.

Неправильный вариант поворота пространства или объекта

Пусть у нас будет функция, считающая матрицу поворота вектора вокруг нормализованного вектора на угол . В любом 3D-движке или математической библиотеке реального времени будет одна такая функция, которая скорее всего слепо скопирована с другого движка, википедии или туториала по OpenGL… (да, к этому моменту вы должны признать, и в зависимости от вашего настроения, возможно переживать из-за этого).

Функция будет выглядеть примерно так:

Также, вы знаете, что иногда acosf() может вернуть странные значения, если скалярное произведение выходит за диапазон [-1; 1], и вы решаете изменить его значение так, чтобы оно попало в этот диапазон (прим. пер. to clamp) (в этот момент вы можете даже осмелиться винить точность вашего компьютера, потому что длина нормализованного вектора не равна в точности 1). К этому моменту погиб один котенок. Но пока вы не знаете об этом, вы продолжаете писать свой код. Далее вы вычисляете ось поворота, и вы знаете, что это — векторное произведение вектора вашего объекта и выбранного направления , все точки в вашем объекте будут вращаться в плоскостях, параллельных той, которая определяется этими двумя векторами, так, на всякий случай… (котенка возродили и снова убили). В итоге, код выглядит как-то так:

Чтобы понять, почему это работает, но все еще ошибочно, раскроем весь код rotationAxisAngle() и посмотрим, что же действительно происходит:

Вы можете поспорить, что упрощение нельзя сделать, так как вам нужен будет угол для вычисления синуса. Однако, это не так. Если вы знакомы с векторным произведением векторов, то вы знаете, что так же как скалярное произведение содержит косинус, векторное — содержит синус. Большинство графических программистов понимают зачем нужно скалярное произведение векторов, но не все понимают, зачем нужно векторное произведение (и используют его только для того, чтобы считать нормали и оси поворота). В основном, математический принцип, помогающий нам избавиться от пары cos/acos, также говорит нам о том, что там, где есть скалярное произведение, там возможно векторное произведение, сообщающее отсутствующую часть информации (перпендикулярную часть, синус).

Правильный вариант поворота пространства или объекта

Теперь мы можем извлечь синус угла между и просто посмотрев на длину их векторного произведения… — помним, что и нормализованы! А это значит, что мы можем (мы должны!!) переписать функцию таким образом:

Есть еще одна вещь, которую можно сделать, чтобы избавиться от нормализаций и квадратных корней — инкапсулируя всю логику в одну новую функцию и передавая 1/si в матрицу:

Мы не только избавились от трех тригонометрических функций и избавились от уродливого clamp’а (и нормализации!), но и концептуально упростили нашу 3D математику. Никаких трансцендентных функций, здесь используются только векторы. Векторы создают матрицы, изменяющие другие векторы. И это важно, потому что чем меньше тригонометрии в вашем 3D-движке, тем не только быстрее и яснее он становится, но, прежде всего, математически более элегантнее (правильнее!).

Источник