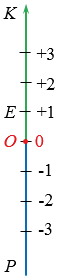что значит точка перед числом
Положительные и отрицательные числа. Координаты на прямой
Определение:
Число 0 не является ни положительным числом, ни отрицательным числом. Оно отделяет положительные и отрицательные числа друг от друга. Все положительные числа и ноль называют неотрицательными числами, а все отрицательные числа и ноль, называют неположительными числами.
Прямые могут находится в различных положениях, поэтому дополнительные лучи могут идти не только влево и вправо, но и в других направлениях. Самые распространенные направления дополнительных лучей: влево и вправо, когда прямая расположена горизонтально (рисунок выше), вверх и вниз, когда прямая расположена вертикально (рисунок ниже).
Определение:
Определение:
Определение:
Обратите внимание, разные координатные прямые могут иметь разные единичные отрезки, так, на рисунке ниже, координатная прямая АВ имеет единичный отрезок, равный 1 клетке, прямая РК имеет единичный отрезок, равный 2 клетки, а прямая МN имеет единичный отрезок, равный 3 клетки.
Изменение величин
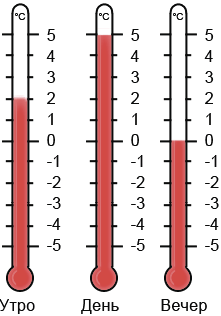
Примером изменения величины может служит изменение температуры в течение дня. Рассмотрим как изменялись показания термометров в течение дня:
Поделись с друзьями в социальных сетях:
Равенство и неравенство. Знаки: больше, меньше, равно
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:
Типы неравенств
Урок 27 Бесплатно Координаты на прямой
В этом уроке мы познакомимся с положительными и отрицательными числами, поймем, к чему относится нуль.
Не забудем рассказать также про неположительные и неотрицательные числа, а после этого узнаем, что такое координатная прямая и из чего она состоит.
Положительные и отрицательные числа
Начнем с сухих, но емких определений.
Обычно + не пишется, а просто подразумевается.
Мы могли бы их записать и со знаком «+»:
В таком случае нужно читать запись буквально: «плюс два», «плюс одна вторая» и так далее.
Такая запись добавляет громоздкости записи, и обычно все- таки «+» опускают.
Приведем примеры отрицательных чисел:
-3, \(\mathbf<-\frac<1><6>>\), \(\mathbf<-32\frac<4><5>>\), -784285332
Читать в данном случае также нужно дословно: «минус три», «минус одна шестая» и так далее.
Минус уже опустить нельзя, так как тогда получится, что число положительное.
Важные факты:
Если нам надо сравнить два числа, одно из которых положительное, а другое отрицательное, то можно смело утверждать, что число, которое положительно, больше числа, которое отрицательно.
Если надо сравнить число с нулем, то достаточно понять, положительное оно или отрицательное. Если положительное, значит, больше нуля, если же отрицательное, то меньше нуля.
Более подробно про сравнение чисел мы поговорим в следующих уроках, а пока потренируемся отличать положительные и отрицательные числа.
Пройти тест и получить оценку можно после входа или регистрации
Неположительные и неотрицательные числа
Иногда необходимо обозначить множество чисел, больших или равных нулю, или же наоборот, меньших или равных нулю.
Удобно, что для этого есть специальные определения.
Соответственно, если мы хотим привести примеры неотрицательных чисел, то можем привести положительные числа или 0.
Примеры: 0, 1, 956, \(\mathbf<\frac<4><9>>\), \(\mathbf<342\frac<1><9>>\).
В данном случае примерами будут соответственно отрицательные числа или 0.
Если необходимо определить, является ли число неотрицательным или неположительным, то ответить надо следующим образом:
Также отметим важные факты про сравнение неположительных и неотрицательных чисел с нулем:
Пройти тест и получить оценку можно после входа или регистрации
Координатная прямая
Начнем с определения, а потом посмотрим на вариации и примеры координатных прямых в жизни.
Если хотя бы одной из этих трех составляющих нет, то прямая уже не может быть координатной.
Выше мы показали самую простую вариацию координатной прямой.
Но обычно для удобства наносят штрихи по всей длине, чтобы не отмерять единичные отрезки.
Также мы можем подписывать числа не только под точкой начала отсчета и точкой, дающей понимание о длине единичного отрезка, но и под остальными точками тоже.
Если мы не хотим загромождать картинку, то можно отмечать точки с какой-то периодичностью.
Неизменным на всех этих картинках остается наличие трех пунктов из определения:
В жизни координатные прямые, полностью удовлетворяющие нашему определению, могут встречаться довольно редко.
Например, на ртутном термометре подразумевается, что направление совпадает с направлением увеличения чисел на шкале.
На нем же мы видим, что числа стоят не у каждого штриха, а у каждого 5-го или каждого 10-го, так картинка становится более читаемой.
Еще один пример: обычная линейка или рулетка. Тут тоже направление подразумевается, поэтому нельзя однозначно сказать, что это координатная прямая.
На линейке, в отличие от градусника, не часто увидишь отрицательные числа. Действительно, -5 градусов интересуют нас больше, чем -5 сантиметров.
На этом рисунке видно, что у точки начала координат (точка O) координата равна нулю, а у точки (А), дающей информацию о единичном отрезке,
координата- 1.
Чтобы найти координату точки мы должны отсчитать количество единичных отрезков между точкой и точкой начало отсчета. А дальше, если эта точка стоит после точки начала отсчета, то взять количество единичных отрезков. В противном случае, если точка находится перед точкой начала отсчета, то взять количество единичных отрезков со знаком «минус».
Например, чтобы найти координату точки C мы отсчитываем количество отрезков от начала координат; получаем, что их 2, запоминаем это.
Точка С находится справа от точки начала отсчета, или дальше по направлению, чем точка начала отсчета. Значит, берем непосредственно число 2 в качестве координаты.
Между точкой B и точкой начала отсчета 3 единичных отрезка, но если смотреть относительно точки начала отсчета, то она находится левее или раньше по направлению, значит, мы берем количество единичных отрезков со знаком «минус» и координатой точки B будет \(\mathbf<-3>\).
Естественно, единичных отрезков между точкой и точкой начала отрезков может получиться нецелое число.
Точка D идет перед точкой начала отсчета, если смотреть по направлению, а значит, координата должна быть отрицательный.
Таким образом, координата точки D будет равна \(\mathbf<-1.5>\).
Мы не случайно отходим от простых понятий «справа»/«слева», когда говорим о взаимном расположении точек.
Представьте, что направление идет в другую сторону.
Ну и конечно же, прямая может быть вообще расположена вертикально, тогда говорить о направлениях «право»/«лево» вообще не приходится.
Пройти тест и получить оценку можно после входа или регистрации
Со знаками «Больше» и «меньше» дети знакомятся еще в детском саду, но в какую сторону они пишутся часто путают.
Разберем способы запоминания математических символов сравнения «>» (знак больше), «» (знак меньше), «=» (равно).

Способ пальцев в определении знаков «больше-меньше»
Он отлично работает в ходе беседы с детьми «правшами», которых в классе большинство.
— Положите кисти рук перед собой на парту.
— Вы много делаете правой рукой?
— Раскройте большой и указательный пальцы правой руки, так чтобы получился уголок. Это знак «больше».
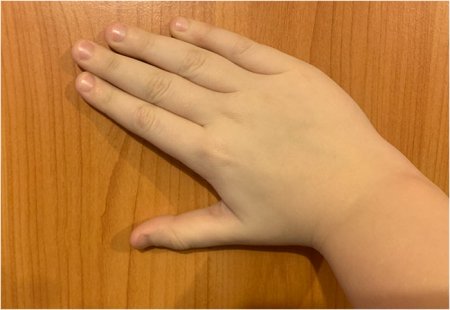
Можно нарисовать на первоначальном этапе на руках буквы «Б» (больше) и «М» (меньше).


Способы: как поставить знак больше, меньше и равно на клавиатуре ≤ и ≥
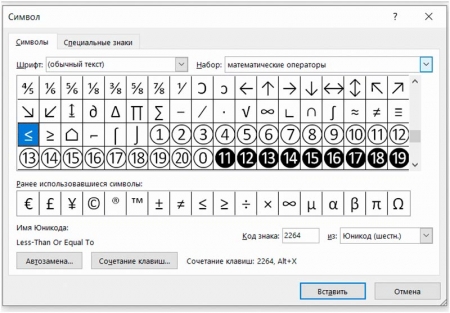
В открывшемся окне отображается все возможные символы которые можно вставить, но их там довольно много (не одна сотня штук). Для быстрого поиска символов «больше или равно» и «меньше или равно» в выпадающем меню справа «Набор» выбираем пункт «Математические операторы». Выделяем символ нужный символ (например, как на картинке ≤, «меньше или равно») и нажимаем кнопку «Вставить».
А теперь потренируйтесь в постановке знаков «больше», «меньше», «равно». Если вы знаете какой-то способ запоминания, то напишите в комментариях. Давайте делиться полезными идеями!
Математика
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
В выходной день папа с Никитой собирались в городской парк, на открытие большой горки.
А если, говоря о погоде, используется слово «плюс», или сообщается количество градусов с использованием выражения «выше нуля», например: «сегодня за окном пятнадцать градусов выше нуля», или «на улице плюс три», то значит, что шкала термометра поднялась выше 0.
Но даже после папиного рассказа у Никиты осталось много вопросов о числовых значениях со знаком минус и плюс. Всю прогулку мальчик думал о непонятных цифрах со знаком «минус».
Найти ответы на все свои вопросы Никита смог, только после того, как внимательно изучил наш урок на сайте 100urokov.ru.
Положительные числа
В каждом доме и квартире есть термометр– незаменимый прибор для измерения температуры воздуха. Давайте внимательно его рассмотрим.
Мы видим шкалу, с нанесенными цифрами, которая расположена в стеклянной колбе. Стоит отметить, что шкала прибора разделена точно пополам делением с цифрой 0. Все цифры, находящиеся вверху от нуля имеют положительное значение и записываются со знаком «плюс».
В арифметике такие значения имеют свое название – положительные.
Примеры положительных чисел: 5,18,39,156.
Исходя из рассмотренного правила, делаем вывод, что числа, перед которыми не стоит знак и числа со знаком «+» равны.
Положительные числа можно использовать для выполнения любых математических действий:
возведения в степень.
Получается, что именно с положительными значениями вы знакомы с первого класса.
Отрицательные числа
Ну а теперь, давайте представим, что за окном зима. Какую же температуру покажет рассмотренный прибор для измерения температуры воздуха?
В зимнее время года холодно. Поэтому, обычно говорят, что держится минусовая температура, то есть столбик прибора не поднимается выше 0.
В математике такие числа принято называть отрицательными, при записи, перед данным числовым значением нужно ставить знак «минус».
Примеры отрицательных чисел:
Координатная прямая
Давайте внимательно рассмотрим шкалу термометра и постараемся схематично её изобразить. Шкала является прямой линией. Чертим её:
Замечаем, что каждое деление соответствует 1 градусу. Выходит, шкала имеет единичный отрезок.
Выбираем на нашем рисунке единичный отрезок не забывая, отложить его в обе стороны от начала отсчета:
Посмотрим на полученное изображение. Построенная геометрическая фигура имеет направление, точку начала отсчета и единичный отрезок. В математике, такие фигуры имеют свое название – координатная прямая.
Важным моментом, является то, что на координатной прямой по правую сторону от точки начала отсчета (0) находятся положительные числа, а по левой стороне – отрицательные (записанные со знаком «минус»).
На самом деле, на рисунке изображен небольшой фрагмент прямой. Данная линия продолжается в обе стороны до бесконечности, так как по определению, она не имеет ни начала, ни конца.
Координата точки
Каждая точка, нанесенная на координатную прямую,всегда имеет свое числовое обозначение или координату.
Разберем на примере.
Построим координатную прямую. Нанесем начало отсчета и выберем единичный отрезок, равный 1 сантиметру. Обозначим деление буквой A:
Читается, точка A с координатой 1.
Нет ничего сложного!
Давайте применим на практике полученные знания и разберем задание.
Постройте координатную прямую и нанесите на неё точки:В(4), С(-2).
Чтобы выполнить данное задание необходимо изобразить прямую, выбрать на ней направление, точку начала координат и единичный отрезок, который будет равен 1 сантиметру.
Теперь нужно поставить точку В с координатой 4. Значение координаты точки положительное, поэтому отмечать её, будем с правой стороны от начала отсчета (0).Координата 4 говорит о том, что отметка В находится от нуля на расстоянии четырех единичных отрезков, то есть, расстояние от нуля до отметки В равно четырем сантиметрам.
Запомни! Положительные числа всегда расположены с правой стороны от нуля, а отрицательные числа с левой стороны от точки начала координат. В данном случае ноль и есть точка начала координат.
Противоположные числа
Рассмотрим такую ситуацию.
На уроке, учительница математики, Нина Николаевна вызвала Егора к доске и дала задание, построить координатную прямую и нанести на неё две отметки с различными координатами положительной и отрицательной.
Егор выполнил задание. Мальчик построил координатную прямую, отметил точку начала координат, направление и единичный отрезок. После этого, школьник нанес на прямую отметки M(3) и K(-3).
Но Егор с нетерпением ждал пояснений Нины Николаевны.
Учительница объяснила детям, что в математике, числа, которые отличаются только знаком, имеют собственное название – противоположные числа.
Если два числа отличаются только знаком, то их называют противоположными числами.
Примеры противоположных чисел:
Но при этом, модули противоположных чисел всегда равны.
Мы видим, что от начала отсчета до точек с координатами (4) и (-4) отложено равное количество единичных отрезков – четыре. Поэтому модуль (количество единичных отрезков от нуля до выбранной точки) в рассматриваемых записях будет одинаковым – |4|.
Выходит, что у противоположных числовых значений равными будут только модули! А сами числа имеют совершенно разное числовое значение!
Егор получил заслуженную пятерку за правильно выполненное задание.
Минутка истории
Отрицательные числа стали для нас чем-то обычным и привычным. Но так было не всегда. Довольно длительное время, положительные значения определяли словом «прибыль», а отрицательные трактовали, как «убыток». И другого применения отрицательным числам не было.
Первыми, признали отрицательные числа, правители Китая в начале 3 века, до нашей эры. Но, несмотря на это, большая часть китайцев считала данное решение правительства бессмысленным. Так как использовать на практике отрицательные числа было негде.
После, числовые значения со знаком «минус», стали использовать в Индии. Их применяли для записи долгов.
В Европу, значения со знаком «минус», попали благодаря Леонардо Пизанскому. Леонардо начал использовать отрицательные числа исключительно для записи в долговой книге и проведения финансовых операций, связанных с долгами. А уже в 1202 году Пизанский подсчитывал свои убытки пользуясь числовыми значениями со знаком «минус».
Однако до начала 19 века рассматриваемые значения находились в гонениях мировых математиков. Ученые утверждали, что выражение 0-4=0 бессмысленно, так как не существует числового значения, которое меньше чем «ничто» (нуль). Поэтому великие математики старались не использовать «бесполезные» цифры в своих вычислительных операциях.