что значит значение функции в точке
Как решать задачи на функцию
Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».
После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание. Функция задана формулой « y = 2x − 1 »
Для того, чтобы вычислить « y » при « x = 15 » достаточно подставить в функцию вместо « x » необходимое числовое значение.
Запись решения выглядит следующим образом.
Для того, чтобы найти « x » по известному « y », необходимо подставить вместо « y » в формулу функции числовое значение.
Мы получили линейное уравнение с неизвестным « x », которое решается по правилам решения линейных уравнений.
Не забывайте про правило переноса в уравнениях.
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на « −1 » для смены знака.
Как проверить верно ли равенство для функции
Рассмотрим задание. Функция задана формулой « f(x) = 2 − 5x ».
Верно ли равенство « f(−2) = −18 »?
Чтобы проверить верно ли равенство, нужно подставить в функцию « f(x) = 2 − 5x » числовое значение « x = −2 » и сопоставить с тем, что получится при расчетах.
Когда подставляете отрицательное число вместо « x », обязательно заключайте его в скобки.
Не забывайте использовать правило знаков.
Неправильно
Правильно
С помощью расчетов мы получили « f(−2) = 12 ».
Это означает, что « f(−2) = −18 » для функции « f(x) = 2 − 5x » не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию « y = x 2 −5x + 6 »
Для этой задачи нет необходимости, строить график заданной функции.
Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси « Ox » вместо « x » и координату по оси « Oy » вместо « y »).
Вместо « x » подставим « 1 ». Вместо « y » подставим « 2 ».
У нас получилось верное равенство, значит, точка с координатами (1; 2) принадлежит заданной функции.
Вместо « x » подставим « 0 ». Вместо « y » подставим « 1 ».
В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции « y = x 2 − 5x + 6 »
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.
Рассмотрим функцию « y(x) = −2x + 1 ». Её график мы уже строили в предыдущем уроке.
Для этого из значения « 2 » на оси « Ox » проведем перпендикуляр к графику функции. Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси « Oy ».
Полученное значение « −3 » на оси « Oy » и будет искомым значением « y ».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции « y(x) = −2x + 1 ».
Значит, мы правильно получили координаты с графика функции.
Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений « x » в функцию.
При подстановке числового значения « x » в функцию в результате должно получиться то же значение « y », которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Возрастание и убывание функции на интервале, экстремумы
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Точки экстремума, экстремумы функции
Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.
Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Иначе говоря, получим их условия постановки знака:
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
После чего необходимо найти производную:
Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
Изображение на прямой имеет вид
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
Перейдем к вычислению минимумов:
Произведем вычисления максимумов функции. Получим, что
Второй признак экстремума функции
Для начала находим область определения. Получаем, что
Необходимо продифференцировать функцию, после чего получим
Третье достаточное условие экстремума
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.
Непрерывность функции в точке, разрывы первого и второго рода
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
Решение
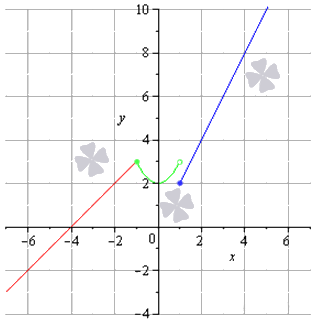
Соответствующая последовательность значений функций выглядит так:
на чертеже они обозначены зеленым цветом.
Соответствующая последовательность функций:
на рисунке обозначена синим цветом.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
Устранимый разрыв первого рода
Решение
Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Решение
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
Ответ: в конечном счете мы получили:
Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Решение
Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:
Ей соответствует последовательность значений функции:
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Производная
Производная – отношение приращения функции к приращению ее аргумента при приращении аргумента стремящемся.
ЭЙ-ЭЙ, СТОЙТЕ. Куда вы побежали-то? Сейчас легко и просто всё объясню! Приготовьтесь, текста будет много. Зато понятно и наглядно. Так же в конце будут разобраны примеры из ЕГЭ.
Понятие производной на интервале
Значению аргумента \(x_B\) соответствует точка \(B\) на графике и значение функции \(y_B\).
Давайте обозначим «расстояние» между \(y_B\) и \(y_A\) как некоторое \(∆y\) (аналогично тому, как это было сделано на оси \(x\)).
Что такое \(∆y\)? Подумайте – был аргумент равный \(x_A\), ему соответствовало значение функции \(y_A\). Потом мы аргумент увеличили на \(∆x\) (до \(x_B\)), при этом значение функции тоже выросло до \(y_B\). Что такое тогда \(∆y\) равное разности между \(y_B\) и \(y_A\)? Верно, это приращение значения функции при соответствующем приращении аргумента!
Внимание! Это определение не математически строгое, а «по смыслу», для понимания.
То есть, производная на интервале показывает насколько сильно изменилась функция по отношению к некоторому изменению аргумента этой функции. Или по-другому: производная на интервале характеризует скорость роста функции на этом интервале.
Действительно, посмотрите два графика ниже.
На первом графике при росте аргумента с \(3\) до \(4\), функция выросла с \(1\) до \(4\). Значит:
\(∆x=x_B-x_A=4-3=1\),
\(∆y=y_B-y_A=4-1=3\),
т.е. значение производной на интервале \((3;4)\) равно \(\frac<∆y><∆x>=\frac<3><1>=3\)
На втором графике при росте аргумента с \(3\) до \(4\), функция выросла с \(2\) до \(3\). Значит:
\(∆x=x_B-x_A=4-3=1\),
\(∆y=y_B-y_A=4-1=3\),
т.е. значение производной на интервале \((3;4)\) равно \(\frac<∆y><∆x>=\frac<1><1>=1.\)
Легко заметить, что график слева «круче», а график справа – более «пологий», т.е. \(f(x)\) растет быстрее, чем \(g(x)\). И производная слева – больше, чем справа. Это логично, ведь фактически производная – это дробь \(\frac<∆y><∆x>\), а если числитель дроби увеличить, то и значение всей дроби тоже растет.
Производная на интервале характеризует скорость роста функции. Чем больше производная – тем быстрее растет функция на интервале.
Хорошо, теперь вопрос на засыпку тем, кто читал внимательно. А что будет с производной, если график линейной функции падает?
Давайте рассмотрим эту ситуацию.
Функция \(f(x)\) падает, то есть при росте аргумента, значение функции становиться все меньше.
Действительно, при росте аргумента с \(2\) до \(3\), функция упала с \(4\) до \(1\). Значит, \(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-4=-3\).
Тогда значение производной на интервале \((3;4)\) равно \(\frac<∆y><∆x>=\frac<-3><1>=-3\).
На первом графике при росте аргумента с \(2\) до \(3\), функция упала с \(4\) до \(1\). Значит:
\(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-4=-3\),
т.е. значение производной на интервале \((2;3)\) равно \(\frac<∆y><∆x>=\frac<-3><1>=-3\).
На втором графике при росте аргумента с \(2\) до \(3\), функция упала с \(2\) до \(1\). Значит:
\(∆x=x_B-x_A=3-2=1\),
\(∆y=y_B-y_A=1-2=-1\),
т.е. значение производной на интервале \((2;3)\) равно \(\frac<∆y><∆x>=\frac<-1><1>=-1\).
Если функция падает – производная на интервале отрицательна.
Вот, например, функция, имеющая прямолинейный участок, параллельный оси \(x\) на интервале \((2;4)\). Понятно, что если мы рассмотрим этот интервал, то изменение функции \(∆y\) на нем равно нулю, ведь на нем функция не растет и не падает и для любой точки равна \(2\).
И тогда производная равна \(\frac<∆y><∆x>=\frac<0><∆x>=0\).
Если функция не растет и не падает – производная на интервале равна \(0\).
Понятие производной в точке
Хорошо, мы разобрали производную на интервале для линейной функции. А если функция отличается от прямой?
Если мы рассмотрим интервал по иксу с \(2\) до \(4\), то на нем прирост значения функции – с \(1\) до \(3\). То есть, \(∆x=4-2=2\), \(∆y=3-1=2\), т.е. значение производной на интервале \((2;4)\) равно \(\frac<∆y><∆x>=\frac<2><2>=1\).
Если мы рассмотрим интервал по иксу с \(2\) до \(3\), то на нем прирост значения функции – с \(1\) до \(2\). То есть, \(∆x=3-2=1\), \(∆y=2-1=1\), т.е. значение производной на интервале \((2;3)\) равно \(\frac<∆y><∆x>=\frac<1><1>=1\).
Теперь давайте посмотрим график некоторой нелинейной функции.
Если мы рассмотрим интервал по иксу с \(2\) до \(5\), то на нем прирост значения функции – с \(1\) до \(4\). То есть, \(∆x=5-2=3\), \(∆y=4-1=3\), т.е. значение производной на интервале \((2;5)\) равно \(\frac<∆y><∆x>=\frac<3><3>=1\).
Если же мы рассмотрим интервал по иксу с \(2\) до \(4\), то на нем прирост значения функции – с \(1\) до \(2\). То есть, \(∆x=4-2=2\), \(∆y=2-1=1\), т.е. значение производной на интервале \((2;4)\) равно \(\frac<∆y><∆x>=\frac<1><2>=0,5\).
Получается, что значение производной изменяется в зависимости от ширины рассматриваемого интервала. Чтобы выйти из этой ситуации и при этом сохранить все вышеописанную логику, математики придумали следующую хитрость.
Дело в том, что при увеличении масштаба график любой нелинейной функции становится все больше похож на линейный.
Вот, например, график параболы \(y=x^2\), построенный на компьютере с высокой точностью, на интервале от \(-5\) до \(5\). Видно, что график ну очень далек от прямой.
А если рассмотреть тот же график, но на более узком интервале?
Вот тот же график, но уже на интервале от \(0\) до \(2\). Видно, что он изрядно «распрямился».
А вот он же на интервале от \(1\) до \(1,1\). Визуально он уже мало отличается от прямой, хотя на самом деле очень небольшое искривление все же есть. Понятно, что если сжимать интервал еще сильнее, то вскоре график будет практически неотличим от прямой.
Таким образом, вся вышеописанная логика вполне применима и для нелинейных графиков, но только на очень маленьких интервалах. А что мы получим, если будем БЕСКОНЕЧНО уменьшать ширину интервал? Мы будем сжимать его до точки. А что такое «ширина интервала»? Это ни что иное как \(∆x\)! Значит, чтобы найти производную в точке, мы должны посмотреть приращение функции на бесконечно малом (или, говоря более научно, стремящемся к нулю) приращении аргумента. Именно так в математике и вводится понятие производной в точке:
Производная в точке – есть отношение приращения функции к соответствующему приращению ее аргумента при приращении аргумента, стремящемся к нулю.
Остается вопрос – а есть ли на нелинейных функциях точки, где производная равна нулю? Ответ – да, в точках экстремумов. Помните, что это за точки такие?
Экстремумы – это точки максимумов и минимумов функции.
Напомню, что максимумом функции называется самая «высокая» точка на некотором интервале, а минимумом, соответственно, самая «низкая».
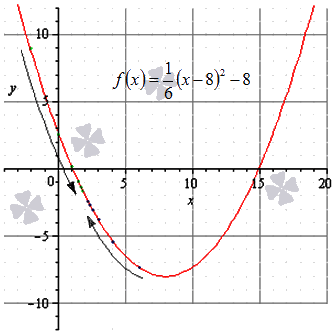
Вот, например, функция \(y=(x-5)^2 (x+1)-15\).Она имеет максимум при \(x=1\) и минимум при \(x=5\).
И в этих точках функция действительно не растет и не падает.
Давайте посмотрим на большем масштабе, чтобы в этом убедится.
Вот окрестность точки максимума \(x=1\) с очень маленьким шагом.
А это окрестность точки минимума \(x=5\) с очень маленьким шагом.
Думаю, комментарии излишни. Вообще говоря, чтобы понять, что в максимумах и минимумах функция «останавливается» достаточно просто внимательно об этом подумать.
Таким образом, получается, что в окрестности точек минимума и максимума функция идет параллельно оси \(x\). И в них производная равна нулю. Слово «в окрестности», употребленное выше, означает «очень-очень близко возле точки». Например, промежуток \((1,99999; 2,00001)\) можно назвать окрестностью точки со значением \(2\).
— Чем больше значение производной функции в точке – тем быстрее в этой точке растет функция.
— Если производная в точке положительна, функция в этой точке растет, если производная в точке отрицательна, функция в ней падает.
— В точках максимумов и минимумов функции – производная равно \(0\).
Эти принципы стоит запомнить (а еще лучше просто понять), потому что с их помощью можно решать огромное количество задач на производные, в том числе и из ЕГЭ.
Пример (ЕГЭ). На рисунке изображен график функции, определенной на интервале \((-3;7)\). Определите количество целых точек, в которых производная данной функции отрицательна.
Решение: Начинаем анализировать. Где производная будет отрицательна? Там, где функция падает, то есть от точки А до точки В и от точки С до точки D.
При этом в задаче просят найти количество ЦЕЛЫХ точек. А что такое «целая точка»? Это такая точка графика, у которой икс целое число (например, \(-5\), \(0\) или \(17\), но не \(3,25\) или \(0,7\)).
То есть нам нужны именно такие точки на участках АВ и CD графика. Всего их четыре (обозначены на графике красным ромбом). Обратите внимание, что точка С в ответ не входит, так как это точка максимума и в ней производная равно \(0\), а ноль неотрицателен.
Пример (ЕГЭ). На рисунке изображен график функции \(y=f(x)\) и отмечены точки \(−2\), \(1\), \(3\) и \(9\). В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Решение: Давайте думать.
В точке с координатой \(-2\) функция убывает (падает), значит производная будет отрицательна (ведь она показывает, как раз изменение функции).
В точке с координатой \(1\) – функция медленно растет, значит производная будет, во-первых, положительна, а во-вторых, мала по значению (ведь рост медленный).
В точке с координатой \(3\) – максимум, значит функция не растет и не падает, следовательно, производная будет равна нулю.
И наконец, в точке \(9\) – функция растет и быстро (по крайней мере, быстрее, чем в точке \(1\)). Значит здесь производная положительна и велика.
Таким образом, с учетом всех предыдущих рассуждений, делаем вывод: наибольшее значение производной будет в точке \(9\).
Довольно часто в практике попадаются обратные задачи – когда дан график производной, а анализировать надо график функции. Вот, например, такая задача из ЕГЭ:
Решение: Экстремумы – это точки минимумов и максимумов функции. Но у нас дан график производной, а не функции. А что происходит с производной в тех точках, где на функции минимум или максимум?
Верно, в этих точках производная равна нулю. Значит, нам нужны все точки, где значение производной ноль! Это точки А, B, C, D и Е. Всего их \(5\), это и есть ответ задачи.
Решение: Мы знаем, что если функция возрастает – производная положительна, а если падает – то отрицательна. Однако верно и обратное:
— если производная положительна – функция растет,
— если производная отрицательна – функция падает.
Исходя из этого становиться очевидно, что исходная функция \(y(x)\) возрастает на участках \((-5;-2)\) и \((1;6)\) – они выделены зеленым. И длина наибольшего из них равна \(5\).