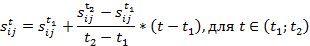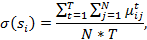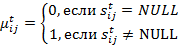Cortona3d viewer что это за программа и нужна ли она
Текущие плагины и программы для Mozilla Firefox ® и др.
Главное меню
Ссылки на ресурсы
Навигация по сайту
Бесплатный мультиязычный проигрыватель Cortona3D Viewer предназначен для интерактивного 3D-просмотра VRML файлов (.WRL).
— для интернет-браузеров: Internet Explorer, Netscape Browser, Mozilla, Firefox и др.
— для офисных приложений: Microsoft PowerPoint, Microsoft Word и т.д.
В данный момент времени проигрыватель Cortona3D Viewer доступен только для платформ Windows.
Программа оптимизирована для качественной 3D визуализации изображения, в том числе и на нескольких мониторах, поддерживает новые технологии визуализации современных видеокарт.
Cortona3D Viewer версий 6.х. (устаревший).
Cortona3D Viewer работает в операционных системах: Windows 2000 (SP4); Windows XP (SP2); Windows Vista (SP1).
Cortona3D Viewer v. 7.0.
Системные требование:
Поддерживаемые веб-браузеры:
Установка Cortona3D Viewer.
Панель управления Cortona3D Viewer.
Для того чтобы пользователь не ломал голову, разработчики создали три основные кнопки управления: «Ходьба«, «Полёт» и «Изучение«.
При нажатой левой кнопкой и перемещением мышки двигаемся и вращаемся, курсор соответственно будет менять вид: стрелка вверх, вниз, поворот и т.д.
на рис. показана панель управления Cortona3D Viewer (вызывается нажатием правой кнопкой мышки по изображению сцены, расположенной на странице)
Как видно из картинки, Cortona3D Viewer имеет русскоязычный интерфейс и множество настроек для регулировки просмотра 3D сцены в интернет-браузере.
Трёхмерные виртуальные интернет-миры (3D сцены).
В интернете множество ресурсов использующих технологию Cortona3D, которые дают возможность окунуться в виртуальный 3D-мир и получить больше качественно-полезной информации.
Размер изображений порядка 3 Мб, поэтому для комфортного путешествия Вам потребуется высокоскоростное широкополосное соединение с интернетом.
Пирамиды Египта.
Сайт на английском и французском языках, что сегодня, имея в составе браузера расширения-трансляторы, не имеет ни какого значения.
Надоело? Ага! Вас интересуют звёздные миры! Пожалуйста, перейдем в планетарий. На странице сайта выбираем соответствующие опции (небесный экватор, эклиптику и т.д., месторасположение, например Москва) и в полёт (сайт на английском, испанском и французском).
Планетарий.
Да. не впечатлило, а слабо по путешествовать во времени и перенестись в далёкую Италию, в город Venzone и прочувствовать атмосферу средневековья? Да легко.
Venzone.
«I HAVE A VRML PLUG-IN AND I WANT TO ENTER VENZONE 3D»
Надоели бродилки, хочется почесать затылок и покрутить чего-нибудь в руках, например кубик Рубика, который пылится на полке с незапамятных времён, но всё непонятно, а хочется иногда блеснуть своими незаурядными способностями, да и это не проблема с технологиями 3D. Достаточно перейти на сайт Zumbo (Италия) и Вы узнаете об этой головоломке всё!
Кубик Рубика.
Мавзолей. (Москва, Красная площадь, для тех кто не был и не видел «живее всех живых».)
Дуэль.
27 января 1837 около 5 вечера Пушкин был смертельно ранен на дуэли с Жоржем Дантесом, приемным сыном голландского посланника в России.
Если заинтригованы, то не только посмотреть, но Вы можете и прослушать озвученные исторические события.
Орбитальная станция «МИР».
Станцию «МИР», за 15 лет её работы, посетило свыше 100 космонавтов и астронавтов. Осуществлено 78 выходов в открытый космос. Мировые рекорды по пребыванию в космосе:
Станция выведена из эксплуатации 23 марта 2001. Несгоревшие в атмосфере останки «Мир» приводнились в районе Тихого океана примерно в 9.00 по московскому времени.
Космический корабль «Восток».
«12 апреля 1961 Юрий Гагарин совершил первый в истории человечества космический полёт, за 1 ч 48 мин он облетел земной шар. «
На данном сайте обязательно включите звук на своём компьютере, чтобы полностью приблизиться к величайшему всемирному историческому событию.
Надеюсь, что эта небольшая подборка даст Вам начальный старт в интереснейший мир 3D! А возможно Вы сами создадите свой мир, ведь у нас в России столько уникальных городов, исторических памятников созданных нашими предками, да вообще мало ли чем в России можно восхищаться, дерзайте.
На странице использован сервис tinyurl, для создания коротких ссылок.
Тема 5. Приложения анализа научных данных методом визуализации
5.1. Введение
Эти работы включают в себя:
5.2. Комплекс инструментальных программных средств анализа научных данных методом визуализации.
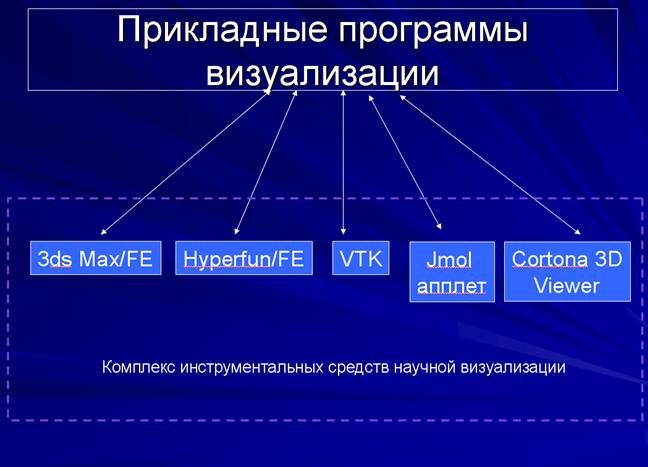
Комплекс представляет собой совокупность автономно и совместно используемых программных продуктов 3ds Max, HyperFun, Jmol апплет,VTK, Cortona3D Viewer и их функциональных расширений (FE)[3]. Взаимодействие прикладных программ и комплекса показано на Рис.5.1.
Рис. 5.1. Взаимодействие прикладных программ и комплекса
Следует отметить, что указанные инструментальные программные средства комплекса научной визуализации обладают широкими функциональными возможностями, которые позволяют создавать на их основе сложные прикладные программы для пассивной и интерактивной визуализации. Охарактеризуем компоненты данного комплекса.
Характеристика программных продуктов 3ds Max, HyperFun и VTK в контексте реализуемых ими функциональных процедур визуализации была приведена в предыдущем разделе “Инструментальные средства научной визуализации”. Рассмотрим характеристики программных продуктов Jmol апплет и Cortona3D Viewer.
Jmol апплет
Jmol апплет обеспечивает возможность моделирования и рендеринга специализированных пространственных сцен [6]. В большинстве случаев геометрическая модель пространственной сцены представляет собой совокупность сфер (атомы) и цилиндров (связи между атомами). Наряду с этим Jmol апплет представляет функциональные возможности для задания ряда физических характеристик пространственной сцены. Наряду с этим, Jmol апплет обеспечивает выполнение функциональных процедур измерения пространственной сцены и выполнения необходимых вычислений.
Необходимо отметить, что апплет обеспечивает возможность написания как пассивных, так и интерактивных прикладных программ визуализации, предназначенных для выполнения на локальном компьютере или в сети Интернет.
Указанные выше функциональные возможности Jmol апплета доступны из прикладной программы визуализации, написанной на языке Jmol Scripting Language.
Cortona 3D Viewer
Программа представляет собой плагин браузера для высококачественного рендеринга статических и динамических пространственных сцен, описание которых представлено в формате VRML [7]. Предоставляются версии работающие с браузерами Internet Explorer, Netscape Browser, Mozilla Firefox, Google Chrome. В настоящее время Cortona3D Viewer работает в среде Windows.
5.3. Прикладные программы визуализации
Прикладные программы визуализации, разработанные на базе инструментальных программных средств комплекса, предназначены для решения различных задач, которые имеют место в рамках проводимых в МИФИ исследований различных наноструктур. Среди этих задач можно выделить две типовые задачи:
Рассмотрим примеры разработанных прикладных программ визуализации анализируемых наноструктур.
Программа визуализации нанообъектов N192
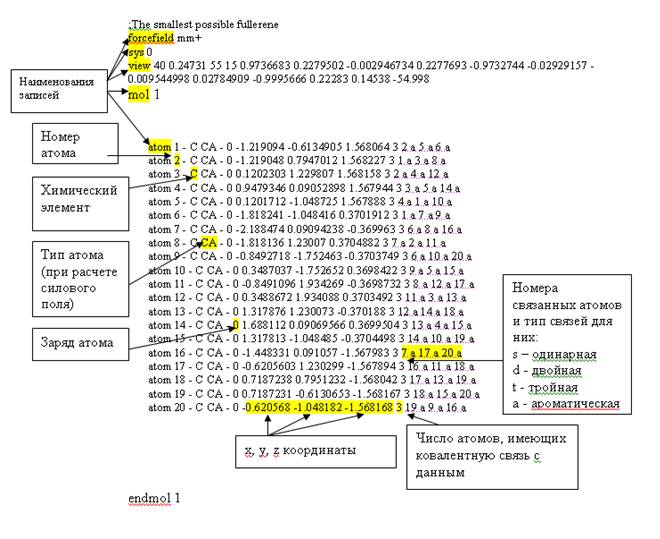
В этой программе визуализации в качестве исходных данных используется описание анализируемого нанообъекта N192 в формате XYZ – файла. Описание структуры формата представлено на Рис.5.2.
Рис.5.2. Структуры формата XYZ-файла
Результатом работы этой программы является интерактивное проекционное графическое изображение нанообъекта. Пример такого изображения показан на Рис.5.3.
Рис.5.3. Интерактивное графическое изображение нанообъекта N192
Программа написана на языке Maxscript, при ее работе используются компоненты комплекса 3ds Max и Cortona3D Viewer. Задаваемыми параметрами пространственной сцены в программе являются длины двойных, тройных и одинарных связей, цвет атомов, цвет связей. Использование компонента Cortona3D Viewer позволяет осуществлять интерактивную визуализацию исходных данных, задавая различные значения штатных атрибутов рендеринга (положение камеры, цвет фона и т.д.). При помощи этой программы решается задача анализа взаимного расположения атомов в исследуемой наноструктуре.
Анимационная программа визуализации формирования нанообъектов из 2-х фуллеренов С20
В качестве исходных данных в этой программе визуализации используется описание анализируемого динамического процесса объединения 2-х фуллеренов С20 в один кластерных димер С40 в формате TXT – файлов. Анимационная структура содержит последовательный набор TXT файлов, где каждый файл содержит описание координат атомов в определенный момент времени, который указан в названии файла. Описание структуры формата для одного TXT файла представлено на Рис.5.4.
Рис.5.4. Структура формата TXT файла
Результатом выполнения этой программы является анимационное проекционное графическое изображение процесса объединения 2-х наноструктур. Пример такого изображения показан на Рис.5.5.
Рис.5.5. Анимационное графическое изображение процесса объединениия 2-х наноструктур С20
Программа написана на языке Maxscript, при ее работе используются компонент комплекса 3ds Max и его функциональное расширение в виде плагина NLink. Задаваемыми параметрами в программе являются штатные атрибуты рендеринга, пороговая длина связей (визуализируются только те связи, длина которых не превосходит значение пороговой длины), цвет сферических и цилиндрических объектов, используемых в пространственной сцене. При помощи этой программы решается задача анализа исследуемого процесса формирования кластерного димера.
Программа визуализации нанообъектов различных типов
Рис.5.6. Структура формата HIN-файла
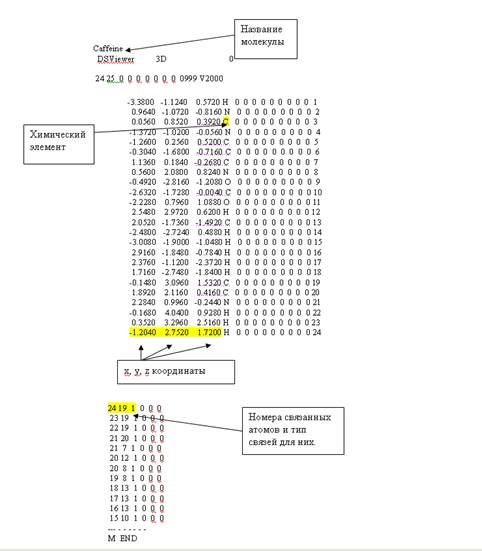
Рис.5.7. Структура формата MOL-файла
Рис.5.8. Структура формата используемого в программе фрагмента OUT-файла
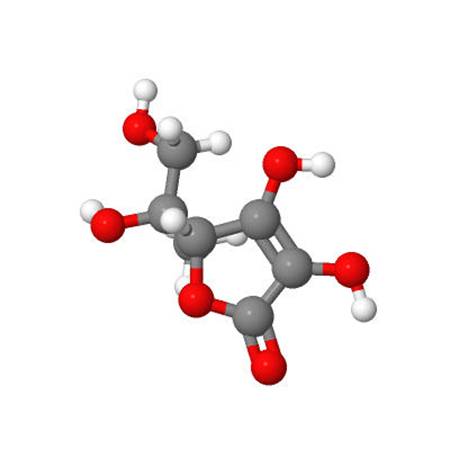
Результатом работы этой программы является статическое проекционное графическое изображение визуализируемого нанообъекта. Примеры таких изображений нанообъектов С180 и Витамин С показаны соответственно на Рис.5.9, 5.10.
Рис.5.9. Графическое изображение наноструктуры фуллерен С180
Рис.5.10. Графическое изображение наноструктуры Витамин С
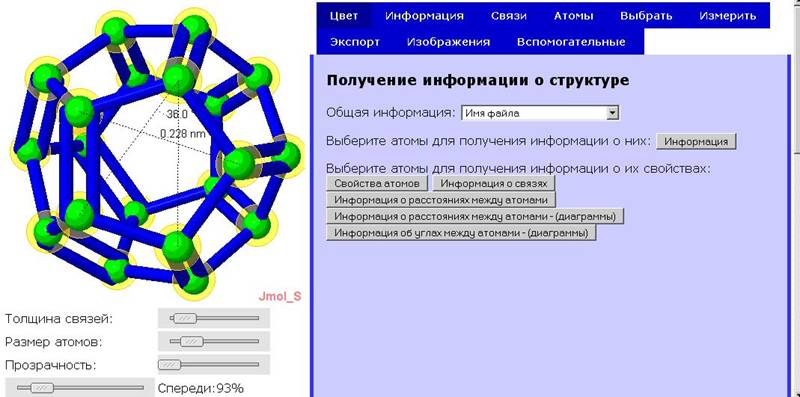
Программа написана на языке Jmol Scripting Language, при ее работе используются компонент комплекса Jmol апплет. Задаваемыми параметрами в программе являются длины двойных, тройных и одинарных связей, цвет сферических и цилиндрических объектов, используемых в пространственной сцене. (Рис.5.11). Программа может осуществлять измерение расстояний между атомами, углов между связями (Рис.5.12), строить гистограммы (Рис.5.13), производить редактирование наноструктуры (Рис.5.14). Использование компонента Jmol апплета позволяет осуществлять интерактивную визуализацию исходных данных, задавая различные значения штатных атрибутов рендеринга – положение камеры, среду и т.д. Различные варианты использования этой программы представлены на Рис.5.11 – 5.14. При помощи этой программы решается задача качественного и количественного анализа взаимного расположения атомов в исследуемой наноструктуре.
 | |
| Рис.5.11. Задание параметров программы | |
 | |
| Рис.5.12 Измерение расcтояний и углов | |
 | |
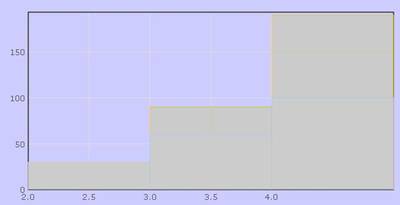 | 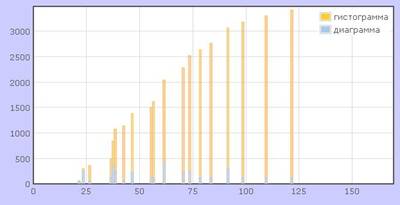 |
| Рис.5.13.Построение гистограмм | |
 | |
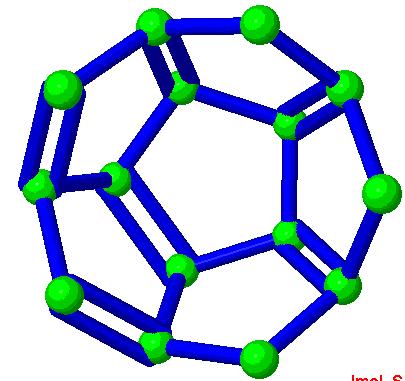 |  |
Рис.5.14. Редактирование наноструктуры
Анимационная программа визуализации изоповерхности для параметра порядка трехмерного сверхпроводника 2-го рода
Рис.5.15. Структура формата TXT- файла
Результатом работы этой программы является анимационное проекционное графическое изображение изоповерхности поля ( поверхность определяет положение и конфигурацию вихрей Абрикосова). Пример такого изображения показан на Рис.5.16.
Рис.5.16. Анимационное графическое изображение изоповерхности поля параметра порядка сверхпроводника 2-го рода
Программа написана на языке Maxscript, при ее работе используются компоненты комплекса 3ds Max и его функциональные расширения плагины MDSpace, FromFile, а также компонент HyperFun и его функциональные расширения OpenFile, CloseFile, ReadSupercond. Задаваемыми параметрами в программе являются выбранное значение поля, штатные атрибуты рендеринга. При помощи этой программы решается задача анализа поля исследуемого сверхпроводника.
Программа визуализации векторного поля для параметра порядка трехмерного сверхпроводника 2-го рода
Рис.5.17. Структура формата TXT- файла
Результатом работы этой программы является инерактивное проекционное графическое изображение линий тока векторного поля ( цветом моделируется модуль вектора). Пример такого изображения показан на Рис.5.18.
Рис.5.18. Графическое изображение линий тока для векторного поля параметра порядка сверхпроводника 2-го рода
Программа написана на языке С++, при ее работе используется компонент комплекса VTK. Задаваемыми параметрами в программе являются расположение начальных точек для линий тока и их количество, а также штатные атрибуты рендеринга. При помощи этой программы решается задача анализа векторного поля исследуемого сверхпроводника.
Наряду с линиями тока, в этой программе для визуализации векторного поля может быть использовано также его «стрелочная» интерпретиция (рис. 5.19).
Рис.5.19. Графическое изображение линий тока для векторного поля, а также «стрелочной» интерпретации самого поля параметра порядка сверхпроводника 2-го рода
Анимационная программа объемной визуализации электронной плотности нанообъектов Cl2O
В этой программе визуализации в качестве исходных данных используется описание анализируемого поля электронной плотности нанообъекта Cl2O в формате TXT – файла. Описание структуры формата представлено на Рис.5.20.
Отметим, что это описание предварительно может быть получено из описания поля электронной плотности данного нанобъекта, представленного в формате OUT – файла с помощью программы MacMolPlt [8].
Результатом работы рассматриваемой программы визуализации является анимационное проекционное графическое изображение совокупности полупрозрачных изоповерхностей поля (объемная визуализация). Пример такого изображения показан на Рис.5.21
Рис.5.21. Анимационное графическое изображение поля электронной плотности нанообъекта CL2O
Программа написана на языке MaxScript, при ее работе используются компоненты комплекса 3ds Max и его функциональные расширения плагины MDSpace, ElectronDens. Задаваемыми параметрами в программе являются значение поля, штатные атрибуты рендеринга. При помощи этой программы решается задача анализа поля электронной плотности исследуемого нанообъекта.
Разработанные прикладные программы визуализации позволяют осуществлять визуализацию результатов компьютерного моделирования при использовании программ моделирования, в которых исходно не предусмотрена визуализация (например, Gamess), либо использоваться для расширения имеющихся штатных функциональных возможностей визуализации в используемой программе моделирования (например, HyperChem).
Разработанные прикладные программы визуализации наноструктур, которые могут использоваться как на локальном компьютере, так и в сети Интернет, в настоящее время объединены в библиотеку, доступ к которой осуществляется с помощью программного каталога, располагаемого на локальном компьютере или в сети Интернет. Интерфейс каталога представлен на Рис. 5.22
Рис.5.22 Интерфейс библиотеки прикладных программ визуализации наноструктур
В дальнейшем планируется расширение как самого комплекса инструментальных программных средств научной визуализации, так и библиотеки прикладных программ визуализации, использующих этот комплекс. В отношении комплекса предполагается функциональное расширение уже существующих его компонентов, а также создание новых.
5.4. Прикладная программа визуализации экономических данных
В данном параграфе рассмотрен анализ финансово-экономических показателей ряда кредитных организаций и осуществлено выделение отличающихся кредитных организаций с использованием интерактивного визуального интерфейса.
Исходные данные
Исходные табличные данные о деятельности рассматриваемых кредитных организаций представляют собой многомерные табличные данные, где число столбцов n и строк m составляют несколько десятков и несколько сотен соответственно. Каждая строка таблицы соответствует одной из этих организаций и в ней содержатся упорядоченные по столбцам значения соответствующих параметров, характеризующих деятельность этой организации. Эти данные были получены из открытых источников, и представляют собой статистические данные, являющиеся результатом мониторинга этих организаций в течение 13 месяцев. Анализ этих данных позволяет получать разнообразную и обильную информацию о деятельности как отдельных, так и групп кредитных организаций.
В данной работе проводился поиск интересующей аналитиков информации о схожести (подобии) и различии отдельных строк (и соответствующих кредитных организаций), а также информация об отдельных параметрах рассматриваемых строк.
Обработка исходных данных (Filtering)
Первичная обработка данных осуществлялась в несколько этапов, причем это делалось для каждой из 13-ти таблиц. На первом этапе была осуществлена интерполяция недостающих значений по времени, там, где это было возможно. Была выбрана линейная интерполяция. Если для 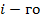

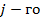
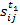

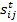
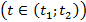
Проведенная таким образом интерполяция позволила определить часть не заданных изначально данных. Фрагмент результирующих табличных данных, соответствующих июню месяцу 2014-го года, представлен на рис.5.23.
Рис. 5.23. Фрагмент результирующих табличных данных
Вторым этапом обработки и восполнения данных являлось окончательное избавление от неполноты исходных данных для всей совокупности 13-ти таблиц. Для этого вычислялся коэффициент полноты для каждой кредитной организации.
где N-количество параметров, T-количество временных срезов (таблиц), а 
Если коэффициент полноты 
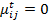
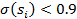
Третий этап заключался в уменьшении количества кредитных организаций для последующего анализа. Было принято решение убрать все кредитные организации, параметр «капитал» которых равен нулю. В результате получены таблицы, содержащие 40 столбцов и 81 строку.
Четвертый этап обработки и восполнения данных заключался в удалении (для каждой из 13-ти рассматриваемых таблиц) параметров, которые не являлись интегральными. Так, например, были удалены параметры «активы нетто основные средства и нематериальные активы», «активы нетто, выданные МБК», т.к. они включены в интегральный параметр «активы нетто».
Последней операцией обработки и восполнения данных была их нормализация и сведение к промежутку [0;100].
Фрагмент результирующих табличных данных, соответствующих июню месяцу 2014-го года, представлен на рис. 5.24.
Рис. 5.24. Фрагмент данных, полученных на четвертом этапе обработки и восполнения данных
Таким образом, в результате выполнения первичной обработки были получены табличные данные, меньшей размерности по сравнению с исходными, включающие 81 строку и 9 столбцов в каждой из 13-ти таблиц. Эти табличные данные в дальнейшем подвергались процедуре анализа.
Геометризация и мэппинг
Как было отмечено выше, авторов в процессе анализа интересовала информация о схожести (подобии) отдельных строк (и соответствующих кредитных организаций), а также информация об отдельных параметрах схожих строк. При этом в качестве таких строк использовались строки 13-ти таблиц отфильтрованных данных. В качестве количественного критерия различия введем меру различия кредитных организаций:
где x, y — кредитные организации xi, yi — их параметры, а i изменяется от 1 до 9.
Для решения поставленной задачи проводится геометрическая интерпретация. Кредитным организациям (строкам таблицы) были поставлены в соответствие многомерные точки, а параметрам организаций — координаты этих многомерных точек. Мера различия кредитных организаций соответственно интерпретировалась как евклидово расстояние между точками многомерного пространства (чем больше расстояние, тем больше различаются организации). При такой интерпретации, задаче анализа схожести и различия кредитных организаций ставилась в соответствие задача анализа расстояния между точками n-мерного пространства.
Для анализа расстояния между точками n-мерного пространства использовалось визуальное отображение этих точек. В начале осуществлялось проецирование исходного множества точек на одно из трехмерных пространств. При этом:
Затем выполнялось графическое проецирование сфер и цилиндров на картинную плоскость с последующим их визуальным анализом.
Результирующая совокупность сфер и цилиндров образовывала так называемую пространственную сцену с заданной геометрией и оптическими (цветовыми) характеристиками.
Таким образом, визуальный анализ пространственной сцены позволял судить о расстоянии между исходными многомерными точками. В процессе решения задачи анализа предлагалось задание в начале исходного большого значения d, а затем проводить его уменьшение и выделять подмножества многомерных точек в зависимости от получаемого изображения на картинной плоскости.
В зависимости от расстояния между точками ρ(x, y) и параметра d, изменяемого во время анализа, можно визуально выделять следующие подмножества многомерных точек:
Отметим, что выделение сгустков и квазиудаленных точек осуществляется человеком в процессе решения указанной выше задачи анализа. Таким образом, для решения задачи используется метод проекции отрезков разобранный в главе 3 «Многомерная научная визуализация».
Используемое программное средство
Для решения указанной выше задачи анализа расстояния между точками n-мерного пространства был предложен интерактивный алгоритм, блок-схема которого представлена на рис. 5.25.
Рис. 5.25. Фрагмент данных, полученных на четвертом этапе обработки и восполнения данных
Данный алгоритм был реализован на языке maxscript.
Проведение анализа
Макроанализ
Под макроанализом в данной работе понимается разбиение исходного множества точек на подмножества с конечной целью выделения подмножества удаленных точек. Алгоритм работы с программным средством предполагает задание исходного значения d большим, а затем уменьшение параметра d и выделение удаленных точек.
Рассмотрим пример решения задачи макроанализа для случая заданной 81 многомерной точки в 9-мерном пространстве. В качестве трехмерного пространства, на которое осуществлялось проецирование многомерных точек, было выбрано пространство (X1,X2,X3)
На рис. 5.26 представлено графическое проекционное изображение пространственной сцены при d=200. Видно, что все сферы соединены между собой и, значит, соответствующие им многомерные точки образовали кластер. Это значение d будет использоваться в качестве исходного и в дальнейшем его необходимо будет уменьшать.
Рис. 5.26. Графическая проекция пространственной сцены при d=200
На рис. 5.27 представлено графическое проекционное изображение пространственной сцены при d=120. Видно, что две сферы отсоединились от остальных и соответствующие им две многомерные точки образовали второй кластер. Судя по цвету цилиндра, близкому к ярко-синему, расстояние между этими точками близко к d. Отметим их синим цветом.
Рис. 5.27. Графическая проекция пространственной сцены при d=120
На рис. 5.28 представлено графическое проекционное изображение пространственной сцены при d=100. Две синие сферы обведены белым цветом. Цилиндрическая связь между ними пропала, а значит расстояние между соответствующими им точками больше 100. При этом d точки стали удаленными. Данные точки не будут влиять на дальнейший ход макроанализа. Исходя из цвета цилиндрических связей остального множества, можно сделать вывод, что одна из точек является квазиудаленной и, очевидно, при небольшом изменении d станет удаленной.
Рис. 5.28. Графическая проекция пространственной сцены при d=100
На рис. 5.29 показано графическое проекционное изображение пространственной сцены при d=70. Получившуюся при этом d сферу, соответствующую удаленной точке, отметим голубым цветом (она обведена белым цветом). Данная точка не будет влиять на последующее разбиение множества точек на подмножества.
Рис. 5.29. Графическая проекция пространственной сцены при d=70
При уменьшении d до 60, отделяется ещё одна сфера, которая отмечена желтым цветом. На рис. 5.30 представлено проекционное изображение пространственной сцены при данном d, а сфера обведена белым цветом
Рис. 5.30. Графическая проекция пространственной сцены при d=60
При продолжении анализа аналогичным образом, можно выделить последующие отделяющиеся сферы, соответсвующие удаленным многомерным точкам.
В таблице 5.1 представлены некоторые последующие значения параметра d, при которых произошло образование удаленных многомерных точек.
Таблица 5.1. Зависимость d и цвета сфер для удаленных многомерных точек.
| d при котором произошло изменение | Цвет отделяемых сфер удаленных многомерных точек |
| 34.5 | Зеленый |
| 34 | Розовый |
| 26.3 | Красный |
В процессе макроанализа было выделено 7 удаленных многомерных точек при изменении d в диапазоне от 200 до 26.
Микроанализ
Микроанализ заключался в покоординатном сравнении удаленных точек, выделенных в процессе решения задачи макроанализа.
Плоские графические проекции многомерных точек
При построении плоской графической проекции (Xi,Xi) многомерной точки, можно оценить вклад координаты в расстояние между этой точкой и остальными многомерными точками, чтобы узнать — вызвано ли удаление точки от основного множества большим значением какой то одной или нескольких координат, или же оно вызвано большими значениями всех координат рассматриваемой многомерной точки.
Построению такой проекции совокупности рассматриваемых многомерных точек предшествовало проецирование этих многомерных точек на трехмерное пространство (Xi, Xi, Xi) так, что многомерным точкам ставились в соответствие сферы, которым задавались цвета, ранее закрепленные нами за многомерным точкам в процессе решения задачи макроанализа.
В рамках рассматриваемого примера анализа взаимного расположения 81-ой многомерных точек в 9-мерном пространстве, на рис. 5.31 представлена графическая проекция на плоскость (X1,X1) всех многомерных точек, в том числе 7-и ранее найденных удаленных точек (выделены белым). На этой проекции видно, что соответствующие этим точкам 7 сфер отходят от основного сгустка, но одна из сфер (ID=1000) находится в удалении от всех остальных. Это значит, что данная координата вносит большой вклад в расстояние между этой многомерной точкой и всеми остальными.
Рис. 5.31. Графическая проекция (X1,X1), по которой можно судить о вкладе координаты X1 (просроченная задолжность в кредитном портефеле) в расстояние между удаленными точками и точками сгустка
На рис. 5.32 представлена графическая проекция всех многомерных точек на плоскость (X8,X8). На этой проекции все сферы, соответствующие удаленным точкам, находятся в тех же квадратах, что и сферы, соответствующие точкам основного сгустка, а значит, данная координата практически ничего не вносит в расстояние между точками.
Рис. 5.32. Графическая проекция (X8,X8), по которой можно судить о вкладе координаты X1 (активы нетто) в расстояние между удаленными точками и точками сгустка
В данном параграфе был рассмотрен пример анализа экономических данных с помощью интерактивного визуального интерфейса. В результате данного анализа были получены сужения об удаленных точках (аномальных объектах) и о том, каке координаты (параметры) вносят большой вклад в расстояния между объектами.