датчик с кодом грея
Инкрементные (квадратурные) и абсолютные энкодеры. Код Грея.
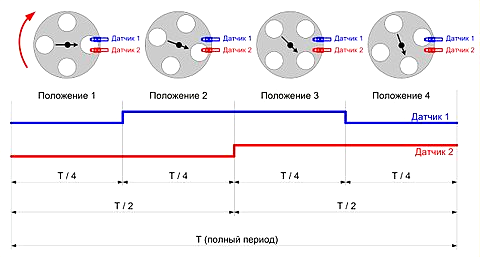
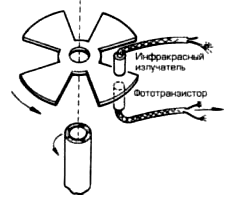
С помощью одного светодиода и одного фототранзистора можно измерять скорость вращения или перемещение без учета направления вращения. Такой датчик сложно назвать энкодером, так как, при реверсе нет возможности точно определить положение или направление вращения. Это просто датчик скорости вращения.

Энкодеры подразделяются на инкрементальные энкодеры (квадратурные энкодеры) и абсолютные энкодеры. Инкрементальные энкодеры, формируют импульсы, по которым принимающее устройство определяет текущее координаты путем подсчета числа импульсов. Для привязки системы отсчета к началу координат инкрементальные датчики перед началом работы должны быть установлены в начальное положение.
В старых компьютерных мышках, в которых применялся шарик, присутствовали два аналогичных энкодера. В них использовались специальные фототранзисторы «2 в одном»:

В нашей конструкции мы используем два отдельных фототранзистора:


Иногда требуется знать положение сразу после включения устройства. Т.е. нет технической возможности вывести устройство в исходное положение и затем по количеству «кликов» оценить положение.
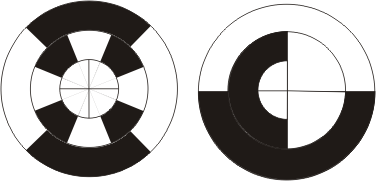
Исходный растр диска:
разбит на два диска:
Между дисками установлена двусторонняя плата со светодиодами, за дисками фототранзисторы. Таким образом были уменьшены габариты.

Внимательный читатель мог заметить, что растр кодового диска абсолютного энкодера не соответствует обычному двоичному коду. В энкодерах применяют специальный код Грея.
Что такое код Грея? Представьте себе некоторое устройство, скажем датчик положения, которое выдает положение в двоичном виде по трем проводам. На выходе могут быть следующие комбинации в двоичном коде:
000 001 010 011 100 101 110 111
Задача о ранце и код Грея
Не так давно на Хабре была статья «Коды Грея и задачи перебора». Статья эта скорее, математическая, нежели программистская, и мне, как простому программисту, читать её было невыносимо тяжело. Но сама тема мне знакома, поэтому я решил описать её своим взглядом, а так же рассказать о том, как использовал её в решении задачи о ранце.

КДПВ: задача о ранце на живом примере
Предыстория
Всё началось 10 лет назад, когда я учился в девятом классе. Я случайно подслушал разговор учителя по информатике, рассказывающего задачку кому-то из старших: дан набор чисел, и ещё одно число — контрольное. Надо найти максимальную сумму чисел из набора, которая не превышала бы контрольное число.
Задача почему-то запала мне в душу. Вернувшись домой, я быстро накатал решение: наивный перебор всех возможных сумм с выбором наилучшего. Сочетания я получал, перебирая все N-разрядные двоичные числа и беря суммы тех исходных чисел, которым соответствуют единицы. Но я с огорчением обнаружил, что при количестве элементов начиная где-то с 30, программа работает очень долго. Оно и не удивительно, ведь время работы такого алгоритма — n*2 n (количество сочетаний, умноженное на длину суммы).
Прошло 5 лет. Я успел закончить школу и поступить в университет, но эта задача по-прежнему была со мной. Один раз, листая книгу «Алгоритмические трюки для программистов» (Hacker’s Delight / Henry S. Warren Jr.), я наткнулся на описание кода Грея: это последовательность двоичных чисел, каждое из которых отличается от предыдущего только одним битом. «Стоп!» — подумал я — «Это означает… Да! Это означает, что в той самой задаче на каждом шаге перебора можно не считать сумму целиком, а лишь добавлять или вычитать одно число». И я тут же углубился в изучение темы.
Построение кода Грея
Код Грея можно построить для числа любой разрядности. Для одного разряда он очевиден:
Чтобы добавить второй разряд, можно к этой последовательности дописать такую же задом наперёд
и ко второй половине дописать единицы:
Аналогично для трёх разрядов:
Такой код, полученный отражением кода меньшей разрядности, называется рефлексным (отражённым) кодом Грея. Бывают и другие последовательности, но на практике обычно используется именно эта.
Этот код назван в честь Фрэнка Грея, который изобрёл ламповый АЦП, выдававший цифровой сигнал именно в этом коде. При небольших изменениях уровня входного сигнала цифровой выход мог измениться только в одном бите, и этим исключались резкие скачки из-за неодновременного переключения битов.

Иллюстрация патента Фрэнка Грея
Самое наглядное применение кода Грея — в датчиках угла поворота. Датчик, аналогичный тем, что был в старых механических мышах, но определяющий не относительное смещение, а абсолютное значение угла. Для этого на каждый датчик нужно несколько оптопар и несколько щелевых решёток. Причём каждое следующее положение датчика должно отличаться от предыдущего только состоянием одного бита, иначе на границах возможно несинхронное переключение битов, и следственно — резкие скачки в показаниях прибора. Здесь видна любопытная особенность кода Грея: последнее число также отличается от первого одним битом, поэтому его можно «закольцевать».

Датчик абсолютного угла поворота. Оптические щели расположены в соответствии с кодом Грея
Применение в задаче о ранце
Но вернёмся к задаче о ранце. Стандартная формула даёт нам код Грея по номеру:
По ней мы можем только посчитать сумму все нужных элементов. А мы собирались на каждой итерации добавлять или вычитать одно значение, верно? Значит, нам нужно получить номера изменяемых битов. Для многоразрядных чисел эти номера будут такими:
Ничего не напоминает? Это номер бита, который мы устанавливаем в единицу, когда просто перечисляем обычные двоичные числа. Или иначе — номер младшей единицы в двоичном числе. Эта операция называется find first set и в большинстве процессоров существует в виде отдельной инструкции. Visual C++ предоставляет эту инструкцию в виде функции _BitScanForward.
Итак, теперь мы готовы написать программу, решающую задачу о ранце через код Грея. Сформулируем задачу так:
В файле input.txt в первой строке указана вместимость рюкзака, а в остальных строках — размеры вещей. В консоль нужно вывести максимальную загрузку рюкзака и размеры выбранных вещей. Проверку корректности ввода и пр. — нафиг.
Мы будем хранить битовую маску использованных вещей, и по мере необходимости добавлять или убирать одну из них. Чтобы обойтись int-ами, ограничим количество вещей (и используемых бит) тридцатью одной.
Прощу прощения за возможные шероховатости; к сожалению, C++ уже давно не мой профильный язык.
Работает действительно быстрее, чем сборка с нуля всех сумм, разница заметна уже при 20 числах, а при 30-и я так и не дождался выполнения наивного алгоритма, в то время как новый вариант выполняется за 7 секунд. Впрочем, учитывая экспоненциальную сложность, это совсем не мало: для 50 чисел использовать этот алгоритм уже нет смысла. К сожалению, любой точный алгоритм будет работать не быстрее, чем за 2 n ; быстрее возможно только приблизительное решение. (Апдейт: в некоторых случаях динамическое программирование и meet-in-the-middle решают задачу быстрее; подробности см. в комментариях.)
Наверное, именно поэтому я обречён до конца жизни нести свой ранец, пытаясь ускорить эту программу. Я уже однажды переписывал цикл на ассемблере, получив небольшой прирост в скорости, а сейчас даже подумываю сделать многопоточную версию программы. Вам же остаётся лишь мне посочувствовать. 🙂
Энкодеры
Датчики углового и линейного перемещения, датчики наклона
Инкрементальные энкодеры
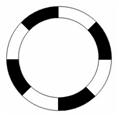
Инкрементальный энкодер (Incremental Encoder) регистрирует относительное перемещение (приращение). Разрешение (Resolution) углового энкодера определяется количеством импульсов на один оборот (на рисунке изображён оптический дик с разрешением 8 имп/об).
Частота импульсов на выходе энкодера пропорциональна скорости вращения.
Система управления должна подсчитывать импульсы, чтобы вычислить угол поворота энкодера относительно точки отсчёта.
В системах, работающих с абсолютными координатами (станок с ЧПУ), перед началом работы (после включения питания) необходимо выставить ноль – вывести рабочий орган машины в опорную (реперную) точку и в ней обнулить счётчик импульсов.
Синусно-косинусные инкрементальные датчики положения sin/cos 1-Vss и 1-Vpp
Датчики с интерфейсом 1-Vpp используются в сервосистемах, т.к. как позволяют получать очень высокое разрешение. Так, например, если датчик выдаёт 2048 периодов синусоиды (импульсов) на оборот, а система управления в каждой такой синусоиде различает 2048 дискретных уровней, то общее разрешение датчика составит 2048 х 2048 = 4194304 импульсов на оборот.
Инкрементальные датчики с интерфейсом TTL или HTL
Абсолютные энкодеры
Разрешение абсолютного энкодера (Absolute Encoder) определяется количеством уникальных кодов на один оборот. Однооборотные (Single-turn) абсолютные энкодеры определяют положение в пределах одного оборота, многооборотные (Multi-turn) – в пределах определённого числа оборотов.
Абсолютные датчики положения не требуют для начала работы выхода в опорную точку – при включении питания датчик сразу определяет координату, сканируя кодовые дорожки.
Резольверы
Резольвер (Resolver) – это аналоговый электромагнитный абсолютный однооборотный датчик, работающий по принципу вращающегося электрического трансформатора.
Резольверы отличаются высокой надёжностью (они не бьются и не запотевают, как оптические) и точностью (аналоговые, а не дискретные).
Код Грея
Код Грея (Gray Code) – это двоичный код, в котором два соседних значения отличаются только одним разрядом.
| Десятичное число | Двоичное число | Код Грея |
|---|---|---|
| 0 | 000 | 000 |
| 1 | 001 | 001 |
| 2 | 010 | 011 |
| 3 | 011 | 010 |
| 4 | 100 | 110 |
| 5 | 101 | 111 |
| 6 | 110 | 101 |
| 7 | 111 | 100 |
Формула побитного преобразования двоичного кода в код Грея
Gi = Bi⊕Bi+1,
биты нумеруются справа налево, ⊕ – исключающее ИЛИ (если биты равны, то результат равен 0; если биты не равны, то результат равен 1).
Код Грея используется для кодирования положений в абсолютных датчиках, так как обладает большей помехозащищённостью, чем обычное двоичное кодирование (Natural Binary).
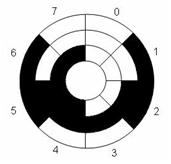
На рисунке изображён оптический диск с 3-х разрядным (8 положений) кодом Грея.
Тахогенераторы
Тахогенераторы предназначены для определения скорости и направления вращения. Напряжение на выходе тахогенератора пропорционально скорости вращения вала.
Как выбрать
Датчики линейного и кругового перемещения
Датчики угла наклона (инклинометры)
Про геометрический смысл кодов Грея
Коды Грея имеют близкую родственную связь с кривой Гильберта.
Впрочем, при общении с коллегами выяснилось, что эта несложная зависимость выглядит в их глазах как нечто нетривиальное. Поиск в интернетах навскидку ничего не дал кроме мутной фразы в вики: “кривые Гильберта в пространствах большей размерности являются представителями обобщений кодов Грея”. Поэтому возникло желание раскрыть тему — коротенько, простым языком.
В результате под катом — «скандалы, интриги, расследования».
Основная особенность кода Грея — два соседних в лексикографическом порядке значения отличаются только в одном разряде. С другой стороны, кривая Гильберта непрерывна — расстояние между двумя соседними точками всегда единица. Уже только одно это намекает об их внутренней связи.
Код Грея описывает похождения кривой Гильберта в рамках единичного гиперкуба. В самом деле, если взять 3-разрядный код и нарисовать его в 3-мерном пространстве (принимая каждый разряд за соответствующую координату), получим
Фиг.1 3-разрядный код Грея как 3-мерный куб
Знакомая картина — это 3-мерный симплекс кривой Гильберта! Последовательно заменяя каждый узел симплекса на такой же симплекс (с учетом поворотов и отражений для сохранения непрерывности), получим кривую Гильберта 4х4х4.
Продолжая эти итерации, сможем непрерывно заполнить кубическую решетку любого размера.

Фиг.2 несколько итераций симплекса кривой Гильберта.
Но как так получилось?
Известно, что код Грея самоподобен. Его иногда называют зеркальным “из-за того, что первая половина значений при изменении порядка эквивалентна второй половине, за исключением старшего бита. Старший бит просто инвертируется”. Для наглядности, 3-разрядный код — самый старший разряд — самый левый:
Раз уж речь зашла о самоподобии, начнём с начала — с одноразрядного кода. Строго говоря, можно было бы начать и с нулевой размерности — точки, принципиально это ничего не меняет, просто слов пришлось бы написать больше.
Одноразрядный код Грея даже проще, чем трёхлинейная винтовка, он либо 0, либо 1.
Геометрически это соответствует одномерному единичному кубу — отрезку. По отрезку можно двигаться либо из начала в конец, либо из конца в начало — с точностью до симметрии это одно и то же. Но всё же, началом будем называть то место, где значение меньше (вспомним, что стороны куба это разряды числа), а концом — где больше.

Фиг.3 Первые две итерации “миссионерского” варианта
Здесь красным цветом выделена предыдущая итерация, синим — её клон, бирюзовым — их соединение.
Обратим внимание — соединение всегда проходит по единственной размерности — вновь добавленной, отсюда в силу самоподобия и появляется основная особенность кода Грея. А раз соединяется конец предыдущей итерации с концом её клона, возникает “зеркальность” — при обходе, клон мы вынуждены проходить в обратном порядке. Вне зависимости от размерности. Здесь же видно происхождение и особенности кривой Гильберта — как бы ни была велика решетка (любой размерности), на низовом уровне это всё тот же единичный куб с переходами длиной в единицу.

Фиг.4 Первые две итерации варианта “паровозик”, те же цвета
А ведь и эта музыка нам знакома — получился симплекс Z-кривой. Слово симплекс здесь также означает, что если взять каждую его точку и заменить на симплекс, получим куб 4х4х4, продолжая итерации — можно заполнить сколь угодно большую кубическую решетку.
Забавно, что в этом случае преобразование пройденного от начала координат пути в код, который может быть разобран на разряды-координаты тривиально.
Тогда как случае кода Грея это G = W ^ (W >> 1), где W-пройденная длина, G — код Грея.

Фиг.5 первые две итерации Z-кривой (wiki)

Фиг.6 для сравнения, первые две итерации кривой Гильберта (wiki)
А ведь других то (естественных) вариантов обхода единичного гиперкуба и нет.
Вот и получается, что куда ни кинь, кругом Гильберт, Лебег … и пустота.
PS: на титульной картинке круговой энкодер с восьмиразрядным кодом Грея.
PPS: тут меня поправляют, что симплекс — вполне устоявшийся термин, нехорошо с ним так. Что-же, в данной статье ведь не просто симплекс, а симплекс кривой Гильберта или симплекс Z-кривой. Пусть правоверные математики меня простят.
Принцип работы абсолютного энкодера

Всё о абсолютных энкодерах. От А до Я: виды цифровых кодов, особенности кодирования/декодирования сигналов в абсолютных энкодерах, описание работы абсолютного энкодера, конструкция одно- и многооборотного энкодера, терминология используемая в тех. документации на абсолютные энкодеры. Абсолютный или инкрементальный? Когда оправдано или неизбежно применение абсолютного энкодера.
Абсолютные энкодеры от А до Я
Для чего вообще нужен абсолютный энкодер?
В машино- и станкостроении для осуществления правильного позиционирования систем контроля за передвижением постоянно требуются самые последние и точные позиционные данные. Благодаря своей способности в любой момент осуществлять присвоение точных и однозначных позиционных значений какой-либо угловой позиции или позиции перемещения абсолютные энкодеры стали одним из самых важных соединительных звеньев между механической частью машины и ее блоком управления.
История создания первого абсолютного энкодера вращения и основные отличия от инкрементного
Первый абсолютный датчик, принцип работы которого основывался на оптоэлектронном считывании закодированных растров, был разработан немецкой компанией FRABA в 1973 году. В то время как инкрементальные датчики определяют положение только относительно какого-то определенного положения, в абсолютных датчиках информация о угловом положении закодирована механически, например на оптическом диске в виде растра содержащего уникальный код для каждой позиции вала. Таким образом абсолютный энкодер выдает информацию о положении вала, т.е. о текущей координате, сразу после включения и формирует сигнал как во время вращения, так и в режиме покоя.
Абсолютный энкодер не теряет своего значения при потере питания и, если в обесточенном состоянии вал энкодера был провернут на определенный угол или какое-то количество оборотов, то при появлении напряжения энкодер сразу выдаст новое, фактическое угловое положение вала и фактический номер оборота. Благодаря этому свойству не требуется после каждого включения системы производить движение механических частей машины на стартовую или как принято называть референтную позицию, что является неоспоримым преимуществом абсолютных энкодеров перед инкрементальными (импульсными).
Преимущества абсолютного энкодера
Преимуществом абсолютного энкодера является также и то, что он не подвержен помехам. В случаях, когда сигнал с диска не может быть полноценно прочитан энкодером, например, если вал вращается слишком быстро, точный угол поворота будет зарегистрирован, когда скорость вращения уменьшится. Но даже при быстром вращении вала возможна регистрация положения, хоть и с меньшей точностью. Для этого во внимание просто принимается только информация поступающая от более старших разрядов, т.е. искаженная (за счет большой скорости вращения) информация поступающая от младших разрядов просто игнорируется. Абсолютный энкодер устойчив к вибрациям и другого рода помехам, т.к. ошибка в результате подсчета «ложных» импульсов, возникших в результате, например, вибрации, исключена.
Для более четкого понимания принципа работы абсолютных энкодеров, в частности основания для необходимости использования специальных способов кодирования сигналов при построении абсолютных энкодеров, будет уместно вспомнить некоторые основы цифровой техники, в т.ч. виды/методы кодирования чисел/сигналов описанных ниже.
Виды цифровых кодов и особенности их использования в системах позиционирования
Бинарные коды
Термин «бинарный» по смыслу — состоящий из двух частей, компонентов. Таким образом бинарные коды это коды которые состоят только из двух символьных состояний например черный или белый, светлый или темный, проводник или изолятор. Бинарный код в цифровой технике это способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы БК называют битами. Одним из обоснований применения БК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства светового потока при считывании с оптического кодового диска.
В таблице ниже представлены две основные возможности кодирования — двоичное кодирование и кодирование по методу Грея (который далее будет описан подробнее), а также способы представления информации в различных системах счисления.
Для разных систем счисления в таблице используются следующие сокращения:
десятичное число = decimal = DEC
двоично-десятичное число = binary code decimal = BCD
шестнадцатеричное число = hexadecimal = HEX
Обычное двоичное кодирование
| DEC | BCD (Binary) | HEX |
|---|---|---|
| 0 | 0000 | 0h |
| 1 | 000 1 | 1h |
| 2 | 00 10 | 2h |
| 3 | 001 1 | 3h |
| 4 | 0 100 | 4h |
| 5 | 010 1 | 5h |
| 6 | 01 10 | 6h |
| 7 | 011 1 | 7h |
| 8 | 1000 | 8h |
| 9 | 100 1 | 9h |
| 10 | 10 10 | Ah |
| 11 | 101 1 | Bh |
| 12 | 1 100 | Ch |
| 13 | 110 1 | Dh |
| 14 | 11 10 | Eh |
| 15 | 111 1 | Fh |
Кодирование в коде Грея
| DEC | BCD (Gray) | HEX |
|---|---|---|
| 0 | 0000 | 0h |
| 1 | 000 1 | 1h |
| 3 | 00 1 1 | 3h |
| 2 | 001 0 | 2h |
| 6 | 0 1 10 | 6h |
| 7 | 011 1 | 7h |
| 5 | 01 0 1 | 5h |
| 4 | 010 0 | 4h |
| 12 | 1 100 | Ch |
| 13 | 110 1 | Dh |
| 15 | 11 1 1 | Fh |
| 14 | 111 0 | Eh |
| 10 | 1 0 10 | Ah |
| 11 | 101 1 | Bh |
| 9 | 10 0 1 | 9h |
| 8 | 100 0 | 8h |
Двоично-десятичный код (Binary code decimal)
Двоично-десятичный код является широкораспространенным кодом, который может обрабатываться непосредственно микропроцессором и является основным кодом для обработки цифровых сигналов. Двоично-десятичный код состоит только из 0 и 1.
Наибольшее число, которое может быть выражено двоичным кодом, зависит от количества используемых разрядов, т.е. от количества бит в комбинации, выражающей число. Например, для выражения числовых значений от 0 до 7 достаточно иметь 3-разрядный, т.е. 3-битовый код.
Двоично-десятичный код является многошаговым кодом. Это означает, что при переходе от одного положения (значения) в другое могут изменяться несколько бит одновременно. Например, число 3 в двоичном коде = 011. Число же 4 в двоичном коде = 100. Соответственно, при переходе от 3 к 4 меняют свое состояние на противоположное все 3 бита одновременно. Считывание такого кода приводит к тому, что из-за несовершенства считывателя, например, из-за неизбежных отклонений (допусков) при производстве кодового диска, изменение информации от каждой из дорожек в отдельности никогда не происходит одновременно. Как следствие, при переходе от одного числа к другому, кратковременно (или постоянно в случае остановки вала энкодера непосредственно на критическом участке перехода!) выдается неверная информация о положении вала. Так, на участке вышеупомянутого перехода от числа 3 к числу 4 очень вероятна выдача числа 7, когда, например, старший бит во время перехода поменял свое значение немного раньше чем остальные. Таким образом, использование обычного двоичного кода может с большой вероятностью приводить к выдаче числа, далёкого от реального значения, и, как следствие, непредсказуемому реагированию системы управления или контроллера на искаженный сигнал энкодера. Чтобы избежать этого применяется так называемый одношаговый код, например, код Грея.
Код Грея (Gray code)
Код Грея (Gray code — назван в честь американского физика Frank Gray) идеально подходит для систем механического позиционирования, в т.ч. абсолютных энкодеров. Код Грея предпочтительнее обычного двоичного тем, что обладает свойством постоянства бинарной комбинации: изменение кодируемого числа на единицу соответствует изменению кодовой комбинации только в одном разряде. Таким образом, Грей-код является так называемым одношаговым кодом. Он строится на базе двоичного по следующему правилу: старший разряд остается без изменения, а каждый последующий разряд инвертируется, если предыдущий разряд исходного двоичного кода равен единице.
Из таблицы выше видно, что число представленное кодом Грея, при переходе от одного числа к другому (соседнему), меняет свое состояние лишь в одном разряде информации, в то время, как в двоичном коде могут поменять свое состояние несколько разрядов (бит) одновременно. Биты меняющие свое состояние, при переходе от одного числа к другому, в таблице обозначены красным цветом.
В случае использования кода Грея погрешность при считывании информации на участке перехода от одного числа к другому приведет лишь к тому, что этот переход будет лишь несколько смещен по времени, однако выдача совершенно неверного значения углового положения на участке перехода полностью исключается. Это особенно актуально для датчиков, где носителем / источником информации (например, о положении вала энкодера) является механический элемент. В случае абсолютного энкодера это оптический диск с механически нанесенными на него метками, где минимальные геометрические погрешности / смещения нескольких оптических дорожек / секторов относительно друг друга не исключаются из-за погрешностей офсетной печати при производстве на стадии нанесения рисунка на оптический диск. На картинке ниже представлен диск энкодера с рисунком (растром) в формате Грей-кода.
Преимуществом Грей-кода является также его способность зеркального отображения информации. Так, инвертируя старший бит можно простым образом менять направление счета. Эту функцию выполняет, так называемый, вход «Complement». В зависимости от потенциала на этом входе выдаваемое энкодером значение будет возрастающим или спадающим при одном и том же физическом направлении вращения оси.
Поскольку информация, выраженная в коде Грея, имеет чисто кодированный характер, не несущей реальной числовой информации, его необходимо перед дальнейшей обработкой сперва преобразовать в стандартный бинарный (двоичный) код. Преобразование кода Грея в привычный бинарный код можно осуществить программно (в контроллере) или используя простую схему с инверторами и логическими элементами «исключающее или» (XOR) как показано на схеме ниже:
Примечание:
*Код Грея может логически преобразовываться в двоичный код когда терминал Vin подключается к 0 V.
**Инвертор
***Исключающее или
Gray-Excess-Code
Обычный одношаговый Грей-код подходит для разрешений, которые могут быть представлены в виде числа возведенного в степень 2. В случаях, где надо реализовать другие разрешения из обычного Грей-кода, вырезается и используется средний его участок. Таким образом, сохраняется «одношаговость» кода. Однако числовой диапазон начинается не с нуля, а смещается на определенное значение. При обработке информации от генерируемого сигнала отнимается половина разницы между первоначальным и редуцированным разрешением. Такие разрешения как, например, 360° для выражения угла часто реализуются этим методом. Так 9-ти битный код Грея равный 512 шагам, урезанный с обеих сторон на 76 шагов будет равен 360°.
Устройство оптического абсолютного энкодера
Измерительная система абсолютного оптического энкодера состоит из следующих основных компонентов:
— поворотный вал монтированный на двух подшипниках;
— кодовый оптический диск, установленный на вал;
— инфракрасный светодиод (в качестве источника света);
— опто-электронная (фототранзисторная) считывающая матрица;
— схема обработки сигнала;
— в многооборотном энкодере дополнительно встраивается редуктор из нескольких кодовых оптических дисков со светодиодами и считывающими матрицами для каждого из них.
Инфракрасные лучи светодиода просвечивают кодовый диск и попадают на фототранзисторную считывающую матрицу, расположенную с обратной стороны кодового диска. При каждом шаге углового положения кодового диска темные его участки предотвращают попадание света на те или иные фототранзисторы считывающей матрицы преобразущей световые сигналы в электрические. Электрические сигналы, в свою очередь, преобразуются электроникой энкодера в двоичный код.
Однооборотный энкодер
Однооборотными (Single — Turn) энкодерами называются датчики (энкодеры), которые выдают абсолютное значения в пределах одного оборота, т.е. в пределах оборота 360°. После одного оборота код является полностью пройденным и начинается опять с его начального значения. Эти датчики служат, преимущественно, для измерения угла поворота и применяются, например, в антенных системах, эксцентричных коленчатых прессах и т.д. и т.п..
Разрешение однооборотного энкодера определяется/обозначается количеством бит. Например, у энкодера с разрешением в 16-бит подразумевается разрешение в 65536 меток в обороте.
В свою очередь, чтобы перевести количества меток (шагов) в обороте в угловые градусы достаточно разделить 360° на количество меток, например: разрешение 65536 меток (16 бит) соответствует разрешению: 360/65536=0,005° (угловых градусов).
Ниже приведены самые распространенные разрешения однооборотного энкодера с соответствующими значениями в угловых градусах:
256 (8 Bit) — 1.4°
360 (9 Bit) — 1°
1024 (10 Bit) — 0,35°
4096 (12 Bit) — 0,088°
8192 (13 Bit) — 0,044°)
65536 (16 Bit) — 0,005°
Многооборотный энкодер
Линейные перемещения предполагают необходимым применение измерительной системы регистрирующей не только положение вала в пределах одного оборота, но и определенного количества оборотов. Например, в линейных приводах или в задачах измерения с помощью зубчатой измерительной штанги уместно применение энкодеров, где дополнительно к измерению угла поворота в пределах одного оборота (первой ступенью энкодера) также происходит регистрация количества оборотов дополнительным, своего рода редуктором (образующим вторую ступень энкодера) состоящим из нескольких кодовых оптических дисков, образуя, таким образом, многооборотный энкодер ( Multi — Turn ). Разрешение многооборотного энкодера, как правило, обозначается раздельно как разрешение в пределах одного оборота + количество оборотов в формате количества бит. Так, комбинация цифр в наименовании энкодера в виде, например, 1216 означает разрешение 12 бит оборотов (4096 оборотов) и 16 бит в обороте (65536 меток на оборот).
Магнитные абсолютные энкодеры
Принцип магнитных измерений
Магнитные энкодеры определяют угловое положение с использованием магнитно-полевой технологии. Постоянный магнит, установленный на валу энкодера, создает магнитное поле, которое измеряется датчиком, формирующим уникальное значение абсолютного положения.
Инновационная многооборотная технология
Многооборотные магнитные энкодеры IXARC POSITAL используют инновационную технологию для отслеживания количества оборотов, даже если оборот произошел при отключенном питании системы. Для выполнения этой задачи энкодеры преобразуют вращение вала в электрическую энергию. Технология основана на эффекте Виганда: когда постоянный магнит на валу энкодера поворачивается на определенный угол, магнитная полярность в „проводе Виганда“ резко меняется, создавая кратковременный всплеск напряжения в обмотке, окружающей провод. Этот импульс отмечает поворот вала, а также обеспечивает питание электронной цепи, регистрирующей данное событие. Эффект Виганда происходит в любых условиях, даже при очень медленном вращении, и исключает потребность в резервных батареях.
Особенности магнитных энкодеров
Магнитные энкодеры являются надежными, долговечными и компактными. Конструкция, не требующая использования батарей и не имеющая зубчатых передач, обеспечивает механическую простоту и более низкую стоимость по сравнению с оптическими энкодерами. Их компактные габариты позволяют использовать их в очень ограниченном пространстве.
И всё таки — оптический или магнитный?
Этот вопрос однажды задали соучредителю группы компаний «Fraba» (он же директор компании Posital) в интервью журнала «Конструктор» при обсуждении темы внедрения новой магнитной технологии при производстве энкодеров вращения.
Ссылка на перевод публикации этого интервью см. здесь в статье «Важные критерии при выборе энкодера» >>
Терминология абсолютных энкодеров
| Абсолютный, однооборотный (Singleturn) датчик угла поворота | Датчик угла поворота, который для каждой позиции вала, в пределах одного оборота, выдает однозначную, кодированную информацию. Информация о положении вала сохраняется также и при пропадании напряжения питания. |
| Абсолютный, многооборотный (Multiturn) датчик угла поворота | Датчик угла поворота, который помимо информации о положении вала в пределах одного оборота выдает также информацию о номере оборота вала. Этот датчик также полностью сохраняет информацию при пропадании напряжения питания, т.к. положение вала в пределах одного оборота и номер оборота регистрируются физически с помощью нескольких, например, оптических кодовых дисков. |
| ASI | Asynchron-Serielles-Interface. Асинхронный интерфейс с последовательной передачей данных. Аппаратная часть (драйвер) реализована по стандарту EIA RS485 или RS422. |
| ASIC | Специальная микросхема высокой интеграции, выполненная под заказ. Используется во многих энкодерах. |
| Baudrate | Частота (скорость) передачи данных последовательного интерфейса в битах в секунду. |
| CAN-Bus Multi-Master-Bus-System | Интерфейс связи, допускающий подключение к сети (двухпроводной линии связи) нескольких ведомых устройств. В настоящее время для CANopen приняты некоторые нормированные протоколы. Для датчиков угла поворота действует — DSP 406. |
| Частота смены кода (Step freqency) | Количество меток (шагов) в секунду для абсолютных энкодеров. Для датчиков с разрешением 13 бит (8192 метки) и 400 kHz частотой смены кода, максимальная электрическая частота вращения составит 3000 min-1. |
| Datavalid | Выход диагностики для перепроверки достоверности посылаемых данных. |
| Направление вращения (Complement) | Управляющий вход для установки последовательности данных. Задает направление вращения по- или против- часовой стрелки при котором данные на выходе будут при вращении возрастать. |
| Точность | Отклонение измеренного энкодером угла поворота (положения) от фактического. Точность зависит, в первую очередь, от точности нанесения рисунка кода на, например, оптический диск. Риски / секторы нанесенные на диск имеют определенную нелинейность, т.е. неравномерная плотность меток по окружности диска определяет точность энкодера (как правило в процентах). |
| Preset (Обнуление) | Управляющий вход, позволяющий обнулить показания на выходе абсолютного энкодера в любом месте во всей области разрешения без необходимости механического позиционирования вала. Для перепрограммируемого абсолютного энкодера с помощью этого входа может быть программно выставлено любое значение (Offsetwert). |
| Profibus DP | Master-Slave-Bus-System с двухпроводной линией связи и аппаратным EIA RS485 драйвером. Profibus-DP протокол специфицирован для энкодеров. |
| Resolution per revolution (Разрешение в обороте) | Для однооборотного датчика (Singleturn) указывает максимальное количество меток в пределах одного оборота. Для программируемого энкодера параметр необходимого разрешения в пределах одного оборота энкодера может задаваться пользователем программно. В этом случае энкодер пересчитывает фактическое (физическое) разрешение в более низкое. |
| Total Resolution (Общее разрешение) | Общее разрешение многооборотного (Multiturn) энкодера — указывает максимальное количество меток в пределах одного оборота и максимальное количество оборотов. Для программируемого энкодера параметр необходимого разрешения в пределах одного оборота и количества оборотов энкодера может задаваться пользователем программно. В этом случае энкодер пересчитывает фактическое (физическое) разрешение в более низкое. |
| SSI | Synchron-Serielles-Interface. Передача данных от энкодера осуществляется синхронно (бит за битом) по внешнему тактовому импульсу. |
| Takt +, Takt — | Тактовые провода линии связи SSI инерфейса для синхронной передачи данных.Takt + и Takt — образуют гальванически развязанную (от проводов питания) линию связи для приема энкодером тактового сигнала. |
| Data +, Data — | Провода данных линии связи SSI инерфейса для синхронной передачи данных.Data + и Data — образуют гальванически развязанную (от проводов питания) линию связи для выдачи энкодером сигнала данных. |
Сопутствующие товары и статьи
Абсолютные энкодеры Posital Fraba
Однооборотные и многооборотные абсолютные энкодеры производства Posital Fraba с разрешением до 31 бит и интерфейсами: — SSI, параллельный, аналоговый, CANopen, DeviceNet, EtherCAT, EtherNet/IP, Interbus, Modbus, Powerlink, Profibus DP, Profinet и др..
Принцип работы инкрементального энкодера
Описание работы инкрементального энкодера, квадратура выходных сигналов, особенности механического сопряжения, особенности оптической и магнитной технологии.
Последовательный синхронный интерфейс SSI
Подробное описание протокола / последовательного интерфейса SSI, рекомендации по подключению и общее представление шины RS485. В каких случаях оправдан параллельный интерфейс и когда более оправдано применение последовательного.
Важные критерии при выборе энкодера
Функциональные возможности, конструктивные особенности, применяемые материалы и технологии изготовления абсолютных оптических и магнитных энкодеров вращения производства. Энкодер вращения — оптический или магнитный? Перевод публикации интервью в журнале «Конструктор» с соучредителем группы компаний Fraba на тему магнитной технологии.