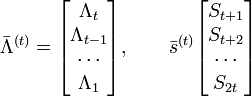
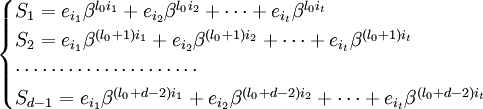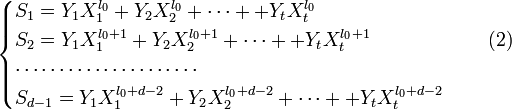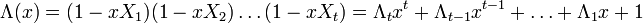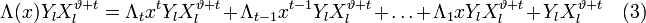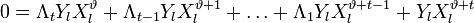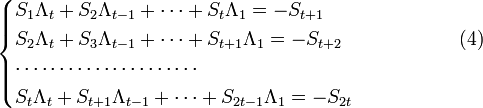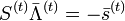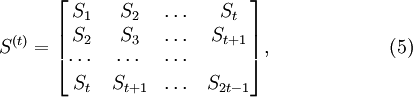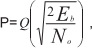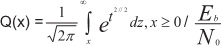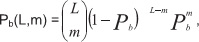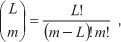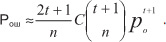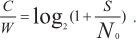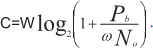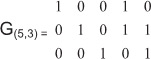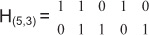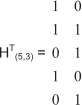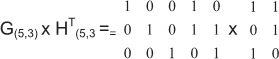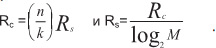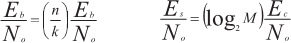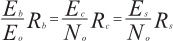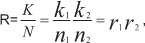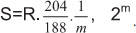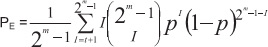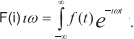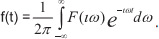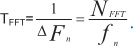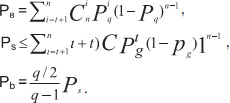декодирование бчх кодов пример

Помехоустойчивое кодирование. Коды Хэмминга

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.

Рассчитаем скорость кода для:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.

Классификация помехоустойчивых кодов

По используемому алфавиту:

Блочные коды делятся на

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.

Источник

Код БЧХ

Коды Боуза — Чоудхури — Хоквингхема (БЧХ-коды) — в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с заранее определенными корректирующими свойствами, а именно, минимальным кодовым расстоянием. Коды Рида — Соломона являются частным случаем БЧХ-кодов.

Содержание

Формальное описание

БЧХ-код является циклическим кодом, который можно задать порождающим полиномом. Для его нахождения в случае БЧХ-кода необходимо заранее определить длину кода n (она не может быть произвольной) и требуемое минимальное расстояние 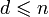. Найти порождающий полином можно следующим образом.

Построение

Для нахождения порождающего полинома необходимо выполнить несколько этапов:

Примеры кодов

Примитивный 2-ичный (15,7,5) код

16-ричный (15,11,5) код (код Рида — Соломона)

g(x) = (x − α)(x − α 2 )(x − α 3 )(x − α 4 ) = x 4 + α 13 x 3 + α 6 x 2 + α 3 x + α 10

Каждому элементу поля GF(16) можно сопоставить 4 битам, поэтому одно кодовое слово эквивалентно 60=15*4 битам, таким образом набору из 44 бит ставится в соответствие набор из 60 бит. Можно сказать, что такой код работает с полубайтами информации.

Кодирование

Для кодирования кодами БЧХ применяются те же методы, что и для кодирования циклическими кодами.

Методы декодирования

Коды БЧХ являются циклическими кодами, поэтому к ним применимы все методы, используемые для декодирования циклических кодов. Однако существуют гораздо лучшие алгоритмы, разработанные именно для БЧХ-кодов.

Алгоритм Питерсона — Горенстейна — Цирлера (ПГЦ)

.

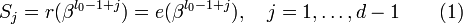
Составим полином локаторов ошибок:

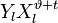
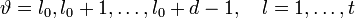
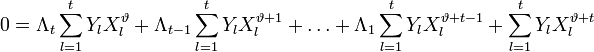
Корнями этого полинома являются элементы, обратные локаторам ошибок. Помножим обе части этого полинома на . Полученное равенство будет справедливо для :

.

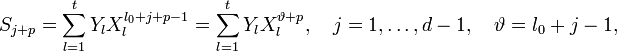
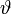
Учитывая (2) и то, что (то есть меняется в тех же пределах, что и ранее) получаем систему линейных уравнений:

Или в матричной форме

См. также

Литература

Полезное

Смотреть что такое «Код БЧХ» в других словарях:

Код Боуза — Чоудхури — Хоквингема — Коды Боуза Чоудхури Хоквингхема (БЧХ коды) в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с… … Википедия

КОД С ИСПРАВЛЕНИЕМ ОШИБОК — код, корректирующий ошибки, множество сообщений, предназначенных для передачи по каналу связи с шумами, обладающее тем свойством, что окрестность ошибок каждого сообщения (т. е. совокупность искаженных вариантов этого сообщения) не пересекается с … Математическая энциклопедия

Код Рида — Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия

БЧХ код — код Боуза Чоудхури Хоквенгема Семейство циклических двоичных кодов с исправлением ошибок. Длина кода n, определяется как 2n t, где t — пюбое целое положительное число (t > 3). Такой код позволяет исправлять t ошибок, при этом длина кода… … Справочник технического переводчика

код Бозе-Чаудхури-Хоккеигема — БЧХ код — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы БЧХ код EN Bose Chaudhuiri Hocquehgam (ВСН) code … Справочник технического переводчика

КОД С ИСПРАВЛЕНИЕМ АРИФМЕТИЧЕСКИХ ОШИБОК — код, исправляющий арифметические ошибки, код, предназначенный для контроля работы сумматора. При сложении чисел, представленных в двоичной системе счисления, одиночный сбой в работе сумматора приводит, как правило, к изменению результата на нек… … Математическая энциклопедия

Код Боуза — Коды Боуза Чоудхури Хоквингхема (БЧХ коды) в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с… … Википедия

Код Боуза-Чоудхури-Хоквингема — Коды Боуза Чоудхури Хоквингхема (БЧХ коды) в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с заранее… … Википедия

Код коррекции ошибок Рида-Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия

Код Рида-Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия

Источник

Помехоустойчивое кодирование для передачи цифрового телевидения по каналам связи

Владимир Блох
эксперт

Введение

При увеличении скорости передачи качество передачи оценивалось по BER – отношению количества ошибок по сравнению с количеством переданных бит. Появились понятия «готовность линии к передаче» и «качество передачи». Характеристики качества были приведены в рекомендациях G.811 и G.826 МСЭ-Т. При анализе характеристик качества период времени передачи исключается.

В XX веке появилось понятие «помехоустойчивое кодирование». Оно началось с появлением кодов Хэмминга, формулы и предела Шеннона.

Хотя, может быть, следует вспомнить Евклида, который 3500 лет назад ввел понятие помехоустойчивого кодирования. Определил необходимую скорость передачи символов и дистанцию между ними – «дистанция по Евклиду». Ею пользуются в США и сейчас, применяя TCM-модуляцию (теперь 8PSK – решетка с 8 состояниями), по правилу Унгербоека с пространственной избыточностью. Эффективность кодирования получается 3,6 дБ.

После 50-х годов прошлого века специалисты стали считать, что сбой импульсной посылки происходит не из-за игольчатого выброса шума в 5–10•10 6 пкВт, а из-за белого гауссового шума AWGN (Additive White Gaussian Noise) в канале с релеевскими замираниями.

Априорную вероятность ошибки определяли как:

отношение сигнал/шум на бит (SNR). При М-модуляции формулы имеют более сложный вид. Вероятность ошибки на бит – это вероятность того, что в сообщении из L битов m будут ошибочными.

учитывая, что ошибки при приеме кодовых символов происходят независимо с вероятностью po. При малой вероятности ошибки в канале с учетом скорости кода R = k/n можно считать:

Канальное кодирование позволяет исправлять ошибки цифровой информации за счет включения в поток избыточных импульсов. При этом уменьшается энергия одного бита. Она становится равной K/n.Eb.

Согласование возможности прохождения сигнала через радиотехнические цепи сделал Шеннон. Он предложил формулу, которая теперь носит его имя:

Шеннон показал, что пропускная способность канала C с аддитивным шумом AWGN является отношением средней мощности принимаемого сигнала S к средней мощности шума и ширине полосы пропускания W.

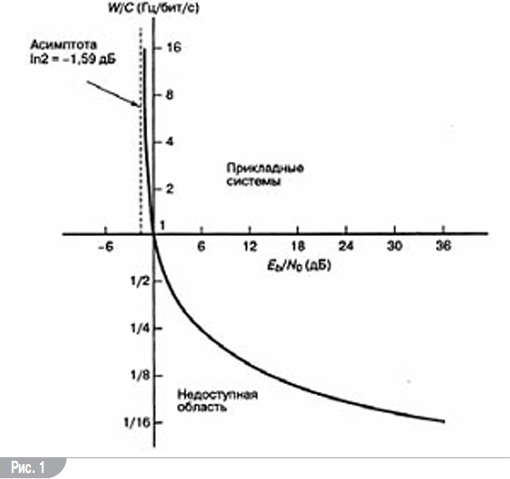
При увеличении спектра сигнала (с К8 на К32 в стандарте Т2) пропускная способность увеличивается. Пропускная способность имеет размерность бит/c. Нижнее предельное значение Eb/N0, при котором ни при какой скорости нельзя осуществить безошибочную передачу информации, называют пределом Шеннона, равным Eb/N0 = 1,6 дБ, где Eb – мощность сигнала на бит; N0 – полоса шума на бит.

На рис. 1 показана зависимость нормированной полосы канала от Eb и N0.

Телевизионный сигнал, выходящий со студии – аналоговый. Превращение его в цифровой осуществляется с помощью теоремы Котельникова. Она приводится в учебниках по телевидению. Поэтому не будем на ней останавливаться.

Первые помехоустойчивые коды предложил Хэмминг. Это были блочные коды, исправляющие одну ошибку. Они записывались так: К(n,k,d), где n число приходящих импульсов, к – информационных. Количество ошибок, которые может исправить код t = (d-1)/2.

Коды могут быть образованы с помощью примитивных полиномов или с помощью матрицы. Пример построения матриц для кода Хэмминга 5.3 приведен ниже.

Система помехоустойчивости состоит из:

Эффективность кодирования

Без кодирования энергия бита была равна Eb, а при блочном кодировании с учетом избыточности будет меньше на k/n. Следовательно, Ebk = k/nEb.

Скорость передачи канальных битов Rc должна превышать скорость передачи Rb в n/k раз.

Символьная передача Rs меньше канальной Rc в (log2M) раз.

Для систем с модуляцией и кодированием преобразование скорости имеет следующий вид:

Преобразование энергии битов в энергию символов связано такими же множителями, что и преобразователи скоростей. Отношение энергии канального бита к спектральной мощности шума Ec/No – это результат умножения Eb/No на коэффициент k/n. Путем умножения Ec/No на коэффициент (log2M) c вычисляется Pe.

Для систем, содержащих одновременно модуляцию и кодирование, преобразование отношения энергии к спектральной плотности мощности шума будет:

Отношение принимаемой мощности к спектральной плотности шума будет:

Синхронизация потока TS

Длительность полинома 1503 байта. Синхронное слово 0х47. Инвертированное синхронное слово 0хB8.

При модуляции QPSK и скорости внутреннего кода – 1/2 обеспечивается самая высокая защищенность при отношении сигнал/шум 3,1 дБ. При модуляции – 64QAM и скорости внутреннего кода 7/8 необходимо иметь соотношение сигнал/шум – 20,1 дБ.

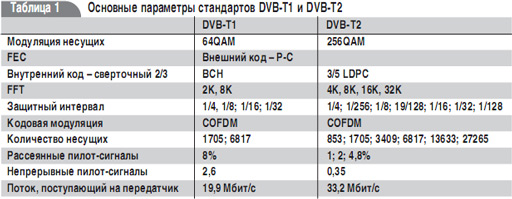
В табл. 1 приведены основные параметры двух стандартов.

Входной поток, поступающий на передатчик, подвергается сжатию по стандарту MPEG-2 или MPEG-4 и превращается в сигналы физического уровня PLPc, которые, расщепляясь, превращаются, в свою очередь, в потоки TS. Предложенная на рис. 1 система предполагает наличие трех составных потоков: SS.1; SS.2; SS.3 (каждый из них содержит кодирование по видео и звуку) и две субсистемы – SS.4 и SS.5. Все это через статистический мультиплексор (statistical multiplexer) объединяется и поступает на межсетевой переход (SS.2 Basic Gateway), затем с него расходятся на свои модуляторы. Потоки трансформируются в RF-каналы и т.д. и поступают на антенну. На приемной стороне потоки детектируются и демодулируются, потом поступают в телевизор.

В стандартах Т1и Т2 в качестве помехоустойчивого кода используется каскадный код Форни. В основе его построения лежит совместное использование двух кодов, состоящих из внешнего кода Рида – Соломона c коэффициентом кодирования R = K/N и внутреннего – сверточного r = k/n. Суммарный коэффициент кодирования равен rR = kK/nN. Причем закодированные символы внешнего кода кодируются кодом внутренним.

Минимальное расстояние каскадного кода D = d1d2, а кодовая скорость равна:

где r1r2 – кодовые скорости.

Коды Рида – Соломона

Коды Рида – Соломона (Р-С) с параметрами (n, k, d), где n = 2 S – 1, формируют один из n символов поля Галуа GF(2S) для каждой группы, содержащей последовательно информационные символы. Коды Р-С называют линейными кодами потому, что они образованы набором блоков фиксированной длины, в которых каждый элемент кодового слова выбирается из алфавита q-символов. Коды Р-С имеют максимально возможные минимальные кодовые расстояния, обеспечивающие наибольшую корректирующую способность по сравнению с другими линейными кодами. Код Р-С с m = m_o-1 характеризуется следующими параметрами:

Для детектирования кодов Р-С используют жесткое решение.

Чаще всего коды Р-С используют для передачи цифрового телевидения. При этом код Р-С имеет байтовую структуру, то есть S = 8, nmax = 256. Чаще всего используется код Р-С с параметрами: (204.188,16) или (204,188; t = 8). Полоса пропускания определяется символьной скоростью приходящего потока: Symbol Rate S:

Для 16QAM – m = 4, для 64QAM – 6, 256QAM – 8. Правка ошибок основывается на GHT = 0. Для определения вероятности ошибки при применении кода Рида – Соломона можно воспользоваться приведенной формулой.

Сверточные коды

Сверточные коды (СК) относятся к непрерывным кодам, где передаваемая последовательность не может быть разбита на независимые блоки. При СК дополнительные символы содержатся в последовательности предыдущих.

СК преобразует k0 информационных символов, поступающих на его вход, в n0 выходных кодовых символов, n0> k0. Выходные символы являются линейными комбинациями над полем GF(q) входных символов из предшествующих m блоков. Преимущество СК по отношению к блочным заключается в непрерывном обнаружении и исправлении ошибок. Сверточный код задается параметрами: n, k, К, где k – число входов; n – число выходов; r = k/n – кодовая скорость, K – конструктивная длина кода; ηa – длина кодового ограничения.

Параметрами СК-кода, характеризующими его помехоустойчивость, является минимальное свободное расстояние по Хэммингу между последовательностями сверточного кода по длине кодовых ограничений – deff. Оно определяет эффективность кода при разных значениях его скорости r. Об этом мы поговорим позднее.

Сверточные кодеры бывают несистематические, не имеющие обратных связей, и систематические, с обратными связями.

Выходные символы формируются с помощью рекуррентного соотношения из K информационных символов, поступающих в данный и предшествующие моменты времени. Величина K называется длиной кодового ограничения и играет ту же роль, что и длина блочного кода.

Способы декодирования сверточных кодов представлены.

Внешнее и внутреннее перемещение (3; 4; 5) для стандартов Т1 и Т2 рассмотрены в Л 2.5.

При COFDM-модуляции исходный спектр разделяется на N несущих частот ортогональных подканалов, в каждом из которых осуществляется модуляция последовательностью данных. В K = 8 используется от 64 до 6817 точек преобразования. Важным параметром систем является быстрое преобразование Фурье. Длительность преобразования Фурье составляет от 10 до нескольких сот мкс.

Для уменьшения влияния на приеме многолучевого распространения применяют защитный интервал, во время которого значение принятого символа не определяется. От 1/32 до 1/4 длительности быстрого преобразования Фурье для стандарта Т1.

Защитный интервал – это не просто пауза между полезными символами, достаточная для угасания сигнала символа до начала следующего. Он пропускает часть полезного сигнала, гарантирует сохранение ортогональности несущих принятого сигнала. Величина защитного интервала зависит от расстояния между передатчиками в одночастотных сетях или от задержки естественного эхо-сигнала в сетях вещания. Считают, что она должна содержать четвертую часть от величины полезного интервала.

В режиме OFDM каждый символ формируется одной поднесущей. В приемнике основные шаги процесса демодуляции выполняются в обратном порядке: полученные сигналы во временной области квантуются и поступают в процессор БПФ, который восстанавливает комплексный спектр. Затем спектральные компоненты обрабатываются как отдельные сигналы, для того чтобы декодировать данные, которые мультиплексируются в основной поток данных.

В передающем устройстве роль модулятора выполняет интегральная схема быстрого обратного преобразования Фурье.

В приемном устройстве – прямое преобразование Фурье и процессор, который восстанавливает комплексный спектр. Затем спектральные компоненты обрабатываются в отдельные сигналы для того, чтобы декодировать данные, которые мультиплексируются в основной поток телевидения.

Преобразование Фурье

Преобразование Фурье – это метод обработки, использующийся для анализа изменений сигнала во времени и выражения их в виде спектра.

Длительность преобразования Фурье:

Существенную экономию времени счета дает метод быстрого преобразования Фурье (БПФ), позволяющий сократить число рассчитываемых вариантов с N2 до Nlog2 N. Так, например, при N = 1024 экономия во времени составит около ста раз. Один из алгоритмов БПФ используется при передаче цифрового телевидения. В приемнике основные шаги процесса демодуляции выполняются в обратном порядке.

Основная задача стандарта DVB-T2 – передавать одновременно три программы цифрового телевидения высокой четкости. Поэтому там используют высокоскоростные помехоустойчивые коды.

Внешний код в стандарте Т2-БЧХ Боуза – Чоудхуда – Хоквингема

Этот код был известен и раньше. Применение его откладывалось из-за отсутствия элементной базы, работающей на высоких частотах.

Коды (БЧХ) представляют собой класс линейных циклических кодов, исправляющих кратные ошибки, и являются результатом обобщений кодов Хэмминга. Это обеспечивает свободу выбора длины блока, степени кодирования, размеры алфавита и возможности коррекции ошибок. В кодах БЧХ в случае больших n и кодовые слова записывают в начале последовательности. Например, кодовое слово (C_n-1,C_n-2,+…) в виде полинома C(x) = a(x)g(x). После ряда преобразований и умножения полинома на Xn-k получаем Xn-kb(x)=a(x)g(x)+p(x), где p(x) – полином. Степени не более n-k-1 определят ошибки передачи. Если он равен 0, то ошибок нет.

Коды БЧХ характеризуются следующими параметрами:

N = 2 m-1 ; r – любое; d = 2t + 1; t = (2m-1-k)/m/. Где m – целое положительное число, t – ошибки.

Величина энергетического выигрыша определяется rd (чем больше rd, тем больше выигрыш). БЧХ имеют параметры: n = 2 m – 1; n-k ≤ mt; dmin = 2t + 1.

Вероятности ошибки в кодовом блоке P, q-символе Ps и в бите Pb при декодировании БЧХ по максимуму правдоподобия приведены ниже:

Так как коды БЧХ относятся к циклическим блоковым кодам, задаваемым образующим полиномом, кодирование информационной последовательности осуществляется в соответствии с C(X) = U(X) g(x).

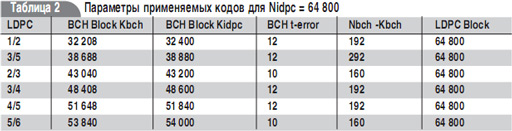
Применение в качестве внешнего кода BCH предложенной длины может исправлять от 10 до 12 ошибок. Двоичные коды БЧХ, порожденные примитивными полиномами поля Галуа GF(gm), меньше 210 могут исправлять несколько ошибок. Например, (255,9) – 63 ошибки. Предложенные в стандарте DVB-T2 длинные коды имеют в своем составе меньше избыточных битов, но при этом усложняется синдром исправления ошибок и увеличивается мощность на их передачу. В табл. 2 для стандарта DVB-T2 представлены параметры применяемых кодов для Nidpc = 64 800. Из них мы заключаем, что избыточность от всех представленных кодов одинакова.

Внутренний код LDPC (Low Density Parity Check codes) с низкой плотностью проверок. Код имеет минимальное расстояние d и поэтому все ошибки могут быть исправлены при почти линейной сложности алгоритма декодирования.

В работах показано, что LDPC-коды могут быть близки к пределу Шеннона. При скорости 1/2 с длиной блока 10000000 код отличается от предела Шеннона 0,0045 дБ.

Регулярный LDPC-код является линейным (n, k), проверочная матрица которого H имеет Хеммингов вес. Столбцы и строки равны J и K соответственно. Причем обе величины меньше длины кода N.

Применяя BCH + LDPC, удается получить выигрыш по сравнению с кодом Р-С + сверточный 5 дБ (рис. 4) DVB BlueBOOK A133. Применение модуляции несущих 256QAM увеличивает емкость канала на треть.

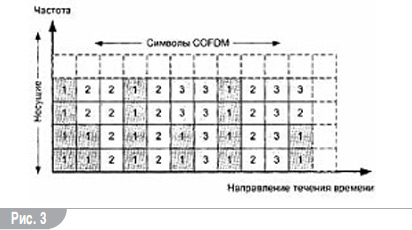
На вход системы поступают потоки от трех независимых программ телевидения высокой четкости (рис. 2). Эти потоки называются phsycal layer pipes (PLP). В DVB-T2 каждый из них помещается в свою PLP. Структура суперфрейма представлена на рис. 3. Программы поступают на передатчик последовательно.

Для одночастотных сетей введен режим MISO Multiple Input Single Output – много входов, один выход.

Количество пилот-сигналов уменьшено (табл. 1).

Источник