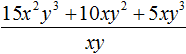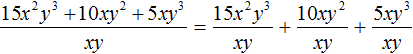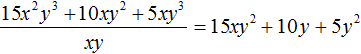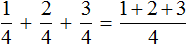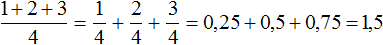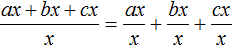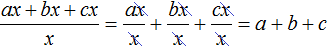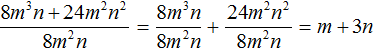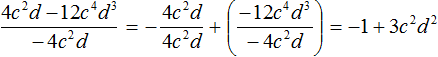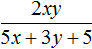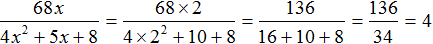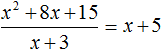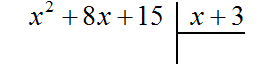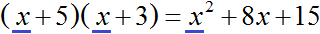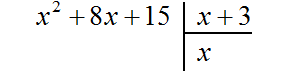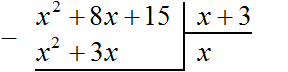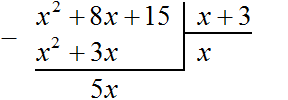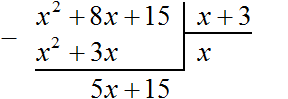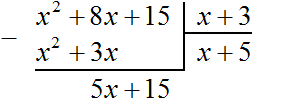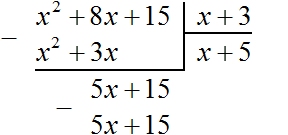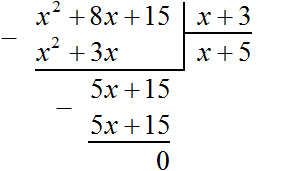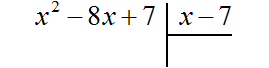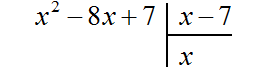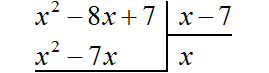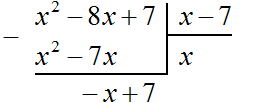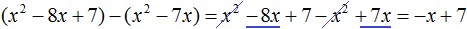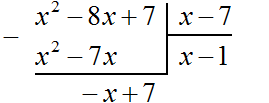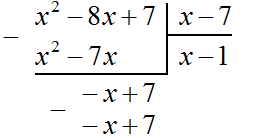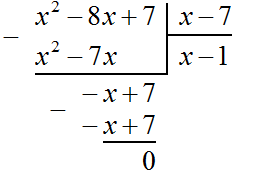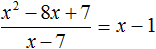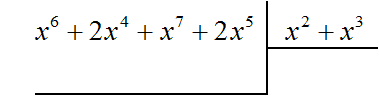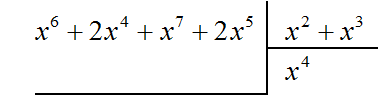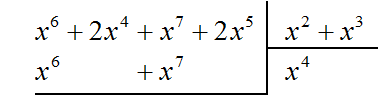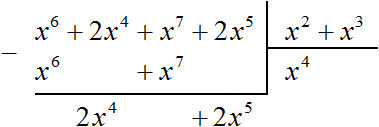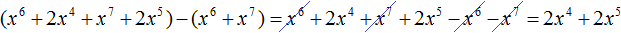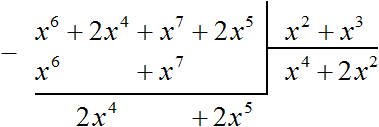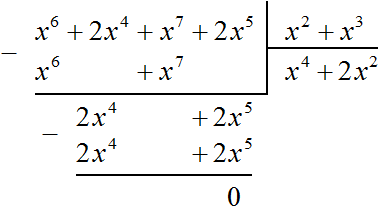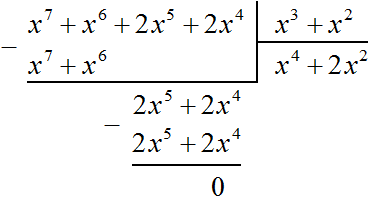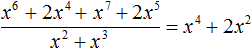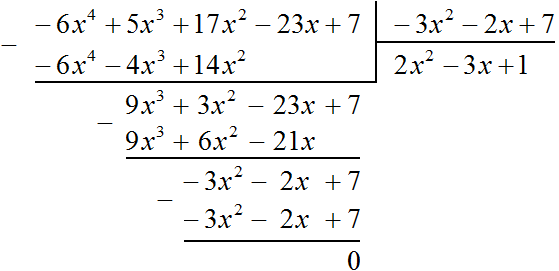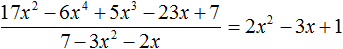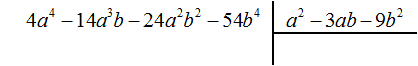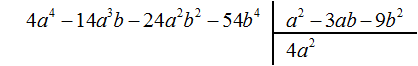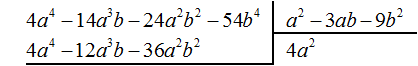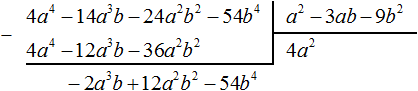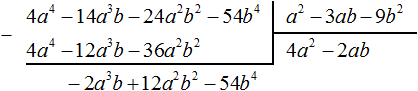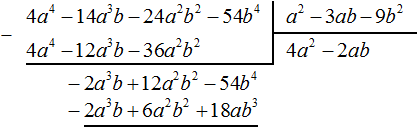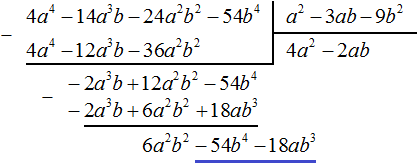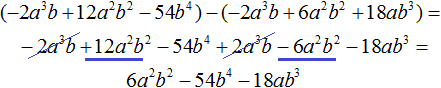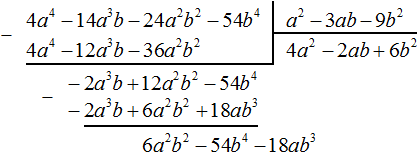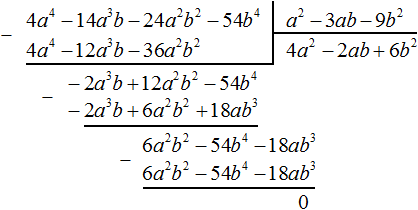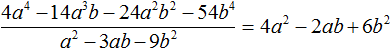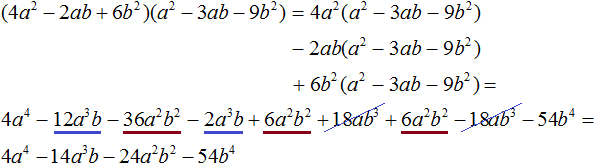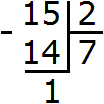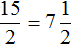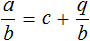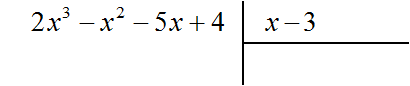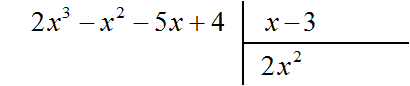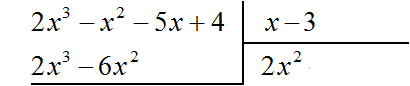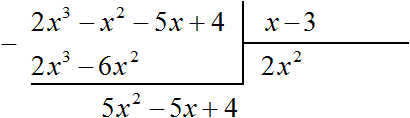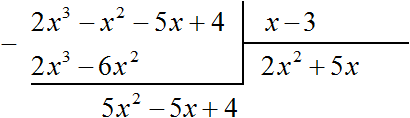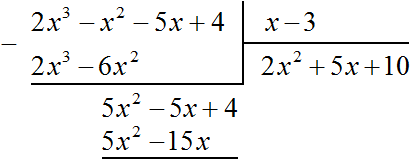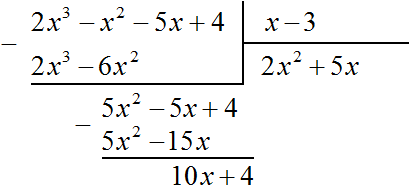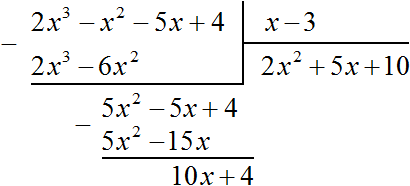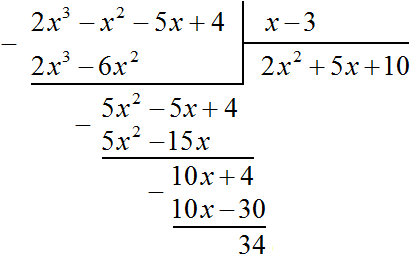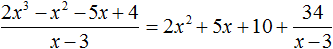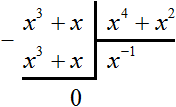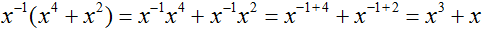деление многочленов в поле

Деление многочленов в полях

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Деление многочленов
Подскажите, как можно разделить многочлен p(x)=4^<4>+3^<3>+2^<2>+x-1 на.

Деление многочленов
Помогите пожалуйста люди, с делением полиномов ( + присутствует формула Евклида ), вот решить эти.

Деление многочленов с комплексными числами
Нужно поделить два многочлена: x2+x+1 на 2x+1. Если делить «уголком», в результате останется.

как другая то деление многочлена и запись не дробей а по модулю. в поле gf(5) например

Добавлено через 28 минут
попробую объяснить:
делим старшее слагаемое делимого на старшее слагаемое делителя
2x^6 / 5x^3
надо чтобы была не дробь 0.4 а по модулю поля в котором работаем например gf(7)
не могу врубить

Решение

Значит, я не понял вопрос.

Я же говорил про деление в поле многочленов по модулю некоторого неприводимого многочлена..

Образует ли система многочленов базис в линейном ространстве многочленов степени не выше 3
Образует ли система 1, t, t^2-t, t^3-t^2+t многочленов базис в линейном ространстве многочленов.

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Деление многочлена на многочлен (двучлен) столбиком (уголком)

С помощью данной математической программы вы можете поделить многочлены столбиком.
Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вам нужно или упростить многочлен или умножить многочлены, то для этого у нас есть отдельная программа Упрощение (умножение) многочлена

Немного теории.

Деление многочлена на многочлен (двучлен) столбиком (уголком)

В алгебре деление многочленов столбиком (уголком) — алгоритм деления многочлена f(x) на многочлен (двучлен) g(x), степень которого меньше или равна степени многочлена f(x).

Алгоритм деления многочлена на многочлен представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.

Для любых многочленов \( f(x) \) и \( g(x) \), \( g(x) \neq 0 \), существуют единственные полиномы \( q(x) \) и \( r(x) \), такие что
$$ \frac = q(x)+\frac $$
причем \( r(x) \) имеет более низкую степень, чем \( g(x) \).

Целью алгоритма деления многочленов в столбик (уголком) является нахождение частного \( q(x) \) и остатка \( r(x) \) для заданных делимого \( f(x) \) и ненулевого делителя \( g(x) \)

Пример

Разделим один многочлен на другой многочлен (двучлен) столбиком (уголком):
$$ \frac $$

6. Конец алгоритма.
Таким образом, многочлен \( q(x)=x^2-9x-27 \) — частное деления многочленов, а \( r(x)=-123 \) — остаток от деления многочленов.

Результат деления многочленов можно записать в виде двух равенств:
\( x^3-12x^2-42 = (x-3)(x^2-9x-27)-123 \)
или
$$ \frac = x^2-9x-27 + \frac<-123> $$

Источник

Деление многочленов

Продолжаем изучать многочлены. В данном уроке мы научимся их делить.

Деление многочлена на одночлен

Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.

Теперь делим каждый член многочлена 15x 2 y 3 + 10xy 2 + 5xy 3 на одночлен xy. Получающиеся частные будем складывать:

Получили привычное для нас деление одночленов. Выполним это деление:

При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.

Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.

Например, чтобы сложить дроби , и нужно записать следующее выражение:

Если мы вычислим выражение 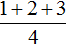, то получим дробь , значение которой равно 1,5.

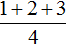
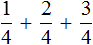
При этом выражение мы можем вернуть в исходное состояние , и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5

Вычисление каждой дроби даст в результате многочлен a + b + c

Пример 2. Разделить многочлен 8m 3 n + 24m 2 n 2 на одночлен 8m 2 n

Пример 3. Разделить многочлен 4c 2 d − 12c 4 d 3 на одночлен −4c 2 d

Деление одночлена на многочлен

Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.

Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.

Выражение 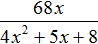представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования. Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:

Деление многочлена на многочлен

Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.

Деление многочлена на многочлен выполняется уголком. Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.

Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.

Сейчас наша задача найти первый член нового многочлена. Как это сделать?

Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.

Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.

Если первый член делимого (в нашем случае это x 2 ) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:

Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:

На этом деление завершено.

Пример 2. Разделить многочлен x 2 − 8x + 7 на многочлен x − 7

Записываем уголком данное деление:

Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:

Деление завершено. Таким образом, частное от деления многочлена x 2 − 8x + 7 на многочлен x − 7 равно x − 1

Пример 3. Разделить многочлен x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3

Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x 4

Вычитание многочлена 2x 4 + 2x 5 из многочлена 2x 4 + 2x 5 дало в результате 0, поэтому деление успешно завершилось.

В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.

Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.

Тогда деление уголком многочлена x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3 примет следующий вид:

Деление завершено. Таким образом, частное от деления многочлена x 6 + 2x 4 + x 7 + 2x 5 на многочлен x 2 + x 3 равно x 4 + 2x 2

При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.

Перепишем умножение (x 4 + 2x 2 )(x 2 + x 3 ) упорядочив члены многочленов в порядке убывания степеней.

Пример 4. Разделить многочлен 17x 2 − 6x 4 + 5x 3 − 23x + 7 на многочлен 7 − 3x 2 − 2x

Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:

Пример 5. Разделить многочлен 4a 4 − 14a 3 b − 24a 2 b 2 − 54b 4 на многочлен a 2 − 3ab − 9b 2

Умножим 4a 2 на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым:

Вычтем из делимого полученный многочлен 4a 4 − 12a 3 b − 36a 2 b 2

Умножим −2ab на делитель a 2 − 3ab − 9b 2 и полученный результат запишем под делимым −2a 3 b + 12a 2 b 2 − 54b 4

Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:

Деление многочлена на многочлен с остатком

Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.

Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:

То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:

Рациональное число читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.

Например, разделим многочлен 2x 3 − x 2 − 5x + 4 на многочлен x − 3

Умножим 2x 2 на делитель x − 3 и полученный результат запишем под делимым:

Вычтем из делимого полученный многочлен 2x 3 − 6x 2

Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x 2 − 5x + 4

Вычтем из многочлена 5x 2 − 5x + 4 многочлен 5x 2 − 15x

Поэтому при делении многочлена 2x 3 − 2x 2 − 5x + 4 на многочлен x − 3 получается 2x 2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:

Когда деление многочленов невозможно

Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.

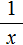
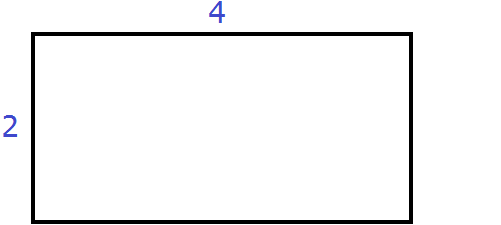
Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x − 1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x − 1 это дробь , которая не является произведением.

Пусть имеется прямоугольник со сторонами 4 и 2

Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.

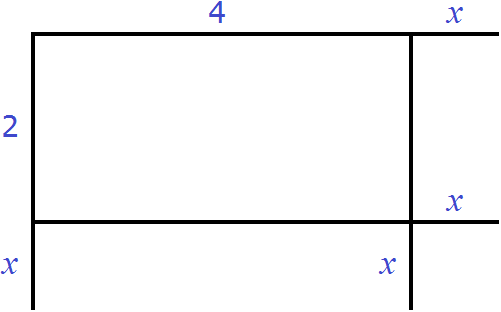
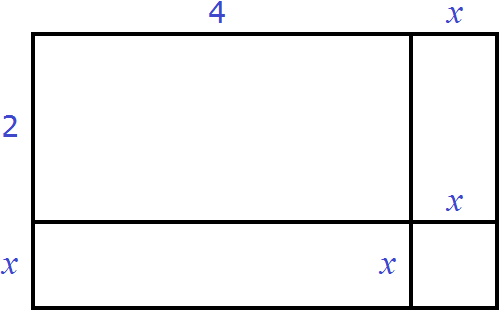
Увеличим длину и ширину этого прямоугольника на x

Достроим отсутствующие стороны:

Источник

Функциональная схема деления многочленов над GF(2)

В случае многочленов над GF(2) множитель h из соотношения (2.31) принимает вид:

Рекуррентные соотношения (2.33) позволяют синтезировать функциональную схему формирования остатка от деления многочленов над GF(2) на основе двух идеальных элементов: элемента задержки, обладающего памятью, и сумматора по модулю 2 (рисунок 2.1).

Пока мы рассматриваем идеальную схему. Поэтому будем считать смену состояний бесконечно быстрой, а переход всех элементов задержки в следующее устойчивое состояние одновременным.

Соединения Ь/, i = к-1, к- 2. О определяются коэффициентами делителя Ь <х).Если соответствующий коэффициент Ь <х)равен единице, то соединение будет присутствовать в схеме. И наоборот, соединение будет отсутствовать при равенстве коэффициента нулю. Поэтому соединения, соответствующие коэффициентам Ь(х), показаны на рисунке 2.1 пунктирными линиями.

В следующем устойчивом состоянии схемы, соответствующем первому этапу деления, значения с входов элементов задержки передаются на их выходы. Этот процесс соответствует суммированию к старших коэффициентов делимого а(х) и соответствующих коэффициентов делителя Ь(х), умноженных на старший коэффициент делимого а_п. При этом происходит укорочение делимого на один разряд, а в элемент задержки с_т-к+^ загружается следующий коэффициент делимого -а_п

Таким образом, для получения остатка от деления многочлена а(лг) над GF(2) на многочлен Ь(х) над GF(2) коэффициенты делимого а(х) просто должны быть последовательно загружены в схему, общий вид которой определяется рисунком

Поскольку коэффициенты остатка соответствуют коэффициентам с,(х) при i =

как коэффициенты Ск-1, Ск-2. Со многочлена с_п-/с+i(x) соответственно.

Пример 2.3.1. Рассмотрим применение схемы аппаратного деления многочленов для формирования проверочной последовательности циклического кода длины п = 15 с порождающим многочленом g(x) = х 5 + х 4 + х 2 + 1 (длина информационной последовательности к = 10). К этому коду мы еще вернемся позднее, в главе 4 (см. пример 4.1.1).

Функциональная схема деления на образующий многочлен, соответствующая этому случаю, показана на рисунке 2.2.

1 а’ 4 + 1 а 13 + 1 а’ 2 + 0 а»+ 0 х 10 + 0 а 9 + 0 а 8 + 1 х + 0а 6 + 1 а 5 + 0а 4 + 0а 3 + 0а 2 + 0а+ 0

Так как а_п = 1, то на первом этапе выполняется суммирование первых пяти коэффициентов делимого с последовательностью коэффициентов порождающего многочлена g(x). После этого производится сдвиг последовательности на один элемент, и схема переходит в первое устойчивое состояние, в котором элементы задержки хранят первые пять битов первого результирующего многочлена Ci(x) (последовательность С4С3С2С1С0 = 01101, таблица 2.3).

На втором этапе деления старший коэффициент многочлена ci(x), полученного на предыдущем этапе, равен нулю. Поэтому коэффициенты результирующего многочлена предыдущего этапа, загруженные в элементы задержки, суммируются с последовательностью нулевых значений. Затем последовательность коэффициентов, как обычно, укорачивается путем сдвига на один символ (бит).

Видно, что на каждом этапе деления старший коэффициент многочлена, полученного на предыдущем этапе, либо обнуляется при суммировании со старшим коэффициентом, имеющим единичное значение, либо уже имеет нулевое значение. Таким образом, в вычислении значения старшего коэффициента результирующего многочлена каждого этапа, по сути, нет необходимости, так как это значение всегда равно нулю. Поэтому на каждом этапе выполняется сдвиг исходной последовательности и место старшего коэффициента текущего многочлена с,(х) занимает старший коэффициент укороченного многочлена c, + i(x).

Основу аппаратной реализации рассмотренной функциональной схемы деления многочленов над полем составляют устройства цифровой логики из семейства триггеров.

Источник