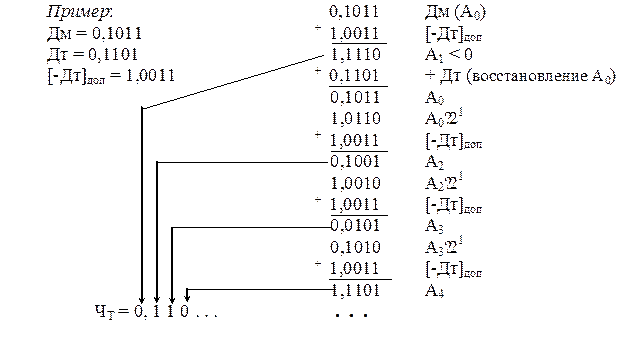деление в прямом коде
Деление чисел в прямых кодах.
Алгоритм деления с восстановлением остатка состоит в следующем.
Из этого следует, что восстанавливать остаток не обязательно. Достаточно сдвинуть полученный отрицательный остаток влево на один разряд и добавить делитель. Это является основой алгоритма для выполнения деления без восстановления остатка.
Алгоритм деления без восстановления остатка.
1. Выполняется пробное вычитание с формированием первого остатка A1=[Дм]доп+[-Дм]доп. Далее, если А1 k не выполняется равенство pk=r ∙ pk-1, то системы принято называть взвешенными. Количество разрядов m должно удовлетворять выражению m ≥ log2r. Если десятичное число записано в виде (4), то будем говорить, что число представлено в двоично-десятичном коде. Наибольшее распространение из них получили коды, в которых десятичная цифра представляется двоичной тетрадой (BCD коды). Существует множество способов кодирования десятичных цифр. Существенным при этом является простота представления инверсных кодов и простота выделения (формирования) сигнала переноса из цифры в цифру.
Сформулируем набор требований, позволяющих упростить выполнение арифметических операций и операций перевода чисел.
§ Четность, состоит в том, что четным десятичным цифрам соответствуют только четные двоичные коды, либо наоборот, что обеспечивает эффективность операций округления, умножения и деления чисел в BCD кодах.
§ Дополнительность, заключается в том, что сумма двоичного кода и инверсного ему кода любой десятичной цифры должна быть равна 9. Это обеспечивает эффективность операции алгебраического сложения в BCD кодах.
§ Упорядоченность, то есть большей десятичной цифре соответствует большая тетрада, и наоборот.
§ Единственность представления десятичной цифры двоичной тетрадой.
§ Взвешенность, то есть каждому разряду двоичного представления десятичной цифры поставлен в соответствие вес. Это обеспечивает эффективность всех арифметических и логических операций в BCD кодах.
Если каждая десятичная цифра кодируется соответствующим двоичным эквивалентом, то такое кодирование называется кодом прямого замещения.

Основной недостаток этого кода заключается в том, что инверсия какой либо цифры оказывается цифрой, дополняющей данную цифру до 15, а не до 9.
a = 0100



В табл. 4 показаны различные способы кодирования десятичных цифр.
9. Деление в прямых кодах.
Деление осуществляется следующим образом.
Определяется знак частного путем сложения по модулю два знаков делимого и делителя. Затем производится собственно деление. При этом цифры частного определяются последовательно, разряд за разрядом, начиная со старшего разряда, путем вычитания, например, сдвинутого на один разряд вправо делителя из остатка, полученного от предыдущего вычитания. При определении первой цифры частного, за остаток принимается все делимое со знаком плюс. После каждого вычитания делитель сдвигается вправо на один разряд по отношению к делимому и образующимся остаткам. Если остаток от вычитания положительный или равен нулю, то в соответствующий разряд частного заносится 1. Если остаток отрицательный, то соответствующая цифра частного равна О. Для того, чтобы получить следующую после нуля цифру частного, можно из последнего положительного остатка вычесть делитель, дополнительно сдвинутый на один разряд вправо. Однако в этом случае необходимо выполнить дополнительную операцию сложения для восстановления последнего положительного остатка.
8 Метод пропуска такта суммирования
Данный метод применим к любой схеме выполнения операции умножения. Сущность его заключается в том, что если очередной анализируемый разряд множителя равен нулю, то такт суммирования пропускается и без задержки на время суммирования Ts вырабатывается устройством управления очередной сигнал сдвига, обеспечивающий сдвиг на один разряд множителя и накопленной суммы частичных произведений или множимого в зависимости от схемы умножения. Если принять, что в двоичном коде множителя в любом разряде с равной вероятностью может находиться как 0, так и 1, то среднее кол-во тактов суммирования при перемножении двух n разрядных чисел сокращается вдвое
Метод расшифровки и одновременного умножения на два разряда множителя
Очевидно, что в последнем случае старший член правой части 100 представляет собой единицу младшего разряда следующей анализируемой пары разрядов множителя. Для пояснения описанного метода рассмотрим пример выполнения операции умножения при анализе одновременно двух разрядов множителя. Пусть множимое [X]пр = 0,11110101, а
множитель [Y]пр = 0,100001101. Будем считать, что множимое может передаваться в сумматор со сдвигом на один разряд влево. Тогда для исключения переполнения разрядной сетки сумматора добавим в него перед знаковыми разрядами один дополнительный разряд, а для округления результата добавим в сумматор еще один младший дополнительный разряд. Сложение будем производить в модифицированном обратном коде. Полагаем, что в сумматоре возможен сдвиг за один такт на два разряда вправо. С учетом сделанных оговорок последовательность действий в сумматоре можно представить следующим образом.
В соответствии с поставленной выше задачей выполнения операции умножения одновременно на два разряда множителя представим операнды в следующем виде: |X|=11110101; |Y|=y8 y7 y6 y5 y4 y3 y2 y1 = 10001101. Схема реализации операции ускоренного умножения представлена ниже. Легко проверить, что результат умножения сомножителей X и Y по обычной схеме дает аналогичный результат, то есть Z=X*Y = 0,10000111.
Деление чисел с фиксированной запятой в прямом и дополнительном кодах
Деление чисел с фиксированной запятой имеет ряд особенностей по сравнению с умножением. Главная из них заключается в том, что частное определяется по одному разряду за каждый цикл вычисления, а общее количество разрядов частного и, следовательно, циклов вычислений определяется, как правило, необходимой точностью, которая зависит как от точности исходных данных, так и от применяемых форматов чисел в конкретной ЭВМ.
В наиболее распространенных в настоящее время ЭВМ с системой команд X86 или IA-32 деление производится над числами с фиксированной точкой со знаком или без знака форматом байт или слово. При этом результат получается в виде целой части и остатка, причем каждая часть результата занимает фиксированное число байт.
Очевидно, что такой подход не может быть использован при делении чисел с фиксированной запятой, так как он предполагает, что, в общем случае, частное имеет целую часть, большую нуля, а это противоречит определению формата числа с фиксированной запятой. Для чисел, заданных в таком формате, будем исходить из следующих общих условий, не связанных со структурой конкретной ЭВМ:
Эти положения позволяют адаптировать предлагаемые алгоритмы деления к ЭВМ с произвольной архитектурой, в том числе, длине слова.
Деление чисел, заданных в прямом коде
Рассмотрим варианты деления чисел для случая, когда делимое и делитель представлены в прямом коде. При любом алгоритме деления в прямом коде чисел с фиксированной запятой результат, в общем случае, получается
При любом алгоритме деления в прямом коде чисел с фиксированной запятой результат, формируется поразрядно и так же, как и операнды, в прямом коде. Из этого следует, что в общем случае он формируется «с недостатком», так как какая-то дальнейшая цифра после прекращения выполнения операции может оказаться равной единице, тем самым увеличивая полученный результат. Это свойство может быть использовано для текущей проверки получаемых в ходе вычислений значений.
Деление со сдвигом и автоматическим восстановлением остатка
На первом этапе проводится определение знака частного:
Затем сравниваем абсолютные величины делимого и делителя.
Если α0 ≥ 0, то |X| ≥ |Y|. Следовательно, для чисел с фиксированной запятой Z = ∞, и дальнейшее деление не имеет смысла.
Деление чисел в прямых кодах
Машинные методы деления
§ с восстановлением остатков;
§ без восстановления остатков.
Независимо от метода деления после каждого вычитания делителя формируется цифра частного. Операция деления является операцией, дающей не всегда точный результат. Поэтому признаком окончания операции деления
может быть достижение заданной точности (по числу сдвиговых сигналов). Если при выполнении деления получен нулевой i-й остаток, то деление прекращается и в оставшиеся разряды частного записываются нули. Первым шагом деления двух чисел машиной является пробное вычитание, выявляющее соотношение между делимым и делителем. При делении в случае переполнения следует: для чисел с фиксированной запятой процесс остановить, с плавающей запятой продолжить до конца, а потом, после получения последней n-й цифры частного, число сдвигается вправо на один разряд с добавлением единицы к порядку, равному разности порядков делимого и делителя.
Алгоритм деления с восстановлением остатка состоит в следующем.
1. Выполняется пробное вычитание с формированием первого остатка A1=[Дм]доп+[-Дт]доп. Далее, если А1
1) необходимо затрачивать время на восстановление остатка;
2) процесс деления нерегулярный, в зависимости от делимого и делителя
частное будет содержать нулей больше или меньше, и чем больше нулей, тем больше требуется времени на восстановление остатков.
Рассмотрим пример деления чисел.
Как видно из примера, для получения остатка Аi+2 необходимо выполнить
Из этого следует, что восстанавливать остаток необязательно. Достаточно сдвинуть полученный отрицательный остаток влево на один разряд и добавить делитель. Это является основой алгоритма для выполнения деления без восстановления остатка.
Алгоритм деления без восстановления остатка.
1. Выполняется пробное вычитание с формированием первого остатка A1=[Дм]доп+[-Дт]доп. Далее, если А1
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
К вопросу о делении
Нам подвернулась возможность провести небольшое, но крайне интересное тактическое учение
В процессе исследований нового МК от известной фирмы на основе архитектуры Cortex-М4 (я об этом обязательно еще напишу) возник вопрос, насколько быстро может работать операция целочисленного деления в аппаратной реализации. Натурный эксперимент дал несколько неожиданный результат: деление 32-разрядного числа на 32-разрядное выполняется за 3 такта частоты процессора — ну ни фига ж себе, как быстро. Выяснилось, что это имеет место только с определенными операндами, но дальнейшие исследования показали, что никогда время выполнения деления не превосходит 7 тактов. Полученные результаты вызвали легкую оторопь («и это не некая фигура речи, которая неизвестно что означает, а вполне конкретный глагол» — Дивов, как всегда, бесподобен).
Ну нельзя же просто так взять и быстро поделить такие длинные числа, странно как то, но факты — упрямая вещь. Представил себе картину, что вызывает меня завтра к себе Президент РФ и ставит передо мной задачу сделать МК не хуже, чем у ARM (согласен, что картина бредовая, но чего на свете не бывает), а я растеряно на него гляжу и понимаю, что не смогу сделать такое деление таких чисел за такое время, и не оправдаю ожиданий, на меня возлагаемых (ну на самом то деле я всегда смогу втихую купить лицензию у ARM, и сделать вид, будто бы придумал все сам, многие так и делают, но от меня то ВВП ждет совсем другого, да и потом — его то я обмануть смогу, а вот себя вряд ли).
И стало мне грустно, что в ARM сидят ребята намного умнее меня, и пошел я с тоской во взоре подглядеть в Инете, как они это делают. На сайте ARM никакой информации по времени исполнения не нашел, в одном из материалов по STM32 было указано, что деление занимает от 2 до 7 тактов, что соответствует наблюдениям, но информации о том, как это делается, нет.
В общем, Инет всемогущий особо не помог, есть трюки с делением на константу, сам о них писал в одном из постов, но у нас иная ситуация, есть алгоритм Ньютона и ускоренная его версия, но это явно не по делу, есть алгоритм на основе преобразования Фурье, но это для очень больших чисел и вряд ли выполнится за 7 тактов даже на архитектуре ARM. Пришлось придумывать самому и решение было найдено, причем настолько простое и очевидное, что становится несколько неловко от того, что это не было сделано мгновенно после формулировки задачи.
Прежде, чем смотреть мое решение, предлагаю Вам найти свое самостоятельно, а потом сравните с моим, и, если они отличаются то жду Вас в комментариях.
Итак, как нам быстро (не более, чем за 7 тактов) поделить два 32-разрядных числа с получением 32-разрядного результата.
Для начала вспомним, как вообще осуществляется деление в двоичной арифметике в
классической форме. Алгоритм достаточно прост и понятен — вычитаем делитель из делимого. Если результат неотрицателен (делим без-знаковые числа), то очередной разряд результата делаем равным единице и результат рассматриваем, как следующее делимое, в противном случае очередной бит результата равен 0. Перед следующим тактом уменьшаем делитель в два раза (либо сдвигаем его вправо, либо сдвигаем влево делимое) и уменьшаем вес бита в 2 раза (аналогичными сдвигами). Таким образом, мы получаем за один такт один бит результата и вся операция продлится 32 такта. В этом процессе есть еще начальный сдвиг, но на оценку ситуации в целом он не влияет. Будем ускорять, но как?
Обратим внимание, что полученный алгоритм сильно напоминает работу АЦП с последовательным приближением и вспоминаем, что есть и другой метод преобразования, намного более быстрый — параллельное преобразование. А что, если…
Будем вычитать из делителя не только делимое, но и делимое*2 и делимое*3 (одновременно, на трех сумматорах), тогда мы получим три бита (знаки результатов) информации, которые принимают 4 различных значения, значит из них можно извлечь сразу 2 бита результата. Далее экстраполируем подобный подход для 3,4,5 бит результата.
Чтобы получить 5 бит информации за один такт, нам потребуется 31 сумматор, на каждом из которых будет выполняться операция Делимое-Делитель*н(1-31), знаки результата пропускаем через шифратор и получаем сразу 5 бит результата. Затем сдвигаем делимое на 5 разрядов влево и повторяем до готовности. Тогда нам потребуется 32/5=6.4=>7 тактов для полного завершения операции.
Так что задача поделить за 7 тактов решена, остается вопрос – как можно ли сократить данное время, ведь в исследуемом МК оно бывает меньше 7. Напрашивающееся решение — на этапе подготовки алгоритма определить номер старшего значащего разряда делимого (Ч) и делителя (З) и сразу станет ясно, сколько старших битов частного равны нулю, так что мы можем пропустить первую либо несколько фаз алгоритма. Например, если Ч