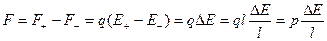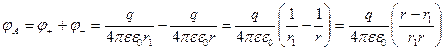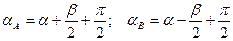диполь в неоднородном электрическом поле
3.2. Электрический диполь
Чтобы понять механизм поведения диэлектриков в поле на микроскопическом уровне, нам надо сначала объяснить, как может электрически нейтральная система реагировать на внешнее электрическое поле. Простейший случай — полное отсутствие зарядов — нас не интересует. Мы знаем наверняка, что в диэлектрике имеются электрические заряды — в составе атомов, молекул, ионов кристаллической решетки и т. д. Поэтому мы рассмотрим следующую по простоте конструкции электронейтральную систему — два равных по величине и противоположных по знаку точечных заряда +q и –q, находящихся на расстоянии l друг от друга. Такая система называется электрическим диполем.
Электрический диполь — это система, состоящая из двух точечных равных по величине и противоположных по знаку зарядов, находящихся на расстоянии l друг от друга (рис. 3.6).
Рис. 3.6. Электрический диполь
Линии напряженности электрического поля и эквипотенциальные поверхности электрического диполя выглядят следующим образом (рис. 3.7, 3.8, 3.9)
Рис. 3.7. Линии напряженности электрического поля электрического диполя
Рис. 3.8. Эквипотенциальные поверхности электрического диполя
Рис. 3.9. Линии напряженности электрического поля и эквипотенциальные поверхности
Основной характеристикой диполя является электрический дипольный момент. Введем вектор l, направленный от отрицательного заряда (–q) к положительному (+q), тогда вектор р, называемый электрическим моментом диполя или просто дипольным моментом, определяется как
Рассмотрим поведение «жесткого» диполя — то есть расстояние 
Рис. 3.10. Силы, действующие на электрический диполь, помещенный во внешнее поле
Пусть направление дипольного момента составляет с вектором Е угол 
Так как ql = р, то М = рЕ sin 
(Напомним, что символ
означает векторное произведение векторов а и b.) Таким образом, при неизменном дипольном моменте молекулы (
Под действием момента сил М диполь поворачивается, при этом совершается работа
которая идет на увеличение его потенциальной энергии. Отсюда получаем потенциальную энергию диполя в электрическом поле
если положить const = 0.
Из рисунка видно, что внешнее электрическое поле стремится повернуть диполь таким образом, чтобы вектор его электрического момента р совпал по направлению с вектором Е. В этом случае 




На рис. 3.11 показан опыт, иллюстрирующий возникновение момента электрических сил, действующих на диэлектрик в электрическом поле. На удлиненный диэлектрический образец, расположенный под некоторым углом к силовым линиям электростатического поля, действует момент сил, стремящийся развернуть этот образец вдоль поля. Диэлектрическая палочка, подвешенная за середину внутри плоского конденсатора, разворачивается перпендикулярно его пластинам после подачи на них высокого напряжения от электростатической машины. Появление вращающего момента обусловлено взаимодействием поляризовавшейся палочки с электрическим полем конденсатора.
Рис. 3.11. Момент электрических сил, действующих на диэлектрик в электрическом поле
В случае неоднородного поля на рассматриваемый диполь будет действовать еще и равнодействующая сила Fpaвн, стремящаяся его сдвинуть. Мы рассмотрим здесь частный случай. Направим ось х вдоль поля Е. Пусть диполь под действием поля уже повернулся вдоль силовой линии, так что отрицательный заряд находится в точке с координатой x, а положительный заряд расположен в точке с координатой х + l. Представим себе, что величина напряженности поля зависит от координаты х. Тогда равнодействующая сила Fpaвн равна
Такой же результат может быть получен из общего соотношения
где энергия П определена в (3.8). Если Е увеличивается с ростом x, то
и проекция 
Рассмотрим несколько опытов, иллюстрирующих возникновение силы, действующей на диэлектрик, помещенный в неоднородное электрическое поле.
На рис. 3.12 показано втягивание диэлектрика в пространство между обкладками плоского конденсатора. В неоднородном электростатическом поле на диэлектрик действуют силы, втягивающие его в область более сильного поля.
Рис. 3.12. Втягивание жидкого диэлектрика в плоский конденсатор
Это демонстрируется при помощи прозрачного сосуда, в который помещен плоский конденсатор, и налито некоторое количество жидкого диэлектрика — керосина (рис.3.13). Конденсатор присоединен к высоковольтному источнику питания — электростатической машине. При ее работе на нижнем краю конденсатора, в области неоднородного поля, на керосин действует сила, втягивающая его в пространство между пластинами. Поэтому уровень керосина внутри конденсатора устанавливается выше, чем снаружи. После выключения поля уровень керосина между пластинами падает до его уровня в сосуде.
Рис. 3.13. Втягивание керосина в пространство между обкладками плоского конденсатора
В реальных веществах нечасто встречаются диполи, образованные только двумя зарядами. Обычно мы имеем дело с более сложными системами. Но понятие электрического дипольного момента применимо и к системам со многими зарядами. В этом случае дипольный момент определяется как
где 


Пусть наша система зарядов электрически нейтральна. В ней есть положительные заряды, величины которых и местоположения мы обозначим индексом «+». Индексом «–» мы снабдим абсолютные величины отрицательных зарядов и их радиус-векторы. Тогда выражение (3.10) может быть записано в виде
В (3.11) в первом слагаемом суммирование ведется по всем положительным зарядам, а во втором — по всем отрицательным зарядам системы.
Электрическая нейтральность системы означает равенство полного положительного заряда и суммы абсолютных величин всех отрицательных зарядов
Введем теперь понятие «центр зарядов» — положительных R + и отрицательных R –
Выражения (3.13) аналогичны формулам для центра масс в механике, и потому мы назвали их центрами положительных и отрицательных зарядов, соответственно. С этими обозначениями и с учетом соотношения (3.12) мы записываем электрический дипольный момент (3.11) системы зарядов в виде
где l-вектор, проведенный из центра отрицательных зарядов в центр положительных зарядов. Смысл нашего упражнения заключается в демонстрации, что любую электрически нейтральную систему зарядов можно представить как некий эквивалентный диполь.
Дополнительная информация
Диполь в неоднородном электрическом поле



Диполь в однородном электрическом поле.
На каждый из зарядов диполя действуют силы: 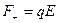
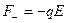
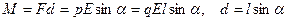
М – вращающий момент F – силы, действующие на диполь
d – плечо сил l – плечо диполя
p – дипольный момент E – напряжённость
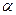
Под действием вращающего момента, диполь повернётся и установится по направлению линий напряжённости. Векторы p и Е будут параллельны и однонаправлены.
Диполь в неоднородном электрическом поле.
Вращающий момент есть, значит диполь повернётся. Но силы будут неравны, и диполь будет двигаться туда, где сила больше.
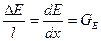
Собственное поле диполя.
Но 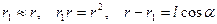
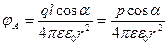
Пусть диполь находится в точке О, а его плечо мало. Тогда:
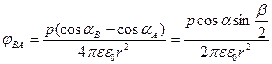
Формула получена с учётом:
Таким образом разность потенциалов зависит от синуса половинного угла, под которым видны точки диполя, и проекции дипольного момента на прямую, соединяющие эти точки.
Диполь в неоднородном внешнем электрическом поле
Если диполь помещен в неоднородное внешнее электрическое поле, то силы, действующие на заряды q+ и q—, не равны по величине и направлению, так как напряженность электрического поля в точках расположения зарядов не одинакова по величине, отличается на величину

В этом случае на отрицательный заряд действует сила

На положительный заряд действует сила

Результирующая сила, действующая на диполь,




Такое же действие оказывает электрическое поле на молекулы диэлектрика.
3.2. Свободные и связанные (поляризационные) заряды
в диэлектриках. Поляризация диэлектриков.
Вектор поляризации (поляризованность)

Различные вещества поляризуются по-разному в зависимости от их строения. Наиболее часто встречаются следующие виды поляризации диэлектриков:
а) деформационная поляризация – это поляризация диэлектриков, при которой у атомов возникает (индуцируется) дипольный момент за счет деформации электронных орбит. Наблюдается у диэлектриков, состоящих из неполярных молекул у веществ, молекулы которых имеют симметричное строение (N2, H2, O2, CO2, CH4);
б) ориентационная, или дипольная поляризация, которая заключается в ориентации имеющихся дипольных моментов молекул по направлению электрического поля. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрического поля и теплового движения) возникает преимущественная ориентация дипольных моментов по полю. Ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура. Она характерна для диэлектриков, состоящих из полярных молекул веществ, молекулы которых имеют асимметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов не совпадают. К таким веществам, например, относятся H2O, NH3, SO2, CO;
При помещении диэлектрика во внешнее электрическое поле он поляризуется, т.е. приобретает отличный от нуля электрический дипольный момент:

где pi – дипольный момент одной молекулы.
Для количественной характеристики поляризации диэлектриков вводится в рассмотрение физическая величина, численно равная электрическому дипольному моменту единицы объема диэлектрика:

Эта величина называется вектором поляризации, или поляризованностью. Если поле или диэлектрик однородны, то вектор поляризации одинаков по всему объему. Такую поляризацию называют однородной. Если эти условия не выполняются, то поляризацию называют неоднородной.
У большинства диэлектриков, кроме так называемых сегнетоэлектриков, вектор поляризации пропорционален напряженности внешнего электрического поля:

где c – диэлектрическая восприимчивость вещества, не зависящая от напряженности внешнего электрического поля.
Между вектором поляризации P и поверхностной плотностью связанных зарядов s ‘ имеется связь

т. е. поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации в данной точке поверхности диэлектрика.




где 
Внутри диэлектрика в этом случае существует результирующее электрическое поле с напряженностью

где 


Вне диэлектрика напряженность внешнего поля равна напряженности результирующего электрического поля.
Так как поле перпендикулярно граням пластины и плоскостям, то En = E, а с учетом того, что 

Из формулы (3.16) имеем



Следовательно, относительная диэлектрическая проницаемость среды показывает, во сколько раз электрическое поле ослабевает за счет диэлектрика.
Индукция электрического поля D внутри диэлектрика и вне диэлектрика одинакова, т.к. при умножении 


где D = ee0E– индукция (электрическое смещение) электрического поля внутри диэлектрика;
Do = e0E – индукция (электрическое смещение) электрического поля вне диэлектрика.
Таким образом, индукция электрического поля в диэлектрике изменяет свое направление, но не изменяет свою величину, в то время как напряженность электрического поля E ¹ Eo. Полученный результат справедлив для любых электрических полей.
Следовательно, на границе раздела двух сред происходит изменение вектора напряженности электрического поля E (уменьшается число силовых линий вектора E), а вектор индукции электрического поля не изменяется (изменяется лишь вид силовых линий вектора D). Отсюда вывод: поток вектора индукции электрического поля через любую замкнутую поверхность остается величиной постоянной.
Для потока вектора индукции электрического поля D справедлива теорема Остроградского-Гаусса: поток вектора индукции электрического поля через любую замкнутую поверхность равен алгебраической сумме электрических зарядов, заключенных внутри этой замкнутой поверхности.
Математически эту теорему можно записать так: