для чего нужен бинарный код
Двоичный код — где и как применяется?
Сегодня я по-особому рад своей встрече с вами, дорогие мои читатели, ведь я чувствую себя учителем, который на самом первом уроке начинает знакомить класс с буквами и цифрами. А поскольку мы живем в мире цифровых технологий, то я расскажу вам, что такое двоичный код, являющийся их основой.
Начнем с терминологии и выясним, что означит двоичный. Для пояснения вернемся к привычному нам исчислению, которое называется «десятичным». То есть, мы используем 10 знаков-цифр, которые дают возможность удобно оперировать различными числами и вести соответствующую запись.
Следуя этой логике, двоичная система предусматривает использование только двух знаков. В нашем случае, это всего лишь «0» (ноль) и «1» единица. И здесь я хочу вас предупредить, что гипотетически на их месте могли бы быть и другие условные обозначения, но именно такие значения, обозначающие отсутствие (0, пусто) и наличие сигнала (1 или «палочка»), помогут нам в дальнейшем уяснить структуру двоичного кода.
Зачем нужен двоичный код?
До появления ЭВМ использовались различные автоматические системы, принцип работы которых основан на получении сигнала. Срабатывает датчик, цепь замыкается и включается определенное устройство. Нет тока в сигнальной цепи – нет и срабатывания. Именно электронные устройства позволили добиться прогресса в обработке информации, представленной наличием или отсутствием напряжения в цепи.
Дальнейшее их усложнение привело к появлению первых процессоров, которые так же выполняли свою работу, обрабатывая уже сигнал, состоящий из импульсов, чередующихся определенным образом. Мы сейчас не будем вникать в программные подробности, но для нас важно следующее: электронные устройства оказались способными различать заданную последовательность поступающих сигналов. Конечно, можно и так описать условную комбинацию: «есть сигнал»; «нет сигнала»; «есть сигнал»; «есть сигнал». Даже можно упростить запись: «есть»; «нет»; «есть»; «есть».
Но намного проще обозначить наличие сигнала единицей «1», а его отсутствие – нулем «0». Тогда мы вместо всего этого сможем использовать простой и лаконичный двоичный код: 1011.
Безусловно, процессорная техника шагнула далеко вперед и сейчас чипы способны воспринимать не просто последовательность сигналов, а целые программы, записанные определенными командами, состоящими из отдельных символов.
Но для их записи используется все тот же двоичный код, состоящий из нулей и единиц, соответствующий наличию или отсутствию сигнала. Есть он, или его нет – без разницы. Для чипа любой из этих вариантов – это единичная частичка информации, которая получила название «бит» (bit — официальная единица измерения).
Условно, символ можно закодировать последовательностью из нескольких знаков. Двумя сигналами (или их отсутствием) можно описать всего четыре варианта: 00; 01;10; 11. Такой способ кодирования называется двухбитным. Но он может быть и:
Скажу честно, единой официальной версии нет, то так сложилось, что именно комбинация из восьми знаков стала стандартной мерой хранящейся информации, именуемой «байт». Таковая могла применяться даже к одной букве, записанной 8-и битным двоичным кодом. Итак, дорогие мои друзья, запомните пожалуйста (если кто не знал):
Так принято. Хотя символ, записанный 2-х или 32-х битным значением так же номинально можно назвать байтом. Кстати, благодаря двоичному коду мы можем оценивать объемы файлов, измеряемые в байтах и скорость передачи информации и интернета (бит в секунду).
Бинарная кодировка в действии
Для стандартизации записи информации для компьютеров было разработано несколько кодировочных систем, одна из которых ASCII, базирующаяся на 8-и битной записи, получила широкое распространение. Значения в ней распределены особым образом:
Расшифровка значений в ней показано в таблице.
Если вы считаете, что «0» и «1» расположены в хаотичном порядке, то глубоко ошибаетесь. На примере любого числа я вам покажу закономерность и научу читать цифры, записанные двоичным кодом. Но для этого примем некоторые условности:
Теперь, мои любознательные друзья, вы не только знаете что такое двоичный код, но и умеете преобразовать зашифрованную им информацию.
Язык, понятный современной технике
Конечно, алгоритм считывания двоичного кода процессорными устройствами намного сложнее. Но зато его помощью можно записать все что угодно:
Помимо этого, благодаря простоте «изложения» возможны различные способы записи бинарной информации:
Дополняет преимущества двоичного кодирования практически неограниченные возможности по передаче информации на любые расстояния. Именно такой способ связи используется с космическими кораблями и искусственными спутниками.
Так что, сегодня двоичная система счисления является языком, понятным большинству используемых нами электронных устройств. И что самое интересное, никакой другой альтернативы для него пока не предвидится.
Думаю, что изложенной мною информации для начала вам будет вполне достаточно. А дальше, если возникнет такая потребность, каждый сможет углубиться в самостоятельное изучение этой темы.
Я же буду прощаться и после небольшого перерыва подготовлю для вас новую статью моего блога, на какую-нибудь интересную тему.
Двоичная система счисления
Все что-то слышали о двоичной системе счисления, все знают, что это некий «язык компьютеров». Но почему именно так? Почему не пользоваться привычной десятичной системой? В чем, собственно, смысл?
Что такое двоичная система? Это позиционная система счисления с основанием 2. Вот только цифры «два» в ней нет, есть только 0 и 1, и так как цифры две, система называется двоичной (бинарной).
Современный цифровой язык, это ноли и единицы, больше ничего и не нужно. Самое интересное, так называемый машинный код использовался людьми задолго до появления самих машин, а, возможно, даже по появления чисел.
Зачем нужна двоичная система
Двоичная, или бинарная система счисления удобна своей простотой. С помощью комбинации нолей и единиц можно записать любой число и любую букву, что угодно может быть закодировано таким образом.
Но главное, что значения всего два. Это либо «ноль», либо «единица». Сигнал либо есть, либо его нет, свет горит или не горит, есть отверстие или нет (перфокарта), намагничен сектор или размагничен… Аналогии можно приводить бесконечно. Главное, что кодировать сигнал просто. Не нужно создавать сложные механизмы или устройства, достаточно только двух состояний.
Например, еще до того как люди научились считать и писать, сигналы передавались с помощью дыма от костра или ударов в барабаны.
Бинарная система — это просто, ничего проще просто нет. Есть, конечно, и древнейшая унитарная система, где значение всего одно (например, только 1) но с ее помощью нельзя ничего закодировать.
В любой микросхеме транзистор может прибывать в двух положениях «закрыто» или «открыто» (0 или 1) ток пропускается или нет.
Кстати, азбука Морзе — это тоже двоичный код (точка или тире), так же, как и древнейшая сигнальная система — «оптический телеграф». Это это просто огонь костра, который можно закрыть и открыть (огонь есть, или огня нет) ночью, а днем так же использовать дым.
Да, двоичная система используется потому, что с ее помощью удобно кодировать информацию, нужны всего 2 значения. Но удобно ли это считать?
Как считать
Как использовать двоичную систему для записи чисел? Так же как и десятичную. Самым простым примером можно считать кодовый замок, такой как на чемоданах. Каждый диск которого, вращается и может принимать значение от 0 до 9. Достаточно представить, что вместо десяти цифр есть только 2, ноль и единица.
Так как система позиционная, это будет выглядит так:
Сейчас здесь записано число «ноль». Чтобы получилась единица, нужно провернуть крайний правый диск один раз.
Начинается самое интересное, как будет выглядеть число «два»? Крутим правое колесико… И снова получаем 0, ведь других значений нет. Нужно поступить так же, как и в десятичной системе, перенести разряд влево. Только в десятичной, это происходит когда значение превышает 9, а в двоичной сразу после 1.
| Двоичная система | Десятичная система |
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
Сто в двоичной системе — это 1100100.
Очень интересно в бинарной системе выглядит таблица умножения:
Легко запомнить, неправда ли? 0*0=0, 0*1=0, 1*1=1… И все!
Все математические операции выполняются точно так же
Если сложит в столбик то получается нагляднее
100
Складываем ноли, получаем 0, складываем две единицы, получаем ноль (2 раза провернули диск) и единичку переносим вправо.
Как видите, математика та же, вот только запись чисел неудобная, слишком много нолей и единиц, для человека — неудобно, машине же все равно.
Так же как с цифрами можно поступить с буквами. Латинская буква «a» будет выглядеть как 01001010 кириллическая «а» — 000011100010111000011001, и даже пробел — 00010100.
История создания
Ясно, что человечество пользовалось двоичным кодом очень давно. И сигнальные системы с дымом от костров и даже китайская Книга Перемен (700 лет до нашей эры) с ее гексаграммами известны очень давно. Но окончательно практический смысл бинарный код получил совсем недавно (если не считать азбуку Морзе).
Великий Лейбниц занимался двоичной системой в 17 веке, но применить бинарную систему счисления было особо негде. В том же Веке Паскаль создал свою счетную машину (суммирующую), использующую десятичную систему. Оказалось, что считать на таком «калькуляторе» не так уж и удобно.
Суммирующая машина Паскаля (десятичная)
И только в 40-х годах 20 веке, вместе с появлением первых электронный вычислительных машин двоичный код явил всю свою безусловную полезность и красоту. Именно как машинный язык. Записывать информацию в котором гораздо проще, чем привычными нам средствами, буквами и цифрами.
То же самое, в двоичном коде можно сделать проще
Для чего нужна двоичная система счисления сегодня, мы прекрасно знаем, у каждого в кармане есть смартфон. На самом деле, ноли и единицы используются намного чаще, чем десятичная система, даже если мы, люди, этого и не видим. Не удивительно, мы использовали двоичную систему на протяжении всей истории, но до эры машин даже не замечали этого.
Значение двоичного кода – почему компьютеры работают с единицами и нулями
Компьютеры не понимают слов и цифр так, как это делают люди. Современное программное обеспечение позволяет конечному пользователю игнорировать это, но на самых низких уровнях ваш компьютер оперирует двоичным электрическим сигналом, который имеет только два состояния: есть ток или нет тока. Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате.
Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять. Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.
Подсчет в двоичном формате
В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.
1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)
Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.
Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.
Почему компьютеры используют двоичные файлы
Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.
Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.
Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый, транзистор для выполнения расчетов с двоичным кодом.
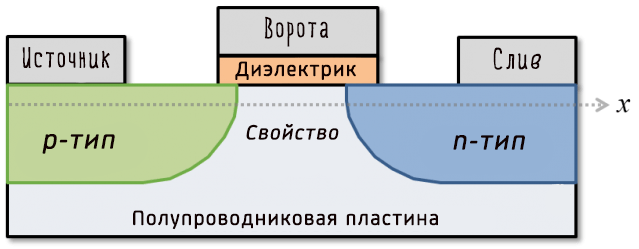
Вот схема типичного транзистора:
По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным странностям квантовой механики).
Почему только двоичная система
Поэтому вы можете подумать: «Почему только 0 и 1? Почему бы не добавить ещё одну цифру?». Хотя отчасти это связано с традициями создания компьютеров, вместе с тем, добавление ещё одной цифры означало бы необходимость выделять ещё одно состояние тока, а не только «выключен» или «включен».
Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное аппаратное обеспечение, способное на это, не жизнеспособно как замена двоичных вычислений. Например, существует, так называемый, тройной компьютер, разработанный в 1950-х годах, но разработка на том и прекратилась. Тернарная логика более эффективна, чем двоичная, но пока ещё нет эффективной замены бинарного транзистора или, по крайней мере, нет транзистора столь же крошечных масштабов, что и двоичные.
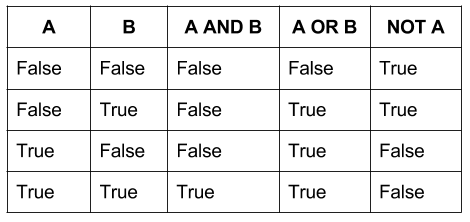
Причина, по которой мы не можем использовать тройную логику, сводится к тому, как транзисторы соединяются в компьютере и как они используются для математических вычислений. Транзистор получает информацию на два входа, выполняет операцию и возвращает результат на один выход.
Бинарная таблица истинности, работающая на двоичной логике, будет иметь четыре возможных выхода для каждой фундаментальной операции. Но, поскольку тройные ворота используют три входа, тройная таблица истинности имела бы 9 или более. В то время как бинарная система имеет 16 возможных операторов (2^2^2), троичная система имела бы 19683 (3^3^3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.
Кто знает? В будущем мы вполне возможно увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации. Пока же мир будет продолжать работать в двоичном режиме.
Что такое двоичный код
Задача сегодняшней публикации – разобраться в том, что такое двоичный код, для каких целей и где используется двоичный код и зачем вообще он нужен.
Двоичный код – это система обозначений из двух элементов, различные комбинации которых служат для представления (кодировки) информации.
В качестве элементов системы наиболее часто выступают цифры «0» и «1». Но в действительности обозначения могут быть произвольными, исходя из характера сведений, которые требуется кодировать.
Главное – чтобы соответствующие элементы обозначали взаимоисключающие либо противоположные по значению данные.
Великолепным примером двоичного кода могут служить любые пары антонимов, к примеру, «да/нет», «белое/черное», «включено/выключено» и т.д.
Для описания двоичного кода используется понятие разряда (более точно – двоичного разряда), объединяющего целочисленную группу элементов двоичного кода.
Например, в системе, использующей базовые элементы 0 и 1, два двоичных разряда могут быть представлены следующими четырьмя комбинациями: 00, 01, 10 и 11.
Три двоичных разряда могут иметь следующий вид: 000, 001, 010, 011, 100, 101, 110 и 111.
Число двоичных разрядов может быть сколь угодно большим в зависимости от характера решаемых задач и объема кодируемой информации.
Форма представления данных с помощью двоичных разрядов характерна для позиционного двоичного кода, лежащего в основе двоичной системы счисления, применяемой сплошь и рядом во всех типах вычислительной техники.
Увеличение разрядности на единицу приведет к удвоению числа комбинаций в позиционном двоичном коде.
При двух символах (смотри примеры выше) мы имеем 4 комбинации, при трех – 8 комбинаций, при четырех – 16 комбинаций, при n символах – 2 n комбинаций.
С помощью двух символов можно закодировать практически любую информацию. Доказательством тому служат современные компьютеры, работа которых невозможна без такой кодировки.
Характерная особенность систем счисления, использующих разрядный двоичный код, заключается в возможности обозначения одного и того же числа различной комбинацией символов, отличающихся между собой по разрядности.
Например, в двоичной системе счисления единицу можно представить по-разному: 1, 01, 001, 0001 и т.д.
Нумерация двоичных разрядов осуществляется справа налево.
Если взять двоичный код 01011, то первый разряд будет иметь значение 1, второй разряд – 1, третий разряд – 0, четвертый – 1 и пятый разряд – 0:
Примеры двоичного кода
С помощью трех двоичных разрядов можно обозначить восемь десятичных чисел от 0 до 7:
0 = 000
1 = 001
2 = 010
3 = 011
4 = 100
5 = 101
6 = 110
7 = 111
Эта таблица отражает перевод десятичных чисел в двоичный код.
Поскольку число двоичных разрядов ничем не ограничено, с помощью такой кодировки можно зашифровать любое привычное нам десятичное число.
111 → 1 * 2 2 + 1 * 2 1 + 1 * 2 0 = 4 + 2 + 1 = 7
101 → 1 * 2 2 + 0 * 2 1 + 1 * 2 0 = 4 + 0 + 1 = 5
Зачем нужен двоичный код
Основное назначение двоичного кода – шифрование и кодирование информации.
Его главные преимущества – минимальное число символов, используемых для кодирования информации, и удобство – с машинной точки зрения – оперирования зашифрованными с их помощью данными.
Допустим, нам необходимо закодировать фразу «ХОЛОДНОЕ ЛЕТО».
Установим произвольные соответствия букв двоичному коду: Х – 000, О – 001, Л – 010, Д – 011, Н – 100, Е – 101, Т – 111.
Фото 2. Двоичный код лежит в основе двоичной системы счисления
Тогда закодированная фраза примет следующий вид: 000001010001011100001101010101111001 (36 символов).
Если получатель зашифрованного кода знает, что в основе кодировки каждой буквы лежат три двоичных разряда, то расшифровать фразу ему не составит никакого труда.
В данном случае мы имеем дело с однозначно декодируемым кодом (то есть код может быть расшифрован одним единственным способом).
Для сокращения длины кода может применяться неравномерный двоичный код.
Тогда кодировщик сознательно отступает от принципа разрядности, присваивая буквам произвольное число разрядов.
Например, если Х будет иметь обозначение 01, О – 00, Л – 100, Д – 101, Н – 110, Е – 111, Т – 1111, то фразе «ХОЛОДНОЕ ЛЕТО» будет соответствовать строка 01001000010111000111100111111100 (32 символа).
В данной фразе будет однозначно декодироваться фрагмент «ХОЛОДНО», после чего дешифровщику придется ломать голову над выбором приемлемой трактовки кода: «Е ЛЕТО», «Е ЛЕЕЛ», «Е ЛТЕО», «ТОЕЕЛ» и т.д.
Данный пример указывает на проблемы с использованием непродуманных комбинаций двоичного кода.
При правильном же подборе кодов неравномерный двоичный код позволяет не только сократить объем передаваемого сообщения, но и начать его дешифровку после поступления уже первых нескольких символов, не дожидаясь пока сообщение будет получено в полном объеме.
Виды двоичных кодов
Представление в памяти компьютера целочисленных значений производится с помощью беззнакового двоичного кода, основанного на представлении двоичных разрядов степенями двойки.
К примеру, для шестнадцатиразрядного кода допустимыми будут значения чисел от 0 до 65535.
На практике приходится решать задачи посложнее.
Фото 3. С помощью двоичного кода можно закодировать все что угодно
Машине или компьютеру достаточно трудно объяснить разницу между положительными и отрицательными числами. Отдельного представления требуют и числа с плавающей запятой, дробные или трансцендентные числа.
Инженеры придумали способ, как обходить эти проблемы, не выходя за пределы использования двоичного кода. Для решения озвученных проблем используется знаковый двоичный код.
В частности, для определения знака числа используется старший разряд в слове.
Если слово начинается с символа «0», значит число положительное (имеет знак «+»), если с символа «1», значит оно – отрицательное (имеет знак «-»).
Недостаток знакового двоичного кода кроется в необходимости раздельной обработки цифрового и знакового разрядов, что заставляет разработчиков программного обеспечения прибегать к усложненным алгоритмам обработки данных.
Как следствие, программный код увеличивается в объеме, а скорость его работы замедляется.
Видео о двоичном коде: