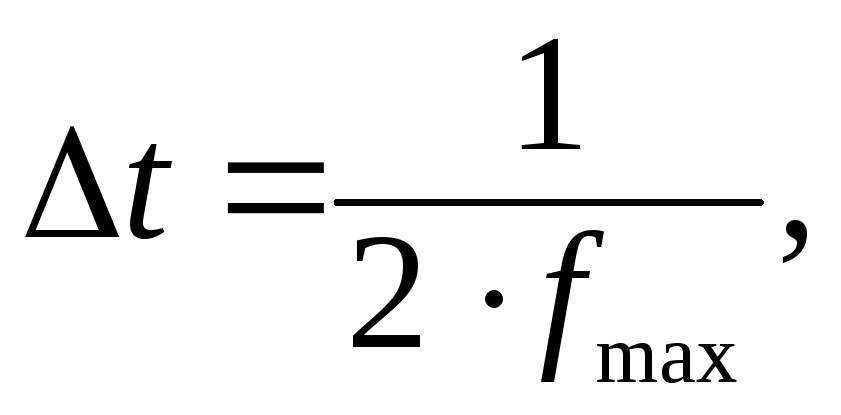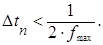для чего нужна избыточность в коде
2.2. Избыточность кодов.
Понятие избыточности означает, что фактическая энтропия кода или сообщения (Н) меньше, чем максимально возможная энтропия (Hmax), т. е. число символов в сообщении или элементов в символе кода больше, чем это требовалось бы при полном их использовании.
Понятие избыточности легко пояснить следующим примером.
Выделение полезного сигнала на уровне помех — одна из основных проблем передачи информации. Одним из путей повышения надёжности передачи сообщений может быть передача дополнительных символов, т.е. повышение избыточности сообщений.
Действительно, по теореме Котельникова (§ 1.7), непрерывное сообщение (сигнал) можно передать последовательностью мгновенных отсчетов его значений с промежутками между ними 
где fmax – верхняя граничная частота в спектре сигнала.
При наличии помех промежутки между отсчетами (Δtn) необходимо уменьшать, т.е.
В этом случае мы увеличиваем число отсчетов и, следовательно, увеличиваем избыточность сообщения и тем самым повышаем его помехозащищенность.
Пусть сообщение из n символов содержит количество информации I. Если сообщение обладает избыточностью, то его (при отсутствии шума) можно передать меньшим числом символов n0 (n0 n .
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Избыточность кодов.
Понятие избыточности означает, что фактическая энтропия кода или сообщения (Н) меньше, чем максимально возможная энтропия (Hmax), т. е. число символов в сообщении или элементов в символе кода больше, чем это требовалось бы при полном их использовании.
Понятие избыточности легко пояснить следующим примером.
Выделение полезного сигнала на уровне помех — одна из основных проблем передачи информации. Одним из путей повышения надёжности передачи сообщений может быть передача дополнительных символов, т.е. повышение избыточности сообщений.
Действительно, по теореме Котельникова (§ 1.7), непрерывное сообщение (сигнал) можно передать последовательностью мгновенных отсчетов его значений с промежутками между ними 
где fmax – верхняя граничная частота в спектре сигнала.
При наличии помех промежутки между отсчетами (Δtn) необходимо уменьшать, т.е.
В этом случае мы увеличиваем число отсчетов и, следовательно, увеличиваем избыточность сообщения и тем самым повышаем его помехозащищенность.
Пусть сообщение из n символов содержит количество информации I. Если сообщение обладает избыточностью, то его (при отсутствии шума) можно передать меньшим числом символов n0 (n0
Дата добавления: 2017-05-18 ; просмотров: 4277 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Избыточное кодирование, код Хэмминга
Избыточное кодирование (англ. redundant encoding) — вид кодирования, использующий избыточное количество информации с целью последующего контроля целостности данных при записи/воспроизведении информации или при её передаче по линиям связи.
| Определение: |
| Код определяет [math]d[/math] ошибок, если при передаче кодового слова, в котором [math]\leq d[/math] ошибок, алгоритм декодирования скажет, что есть ошибка. |
| Определение: |
| Код исправляет [math]d[/math] ошибок, если при передаче кодового слова, в котором [math]\leq d[/math] ошибок, алгоритм декодирования сможет восстановить исходное слово. |
Содержание
Код, определяющий одну ошибку [ править ]
Кодирование Хэмминга [ править ]
| [math]a[/math] | [math]b[/math] | [math]a \oplus b[/math] |
|---|---|---|
| [math]c[/math] | [math]d[/math] | [math]c \oplus d[/math] |
| [math]a \oplus c[/math] | [math] b \oplus d [/math] |
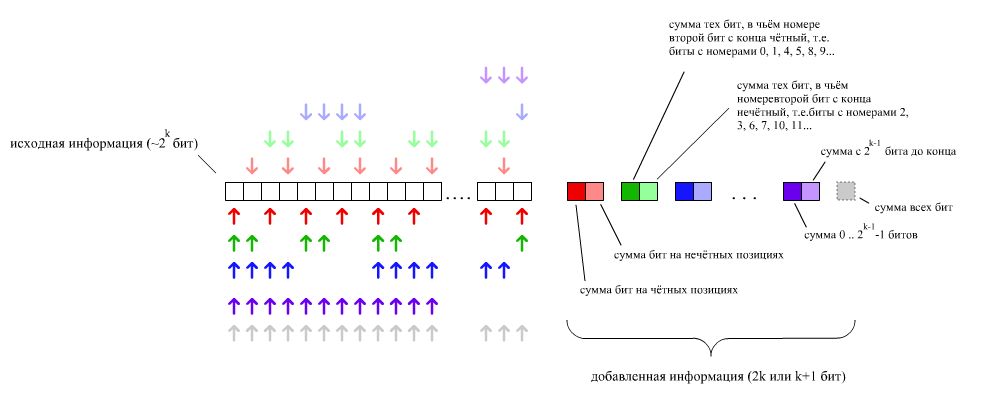
По аналогичному принципу можно закодировать любое число бит. Пусть мы имеем исходную строку длиной в [math]2^k[/math] бит. Для получения её кода добавим к ней [math]k[/math] пар бит по следующему принципу:
Теперь заметим, что в случае наличия ошибки в исходной строке, ровно один бит в каждой паре будет равен единице. Тогда можно оставить только один бит из пары. Однако этого будет недостаточно, поскольку если только один добавленный бит не соответствует строке, то нельзя понять, ошибка в нём или в строке. На этот случай можно добавить ещё один контрольный бит — [math] \mathrm X \mathrm O \mathrm R[/math] всех битов строки.
Определение и устранение ошибок в общем случае [ править ]
Пусть [math]\Sigma[/math] — исходный алфавит, [math]C: \Sigma \to B^m[/math] — кодирование, [math]B=(0,1)[/math]
[math]d: B^m \times B^m \to \mathbb
Определим [math]d_0 = \min[/math] [math]
Тогда легко понять, что код, полученный преобразованием [math]C[/math] может исправлять [math]
Коды избыточности: простыми словами о том, как надёжно и дёшево хранить данные
Так выглядит избыточность
Коды избыточности* широко применяются в компьютерных системах для увеличения надёжности хранения данных. В Яндексе их используют в очень многих проектах. Например, применение кодов избыточности вместо репликации в нашем внутреннем объектном хранилище экономит миллионы без снижения надёжности. Но несмотря на широкое распространение, понятное описание того, как работают коды избыточности, встречается очень редко. Желающие разобраться сталкиваются примерно со следующим (из Википедии):
Меня зовут Вадим, в Яндексе я занимаюсь разработкой внутреннего объектного хранилища MDS. В этой статье я простыми словами опишу теоретические основы кодов избыточности (кодов Рида — Соломона и LRC). Расскажу, как это работает, без сложной математики и редких терминов. В конце приведу примеры использования кодов избыточности в Яндексе.
Ряд математических деталей я не буду рассматривать подробно, но дам ссылки для тех, кто хочет погрузиться глубже. Также замечу, что некоторые математические определения могут быть не строгими, так как статья рассчитана не на математиков, а на инженеров, желающих разобраться в сути вопроса.
* Под термином «коды избыточности» в статье подразумевается инженерный термин «erasure codes».
1. Суть кодов избыточности
Суть всех кодов избыточности предельно простая: хранить (или передавать) данные так, чтобы они не пропадали при возникновении ошибок (поломках дисков, ошибках передачи данных и т. д.).
В большинстве* кодов избыточности данные разбиваются на n блоков данных, для них считается m блоков кодов избыточности, всего получается n + m блоков. Коды избыточности строятся таким образом, чтобы можно было восстановить n блоков данных, используя только часть из n + m блоков. Далее мы рассмотрим только блочные коды избыточности, то есть такие, в которых данные разбиваются на блоки.
Чтобы восстановить все n блоков данных, нужно иметь минимум n из n + m блоков, так как нельзя получить n блоков, имея только n-1 блок (в этом случае пришлось бы 1 блок брать «из воздуха»). Достаточно ли n произвольных блоков из n + m блоков для восстановления всех данных? Это зависит от типа кодов избыточности, например коды Рида — Соломона позволяют восстановить все данные с помощью произвольных n блоков, а коды избыточности LRC — не всегда.
Хранение данных
В системах хранения данных, как правило, каждый из блоков данных и блоков кодов избыточности записывается на отдельный диск. Тогда при поломке произвольного диска исходные данные все равно можно будет восстановить и прочитать. Данные можно будет восстановить даже при одновременной поломке нескольких дисков.
Передача данных
Коды избыточности можно использовать для надёжной передачи данных в ненадёжной сети. Передаваемые данные разбивают на блоки, для них считают коды избыточности. По сети передаются и блоки данных, и блоки кодов избыточности. При возникновении ошибок в произвольных блоках (вплоть до некоторого количества блоков), данные все равно можно безошибочно передать по сети. Коды Рида — Соломона, например, используют для передачи данных по оптическим линиям связи и в спутниковой связи.
* Есть также коды избыточности, в которых данные не разбиваются на блоки, например коды Хэмминга и коды CRC, широко применяемые для передачи данных в сетях Ethernet. Это коды для помехоустойчивого кодирования, они предназначены для обнаружения ошибок, а не для их исправления (код Хэмминга также позволяет частично исправлять ошибки).
2. Коды Рида — Соломона
Коды Рида — Соломона — одни из наиболее широко распространённых кодов избыточности, изобретённые ещё в 1960-х и впервые получившие широкое применение в 1980-х для серийного выпуска компакт-дисков.
Ключевых вопросов для понимания кодов Рида — Соломона два: 1) как создавать блоки кодов избыточности; 2) как восстанавливать данные с помощью блоков кодов избыточности. Найдем на них ответы.
Для упрощения далее будем считать, что n=6 и m=4. Другие схемы рассматриваются по аналогии.
Как создавать блоки кодов избыточности
Каждый блок кодов избыточности считается независимо от остальных. Для подсчёта каждого блока используются все n блоков данных. На схеме ниже X1-X6 — блоки данных, P1–P4 — блоки кодов избыточности.
Все блоки данных должны быть одинакового размера, для выравнивания можно использовать нулевые биты. Полученные блоки кодов избыточности будут иметь тот же размер, что и блоки данных. Все блоки данных разбиваются на слова (например, по 16 бит). Допустим, мы разбили блоки данных на k слов. Тогда все блоки кодов избыточности тоже будут разбиты на k слов.
Для подсчёта i-го слова каждого блока избыточности будут использоваться i-е слова всех блоков данных. Они будут считаться по следующей формуле:
Зачем нужны поля Галуа
Казалось бы, всё просто: разбиваем данные на блоки, блоки — на слова, с помощью слов блоков данных считаем слова блоков кодов избыточности — получаем блоки кодов избыточности. В целом это так и работает, но дьявол в деталях:
Эти проблемы не позволяют использовать для кодов Рида — Соломона целые числа. Решение проблемы оригинальное, его можно описать следующим образом: давайте придумаем специальные числа, которые можно представить с помощью слов нужной длины (например, 16 бит), и результат выполнения всех операций над которыми (сложение, вычитание, умножение, деление) также будет представлен в памяти компьютера при помощи слов нужной длины.
Такие «специальные» числа давно изучает математика, их называют полями. Поле — это множество элементов с определёнными для них операциями сложения, вычитания, умножения и деления.
Таким образом, мы имеем систему уравнений, с помощью которых можно построить блоки кодов избыточности, написав соответствующую компьютерную программу. С помощью этой же системы уравнений можно выполнить восстановление данных.
* Это не строгое определение, скорее описание.
Как восстанавливать данные
Восстановление нужно тогда, когда из n + m блоков часть блоков отсутствует. Это могут быть как блоки данных, так и блоки кодов избыточности. Отсутствие блоков данных и/или блоков кодов избыточности будет означать, что в уравнениях выше неизвестны соответствующие переменные x и/или p.
Уравнения для кодов Рида — Соломона можно рассматривать как систему уравнений, в которых все значения альфа, бета, гамма, дельта — константы, все x и p, соответствующие доступным блокам, — известные переменные, а остальные x и p — неизвестные.
Например, пусть блоки данных 1, 2, 3 и блок кодов избыточности 2 недоступны, тогда для i-й группы слов будет следующая система уравнений (неизвестные отмечены красным):
Мы имеем систему из 4 уравнений с 4 неизвестными, значит можем решить её и восстановить данные!
Из этой системы уравнений следуют ряд выводов про восстановление данных для кодов Рида — Соломона (n блоков данных, m блоков кодов избыточности):
Что ещё нужно знать
В описании выше я обхожу стороной ряд важных вопросов, для рассмотрения которых нужно глубже погружаться в математику. В частности, ничего не говорю про следующее:
В конце статьи есть ссылки на литературу по этим важным вопросам.
Выбор n и m
Как на практике выбрать n и m? На практике в системах хранения данных коды избыточности используют для экономии места, поэтому m выбирают всегда меньше n. Их конкретные значения зависят от ряда факторов, в том числе:
Кроме того, хранение данных в нескольких ДЦ накладывает дополнительные ограничения на выбор n и m: при отключении 1 ДЦ данные всё ещё должны быть доступны для чтения. Например, при хранении данных в 3 ДЦ должно выполняться условие: m >= n/2, в противном случае возможна ситуация, когда данные недоступны для чтения при отключении 1 ДЦ.
3. LRC — Local Reconstruction Codes
Для восстановления данных с помощью кодов Рида — Соломона приходится использовать n произвольных блоков данных. Это очень существенный минус для распредёленных систем хранения данных, ведь для восстановления данных на одном сломанном диске придётся читать данные с большинства остальных, создавая большую дополнительную нагрузку на диски и сеть.
Наиболее часто встречающиеся ошибки — недоступность одного блока данных из-за поломки или перегруженности одного диска. Можно ли как-то уменьшить избыточную нагрузку для восстановления данных в таком (наиболее частом) случае? Оказывается, можно: специально для этого существуют коды избыточности LRC.
LRC (Local Reconstruction Codes) — коды избыточности, придуманные в Microsoft для применения в Windows Azure Storage. Идея LRC максимально проста: разбить все блоки данных на две (или более) группы и считать часть блоков кодов избыточности для каждой группы по отдельности. Тогда часть блоков кодов избыточности будет подсчитана с помощью всех блоков данных (в LRC они называются глобальными кодами избыточности), а часть — с помощью одной из двух групп блоков данных (они называются локальными кодами избыточности).
LRC обозначается тремя числам: n-r-l, где n — количество блоков данных, r — количество глобальных блоков кодов избыточности, l — количество локальных блоков кодов избыточности. Для чтения данных при недоступности одного блока данных нужно прочитать только n/l блоков — это в l раз меньше, чем в кодах Рида — Соломона.
Для примера рассмотрим схему LRC 6-2-2. X1–X6 — 6 блоков данных, P1, P2 — 2 глобальных блока избыточности, P3, P4 — 2 локальных блока избыточности.
Блоки кодов избыточности P1, P2 считаются с помощью всех блоков данных. Блок кодов избыточности P3 — с помощью блоков данных X1–X3, блок кодов избыточности P4 — с помощью блоков данных X4–X6.
Остальное делается в LRC по аналогии с кодами Рида — Соломона. Уравнения для подсчёта слов блоков кодов избыточности будут такими:
Для подбора чисел альфа, бета, гамма, дельта нужно выполнить ряд условий, гарантирующих возможность восстановления данных (то есть решения системы уравнения). Подробнее о них можно прочитать в статье.
Также на практике для подсчёта локальных кодов избыточности P3, P4 применяют операцию XOR.
Из системы уравнений для LRC следует ряд выводов:
Таким образом, LRC выигрывает у кодов Рида — Соломона в восстановлении данных после одиночных ошибок. В кодах Рида — Соломона для восстановления даже одного блока данных нужно использовать n блоков, а в LRC для восстановления одного блока данных достаточно использовать n/l блоков (n/2 в нашем примере). С другой стороны, LRC проигрывает кодам Рида — Соломона по максимальному количеству допустимых ошибок. В примерах выше коды Рида — Соломона могут восстановить данные при любых 4 ошибках, а для LRC существует 2 комбинации из 4 ошибок, когда данные восстановить нельзя.
Что более важно — зависит от конкретной ситуации, но зачастую экономия избыточной нагрузки, которую даёт LRC, перевешивает чуть меньшую надёжность хранения.
4. Другие коды избыточности
Помимо кодов Рида — Соломона и LRC, есть много других кодов избыточности. Разные коды избыточности используют разную математику. Вот некоторые другие коды избыточности:
5. Использование в Яндексе
Ряд инфраструктурных проектов Яндекса применяет коды избыточности для надёжного хранения данных. Вот несколько примеров:
В MDS используются коды избыточности LRC, схема 8-2-2. Данные с кодами избыточности пишутся на 12 разных дисков в разных серверах в 3 разных ДЦ: по 4 сервера в каждом ДЦ. Подробнее об этом читайте в статье.
В YT используются как коды Рида — Соломона (схема 6-3), которые были реализованы первыми, так и коды избыточности LRC (схема 12-2-2), причём LRC — предпочтительный способ хранения.
В YDB используются коды избыточности, основанные на even-odd (схема 4-2). Про коды избыточности в YDB уже рассказывали на Highload.
Применение разных схем кодов избыточности обусловлено разными требованиями, предъявляемыми к системам. Например, в MDS данные, хранимые с помощью LRC, размещаются сразу в 3 ДЦ. Нам важно, чтобы данные оставались доступными для чтения при выходе из строя 1 любого ДЦ, поэтому блоки должны быть распределены по ДЦ так, чтобы при недоступности любого ДЦ количество недоступных блоков было не больше допустимого. В схеме 8-2-2 можно разместить по 4 блока в каждом ДЦ, тогда при отключении любого ДЦ будет недоступно 4 блока, и данные можно будет читать. Какую бы схему мы ни выбрали при размещении в 3 ДЦ, в любом случае должно быть (r + l) / n >= 0,5, то есть избыточность хранения будет минимум 50%.
В YT ситуация другая: каждый кластер YT целиком располагается в 1 ДЦ (разные кластеры в разных ДЦ), поэтому там нет такого ограничения. Схема 12-2-2 даёт избыточность 33%, то есть хранить данные выходит дешевле, при этом они также могут переживать до 4 одновременных отключений дисков, как и схема в MDS.
Есть ещё много особенностей применения кодов избыточности в системах хранения и обработки данных: нюансы восстановления данных, влияние восстановления на время выполнения запросов, особенности записи данных и т. д. Я собираюсь отдельно рассказать об этих и других особенностях применения кодов избыточности на практике, если тема будет интересна.
Кодирование информации и избыточность кода
Любое сообщение, может быть представлено в различной форме, то есть закодировано различными способами. Разные способы кодирования неравноценны по занимаемому ими количеству информации. Оптимальным кодом будет тот, при использовании которого среднее значение энтропии, приходящееся на один символ, равно энтропии источника информации.
Чем выше избыточность кода, тем больше вероятность безошибочной передачи информации, но тем больший объём требуется для её хранения и большая пропускная способность канала передачи. Естественные человеческие языки характеризуются очень высокой степенью избыточности, также велика избыточность генома высших организмов, хранящегося в молекулах ДНК.
Величина \(H /Q\) называется экономичностью кода. Для оптимального кода \(H /Q=1\) а избыточность отсутствует, то есть \(E = 0\).
Процесс уменьшения избыточности кодирования называется сжатием информации и применяется для понижения объёма памяти, требуемой для хранения информации. Для сжатия информации, хранящейся в памяти, используются– архиваторы и упаковщики.
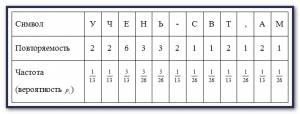
Решение: Подсчитаем количество символов в сообщении, для простоты игнорируя пробелы: N=26. Найдём частоту повторения каждого символа (вероятность в сообщении), составив следующую таблицу, приведенную на скрине слева.
Удельная энтропия (энтропия одного символа в сообщении) в битах на символ, равна \[\tilde H = 5 \cdot \frac<1><<13>><\log _2>13 + \frac<3><<13>><\log _2>\frac<<13>> <3>+ 2 \cdot \frac<3><<26>><\log _2>\frac<<26>> <3>+ 4 \cdot \frac<1><<26>><\log _2>26 \approx \] \[ \approx \frac<5><<13>> \cdot 3.7004 + \frac<3><<13>> \cdot 2.1155 + \frac<6><<26>> \cdot 3.1155 + \frac<4><<26>> \cdot 4.7004 \approx 3.3535\] Полная энтропия сообщения \(H = 3.3535 \cdot 26 = 87.19\) бит. Количество бит, необходимое для кодирования каждого символа одним байтом, составляет \(Q = 208\;\) бит.
Избыточность кода \(E=1-87.19/208=0.58=58%\).