дополнительный код шестнадцатеричного числа
Обратный и дополнительный коды двоичных чисел



Пример перевода
x1=10101-[x1]пр=010101
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Действия с кодами в шестнадцатеричной системе счисления
При сложении дополнении результат может быть получен в прямом или дополнительном коде. Признаком результата в прямом коде является наличие единицы переноса из старших складываемых разрядов. Если перенос ив этих разрядов отсутствует, то результат получен в форме дополнения. И для получения истинного ответа нужно взять дополнение от полученного дополнительного кода и присвоить числу знак «-».
Например, произвести операцию:
Выполним данную операцию вычитания, заменив ее операцией сложения прямого и дополнительного кодов исходных чисел.

+ F57B обратный код числа

F57C дополнительный код числа
Прямой код второго числа 0А3816.
В результате суммирования кода перенос ив старших складываемых разрядов не образуется:
Результат получен в дополнительном коде.

Согласно таблице сложения результат равен +04C16.
Выполним данную операцию, используя коды. Дополнительный код числа (-А3816);

+F5C7 обратный код числа

Прямой код второго числа 0А8416

Перенос из старших складываемых разрядов образуется, поэтому истинный ответ равен + 04С16.
Задание 15.Найдите правильный ответ, определив дополнительный код шестнадцатеричного числа.
Представление целых чисел: прямой код, код со сдвигом, дополнительный код
Выбор способа хранения целых чисел в памяти компьютера — не такая тривиальная задача, как могло бы показаться на первый взгляд. Желательно, чтобы этот способ:
Рассмотрим разные методы представления.
Содержание
Прямой код [ править ]
Достоинства представления чисел с помощью прямого кода [ править ]
Недостатки представления чисел с помощью прямого кода [ править ]
Из-за весьма существенных недостатков прямой код используется очень редко.
Код со сдвигом [ править ]
По сути, при таком кодировании:
Достоинства представления чисел с помощью кода со сдвигом [ править ]
Недостатки представления чисел с помощью кода со сдвигом [ править ]
Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.
Дополнительный код (дополнение до единицы) [ править ]
В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones’ complement).
Алгоритм получения кода числа:
Достоинства представления чисел с помощью кода с дополнением до единицы [ править ]
Недостатки представления чисел с помощью кода с дополнением до единицы [ править ]
Дополнительный код (дополнение до двух) [ править ]
Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two’s complement).
Алгоритм получения дополнительного кода числа:
Длинная арифметика для чисел, представленных с помощью кода с дополнением до двух [ править ]
Достоинства представления чисел с помощью кода с дополнением до двух [ править ]
Недостатки представления чисел с помощью кода с дополнением до двух [ править ]
Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего.
Дополнительный код (представление числа)
Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]
Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2 N для N-битного дополнения до 2). [2]
Содержание
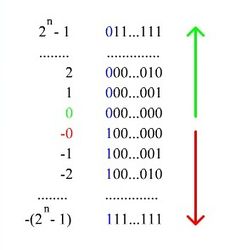
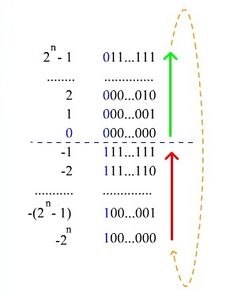
Представление числа в дополнительном коде
При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если же знаковый разряд равен 1, то в остальных разрядах записано отрицательное двоичное число, преобразованное в дополнительный код. Для получения значения, которое противоположно по знаку, все разряды, включая знаковый, инвертируются, а затем к результату добавляется единица.
| Десятичное представление | Код двоичного представления (8 бит) | |
|---|---|---|
| прямой | дополнительный | |
| 127 | 01111111 | 01111111 |
| 1 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 |
| -0 | 10000000 | ——— |
| -1 | 10000001 | 11111111 |
| -2 | 10000010 | 11111110 |
| -3 | 10000011 | 11111101 |
| -4 | 10000100 | 11111100 |
| -5 | 10000101 | 11111011 |
| -6 | 10000110 | 11111010 |
| -7 | 10000111 | 11111001 |
| -8 | 10001000 | 11111000 |
| -9 | 10001001 | 11110111 |
| -10 | 10001010 | 11110110 |
| -11 | 10001011 | 11110101 |
| -127 | 11111111 | 10000001 |
| -128 | ——— | 10000000 |
При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):
| 10-ричная система счисления («обычная» запись) | 10-ричная система счисления, дополнительный код |
|---|---|
| . | . |
| 13 | 0013 |
| 12 | 0012 |
| 11 | 0011 |
| 10 | 0010 |
| 9 | 0009 |
| 8 | 0008 |
| . | . |
| 2 | 0002 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 9999 |
| -2 | 9998 |
| -3 | 9997 |
| -4 | 9996 |
| . | . |
| -9 | 9991 |
| -10 | 9990 |
| -11 | 9989 |
| -12 | 9988 |
| . | . |
Преобразование дополнительного кода
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1
Допишем слева знаковый единичный разряд
Для обратного преобразования используется тот же алгоритм. А именно:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1 и проверим, сложив с дополнительным кодом
Дополнительный код для десятичных чисел
Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).
Дополнительный код (представление числа)
Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]
Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2 N для N-битного дополнения до 2).
Содержание
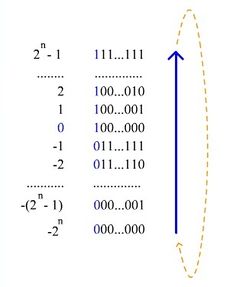
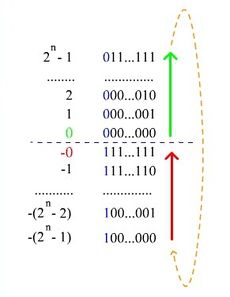
Представление отрицательного числа в дополнительном коде
При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно 
| Десятичное представление | Код двоичного представления (8 бит) | ||
|---|---|---|---|
| прямой | обратный | дополнительный | |
| 127 | 01111111 | 01111111 | 01111111 |
| 1 | 00000001 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 | 00000000 |
| -0 | 10000000 | 11111111 | — |
| -1 | 10000001 | 11111110 | 11111111 |
| -2 | 10000010 | 11111101 | 11111110 |
| -3 | 10000011 | 11111100 | 11111101 |
| -4 | 10000100 | 11111011 | 11111100 |
| -5 | 10000101 | 11111010 | 11111011 |
| -6 | 10000110 | 11111001 | 11111010 |
| -7 | 10000111 | 11111000 | 11111001 |
| -8 | 10001000 | 11110111 | 11111000 |
| -9 | 10001001 | 11110110 | 11110111 |
| -10 | 10001010 | 11110101 | 11110110 |
| -11 | 10001011 | 11110100 | 11110101 |
| -127 | 11111111 | 10000000 | 10000001 |
| -128 | — | — | 10000000 |
Дополнительный код для десятичных чисел
Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).
При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):
| 10-ричная система счисления («обычная» запись) | 10-ричная система счисления, дополнительный код |
|---|---|
| . | . |
| 13 | 0013 |
| 12 | 0012 |
| 11 | 0011 |
| 10 | 0010 |
| 9 | 0009 |
| 8 | 0008 |
| . | . |
| 2 | 0002 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 9999 |
| -2 | 9998 |
| -3 | 9997 |
| -4 | 9996 |
| . | . |
| -9 | 9991 |
| -10 | 9990 |
| -11 | 9989 |
| -12 | 9988 |
| . | . |
Преобразование в дополнительный код
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1
Допишем слева знаковый единичный разряд
Для обратного преобразования используется тот же алгоритм. А именно:
Инвертируем все разряды числа, получая таким образом обратный код:
Добавим к результату 1 и проверим, сложив с дополнительным кодом
p-адические числа
В системе p-адических чисел изменение знака числа осуществляется преобразованием числа в его дополнительный код. Например, если используется 5-ричная система счисления, то число, противоположное 1000. (1) равно 4444. (−1).