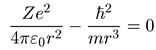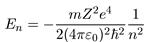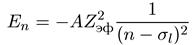движение частицы в кулоновском поле

Заряженная частица в кулоновском поле

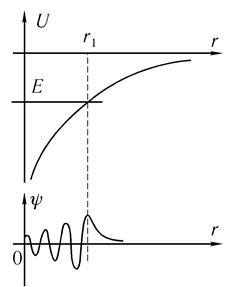
Перейдем к задаче о движении заряженной частицы в кулоновском потенциале (рис. 5.5). Для нас это одна из самых интересных задач, поскольку она описывает состояния электрона в атоме.

Мы уже не раз обсуждали вопрос о том, как найти основное состояние квантовой системы — надо минимизировать, с учетом соотношения неопределенностей, полную энергию. Для электрона, находящегося в кулоновском поле ядра с зарядом Ze, полная энергия определяется выражением

(5.37)

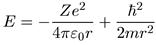
Дифференцирование этого выражения по r приводит к следующему условию для минимального значения энергии:

(5.39)

Мы получили значение боровского радиуса для элек-

трона в поле ядра с зарядом Ze. Такой атом называется водородоподобным. Энергию основного состояния можно найти, подставляя

(5.40)

Аналогичным образом могут быть найдены возбужденные состояния. Волновые функции высших квантовых состояний, согласно осцилляционной теореме, имеют п узлов. Поэтому характерная длина волны А такого состояния будет равна 2тгг/п, что приводит к увеличению кинетической энергии этих состояний. Действительно, электрон локализован в пространстве в области размером порядка А, и поэтому его импульс, согласно соотношению неопределенностей, может быть оценен как

а кинетическая энергия

n 2 ћ 2 /(2mr 2 ). (5.42)

Если провести минимизацию полной энергии, как это делалось выше, то мы

получим для состояния с квантовым числом п

(5.43)

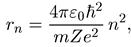
что соответствует радиусу его боровской орбиты, а для энергии этого состояния:

Фактически, дискретные значения энергии электрона в атоме следуют из

Мы предположили, что радиус орбиты r имеет фиксированное значение.

Согласно квантовой механике радиусы орбит «разбросаны» в окрестности

классически устойчивой орбиты. В качестве оценки взято значение r, которое соответствует минимуму энергии Е(r). В действительности электрон может находиться с разной вероятностью на любом расстоянии от ядра.

Наше упрощение состоит в предположении, что это определенное, равное r расстояние находится из условия минимальности полной энергии. Поэтому нельзя доверять числовому множителю впереди полученной формулы, хотя он случайно и оказался правильным. Однако всему остальному, а главное, зависимости от квантового числа n, доверять можно.

Отметим также, что в формулу (5.44) для уровней энергии атома водорода, строго говоря, входит не масса электрона, а приведенная масса системы протон-электрон. Поэтому спектры энергии, например, обычного водорода и его тяжелого изотопа — дейтерия — несколько отличаются друг от друга (так называемый изотопический сдвиг). Существование данного эффекта экспериментально наблюдается не только для водорода, что вполне понятно, поскольку полученное решение справедливо для любой «водородоподобной» системы — системы из двух частиц с противоположными зарядами,

274 m_е). В этих и других такого рода доподобных системах эффект изотопического сдвига сказывается особенно заметно.

где σ_l — поправка на неточечность, зависящая от орбитального движения

электрона (от типа симметрии его движения), a Z_эф — эффективный заряд ядра, учитывающий экранирующее действие электронов замкнутой оболочки.

Одно замечание: при решении мы считали, что ψ-функция — это функция

только расстояния частицы от кулоновского центра, а не угловых переменных, т. е. искали сферически симметричные решения. Позже мы выясним, чему соответствуют решения, не обладающие сферической симметрией. Сейчас лишь отметим, что решение полной задачи не приводит к появлению новых уровней энергии.

Источник

Движение частицы в кулоновском поле

Название работы: Движение в кулоновском поле притяжения (задача Кеплера). Классификация орбит при финитном и инфинитном движении

Предметная область: Физика

Описание: Лекция 10. Движение в кулоновском поле притяжения задача Кеплера. Классификация орбит при финитном и инфинитном движении В предыдущей лекции мы выяснили при каких значениях энергии движение будет инфинитным финитным а так же определили условия при которых траект

Дата добавления: 2013-07-11

Размер файла: 281 KB

Работу скачали: 27 чел.

Лекция 10. Движение в кулоновском поле притяжения (задача Кеплера). Классификация орбит при финитном и инфинитном движении

Для определения вида траектории (а не самого закона движения), совершенно не важен выбор знака перед интегралом в формуле (1). Кроме того, в астрономии принято выбирать так, чтобы в начальный момент времени, тело находилось на наименьшем расстоянии от центра, т.е. в перигелии орбиты. С учетом сказанного, выражение (1) для нашей конкретной задачи, можно записать в виде:

Используя выражения для параметра и эксцентриситета, введенные в предыдущей лекции, получим:

Легко видеть, что второе слагаемое равно нулю. Поэтому:

Это и есть уравнение семейства траекторий в поле притяжения в полярных координатах.

Это и есть уравнение траекторий в декартовых координатах.

Отсюда видно, что уравнение траектории при финитном движении принимает канонический вид:

Это есть уравнение эллипса с полуосями и с началом координат в точке :

В таблице 9.1 приведены значения нескольких характерных точек траектории при финитном движении, рассчитанные по полученным выше формулам.

Рис.1 Орбиты при финитном движении частицы при различных

Чтобы вычислить время обращения по эллиптической орбите, т.е. период обращения воспользуемся законом сохранения момента импульса:

Заметим, что период зависит только от энергии частицы.

Уравнение (13) есть уравнение параболы в области (красная кривая на рисунке 2.

Рис.9.2 Орбиты при инфинитном движении частицы

при различных эксцентриситетах орбиты.

Источник

1.3. Движение заряженной частицы в кулоновском поле

(1.4)

(1.5)

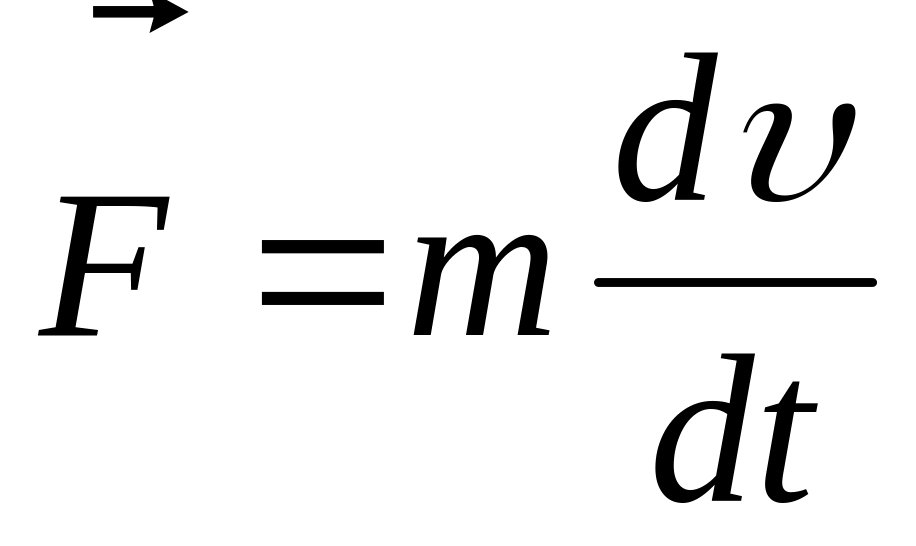
В системе координат, начало которой привязано к телу c большой массой и зарядом Q, уравнения модели имеют вид:

(1.6)

(1.7)

Решение. Задачу решим методом Эйлера. Формулы, по которым проводятся вычисления, имеют вид

Введем обозначения и присвоим им значения и вычислим некоторые вспомогательные величины.

1. В ячейке С1 задано значение первоначального угла =B2*3,14/180

1. В ячейках В2-В6 заданы входные параметры

1. В ячейке А11 задано начальное значение координаты Х

1. В ячейке В11 задано начальное значение координаты У

1. В ячейке С11 вычислено =B3*COS(C2)

6. В ячейке D11 вычислено =B3*SIN(C2)

Вычисления производятся в строке №12 по формулам

7. В ячейке А12 по формуле =A11+C11*B$7

5. В ячейке B12 по формуле =B11+D11*B$7

9. В ячейке C12 по формуле

10. В ячейке D12 по формуле

Остальные значения координат и скоростей получаем, растягивая мышью выделенную строку №12 значений данных по вертикали.

Источник

Учебники

Журнал «Квант»

Общие

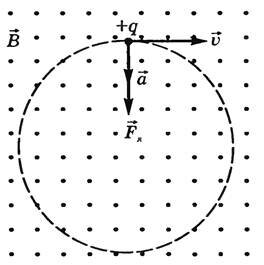
Движение заряженных частиц в электрических и магнитных полях

На заряженную частицу в электростатическом поле действует кулоновская сила, которую можно найти, зная напряженность поля в данной точке\[

\vec F = q \vec E\]. Эта сила сообщает ускорение \(

\vec a= \frac <\vec F> =\frac \), где m — масса заряженной частицы. Как видно, направление ускорения будет совпадать с направлением \(

\vec E\), если заряд частицы положителен (q > 0), и будет противоположно \(

\vec E\), если заряд отрицателен (q \(

F_l = ma_c; qBv = \frac \Rightarrow R =\frac . \)

\frac q m \) — называют удельным зарядом частицы.

Период вращения частицы

то есть период вращения не зависит от скорости частицы и радиуса траектории. На этом основано действие циклотрона.

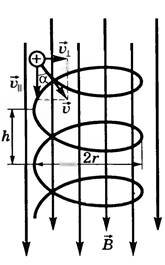
3. Скорость заряженной частицы направлена под углом \(

Движение частицы можно представить в виде суперпозиции равномерного прямолинейного движения вдоль поля со скоростью \(

v_ <\lVert>= v \cos \alpha \) и движения по окружности с постоянной по модулю скоростью \(

v_ <\perp>= v \sin \alpha\) в плоскости, перпендикулярной полю. Радиус окружности определяется аналогично предыдущему случаю, только надо заменить \(

v_ <\perp>= v \sin \alpha\), то есть

В результате сложения этих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю. Шаг винтовой линии

h = v_ <\lVert>\cdot T = v \cos \alpha \cdot T = \frac <2 \pi mv \cos \alpha>\)

Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость заряженной частицы составляет угол α с направлением вектора \(

\vec B\) неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, тο R и h уменьшаются с ростом B. На этом основана фокусировка заряженных частиц в магнитном поле.

Если на движущуюся заряженную частицу помимо магнитного поля с индукцией \(

\vec B\) действует одновременно и электростатическое поле с напряженностью \(

\vec E\), то равнодействующая сила, приложенная к частице, равна векторной сумме электрической силы и силы Лоренца\[

\vec F_e = \vec F_L\]. Характер движения и вид траектории зависят в данном случае от соотношения этих сил и от направления электростатического и магнитного полей.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C.326-327.

Источник

Движение в кулоновском поле

14.1. Принцип причинности в классической и квантовой механике

В классической механике состояние системы задается с помощью координат и скоростей частиц. Зная начальное значение координат и скоростей можно с помощью уравнения второго закона Ньютона рассчитать состояние системы в любой последующий момент времени, т.е. точно определить координаты и скорости всех частиц.

В квантовой механике состояние системы описывается волновой функцией. Если известна волновая функция в начальный момент времени, то из уравнения Шредингера

(14.1)

можно найти волновую функцию системы в любой последующий момент времени.

Одномерное уравнение Шредингера для стационарного состояния в случае свободной частицы

. (14.2)

Запишем уравнение (14.2) в виде

,

где .

,

Положим , тогда

. (14.3)

14.2. Движение частицы в одномерном потенциальном ящике с бесконечно высокими стенками

Уравнение для стационарных состояний частицы, движущейся в силовом поле с потенциальной энергией U(r)

. (14.4)

Потенциальная энергия частицы в «ящике»:

Найдем решение уравнения (14.4) при условии

.

,

.

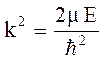
Решение будем искать в виде

На границах ящика, при x = 0 и x = a:

Отсюда находим: y(0) = с₁ = 0,

где .

Собственные волновые функции

. (14.5)

, (14.6)

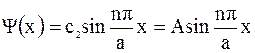
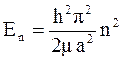
Плотность вероятности обнаружить частицу в ящике

.

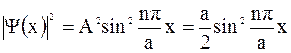
Постоянную А находим из условия нормировки волновых функций

,

,

.

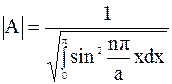
Постоянная А зависит от координаты частицы и квантового числа n, характеризующего уровень энергии.

Собственная волновая функции и собственная энергия частицы в бесконечном прямоугольном ящике дискретны.

Наименьшее значение энергии частицы

.

14.3. Движение в поле с центральной симметрией

В уравнении (14.4) запишем оператор Лапласа в сферических координатах:

.

где — оператор квадрата момента импульса.

Получим уравнение Шредингера

. (14.7)

Решение будем искать в виде

Подставим (14.8) в уравнение (14.7). Учитывая, что

,

получим уравнение для радиальной части волновой функции

.

Введем вместо функции R(r) функцию c(r)

.

Для c(r) находим уравнение

.

При r = 0 волновая функция должна быть конечной, отсюда c(0) = 0. Введем эффективную потенциальную энергию

,

где вторая часть выражения называется центробежной энергией.

Уравнение (14.7) свелось к уравнению одномерного движения с эффективной потенциальной энергией

. (14.9)

Радиальная составляющая волновой функции R(r) зависит от вида потенциальной энергии.

Угловая часть Y_lm(q,j) определяется величиной момента импульса (азимутальное квантовое число l) и его проекцией на ось z (магнитное квантовое число m).

Состояния с заданным моментом импульса обозначаются малыми буквами латинского алфавита:

l = 0 1 2 3 4 5 6 7

Квантовое число l определяет четность состояния. При преобразовании инверсии (отражении) волновая функция изменяется по закону

.

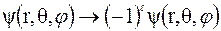
Четное квантовое число соответствует четным состояниям (s,d,g. ), а при нечетном состояния (p,d,f,h. ) состояния являются нечетными.

Вероятность dW(q,j) обнаружить частицу в телесном угле dW в направлении, определяемом углами q,j:

.

.

,

.

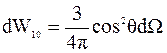
Таким образом, можно сделать общие заключения о поведении волновой функции, не указывая конкретный вид потенциальной энергии U(r).

14.4. Движение в кулоновском поле

Потенциальная энергия электрона, движущегося в поле ядра с зарядом Ze

.

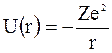
Уравнение Шредингера для радиальной функции

.

Найдем энергии состояний, принадлежащих дискретному энергетическому спектру. Эти состояния соответствуют движению электрона в атоме, E
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.019 сек.)

Источник