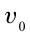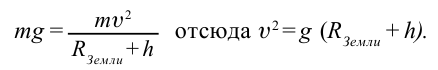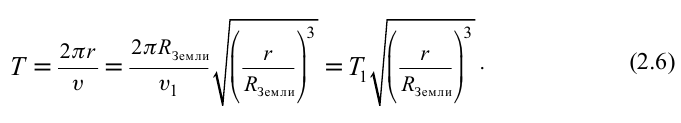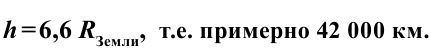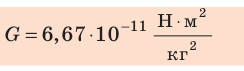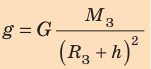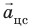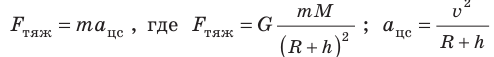движение тел в гравитационном поле

Содержание:

Движение в гравитационном поле:

Вы в 7-ом классе узнали о том, что Земля создает вокруг себя постоянное поле притяжения и с помощью этого поля притягивает к себе все тела. Значит, на любое движение на Земле оказывает свое влияние поле притяжения. Представим, что с вершины горы брошено какое-либо тело в горизонтальном направлении со скоростью

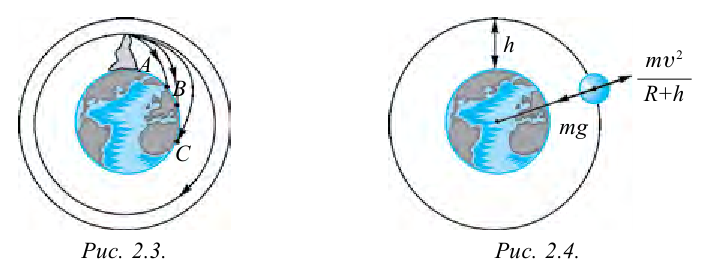
Если скорость тела увеличить, то оно упадет в точке или . Начиная с некоторой определенной скорости тела не падают на Землю, а начинают вращаться вокруг Земли. Такое тело становится искусственным спутником Земли. Движение искусственного спутника является движением в поле притяжения. Почему спутник не падает на Землю? При каких скоростях
это происходит? Сначала рассмотрим силы, действующие на спутник. На спутник постоянно действует сила притяжения Земли. Чтобы снизить сопротивление воздуха, спутник нужно поднять в самые верхние слои атмосферы.

На высоте 300 – 400 км от поверхности Земли сопротивление воздуха почти отсутствует. Значит, на таких высотах силу притяжения Земли компенсирует центробежная сила, которая появляется благодаря скорости спутника (рис. 2.4).
В этом случае:

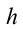
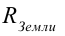
В случае, когда высоту по сравнению с радиусом Земли можно не учитывать,

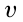
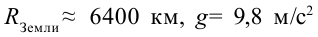
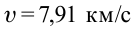
Чтобы вычислить значение , принимаем , соответственно .
Эта скорость называется первой космической скоростью.
Искусственный спутник Земли, который двигается с такой скоростью, делает один оборот вокруг Земли за время: .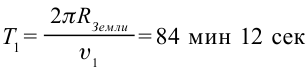

На практике время, за которое спутник совершает один оборот, больше чем расчетное время. Причина этого явления в том, что радиус орбиты спутника и радиус Земли отличаются друг от друга.

Таким образом, скорости спутников, вращающихся на орбитах с большими радиусами, будут меньше, чем скорости спутников, вращающихся на орбитах, близких к поверхности Земли.

Период вращения таких спутников вычисляется по формуле:

Здесь: 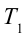– период вращения спутников, вращающихся на орбитах, близких к поверхности Земли.

Используя формулу периода вращения спутника, вращающегося на произвольных высотах, можно вычислить необходимое расстояние от Земли, на котором спутник должен зафиксироваться. На какой высоте должен двигаться спутник, чтобы период его вращения был равен 24 часам? Расчеты показали, что высота составляет:

Такая орбита называется геостационарной орбитой.

Впервые на нашей планете 4 октября 1957 года на территории бывшего СССР был запущен первый искусственный спутник Земли. Спутник имел форму шара диаметром 58 см и массой 83,6 кг. Этот спутник совершил вокруг Земли 1400 оборотов, т.е. преодолел расстояние в 60 миллионов километров. А 12 апреля 1961 года первый человек полетел в космос. Первый космонавт Юрий Алексеевич Гагарин был гражданином бывшего СССР. 20 июля 1969 года американские астронавты Нейл Армстронг и Эдвин Олдрин впервые совершили посадку на Луну.

Для того чтобы долететь до планет Солнечной системы, космический корабль должен преодолеть вторую космическую скорость, равную 11,2 км/с.
Для достижения далеких звезд потребуется преодолеть силу притяжения Солнечной системы, т.е. космический корабль должен двигаться с третьей космической скоростью. Величина третьей космической скорости равна 16,7 км/с.

Среди космонавтов, которые многократно летали в космос, наш соотечественник В. Джанибеков и представитель узбекской нации С. Шарипов.

Гравитационное поле и сила притяжения

Шесть из восьми планет Солнечной системы были открыты благодаря наблюдениям за звездным небом. Именно так в 1781 г. английский астроном Джон Гершель открыл Уран. Впрочем, планета вела себя «странно»: ее орбита не соответствовала расчетам, основанным на законе всемирного тяготения. Ученые предположили, что рядом с Ураном есть еще одна планета, и начали искать ее с помощью. математики.

Рассчитать орбиту новой планеты удалось англичанину Джону Адамсу и французу Урбену Леверье. 23 августа 1846 г. немецкий астроном Иоганн Галле навел телескоп на указанное Леверье место и. увидел планету! Нептун — восьмая планета Солнечной системы — стал первым космическим объектом, открытым «на кончике пера».

Как определить силу гравитационного притяжения

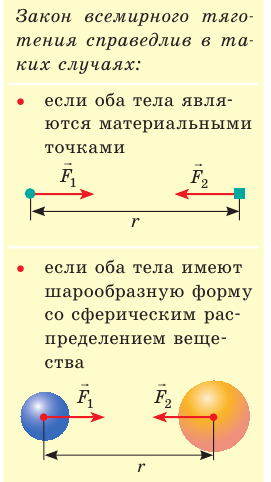
Гравитационное взаимодействие — взаимодействие, свойственное всем телам во Вселенной и проявляющееся в их взаимном притяжении друг к другу. Гравитационное взаимодействие происходит посредством гравитационного поля, которое существует вокруг любого тела: звезды, планеты, человека, молекулы и т. д. Выведем закон всемирного тяготения, следуя логике рассуждений Ньютона, который и установил данный закон.

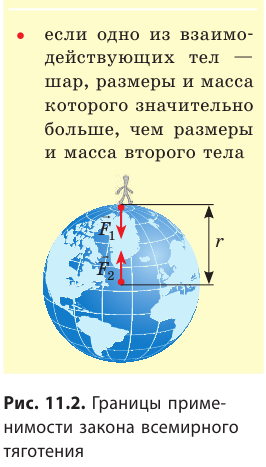
Закон всемирного тяготения имеет определенные границы применимости (рис. 11.2). Только в XX в. было установлено: когда гравитационные поля настолько сильны, что разгоняют тела до скоростей порядка скорости света, или когда частицы, пролетающие вблизи массивных тел, еще на отдалении имеют скорость, сравнимую со скоростью света, силу гравитационного притяжения нельзя рассчитать по закону всемирного тяготения. В общем случае тяготение описывается общей теорией относительности.

Как измерить гравитационную постоянную

Гравитационная постоянная G — одна из фундаментальных констант в физике. По современным данным, значение гравитационной постоянной составляет:

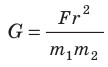
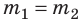
Из формулы (3) следует: . То есть, если r= 1 м, а =1 кг, то G численно равна F. Гравитационная постоянная численно равна силе гравитационного притяжения двух материальных точек массой 1 кг каждая, находящихся на расстоянии 1 м друг от друга.

Измерить гравитационную постоянную достаточно сложно: гравитационное притяжение между телами становится заметным только при очень большой массе хотя бы одного из тел.

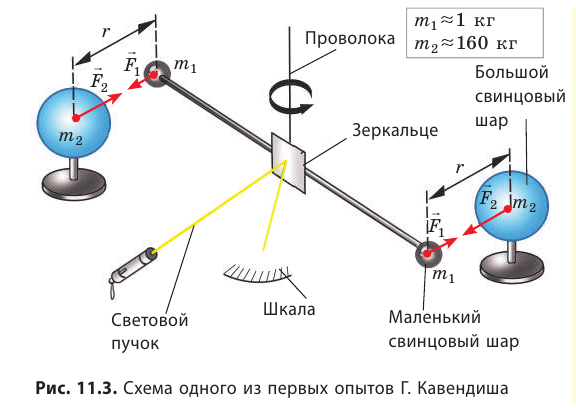
Гравитационную постоянную впервые измерил английский ученый Генри Кавендиш (1731–1810) в 1798 г. с помощью крутильных весов (рис. 11.3).

Как «взвесить» Землю

Опыт Г. Кавендиша еще называют «взвешиванием Земли». Как можно измерить массу Земли и любой другой планеты? Вспомним о силе тяжести.

Сила тяжести 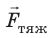— это сила, с которой Земля (или другое астрономическое тело) притягивает к себе тела, находящиеся на ее поверхности или вблизи нее.

Сила тяжести направлена вертикально вниз и приложена к точке, которую называют центром тяжести тела.

Приравняв правые части формул (1) и (2), получим формулу для вычисления ускорения свободного падения:

Проанализировав последнюю формулу, приходим к следующим выводам.

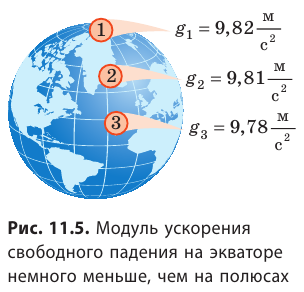
Отметим, что из-за вращения Земли, а также из-за того, что форма Земли — геоид, ускорение свободного падения зависит от географической широты местности (рис. 11.5).

Ускорение свободного падения в определенной местности может отличаться от его средних значений на данной широте. Причины — в неоднородности земной коры, наличии гор и впадин; в различной плотности пород, залегающих в недрах Земли. Так, уменьшение ускорения свободного падения часто свидетельствует о залежах торфа, нефти, газа; увеличение — о залежах металлических руд. Метод поиска залежей полезных ископаемых по точному определению ускорения свободного падения называют гравиметрической разведкой.

Первая космическая скорость

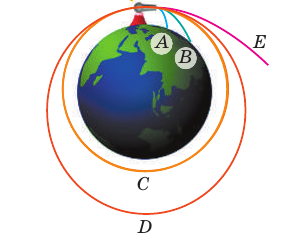
Представим, что мы стреляем из пушки в горизонтальном направлении, с каждым выстрелом увеличивая скорость движения ядра. Траектория движения ядер будет параболической, и каждый раз ядра будут падать все дальше. Если представить, что Земля плоская, на этом наш эксперимент можно было бы и завершить, но Земля имеет форму шара, поэтому с каждым выстрелом она все больше и больше будет «уходить» из-под ядра (рис. 11.6). Теперь представим, что сопротивление воздуха отсутствует, а мы придали ядру такую большую скорость, что оно облетело вокруг Земли и вернулось к месту выстрела.

При этом ядро не остановится, а будет и дальше двигаться с неизменной скоростью, «наматывая круги» вокруг планеты. Другими словами, мы получим искусственный спутник Земли.

Рис. 11.6. Движение тела под действием силы тяжести (по рисунку И. Ньютона): ядра A и B падают на Землю, ядро C выходит на круговую орбиту, D — на эллиптическую, ядро E летит в открытый космос

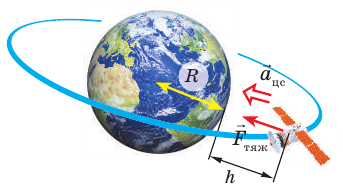
Рис. 11.7. На спутник, движущийся по круговой орбите на высоте h над поверхностью планеты, действует одна сила — сила тяжести 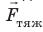, которая и придает спутнику центростремительное ускорение

Скорость, которую надо сообщить объекту, чтобы он двигался вокруг планеты по круговой орбите, называют первой космической скоростью.

Первую космическую скорость v можно вычислить, учитывая, что именно сила тяжести придает телу центростремительное ускорение (рис. 11.7). По второму закону Ньютона:

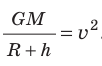
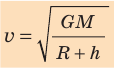
Следовательно, . Отсюда получаем формулу для вычисления первой космической скорости движения спутника на высоте h над поверхностью планеты: .

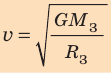
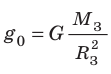
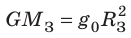
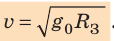
Для случаев вблизи поверхности Земли (h≈ 0) данная формула принимает вид: . Вспомним, что у поверхности Земли, то есть . После упрощения получим: .

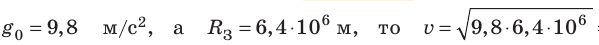
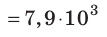
Поскольку =(м/с) — первая космическая скорость у поверхности Земли.

4 октября 1957 г. Советский Союз вывел на орбиту первый искусственный спутник Земли — ПС-1. Его разработали С. П. Королев, М. В. Келдыш, М. К. Тихонравов и другие выдающиеся ученые. ПС-1 представлял собой небольшую сферу диамет ром 58 см и массой 83,6 кг, оснащенную четырьмя антеннами длиной 2,4 и 2,9 м для передачи сигнала.

Спутник отделился от второй ступени ракеты-носителя на 315-й секунде после старта и почти сразу начал передавать сигнал, который слышали не только специалисты, но и радиолюбители практически всех стран. С этого момента начался отсчет космической эры человечества.

«Тот маленький огонек, стремительно двигающийся от края и до края неба. сделал человечество бессмертным», — писал американский писатель-фантаст Рэй Брэдбери. В течение 92 суток полета спутник совершил 1440 оборотов вокруг Земли, после чего сгорел в атмосфере. Траекторию движения спутника на карту звездного неба первыми нанесли наблюдатели Лаборатории космических исследований Ужгородского государственного университета.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Движение тел в гравитационном поле

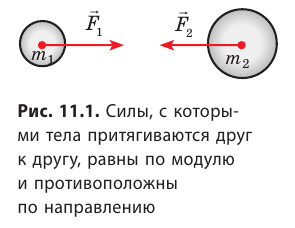
Все тела обладающие массой притягиваются друг к другу. Исаак Ньютон на основе многолетних данных астрономических наблюдений и законов динамики сформулировал закон всемирного тяготения : две любые материальные точки массами m 1 и m 2 притягиваются друг к другу вдоль линии соединяющей точки с силой прямо пропорциональной произведению масс точек и обратно пропорциональной квадрату расстояния (r) между ними:

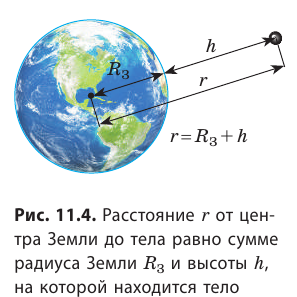
Земля не является «материальной точкой» для тел, расположенных на ее поверхности. Теоретически доказано, что сила, с которой Земля притягивает тела, расположенные вне ее, равна силе, которую создавала бы материальная точка массой (М), равной массе Земли, и расположенная в центре Земли. Назовем силой тяжести силу, с которой тело взаимодействует с планетой, вблизи которой оно находится.

В соответствии с законом всемирного тяготения на материальную точку массой (m) со стороны Земли будет действовать сила тяжести, равная

Если тело движется с ускорением равным ускорению силы тяжести, то вес тела будет равен нулю:

1) вес тела равен нулю когда тело движется с ускорением равным ускорению силы тяжести ( ) в лифте вертикально вниз;

Закон всемирного тяготения определяет величину и направление силы всемирного тяготения, но не отвечает на вопрос как осуществляется это взаимодействие. Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения, или гравитационного поля.

1. Напряженность гравитационного поля ( ), силовая характеристика поля, равна силе, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой (это ничто иное как ускорение, с которым тело движется в поле тяготения):

Независимо от своей массы все тела под действием силы тяжести движутся с одинаковым ускорением ( )

Единица измерения [φ]=Дж/кг.

Потенциальная энергия тела в гравитационном поле равна:

Тогда работа гравитационного поля по перемещению тела из точки с потенциалом φ 1 в точку с потенциалом φ 2 равна:

Работа гравитационного поля по перемещению тела между двумя точками не зависит от траектории движения тела, а определяется только разностью потенциалов начальной и конечной точек, на замкнутом пути работа гравитационного поля равна нулю. То есть, сила всемирного тяготения и сила тяжести являются консервативными.

В качестве примера рассмотрим гравитационное поле материальной точки.

Наглядную картину поля представляет набор линий напряженности и эквипотенциальных поверхностей, например, гравитационное поле материальной точки представлено на рисунке (1.8.2).

Мы уже упоминали, что гравитационное поле Земли можно рассматривать, как поле материальной точки расположенной в центре Земли. Тогда потенциальная энергия тела, находящегося на высоте h относительно Земли:

Потенциальная энергия тела на высоте h над поверхностью Земли, равна:

Рассмотрим взаимосвязь между потенциалом и напряженностью поля тяготения.

Элементарная работа, совершаемая полем при малом перемещении тела массой (m), равна

Величина dφ/dl характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения, это ничто иное, как градиент потенциала.

Таким образом, напряженность гравитационного поля численно равна градиенту потенциала гравитационного поля и направлена в сторону его уменьшения:

На Земле приблизительно инерциальными являются системы отсчета, которые покоятся или движутся равномерно и прямолинейно относительно точек на поверхности Земли.

Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, рассматривают три варианта проявления этих сил.

1. Сила инерции возникает при ускоренном поступательном движении системы отсчета и направлена против вектора ускорения неинерциальной системы отсчета :

Действию центробежной силы инерции подвергаются пассажиры в движущемся транспорте на поворотах; летчики при выполнении фигур высшего пилотажа; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах, где они достигают огромных значений. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов) принимаются специальные меры для уравновешивания центробежных сил инерции.

равна произведению удвоенной массы тела на векторное произведение скорости поступательного движения тела относительно системы отсчета и угловой скорости вращения системы отсчета. Эта сила направлена перпендикулярно векторам скорости тела и угловой скорости вращения системы в соответствии с правилом правого винта.

Земля представляет собой вращающуюся систему отсчета и действие силы Кориолиса объясняет ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север (рис.1.8.4), то сила Кориолиса будет направлена вправо по отношению к направлению движения, и тело отклонится на восток. Если тело движется в юг, то сила Кориолиса также направлена вправо по отношению к направлению движения, и тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые. Аналогично можно показать, что в южном полушарии сила Кориолиса, действующая на движущиеся тела, будет направлена влево по отношению к направлению движения.

Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета : произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции):

Обратим еще раз внимание на то, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета, поэтому они не подчиняются третьему закону Ньютона. Два основных положения механики: 1) ускорение всегда вызывается силой; 2) сила всегда обусловлена взаимодействием между телами, в неинерциальных системах отсчета одновременно не выполняются.

Таким образом, силы инерции действуют только в неинерциальных системах отсчета, в инерциальных системах отсчета таких сил не существует.

Все тела независимо от их масс и химического состава, получают в данном гравитационном поле одинаковые ускорения. Поэтому в таком поле они движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают свободно движущиеся тела, если их движение рассматривать относительно какой-либо неинерциальной системы отсчета.

Силы инерции, действующие на тела неинерциальной системе отсчета, пропорциональны их массам и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в «поле сил инерции» эти тела движутся совершенно одинаково, если только одинаковы начальные условия.

Все механические явления и движения в лифте будут в точности такими же, что и в неподвижном лифте, висящем в поле тяжести.

Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции.

Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции.

Принципа эквивалентности Эйнштейна: все физические явления в поле сил тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы.

Принцип эквивалентности гравитационных сил и сил инерции можно рассматривать как принцип эквивалентности гравитационной и инерционной масс тела.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2013

Источник

Лекция 11. Движение в поле гравитации

Движение в поле гравитации

Закон всемирного тяготения. Экспериментальное определение постоянной гравитации. Гравитационное поле, его характеристики. Задача Кеплера. Гравитационная энергия однородного шара. Гравитационный радиус. Гравитационное красное смещение.

Закон всемирного тяготения.

На основе наблюдательных данных Кеплер (1571-1630) установил законы движения планет Солнечной системы:

— каждая планета движется по эллиптической орбите, в одном из фокусов которого находится Солнце;

— радиус-вектор планеты в равные времена описывает равные площади;

— квадраты периодов обращений планет относятся как кубы больших осей соответствующих эллиптических орбит.

Используя эти законы, Ньютон установил закон всемирного тяготения, согласно которому любые два тела (частицы) массами m1 и m2 в вакууме притягиваются друг к другу с центральными силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними:

(11.1)

где – одна из фундаментальных постоянных, называемая постоянной гравитации, — расстояние между частицами (рис.11.1).

Эти силы называются гравитационными силами, или силами всемирного тяготения.

Экспериментальное определение постоянной гравитации.

Опыт Кавендиша (1731-1810). Первое непосредственное доказательство закона (11.1) в лабораторных условиях и численное определение постоянной гравитации были проведены Кавендишем в 1798г. на крутильных весах (рис.11.2). Вблизи концов коромысла, укрепленными одинаковыми шариками массы m, помещались два других больших свинцовых шара массы M каждый, причем , сначала в положении, затем –. Из-за гравитационного притяжения шариков с шарами, коромысло поворачивался соответственно на углы и .

Углы измерялись смещением луча света, отраженного от зеркала З (рис.11.2). В положениях и на коромысло действует крутящий момент пары гравитационных сил , который уравновешивается упругим моментом закрученной нити :

где — длина коромысла, – расстояние между центрами шарика и ближайшего шара, — модуль кручения, который находят из периода крутильных колебаний коромысла

В результате для определения G получаем формулу

где фигурируют только измеряемые величины.

Опыт Жолли (1809-1880). В этом методе используются рычажные весы, на левом плече которых подвешены две чашки, как это показано на рис.11.3. Между чашками неподвижно установлен тяжелый свинцовый шар с узким вертикальным каналом, сквозь который проходит нить, соединяющая чашки. Если на верхнюю чашку положить шарик массы m, то на него будет действовать вниз сила , где — расстояние между центрами шарика и тяжелого шара. Если шарик перевести на нижнюю чашку, то на него будет действовать сила . Следовательно, для восстановления равновесия рычажных весов после перемещения шарика в нижнее положение, надо уменьшить груз на правом плече чашки весов на , откуда и можно найти значение .

Согласно современным представлениям тяготение между телами осуществляется, так называемыми гравитационным полем. Каждое тело создает в окружающем пространстве силовое поле, которое и действует на тела в этой области. Силовой характеристикой этого поля служит его напряженность – сила, действующая на единицу массы пробной частицы массой , помещенной в точке поля:

. (11.2)

Это – не что иное, как ускорение свободного падения частицы в данной точке. Для поля точечной массы m оно, с помощью (11.1), (11.2) выразится формулой

. (11.3)

Энергетической характеристикой гравитационного поля служит его потенциал. Это гравитационный потенциал единицы массы пробной частицы:

. (11.4)

Для поля точечной частицы массы m имеем

. (13.5)

Принцип независимости действия сил для полей приводит к принципу их суперпозиции: гравитационное поле, создаваемое несколькими телами, равно геометрической сумме гравитационных полей, возбуждаемых этими телами в отдельности. Математически этот принцип выражается формулами

. (11.6)

На основе этих формул можно вычислить гравитационное поле любого тела. Для этого надо мысленно разбить тело на малые части, и подсчитать характеристики поля по формулам (11.3), (11.5) и (11.6).

Пользуясь принципом суперпозиции, можно показать (см. задачи), что внешние гравитационные поля однородного шара и шаровой оболочки, выражаются формулами (11.3) и (11.5), и поэтому два однородных шара (сферические оболочки) притягиваются между собой так, как если бы их массы были сконцентрированы в их центрах.

Рассмотрим теперь движение легкой частицы массы m в поле гравитации тяжелой точечной массы , (задача Кеплера). Эта задача, фактически, достаточно хорошо моделирует движения планет в поле гравитации Солнца. Понятно, что в зависимости от меры сообщаемой частице энергии Е, ее движение в поле гравитации точечной массы будет либо финитным (эллипс), либо инфинитным (парабола, или гипербола). Поэтому, задача сводится к нахождению условий финитности, или инфинитности движения частицы.

Так как диссипативные силы отсутствуют, то энергия частицы сохраняется

(11.7)

где – радиальная и азимутальная компоненты скорости, – расстояние частицы до точечной массы.

Используя закон сохранения момента импульса частицы:

, (11.8)

и исключая его помощью азимутальную скорость из (11.7), получим

. (11.9)

Формально это выражение можно рассматривать как энергию одномерно-радиального движения частицы во внешнем поле с эффективным потенциалом

, (11.10)

зависимость которого от силового центра r схематически представлена на рис.11.4.

Так как первый член правой части (11.9) неотрицательная величина, то область пространства, в которой может находиться частица, определится условием . Проведем горизонтальную прямую. Области пространства, соответствующие участкам кривой , которые лежат выше этой прямой, не достигаемы частицей с энергией (рис.11.5).

Если , то прямая пересекает кривую в двух точках поворота, которым соответствуют расстояния от центра и . Движение частицы локализовано в области , т. е. финитно, и соответствует движению по эллипсу. Расстояния и , которые называются перицентром и апоцентром эллиптической орбиты, являются решениями уравнения :

. (11.11)

Введя эксцентриситет траектории как

,

и пользуясь теоремой Виета:

, (11.12)

получим следующую формулу

, (11.13)

которая дает связь формы траектории частицы с параметрами задачи.

Минимуму эффективного потенциала соответствует расстояние от центра и энергия (их легко получить из (11.10)). Подставляя в (11.13), находим соответствующее значение эксцентриситета . Это круговое движение с радиусом орбиты . Из (11.8) для скорости кругового движения получаем

. (11.14)

Если в первое соотношение (13.12) положить (круговое движение), то получится , или . И так как , то для кругового движения получаем . Т. е. при круговом движении сумма полной и кинетической энергий частицы равна нулю.

Уравнение (11.11) дает два вещественных корней лишь в области энергий . Им соответствует эллиптическая орбита со значениями эксцентриситета (рис.11.6).

Большая полуось эллипса имеет длину , а малая полуось – .

Если , то прямая пересечет кривую только в одной точке, соответствующей расстоянию от центра . Двигаясь к центру, частица остановится на расстоянии и меняет направление радиальной скорости в обратную сторону, удаляясь в бесконечность. Это – инфинитное движение, а траектория – гипербола. Наконец, при , движение частицы также инфинитно – но с параболической траекторией (рис.11.7). Так как в бесконечном расстоянии от центра , то здесь . Отсюда следует, что при гиперболическом движении частица приходит в бесконечность с конечной скоростью , а при параболическом движении – с нулевой скоростью. Начальная скорость , которую надо сообщить частице на расстоянии , чтобы она стала двигаться по параболе, называется параболической скоростью. Ее можно определить из (11.7), подставив в него :

,

(11.15)

Сравнивая (11.14) и (131.15), получим .

Полученные здесь формулы применимы к движениям тел в околоземном пространстве, где можно пренебречь сопротивлением атмосферы. В частности, применительно к Земле формулы (11.14) и (11.15) выражают первую (круговую) и вторую (параболическую) космические скорости. Именно такие скорости нужно сообщить телу на поверхности Земли (при этом – радиус Земли), чтобы оно двигался вокруг нее по кругу, или по параболической орбите. Убедитесь сами, что приблизительные значения этих скоростей соответственно равны 8 км/с и 11,2 км/с.

Собственная гравитационная энергия однородного шара.

Тела, которые формировались и удерживаются внутренними силами всемирного тяготения, называются гравитирующими. Таковыми являются планеты, звезды и разнообразные совокупности звезд. Работу внутренних консервативных сил мы характеризовали собственной потенциальной энергией, которая в рассматриваемом случае называется гравитационной. Это – работа гравитационных сил при полном разрушении системы, т. е. при превращении системы в конфигурацию с нулевой гравитационной энергией. Это соответствует ситуации, когда расстояния между всеми частицами бесконечны.

, (11.16)

где мы исключили из первого подынтегрального выражения , пользуясь следующим очевидным соотношением для однородного шара: . Знак минус вызван с выбором конфигурации с нулевой энергией (чтобы достичь ее следует сообщить шару положительную энергию).

, (11.17)

Гравитационное поле вокруг таких сверхплотных образований уже не описываются простыми формулами (11.3),(11.5). Эйнштейн в 1915г. построил релятивистскую теорию гравитации, или общую теорию относительности, в рамках которой и описываются эти объекты и связанные с ними явления. Однако некоторые экзотические явления можно предварительно получить и в рамках Ньютонов теории гравитации с учетом выводов специальной теории относительности. Например, легко убедиться, что круговая скорость у поверхности (в действительности такая поверхность не может находиться в равновесии, а под действием мощных сил гравитации должна безудержно сжиматься к центру) объекта с радиусом (11.17) равна скорости света. Это означает, что световой квант не в состоянии преодолеть притяжение такого объекта и выйти наружу, т. е. их нельзя наблюдать непосредственно. Однако их можно обнаружить по определенным явлениям, если они входят в состав двойной звезды. Такие объекты носят название черных дыр.

Гравитационное красное смещение.

Световой квант, излучаемый гравитирующим телом (звездой), должен тратить определенную энергию для преодоления его гравитационное притяжение. Это – гравитационная энергия кванта света на поверхности тела. Поэтому, энергия преодолевшего притяжение тела светового кванта будет меньше, чем его энергия на поверхности тела. Следовательно, спектры принимаемых на Земле излучений звезд должны быть смещенными в сторону меньших частот (больших длин волн), т. е. в сторону красной границы спектра. Это и называется гравитационным красным смещением спектральных линий излучения звезд.

Для оценки красного смещения спектров излучения звезд рассмотрим световой квант частоты на поверхности звезды массы M и радиуса R (рис.11.9). Полная энергия кванта на поверхности звезды складывается из энергии и его потенциальной энергии , где – масса фотона, а – гравитационный потенциал звезды на ее поверхности. Энергия преодолевшего притяжение звезды и регистрируемого приемником фотона будет (рис.11.9). Применяя закон сохранения энергии к двум описанным состояниям фотона:

,

где пользовались формулой (11.17) для гравитационного радиуса, находим, что относительное смещение частоты отрицательно и равно

. (11.18)

Для обычных звезд отношение мало – порядка , а для нейтронных звезд – порядка 0,1-0,3.

Вообще, гравитационное красное смещение происходит, когда фотон перемещается в поле тяготения из точки с меньшим потенциалом в точку с большим потенциалом. Очевидно, при обратном перемещении получится фиолетовое смещение, т. е. частота фотона будет расти. Паунд и Ребекка в 1960г. регистрировали изменение частоты -излучения в лабораторных условиях при перемещении -кванта в вертикальном направлении всего в 22 м. Относительное изменение длины волны γ-кванта при этом составляло . В этих опытах было получено , что является блестящим подтверждением явления гравитационного смещения спектральных линий.

● Сформулируйте законы Кеплера.

● Для каких тел сформулирован закон всемирного тяготения?

● Какие физические параметры характеризуют гравитационное поле?

● Опишите опыты измерения постоянной гравитации.

● Каковы условия финитного (инфинитного) движения частицы в поле

● Выводите формулы космических скоростей.

● Выводите формулу собственной гравитационной энергии однородного

● Что такое гравитационный радиус?

● Как можно с помощью спектра обнаружить гравитационное красное

● Каково физическое следствие от равенства инертной и гравитационной

1. Абрамян основы механики. Изд. ЕГУ, 1997 – 370 стр. (на армянском яз.).

2. Сивухин курс физики. Механика. М., Наука, 1979 – 520 стр.

5. Иродов по общей физике. M., Наука, 1979; «Лань», 2001 – 416 стр.

Источник