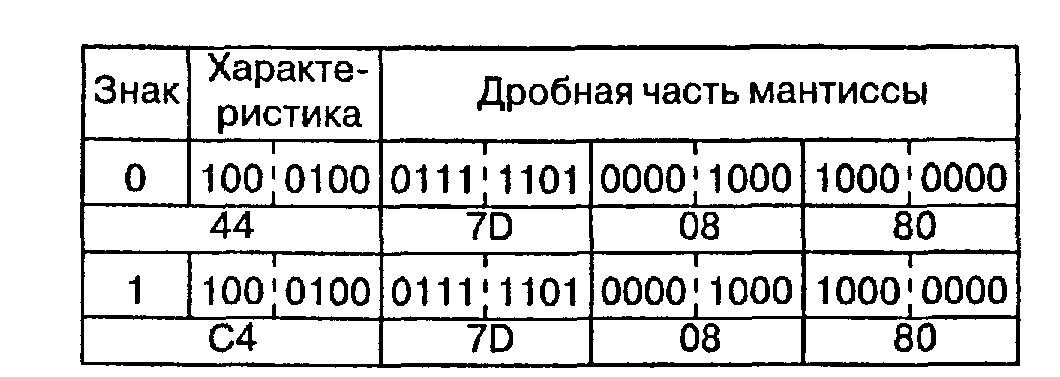
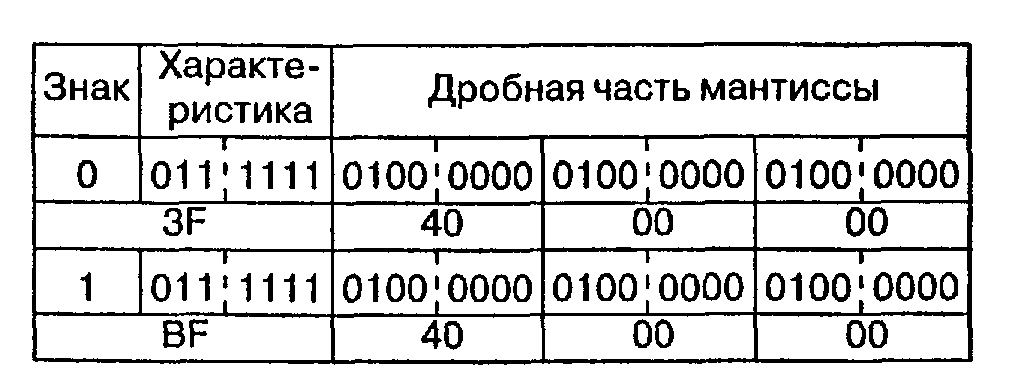
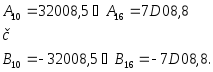двоичный код с фиксированной точкой
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Когда десятичные числа с фиксированной запятой отображаются для чтения человеком, цифры дроби обычно отделяются от цифр целой части символом системы счисления (обычно ‘.’ На английском языке, но ‘,’ или каким-либо другим символом на многих других языках). Однако внутри нет разделения, и различие между двумя группами цифр определяется только программами, которые обрабатывают такие числа.
СОДЕРЖАНИЕ
Представление
| Представленная ценность | Внутреннее представительство |
|---|---|
| 0,00 | 0 |
| 0,5 | 50 |
| 0,99 | 99 |
| 2 | 200 |
| −14,1 | −1410 |
| 314,160 | 31416 |
Выбор масштабных коэффициентов
Однако иногда могут использоваться другие коэффициенты масштабирования, например дробное количество часов может быть представлено как целое число секунд; то есть как число с фиксированной точкой с масштабным коэффициентом 1/3600.
Даже при самом тщательном округлении значения с фиксированной точкой, представленные с коэффициентом масштабирования S, могут иметь ошибку до ± 0,5 в сохраненном целом числе, то есть ± 0,5 S в значении. Следовательно, меньшие коэффициенты масштабирования обычно дают более точные результаты.
| ж | S | δ | V мин | V макс. |
|---|---|---|---|---|
| −3 | 1/2 −3 = 8 | 4 | — 262 144 | + 262 143 |
| 0 | 1/2 0 = 1 | 0,5 | — 32 768 | + 32 767 |
| 5 | 1/2 5 = 1/32 | 000 00 | +1023. 968 75 | |
| 14 | 1/2 14 = 1/16 384 | 000 031 | −2. 000 000 000 000 00 | +1. 999 938 964 843 75 |
| 15 | 1/2 15 = 1/32 768 | 000 016 | −1. 000 000 000 000 000 | +0. 999 969 482 421 875 |
| 16 | 1/2 16 = 1/65 536 | 000 008 | −0. 500 000 000 000 000 0 | +0. 499 984 741 210 937 5 |
| 20 | 1/2 20 = 1/1 048 576 | 000 000 5 | −0. 031 250 000 000 000 000 00 | +0. 031 249 046 325 683 593 75 |
Точные значения
Сравнение с плавающей точкой
Программы, использующие вычисления с фиксированной точкой, обычно более переносимы, чем программы, использующие вычисления с плавающей точкой, поскольку они не зависят от доступности FPU. Это преимущество было особенно сильным до того, как стандарт IEEE с плавающей запятой получил широкое распространение, когда вычисления с плавающей запятой с одними и теми же данными давали разные результаты в зависимости от производителя и часто от модели компьютера.
Во многих случаях ошибки округления и усечения вычислений с фиксированной запятой легче анализировать, чем ошибки эквивалентных вычислений с плавающей запятой. С другой стороны, использование фиксированной точки требует от программиста большей осторожности. Для предотвращения переполнения требуются более точные оценки диапазонов переменных и всех промежуточных значений в вычислениях, а также часто дополнительный код для настройки их коэффициентов масштабирования.
Приложения
Операции
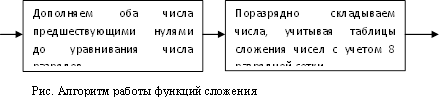
Сложение и вычитание
Умножение
Чтобы умножить два числа с фиксированной точкой, достаточно умножить два базовых целых числа и предположить, что коэффициент масштабирования результата является произведением их коэффициентов масштабирования. Результат будет точным, без округления, при условии, что он не переполняет принимающую переменную.
Разделение
Чтобы разделить два числа с фиксированной запятой, берется целое частное их базовых целых чисел и предполагается, что коэффициент масштабирования является частным их коэффициентов масштабирования. Как правило, первое деление требует округления, поэтому результат не точный.
Например, деление 3456, масштабированного на 1/100 (34,56), и 1234, масштабированного на 1/1000 (1,234), дает целое число 3456 ÷ 1234 = 3 (округлено) с коэффициентом масштабирования (1/100) / (1/1000) = 10, то есть 30. В качестве другого примера, деление первого числа на 155, неявно масштабированное на 1/32 (155/32 = 4,84375), дает целое число 3456 ÷ 155 = 22 (округлено) с неявным коэффициентом масштабирования (1 / 100) / (1/32) = 32/100 = 8/25, то есть 22 × 32/100 = 7,04.
Если результат не точен, ошибку, вносимую округлением, можно уменьшить или даже устранить путем преобразования делимого в меньший коэффициент масштабирования. Например, если r = 1,23 представлено как 123 с масштабированием 1/100, а s = 6,25 представлено как 6250 с масштабированием 1/1000, то простое деление целых чисел дает 123 ÷ 6250 = 0 (округлено) с коэффициентом масштабирования ( 1/100) / (1/1000) = 10. Если r сначала преобразовать в 1,230,000 с коэффициентом масштабирования 1/1000000, результат будет 1,230,000 ÷ 625 = 197 (округлено) с коэффициентом масштабирования 1/1000 (0,197). Точное значение 1,23 / 6,25 составляет 0,1968.
Масштабирование преобразования
При вычислениях с фиксированной точкой часто необходимо преобразовать значение в другой коэффициент масштабирования. Эта операция необходима, например:
Например, если общий коэффициент масштабирования равен 1/100, умножение 1,23 на 0,25 влечет за собой умножение 123 на 25, чтобы получить 3075 с промежуточным коэффициентом масштабирования 1/10000. Чтобы вернуться к исходному коэффициенту масштабирования 1/100, целое число 3075 затем необходимо умножить на 1/100, то есть разделить на 100, чтобы получить либо 31 (0,31), либо 30 (0,30), в зависимости от политики округления. использовал.
Преобразование в числа с плавающей точкой и обратно
Аппаратная поддержка
Масштабирование и перенормировка
Ранние компьютеры, такие как IBM 1620 и Burroughs B3500, использовали двоично-десятичное представление (BCD) для целых чисел, а именно основание 10, где каждая десятичная цифра независимо кодировалась 4 битами. Некоторые процессоры, например микроконтроллеры, все еще могут его использовать. В таких машинах преобразование десятичных коэффициентов масштабирования может выполняться битовыми сдвигами и / или манипулированием адресами памяти.
Переполнение
Переполнение происходит, когда результат арифметической операции слишком велик для сохранения в назначенной области назначения. Помимо сложения и вычитания для результата может потребоваться на один бит больше, чем для операндов. При умножении двух целых чисел без знака на m и n бит результат может иметь m + n бит.
Некоторые процессоры могут устанавливать флаг аппаратного переполнения и / или генерировать исключение при возникновении переполнения. Некоторые процессоры вместо этого могут обеспечивать арифметику насыщения : если результат сложения или вычитания был переполнен, они вместо этого сохраняют значение с наибольшей величиной, которая может поместиться в области приема и имеет правильный знак.
Однако на практике эти функции не очень полезны; Как правило, проще и безопаснее выбирать коэффициенты масштабирования и размеры слов, чтобы исключить возможность переполнения, или проверять операнды на наличие чрезмерных значений перед выполнением операции.
Компьютерная языковая поддержка
С другой стороны, все реляционные базы данных и нотация SQL поддерживают десятичную арифметику с фиксированной точкой и хранение чисел. PostgreSQL имеет специальный числовой тип для точного хранения чисел до 1000 цифр.
Более того, в 2008 году Международная организация по стандартизации (ISO) выпустила предложение о расширении языка программирования C с помощью типов данных с фиксированной точкой в интересах программ, работающих на встроенных процессорах. Кроме того, коллекция компиляторов GNU (GCC) имеет внутреннюю поддержку фиксированной точки.
Подробные примеры
Десятичное умножение с фиксированной точкой
Предположим, есть следующее умножение с двумя числами с фиксированной запятой и тремя десятичными знаками.
(10,500) (1,050) = 1 * 10,500 + 0,050 * 10,500 = 10,500 + 0,525000 = 11,025000
Таким образом, наше умножение становится
Это округляется до 11,023 с тремя цифрами после десятичной точки.
Двоичное умножение с фиксированной точкой
Для более сложного примера предположим, что два числа 1.2 и 5.6 представлены в 32-битном формате с фиксированной точкой с 30 и 20 дробными битами соответственно. Масштабирование на 2 30 и 2 20 дает 1 288 490 188,8 и 5 872 025,6, округляя до 1 288 490 189 и 5 872 026 соответственно. Оба числа по-прежнему помещаются в 32-битную целочисленную переменную со знаком и представляют собой дроби.
1. 200 000 000 186 264 514 923 095 703 125 и 5. 600 000 381 469 726 562 50
6. 720 000 458 806 753 229 623 609 513 510
Обозначения
Для краткого определения параметров формата с фиксированной точкой использовались различные обозначения. В следующем списке f представляет количество дробных битов, m количество величин или целочисленных битов, s количество знаковых битов и b общее количество битов.
Способы представления данных
Формы с плавающей и фиксированной точкой
Существует 2 способа предcтавления чисел: с плавающей и фиксированной точкой.







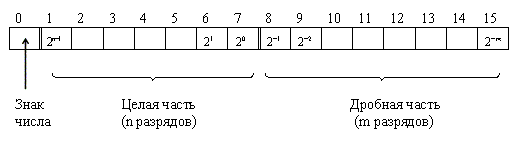
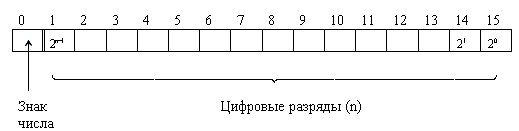
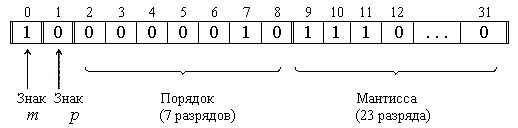
 (1·2 127 )10.
(1·2 127 )10.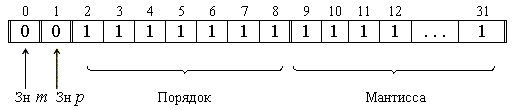
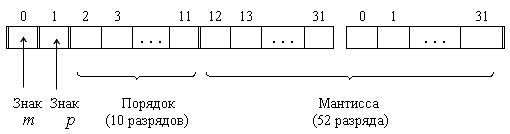
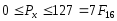
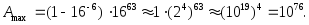
 обозначает равенство чисел в разных системах счисления):
обозначает равенство чисел в разных системах счисления):