двоичный код таблица цифр

Системы счисления. Позиционная система счисления двоичная.

Впервые позиционная система счисления возникла в древнем Вавилоне. В Индии система работает в виде

позиционной десятичной нумерации с использованием нуля, у индусов данную систему чисел

позаимствовала арабская нация, у них, в свою очередь, взяли европейцы. В Европе эту систему стали

Позиционная система — значение всех цифр зависит от позиции (разряда) данной цифры в числе.

Примеры, стандартная 10-я система счисления – это позиционная система. Допустим дано число 453.

Цифра 4 обозначает сотни и соответствует числу 400, 5 — кол-во десятков и соответствует значению 50,

а 3 — единицы и значению 3. Легко заметить, что с увеличением разряда увеличивается значение.

Таким образом, заданное число запишем в виде суммы 400+50+3=453.

Двоичная система счисления.

Во всех разрядах возможна лишь одна цифра — или нуль, или единица.

С помощью двоичной системы счисления возможно закодировать всякое натуральное число, представив

это число в виде последовательности нулей и единиц.

Пример: 10112 = 1*2 3 + 0*2*2+1*2 1 +1*2 0 =1*8 + 1*2+1=1110

Двоичную систему счисления, как и десятичную систему счисления, зачастую используют в вычислительной

технике. Текст и числа компьютер хранит в своей памяти в двоичном коде и программным способом преобразует

в изображение на экране.

Сложение, вычитание и умножение двоичных чисел.

Таблица сложения в двоичной системе счисления:

Таблица вычитания в двоичной системе счисления:

Таблица умножения в двоичной системе счисления:

Преобразование чисел в двоичной системе счисления.

Для преобразования из двоичной системы в десятичную пользуются следующей таблицей степеней

Начиная с цифры один каждая цифра умножается на 2. Точка, стоящая после 1, называют двоичной точкой.

Преобразование двоичных чисел в десятичные.

Пусть, есть двоичное число 110001₂. Для перевода в десятичное записываем его в виде суммы по

разрядам следующим образом:

1 * 2 5 + 1 * 2 4 + 0 * 2 3 + 0 * 2 2 + 0 * 2 1 + 1 * 2 0 = 49

Немного по другому:

1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 49

Также хорошо записывать расчет как таблицу:

Двигаемся справа налево. Под всеми двоичными единицами записываем её эквивалент строчкой ниже.

Далее складываем десятичные числа, которые мы получили. Т.о., двоичное число 110001₂ = десятичному 49₁₀.

Преобразование дробных двоичных чисел в десятичные.

Задание: перевести число 1011010, 101₂ в десятичную систему.

Записываем заданное число в таком виде:

Другой вариант записи:

Либо в виде таблицы:

Преобразование десятичных чисел в двоичные.

Пусть, необходимо перевести число 19 в двоичное. Можем сдеать это таким образом:

То есть, каждое частное делится на 2 и записывается остаток в конец двоичной записи. Деление

продолжается до того момента, когда в частном не будет нуля. Итог пишем справа налево. Т.е. нижняя

цифра (1) будет крайней левой и так далее. Итак, у нас получилось число 19 в двоичной записи: 10011.

Преобразование дробных десятичных чисел в двоичные.

Когда в заданном числе присутствует целая часть, то ее преобразуют отдельно от дробной. Перевод

дробного числа из десятичной системы счисления в двоичную происходит следующим образом:

разряда числа в двоичной системе счисления;

достигнута требуемая точность вычислений. В противном случае вычисления продолжаются над

дробной частью произведения.

Пример: Нужно перевести дробное десятичное число 206,116 в дробное двоичное число.

Переведя целую часть, получаем 206₁₀=11001110₂. Дробная часть 0,116 умножается на основание 2,

заносим целые части произведения в разряды после запятой:

Источник

Двоичная система счисления

Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.

Немного истории

Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.

Таблица и алфавит

Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.

100110₂ = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 38₁₀

Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:

Делимое	38	19	9	4	2
Делитель	2	2	2	2	2
Частное	19	9	4	2	1
Остаток	0	1	1	0	0

Для перевода в другие системы необходимо:

Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:

Двоичная	Восьмеричная	Шестнадцатеричная
0	0	0
001	1	1
010	2	2
011	3	3
100	4	4
101	5	5
110	6	6
111	7	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

11001001₂ = 11 001 001 = 011 001 001 = 311₈

11001001₂ = 1100 1001 = С9₁₆

Представление двоичных чисел

В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.

Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.

Прямой код предполагает приписывание единицы в начале без изменений записи:

A > 0	Aпр = 0A	1010112; Aпр = 01010112
A ≤ 0	Aпр = 1|A|	-1010112; Aпр = 11010112

Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:

A > 0	Aобр = 0A	1010112; Aобр = 01010112
A ≤ 0	Aобр = 1 A	-1010112; Aобр = 10101002

Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:

A > 0	Aдоп = 0A	1010112; Aдоп = 01010112
A ≤ 0	Aдоп = 1 A + 1	-1010112; Aдоп = 10101012

Применение двоичной системы в информатике

Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.

Источник

Двоичный код

Двоичный код — это способ представления данных в одном разряде в виде комбинации двух знаков, обычно обозначаемых цифрами 0 и 1. Разряд в этом случае называется двоичным разрядом.
В случае обозначения цифрами «0» и «1», возможные состояния двоичного разряда наделяются качественным соотношением «1» > «0» и количественными значениями чисел «0» и «1».

Двоичный код может быть непозиционным и позиционным.

Из комбинаторики известно, что, в случае непозиционного кода, количество комбинаций (кодов) n-разрядного кода является числом сочетаний с повторениями, равно биномиальному коэффициенту:

, [возможных состояний (кодов)], где:

— количество элементов в данном множестве различных элементов (количество возможных состояний, цифр, кодов в разряде),
— количество элементов в наборе (количество разрядов).
В двоичной системе кодирования (n=2) количество возможных состояний (кодов) равно :

, [возможных состояний (кодов)], т.е.

, [возможных состояний (кодов)], где

— количество двоичных разрядов (дворов, битов).
Например, в одном 8-ми битном байте (k=8) количество возможных состояний (кодов) равно:

, [возможных состояний (кодов)].

В случае позиционного кода, число комбинаций (кодов) n-разрядного двоичного кода равно числу размещений с повторениями:

, где

— число разрядов двоичного кода.

Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.
При увеличении разрядности позиционного двоичного кода на 1, количество различных комбинаций в позиционном двоичном коде удваивается.

Двоичные коды являются комбинациями двух элементов и не являются двоичной системой счисления, но используются в ней как основа. Двоичный код также может использоваться для кодирования чисел в системах счисления с любым другим основанием. Пример: в двоично-десятичном кодировании (BCD) используется двоичный код для кодирования чисел в десятичной системе счисления.
При кодировании алфавитноцифровых символов (знаков) двоичному коду не приписываются весовые коэффициенты, как это делается в системах счисления, в которых двоичный код используется для представления чисел, а используется только порядковый номер кода из множества размещений с повторениями.

В системах счисления n-разрядный двоичный код, (n-1)-разрядный двоичный код, (n-2)-разрядный двоичный код и т. д. могут отображать одно и то же число. Например, 0001, 001, 01, 1 — одно и то же число — «1» в двоичных кодах с разным числом разрядов — n.

Содержание

Таблица двоичных кодов

00000100012001030011401005010160110701118100091001A1010B1011C1100D1101E1110F1111

Пример «доисторического» использования кодов

Инки имели свою счётную систему кипу, которая физически представляла собой верёвочные сплетения и узелки. Генри Эртан обнаружил, что в узелках заложен некий код, более всего похожий на двоичную систему счисления. [1]

Примечания

См. также

Полезное

Смотреть что такое «Двоичный код» в других словарях:

двоичный код — Код, основание которого равно двум. [Сборник рекомендуемых терминов. Выпуск 94. Теория передачи информации. Академия наук СССР. Комитет технической терминологии. 1979 г.] Тематики теория передачи информации EN binary code … Справочник технического переводчика

двоичный код — dvejetainis kodas statusas T sritis automatika atitikmenys: angl. binary code vok. binärer Kode, m; Binärkode, m; dualer Kode, m; Dualkode, m rus. двоичный код, m pranc. code binaire, m … Automatikos terminų žodynas

двоичный код — Код, основание которого равно двум … Политехнический терминологический толковый словарь

двоичный код с исправлением ошибок — Двоичный код, избыточность которого обеспечивает автоматическое обнаружение и исправление ошибок некоторых типов в передаваемых данных. [Домарев В.В. Безопасность информационных технологий. Системный подход.] Тематики защита информации EN вinаry… … Справочник технического переводчика

двоичный код с обнаружением ошибок — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN binary error detecting code … Справочник технического переводчика

Двоичный код Голея — У этого термина существуют и другие значения, см. Код Голея. Двоичный код Голея один из двух тесно связанных друг с другом исправляющих ошибки линейных кодов: совершенный двоичный код Голея (англ. perfect binary Golay code) … … Википедия

арифметический двоичный код — обычный двоичный код — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы обычный двоичный код EN natural binary code … Справочник технического переводчика

натуральный двоичный код ИКМ — Код, при котором кодовые слова, соответствующие квантованным отсчетам сигнала электросвязи при ИКМ, расположенным в порядке возрастания амплитуд, представляют собой неотрицательные целые двоичные числа, взятые в том же порядке. [ГОСТ 22670 77]… … Справочник технического переводчика

сбалансированный двоичный код — код без преобладания — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы код без преобладания EN zero disparity code … Справочник технического переводчика

симметричный двоичный код ИКМ — Код, при котором полярность квантованного отсчета сигнала электросвязи при ИКМ выражается одним символом цифрового сигнала электросвязи, а остальные символы выражают двоичное число, представляющее абсолютную величину отсчета этого сигнала.… … Справочник технического переводчика

Источник

Двоичный код.

Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.

Видя что-то впервые, мы зачастую задаемся логичным вопросом о том, как это работает. Любая новая информация воспринимается нами, как что-то сложное или созданное исключительно для разглядываний издали, однако для людей, желающих узнать подробнее о двоичном коде, открывается незамысловатая истина – бинарный код вовсе не сложный для понимания, как нам кажется. К примеру, английская буква T в двоичной системе приобретет такой вид – 01010100, E – 01000101 и буква X – 01011000. Исходя из этого, понимаем, что английское слово TEXT в виде двоичного кода будет выглядеть таким вот образом: 01010100 01000101 01011000 01010100. Компьютер понимает именно такое изложение символов для данного слова, ну а мы предпочитаем видеть его в изложении букв алфавита.

На сегодняшний день двоичный код активно используется в программировании, поскольку работают вычислительные машины именно благодаря ему. Но программирование не свелось до бесконечного набора нулей и единиц. Поскольку это достаточно трудоемкий процесс, были приняты меры для упрощения понимания между компьютером и человеком. Решением проблемы послужило создание языков программирования (бейсик, си++ и т.п.). В итоге программист пишет программу на языке, который он понимает, а потом программа-компилятор переводит все в машинный код, запуская работу компьютера.

Перевод натурального числа десятичной системы счисления в двоичную систему.

Чтобы перевести числа из десятичной системы счисления в двоичную пользуются «алгоритмом замещения», состоящим из такой последовательности действий:

1. Выбираем нужное число и делим его на 2. Если результат деления получился с остатком, то число двоичного кода будет 1, если остатка нет – 0.

2. Откидывая остаток, если он есть, снова делим число, полученное в результате первого деления, на 2. Устанавливаем число двоичной системы в зависимости от наличия остатка.

3. Продолжаем делить, вычисляя число двоичной системы из остатка, до тех пор, пока не дойдем до числа, которое делить нельзя – 0.

4. В этот момент считается, что двоичный код готов.

Для примера переведем в двоичную систему число 7:

1. 7 : 2 = 3.5. Поскольку остаток есть, записываем первым числом двоичного кода 1.

2. 3 : 2 = 1.5. Повторяем процедуру с выбором числа кода между 1 и 0 в зависимости от остатка.

3. 1 : 2 = 0.5. Снова выбираем 1 по тому же принципу.

4. В результате получаем, переведенный из десятичной системы счисления в двоичную, код – 111.

Таким образом можно переводить бесконечное множество чисел. Теперь попробуем сделать наоборот – перевести число из двоичной в десятичную.

Перевод числа двоичной системы в десятичную.

Для этого нам нужно пронумеровать наше двоичное число 111 с конца, начиная нулем. Для 111 это 1^2 1^1 1^0. Исходя из этого, номер для числа послужит его степенем. Далее выполняем действия по формуле: (x * 2^y) + (x * 2^y) + (x * 2^y), где x – порядковое число двоичного кода, а y – степень этого числа. Подставляем наше двоичное число под эту формулу и считаем результат. Получаем: (1 * 2^2) + (1 * 2^1) + (1 * 2^0) = 4 + 2 + 1 = 7.

Немного из истории двоичной системы счисления.

Источник

Бинарный код

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).

Содержание

Таблица умножения двоичных чисел

Использование двоичной системы при измерении дюймами

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7 15 / 16″, 3 11 / 32″ и т. д.

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:

512	256	128	64	32	16	8	4	2	1
1	1	0	0	1	1
32	+16	+2	+1

Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо .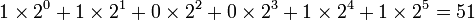

Преобразование методом Горнера

Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.

Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа

Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.

Другие системы счисления

В статье «Системы счисления (продолжение)» [1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.

См. также

Ссылки

Полезное

Смотреть что такое «Бинарный код» в других словарях:

Код Грея — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея система счисления, в которой два соседних значения… … Википедия

Пойнт-код — Код сигнальной точки (англ. Signal Point Code (SPC)) сигнальной системы 7 (SS7, ОКС 7) это уникальный (в домашней сети) адрес узла, используемый на третьем уровне MTP (маршрутизация) в телекоммуникационных ОКС 7 сетях для идентификации … Википедия

Бесквадратное число — В математике бесквадратным называется число, которое не делится ни на один квадрат, кроме 1. К примеру, 10 бесквадратное, а 18 нет, так как 18 делится на 9 = 32. Начало последовательности бесквадратных чисел таково: 1, 2, 3, 5, 6, 7,… … Википедия

Direct3D 10 — Для улучшения этой статьи желательно?: Викифицировать статью. Переработать оформление в соответствии с правилами написания статей. Исправить статью согласно стилистическим правилам Википедии … Википедия

Python — У этого термина существуют и другие значения, см. Python (значения). Python Класс языка: му … Википедия

Хакерская атака — в узком смысле слова в настоящее время под словосочетанием понимается «Покушение на систему безопасности», и склоняется скорее к смыслу следующего термина Крэкерская атака. Это произошло из за искажения смысла самого слова «хакер». Хакерская… … Википедия

Грей — (от англ. gray/grey серый) шотландская и английская фамилия. Содержание 1 Известные носители 2 Грей, как псевдоним известных людей … Википедия

Кодирование Голомба — Коды Голомба это семейство энтропийных кодеров, являющихся общим случаем унарного кода. Также под кодом Голомба может подразумеваться один из представителей этого семейства. Код Голомба позволяет представить последовательность символов в виде… … Википедия

Крэкерская атака — Хакерская атака в узком смысле слова в настоящее время под словосочетанием понимается «Покушение на систему безопасности», и склоняется скорее к смыслу следующего термина Крэкерская атака. Это произошло из за искажения смысла самого слова «хакер» … Википедия

Источник