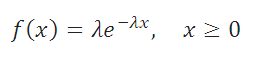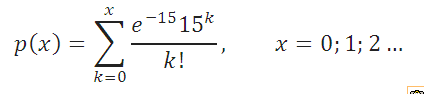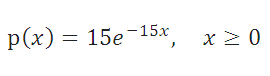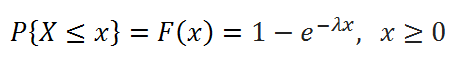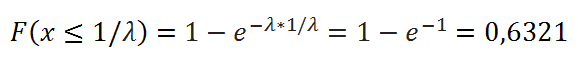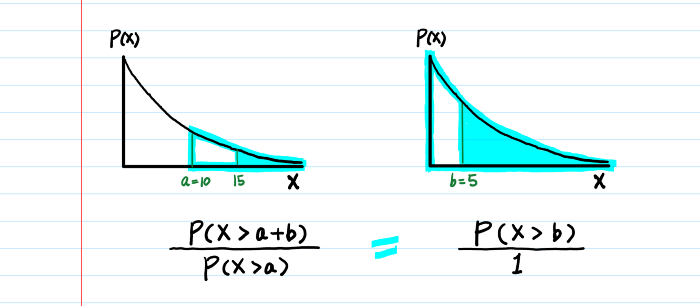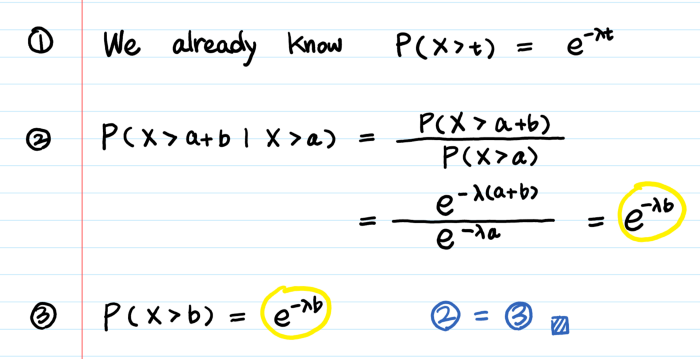экспоненциальное распределение с параметром

Экспоненциальное распределение

Oct 10, 2019 · 6 min read

Мы всегда начинаем с вопроса “почему”, прежде чем переходить к формулам. Если вы понимаете, почему что-то работает, вы с большей вероятностью будете применять это в своей работе.

1. Почему мы изобрели экспоненциальное распределение?

Ответ: чтобы получить распределение, предсказывающее периоды времени между событиями (такими как успех, отказ, доставка и так далее).

Например, мы хотим предсказать следующее:

Следующий вопрос такой: почему λ * e^(−λt) — это плотность вероятности времени до следующего события?

И следующий вопрос: что значит X

EXP(0,25)? Параметр 0,25 означает 0,25 минут, часов или дней, а, может, 0,25 событий?

Предполагается, что вы хорошо знакомы с распределением Пуассона. Если нет, эта статья поможет разобраться.

EX P (λ) ➡ Э кспоненциальный параметр λ тот же самый, что и λ в распределении Пуассона?

Важная вещь, которая позже поможет вам не запутаться с X

EXP(0,25). 0,25 — это не временной период, а число событий, совпадающее с параметром λ в процессе Пуассона.

Например, ваш блог посещают 500 пользователей в день. Это среднее значение. Количество клиентов магазина за час, землетрясений в год, автомобильных аварий в неделю, опечаток на странице и так далее — это средние значения событий (λ) в единицу времени, являющиеся параметром распределения Пуассона.

Однако при моделировании времени между событиями удобнее использовать термины времени, а не количества. Например, число лет, в течение которых компьютер может включаться без ошибок — 10 лет (это удобнее, чем говорить “ 0,1 ошибка в год”), новый покупатель приходит каждые 10 минут, крупные ураганы возникают каждые 7 лет и так далее.

Путаница возникает, когда вы видите термин “ затухание”, или еще хуже, “ скорость затухания”, которые часто используются в экспоненциальном распределении. З атухание выражается через время (каждые 10 минут, каждые 7 лет и т.д.) и является обратной величиной параметра (λ) в распределении Пуассона. Смотрите: если у вас 3 посетителя в час, значит у вас 1 посетитель каждую треть часа.

Итак, мы можем ответить на вопрос:
Что значит “X

Это означает, что параметр Пуассона будет равен 0,25. В течение единицы времени (неважно, в минутах, часах или годах) событие происходит в среднем 0,25 раз. Переводя в термины времени — пройдет 4 часа, прежде чем событие произойдет, если за единицу времени принят 1 час.

2. Вывод плотности вероятности

Наш первый вопрос был: почему λ * e^(−λt) — это плотность вероятности времени до следующего события?

Определение экспоненциального распределения — это распределение вероятности времени *между* событиями в процессе Пуассона.

Смотрите: в период ожидания не происходит ни одного события. Другими словами, Пуассон (X=0).

Есть важная вещь, которую стоит помнить о пуассоновской плотности вероятности: период времени, в течение которого возникают пуассоновские события (X=k), составляет только одну (1) единицу времени.

Как смоделировать распределение вероятности не просто в течение одной единицы времени, а “ ничего не произошло в период времени t”?

Распределение Пуассона предполагает, что события возникают независимо друг от друга. Следовательно, можно посчитать вероятность нулевого успеха в течение t единиц времени, умножив P(X=0 в единицу времени) на t раз.

Плотность вероятности — это производная от кумулятивной функции распределения вероятности.

Поскольку у нас уже есть кумулятивная функция распределения вероятности экспоненциального распределения, 1 — P(T > t), мы можем получить плотность вероятности, продифференцировав ее.

Источник

Экспоненциальное распределение. Непрерывные распределения в EXCEL

history 8 ноября 2016 г.

Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.

Экспоненциальное распределение (англ. Exponential distribution ) часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение Экспоненциального распределения :

Плотность вероятности Экспоненциального распределения задается следующей формулой:

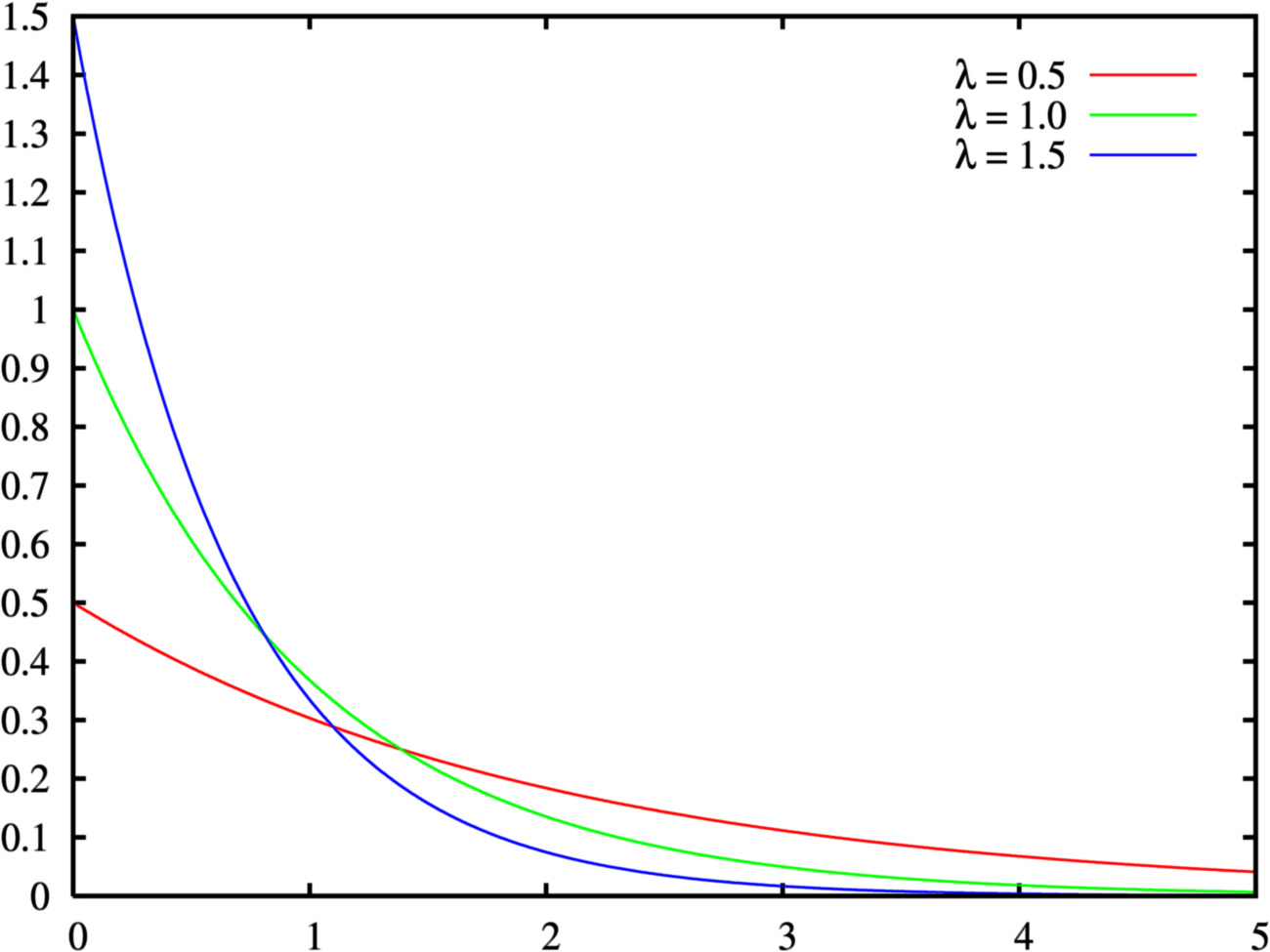
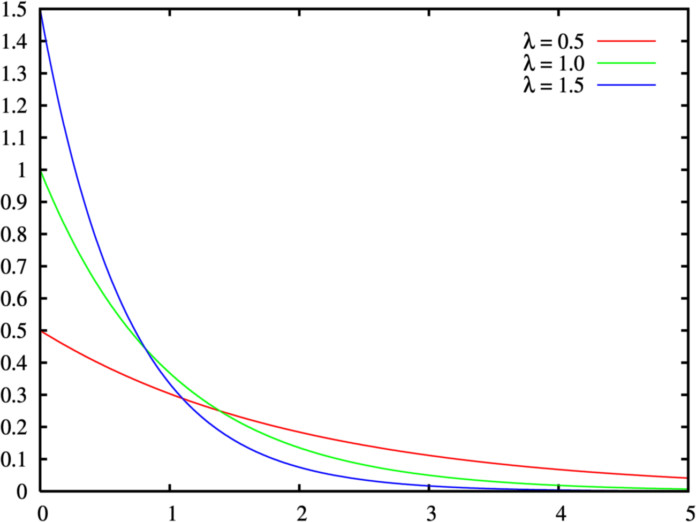
График плотности распределения вероятности и интегральной функции Экспоненциального распределения выглядит следующим образом (см. ниже).

Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается распределением Пуассона со средним значением равным 15 машин в час (параметр распределения λ =15). Вероятность того, что на стоянку в течение часа приедет k машин равно:

Экспоненциальное распределение в MS EXCEL

Экспоненциальное распределение имеет обозначение Exp ( λ ).

В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :

Графики функций

Генерация случайных чисел

Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).

Задачи

Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый Экспоненциальным распределением с интенсивностью отказа равной 10^(-3) в час, таким образом, λ = 10^(-3). Среднее время до отказа равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за Среднее время до отказа, то нужно записать формулу:

Т.е. результат не зависит от параметра λ .

В MS EXCEL решение выглядит так: =ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)

Источник

Экспоненциальное распределение

Мы всегда начинаем с вопроса “почему”, прежде чем переходить к формулам. Если вы понимаете, почему что-то работает, вы с большей вероятностью будете применять это в своей работе.

1. Почему мы изобрели экспоненциальное распределение?

Ответ: чтобы получить распределение, предсказывающее периоды времени между событиями (такими как успех, отказ, доставка и так далее).

Например, мы хотим предсказать следующее:

Следующий вопрос такой: почему λ * e^(−λt) — это плотность вероятности времени до следующего события?

И следующий вопрос: что значит X

EXP(0,25)?Параметр 0,25 означает 0,25 минут, часов или дней, а, может, 0,25 событий?

Предполагается, что вы хорошо знакомы с распределением Пуассона. Если нет, эта статья поможет разобраться.

EXP(λ) ➡ Экспоненциальный параметр λ тот же самый, что и λ в распределении Пуассона?

Важная вещь, которая позже поможет вам не запутаться с X

EXP(0,25).0,25 — это не временной период, а число событий, совпадающее с параметром λ в процессе Пуассона.

Например, ваш блог посещают 500 пользователей в день. Это среднее значение. Количество клиентов магазина за час, землетрясений в год, автомобильных аварий в неделю, опечаток на странице и так далее — это средние значения событий (λ) в единицу времени, являющиеся параметром распределения Пуассона.

Однако при моделировании времени между событиями удобнее использовать термины времени, а не количества. Например, число лет, в течение которых компьютер может включаться без ошибок — 10 лет (это удобнее, чем говорить “0,1 ошибка в год”), новый покупатель приходит каждые 10 минут, крупные ураганы возникают каждые 7 лет и так далее.

Путаница возникает, когда вы видите термин “затухание”, или еще хуже, “скорость затухания”, которые часто используются в экспоненциальном распределении. Затухание выражается через время (каждые 10 минут, каждые 7 лет и т.д.) и является обратной величиной параметра (λ) в распределении Пуассона. Смотрите: если у вас 3 посетителя в час, значит у вас 1 посетитель каждую треть часа.

Итак, мы можем ответить на вопрос:
Что значит “X

Это означает, что параметр Пуассона будет равен 0,25. В течение единицы времени (неважно, в минутах, часах или годах) событие происходит в среднем 0,25 раз. Переводя в термины времени — пройдет 4 часа, прежде чем событие произойдет, если за единицу времени принят 1 час.

2. Вывод плотности вероятности

Наш первый вопрос был: почему λ * e^(−λt) — это плотность вероятности времени до следующего события?

Определение экспоненциального распределения — это распределение вероятности времени *между* событиями в процессе Пуассона.

Смотрите: в период ожидания не происходит ни одного события. Другими словами, Пуассон (X=0).

Пуассон (X=0): первый этап экспоненциального распределения

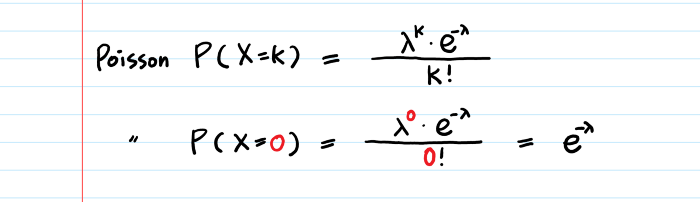
Есть важная вещь, которую стоит помнить о пуассоновской плотности вероятности: период времени, в течение которого возникают пуассоновские события (X=k), составляет только одну (1) единицу времени.

Как смоделировать распределение вероятности не просто в течение одной единицы времени, а “ничего не произошло в период времени t”?

Распределение Пуассона предполагает, что события возникают независимо друг от друга. Следовательно, можно посчитать вероятность нулевого успеха в течение t единиц времени, умножив P(X=0 в единицу времени) на t раз.

Плотность вероятности — это производная от кумулятивной функции распределения вероятности.

Поскольку у нас уже есть кумулятивная функция распределения вероятности экспоненциального распределения, 1 — P(T > t), мы можем получить плотность вероятности, продифференцировав ее.

3. Отсутствие последействия

Отсутствие последействия — полезный параметр?

Рационально ли моделировать долговечность механического устройства, используя экспоненциальное распределение?

Например, если устройство уже проработало девять лет, отсутствие последействия означает, что вероятность его бесперебойной работы в следующие три года (то есть в сумме 12 лет) точно такая же, как для совершенно нового механизма.

Это уравнение кажется вам разумным?

Мне нет. Как показывает мой опыт, чем старше устройство, тем вероятнее поломка. Смоделировать этот параметр — возрастающую интенсивность отказов — можно с помощью распределения Вейбулла.

Так когда же стоит применять экспоненциальное распределение (постоянную интенсивность отказов)?

Автомобильные происшествия. Если никто не врезался в вас за последние пять часов, это не снижает и не повышает шансы попадания в аварию.

Где еще есть отсутствие последействия?

Экспоненциальное распределение — это единственное непрерывное распределение с отсутствием последействия (или распределение с постоянной интенсивностью отказов). Геометрическое распределение, его дискретный аналог, является единственным дискретным распределением с отсутствием последействия.

a) Моделирование времени ожидания

У значений экспоненциальной случайной величины есть много маленьких значений и немного крупных значений. Автобус, который вы ждете, скорее всего приедет в течение 10 минут нежели в течение 60 минут.

Используя экспоненциальное распределение, можно ответить на следующие вопросы:

1. Автобус в среднем приезжает каждые 15 минут (предположим, что время между прибытием автобусов имеет экспоненциальное распределение, значит, количество автобусов, прибывающих в течение часа имеет распределение Пуассона). И я только что пропустила автобус! Водитель был злой. Как только я пришла, он закрыл двери и уехал. Если следующий автобус не приедет в течение десяти мнут, я вызову Uber, иначе опоздаю. Какова вероятность того, что ожидание следующего автобуса займет меньше 10 минут?

2. Девяносто процентов автобусов прибывают через сколько минут после предыдущего?

3. В течение какого времени в среднем прибывают два автобуса?

b) Моделирование отказа

Раз мы можем смоделировать успешное событие (прибытие автобуса), почему бы не смоделировать отказ — время поломки продукта.

Количество часов, которое AWS оборудование способно проработать без перезагрузки, соответствует экспоненциальному распределению со средним значением 8 000 часов в год.

1. У вас нет резервного сервера, а вам нужна бесперебойная работа в течение 10 000 часов. Какова вероятность того, что вы сможете выполнить эту задачу без перезагрузки сервера?

2. Какова вероятность того, что сервер не потребует перезагрузки между 12 и 18 месяцами?

Заметьте, что иногда экспоненциальное распределение не подходит — когда интенсивность отказов изменяется в течение срока службы. Тем не менее это единственное распределение, обладающее уникальным параметром — постоянной интенсивностью отказов.

c) Моделирование времени обслуживания (Теория очередей)

Время обслуживания (например, как долго в кафе готовят мне буррито) тоже можно смоделировать как экспоненциально распределенные переменные.

Общая длина процесса — последовательность нескольких независимых задач — соответствует распределению Эрланга: распределению суммы нескольких независимых экспоненциально распределенных переменных.

5. Вкратце: связь между экспоненциальным и пуассоновским распределениями

Если число событий в единицу времени соответствует распределению Пуассона, тогда период времени между событиями соответствует экспоненциальному распределению.

Предположим, что на период времени между событиями не влияют предыдущие события (то есть они независимы), тогда число событий в единицу времени соответствует распределению Пуассона со значением λ = 1/μ.

6. Упражнение

Как оказалось, в понимании математических тем мне помогает решение задач. Попробуйте решить задания ниже.

2. Максимальное значение плотности распределения вероятности на оси y — λ. Почему?

3. X1 и X2 — независимые экспоненциальные случайные переменные со значением λ.

Какова плотность вероятности Y?
Где может быть использовано это распределение?

Источник

Исследуем утверждение центральной предельной теоремы с помощью экспоненциального распределения

Вместо введения

В статье описывается исследование, проведенное с целью проверки утверждения центральной предельной теоремы о том, что сумма N независимых и одинаково распределенных случайных величин, отобранных практически из любого распределения, имеет распределение, близкое к нормальному. Однако, прежде чем мы перейдем к описанию исследования и более подробному раскрытию смысла центральной предельной теоремы, не лишним будет сообщить, зачем вообще проводилось исследование и кому может быть полезна статья.

В первую очередь, статья может быть полезна всем начинающим постигать основы машинного обучения, в особенности если уважаемый читатель еще и на первом курсе специализации «Машинное обучение и анализ данных». Именно подобного рода исследование требуется провести на заключительной неделе первого курса, указанной выше специализации, чтобы получить заветный сертификат.

Подход к проведению исследования

Итак, вернемся к вопросу исследования. О чем говорит нам центральная предельная теорема. А говорит она вот о чем. Если есть случайная величина X из практически любого распределения, и из этого распределения случайным образом сформирована выборка объемом N, то выборочное среднее, определенное на основании выборки, можно приблизить нормальным распределением со средним значением, которое совпадает с математическим ожиданием исходной совокупности.

Для проведения эксперимента нам потребуется выбрать распределение, из которого случайным образом будет формироваться выборка. В нашем случае мы воспользуемся экспоненциальным распределением.

Итак, мы знаем, что плотность вероятности экспоненциального распределения случайной величины X имеет вид:

, где 0$» data-tex=»inline»/>, 0$» data-tex=»inline»/>

Математическое ожидание случайной величины X, в соответствии с законом экспоненциального распределения определяется, обратно :

Дисперсия случайной величины X определяется как

В нашем исследовании используется параметр экспоненциального распределения , тогда ,

Для упрощения восприятия значений и самого эксперимента, предположим, что речь идет о работе устройства со средним ожиданием времени безотказной работы в 80 часов. Тогда, чем больше времени проработает устройство, тем меньше вероятности того, что не будет отказа и наоборот – при стремлении работы устройства к нулю времени (часам, минутам, секундам), вероятность его поломки также стремится к нулю.

Теперь из экспоненциального распределения с заданным параметром выберем 1000 псевдослучайных значений. Сравним полученные результаты выборки с теоретической плотностью вероятности.

Далее, и это самое главное в нашем небольшом исследовании, сформируем следующие выборки. Возьмем 3, 15, 50, 100, 150, 300 и 500 случайных величин из экспоненциального распределения, определим для каждого объема (от 3 до 500) среднее арифметическое, повторим 1000 раз. Для каждой выборки построим гистограмму и наложим на нее график плотности соответствующего нормального распределения. Оценим получившиеся параметры выборочного среднего, дисперсии и стандартного отклонения.

На этом можно было бы завершить статью, но есть предложение несколько расширить границы эксперимента. Оценим насколько указанные параметры, при увеличении объема выборки от 3 до 500, будут отличаться от своих собратьев – таких же параметров соответствующих нормальных распределений. Другими словами, нам предлагается ответить на вопрос, а будем ли мы наблюдать уменьшение отклонений при увеличении объема выборки?

Итак, в путь. Нашими инструментами сегодня будут язык Python и Jupyter notebook.

Исследуем утверждение центральной предельной теоремы

Исходный код исследования выложен на гитхабе
Внимание! Для работы с файлом требуется Jupyter notebook!

Сгенерированная нами в соответствии с законом экспоненциального распределения выборка псевдослучайной величины 1000 раз достаточно хорошо характеризует теоретическую (исходную) совокупность (график 1*, таблица 1).

График 1 «Исходная совокупность экспоненциального распределения и выборка»

Таблица 1 «Параметры исходной совокупности и выборки»

Теперь посмотрим, что произойдет, если мы возьмем 1000 раз не одну псевдослучайную величину, а среднее арифметическое от 3, 15, 50, 100, 150, 300 или 500 псевдослучайных величин и сравним параметры каждой выборки с параметрами соответствующих нормальных распределений (график 2**, таблица 2).

График 2.1 «Выборка объемом 5»


График 2.2 «Выборка объемом 50»


График 2.3 «Выборка объемом 100»


График 2.4 «Выборка объемом 150»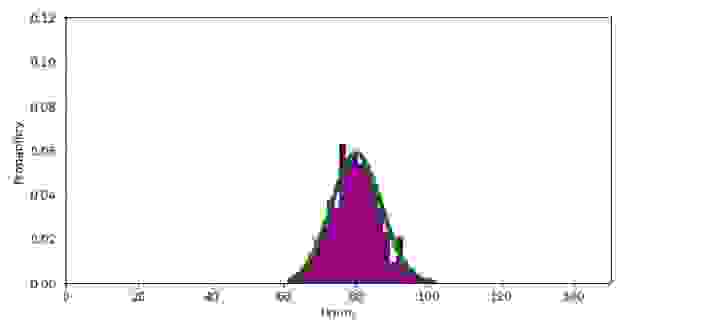


График 2.5 «Выборка объемом 300»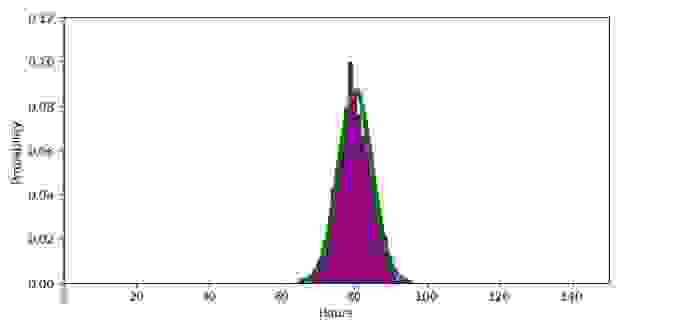


График 2.6 «Выборка объемом 500»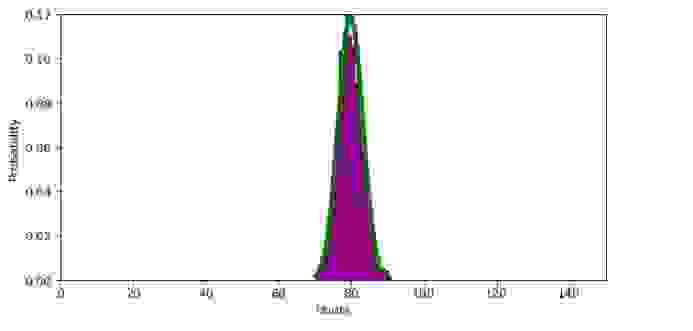


Таблица 2 «Параметры выборок»

В соответствии с графическим представлением результатов хорошо прослеживается следующая закономерность: с ростом объема выборки распределение приближается к нормальному и происходит концентрация псевдослучайных величин вокруг выборочного среднего, а выборочное среднее приближается к математическому ожиданию исходного распределения.

В соответствии с данными представленными в таблице, подтверждается закономерность, выявленная на графиках – с ростом объема выборки, значения дисперсий и стандартных отклонений заметно снижаются, что указывает на более плотную концентрацию псевдослучайных величин вокруг выборочных средних.

Но это, еще не все. Мы помним, что в начале статьи было сформировано предложение проверить будут ли с ростом объема выборки уменьшаться отклонения параметров выборки относительно параметров соответствующего нормального распределения.

Как видно (график 3, таблица 3), сколь угодно заметного сокращения отклонений не происходит – параметры выборок прыгают то в плюс, то в минус на разные расстояния и никак не хотят стабильно приближаться к расчетным значениям. Объяснение отсутствия положительной динамики мы обязательно попытаемся найти в следующих исследованиях.

График 3 «Отклонения параметров выборок от расчетных теоретических»

Таблица 3 «Отклонения параметров выборок от расчетных теоретических»

Вместо выводов

Наше исследование, с одной стороны, в очередной раз, подтвердило выводы центральной предельной теоремы о приближении независимых случайно распределенных величин к нормальному распределению с ростом объема выборки, с другой стороны, позволило успешно завершить обучение первого курса большой специализации.

* Развивая логику примера с оборудованием, безотказное время которого составляет 80 часов, по оси «икс» мы обозначим часы – чем меньше времени работает, тем меньше вероятности отказа.

** Здесь требуется иная интерпретация значений по оси «икс» — вероятность того, что прибор отработает в около 80 часов самая высокая и соответственно она уменьшается как при увеличении времени работы (то есть маловероятно, что прибор будет работать намного дольше 80-ти часов), так и при уменьшении времени работы (вероятность того, что прибор выйдет из строя менее чем за 80-ть часов также мала).

Следующая работа автора — «Решаем уравнение простой линейной регрессии»

Источник