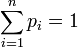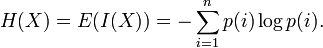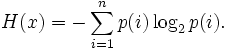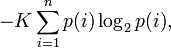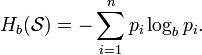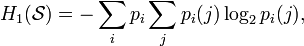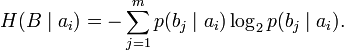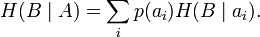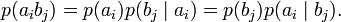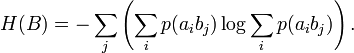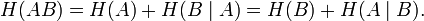энтропия это параметр оценивающий в информатике
Что такое энтропия файла
Любой компьютерный файл, как известно, состоит из байтов. Байт может принимать значения от 0 до 255. Информационная энтропия – это статистический параметр, который показывает вероятность встречаемости определённых байтов в файле.
Визуально оценить степень энтропии можно с помощью гистограммы – распределения вероятности повторов одинаковых байтов в файле. По энтропии файла можно предположить, какого типа файл перед нами, видя только его гистограмму.
Для демонстрации возьмём три файла разных типов и сравним их гистограммы.
Гистограмма текстового файла
Первый пусть будет текстовый файл (*.TXT). Его гистограмма показана на рисунке:

Текстовый файл содержит только текст. Каждый символ текста кодируется определёнными байтами в соответствии с таблицей кодировки. Хотя видов кодировок достаточно большое количество, представленный файл – в кодировке ASCII, поэтому на первой гистограмме заняты лишь некоторые области, а больше числа 127 значений нет вовсе (127 – предельный код символа в таблице ASCII). Видно, что некоторые из символов (букв или цифр) в файле встречаются чаще, некоторые – реже. Больше всего в текстовом файле пробелов, отсюда и высокий пик на значении байта 3210.
Гистограмма PDF файла
Следующий файл будет формата PDF:

Этот файл имеет все возможные байты, так как формат PDF кодируется не так, как текстовые файлы. Он хранит много служебной информации: форматирование, шрифты, изображения и т.д. Но по его гистограмме видно, что некоторые из байтов встречаются с примерно равной вероятностью, в то время как другие – намного чаще остальных. Отсюда и множественные острые всплески на гистограмме, и в целом она имеет довольно «рваный» вид, хотя и занимает всю доступную ширину.
Гистограмма архива 7Z
И последний файл – заархивированный в формат 7Z:

Гистограмма архива 7Z имеет две основные особенности: во-первых, все байты встречаются в заархивированном файле с более-менее равной вероятностью (достаточно ровный верхний край), а во-вторых, практически отсутствует свободное пространство над гистограммой, что говорит о почти полном отсутствии избыточности такого файла. Отсюда можно сделать вывод, что алгоритм архиватора каким-то особым образом «перемешивает» байты файла, чтобы добиться их максимально равномерного распределения.
Таким образом, энтропия в информатике, как и в физике – это мера неупорядоченности системы, в данном случае – неупорядоченности распределения байтов в файле. Энтропия позволяет судить о степени сжатия файла и – косвенно – о его типе.
Программа визуализации энтропии файлов
Энтропия (теория информации)
Энтропи́я (информационная) — мера хаотичности информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения.
Для иллюстрации понятия информационной энтропии можно также прибегнуть к примеру из области термодинамической энтропии, получившему название демона Максвелла. Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу.
Содержание
Формальные определения
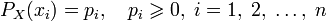
Тогда энтропия будет определяться как:
От основания логарифма зависит единица измерения информации и энтропии: бит, нат или хартли.
Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n ) рассчитывается по формуле:
Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:
Шеннон показал, что единственная функция, удовлетворяющая этим требованиям, имеет вид:
где K — константа (и в действительности нужна только для выбора единиц измерения).
Шеннон определил, что измерение энтропии (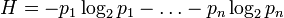
Определение энтропии Шеннона связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между термодинамической и информационной энтропией. Например, демон Максвелла также противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии.
Альтернативное определение
Другим способом определения функции энтропии H является доказательство, что H однозначно определена (как указано ранее), если и только если H удовлетворяет условиям:
Свойства
Важно помнить, что энтропия является количеством, определённым в контексте вероятностной модели для источника данных. Например, кидание монеты имеет энтропию − 2(0,5log20,5) = 1 бит на одно кидание (при условии его независимости). У источника, который генерирует строку, состоящую только из букв «А», энтропия равна нулю: 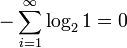
Математические свойства
Эффективность
Исходный алфавит, встречающийся на практике, имеет вероятностное распределение, которое далеко от оптимального. Если исходный алфавит имел n символов, тогда он может быть сравнён с «оптимизированным алфавитом», вероятностное распределение которого однородно. Соотношение энтропии исходного и оптимизированного алфавита — это эффективность исходного алфавита, которая может быть выражена в процентах.
Энтропия ограничивает максимально возможное сжатие без потерь (или почти без потерь), которое может быть реализовано при использовании теоретически — типичного набора или, на практике, — кодирования Хаффмана, кодирования Лемпеля — Зива — Велча или арифметического кодирования.
Вариации и обобщения
Условная энтропия
Если следование символов алфавита не независимо (например, во французском языке после буквы «q» почти всегда следует «u», а после слова «передовик» в советских газетах обычно следовало слово «производства» или «труда»), количество информации, которую несёт последовательность таких символов (а следовательно и энтропия) очевидно меньше. Для учёта таких фактов используется условная энтропия.
Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (то есть вероятности двухбуквенных сочетаний):
Так, для русского языка без буквы «ё» 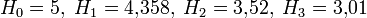
| b1 | b2 | … | bj | … | bm | |
|---|---|---|---|---|---|---|
| a1 | 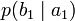 | 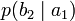 | … | 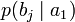 | … | 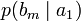 |
| a2 | 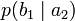 | 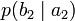 | … | 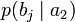 | … | 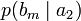 |
| … | … | … | … | … | … | … |
| ai | 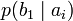 | 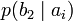 | … | 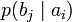 | … | 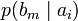 |
| … | … | … | … | … | … | … |
| am | 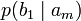 | 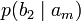 | … | 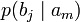 | … | 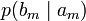 |
Для вычисления потерь при передаче всех сигналов используется общая условная энтропия:
Взаимная энтропия
| p(a1b1) | p(a1b2) | … | p(a1bj) | … | p(a1bm) |
| p(a2b1) | p(a2b2) | … | p(a2bj) | … | p(a2bm) |
| … | … | … | … | … | … |
| p(aib1) | p(aib2) | … | p(aibj) | … | p(aibm) |
| … | … | … | … | … | … |
| p(amb1) | p(amb2) | … | p(ambj) | … | p(ambm) |
Условные вероятности производятся по формуле Байеса. Таким образом имеются все данные для вычисления энтропий источника и приёмника:
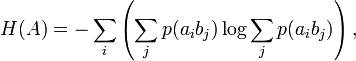
Взаимная энтропия вычисляется последовательным суммированием по строкам (или по столбцам) всех вероятностей матрицы, умноженных на их логарифм:
| H(AB) = − | ∑ | ∑ | p(aibj)logp(aibj). |
| i | j |
Единица измерения — бит/два символа, это объясняется тем, что взаимная энтропия описывает неопределённость на пару символов — отправленного и полученного. Путём несложных преобразований также получаем
Взаимная энтропия обладает свойством информационной полноты — из неё можно получить все рассматриваемые величины.
История
В 1948 году, исследуя проблему рациональной передачи информации через зашумлённый коммуникационный канал, Клод Шеннон предложил революционный вероятностный подход к пониманию коммуникаций и создал первую, истинно математическую, теорию энтропии. Его сенсационные идеи быстро послужили основой разработки двух основных направлений: теории информации, которая использует понятие вероятности и эргодическую теорию для изучения статистических характеристик данных и коммуникационных систем, и теории кодирования, в которой используются главным образом алгебраические и геометрические инструменты для разработки эффективных кодов.
Понятие энтропии, как меры случайности, введено Шенноном в его статье «A Mathematical Theory of Communication», опубликованной в двух частях в Bell System Technical Journal в 1948 году.
Бит, информационная энтропия Шеннона и код Хэмминга. Как измерить любую информацию и передать ее без потерь
«Информация есть форма жизни», — писал американский поэт и эссеист Джон Перри Барлоу. Действительно, мы постоянно сталкиваемся со словом «информация» — ее получают, передают и сохраняют. Узнать прогноз погоды или результат футбольного матча, содержание фильма или книги, поговорить по телефону — всегда ясно, с каким видом информации мы имеем дело. Но что такое сама информация, а главное — как ее можно измерить, никто обычно не задумывается. А между тем, информация и способы ее передачи — важная вещь, которая во многом определяет нашу жизнь, неотъемлемой частью которой стали информационные технологии. Научный редактор издания «Лаба.Медиа» Владимир Губайловский объясняет, что такое информация, как ее измерять, и почему самое сложное — это передача информации без искажений.
Читайте «Хайтек» в
Пространство случайных событий
В 1946 году американский ученый-статистик Джон Тьюки предложил название БИТ (BIT, BInary digiT — «двоичное число» — «Хайтек») — одно из главных понятий XX века. Тьюки избрал бит для обозначения одного двоичного разряда, способного принимать значение 0 или 1. Клод Шеннон в своей программной статье «Математическая теория связи» предложил измерять в битах количество информации. Но это не единственное понятие, введенное и исследованное Шенноном в его статье.
Представим себе пространство случайных событий, которое состоит из бросания одной фальшивой монеты, на обеих сторонах которой орел. Когда выпадает орел? Ясно, что всегда. Это мы знаем заранее, поскольку так устроено наше пространство. Выпадение орла — достоверное событие, то есть его вероятность равна 1. Много ли информации мы сообщим, если скажем о выпавшем орле? Нет. Количество информации в таком сообщении мы будем считать равным 0.
Теперь давайте бросать правильную монету: с одной стороны у нее орел, а с другой решка, как и положено. Выпадение орла или решки будут двумя разными событиями, из которых состоит наше пространство случайных событий. Если мы сообщим об исходе одного бросания, то это действительно будет новая информация. При выпадении орла мы сообщим 0, а при решке 1. Для того, чтобы сообщить эту информацию, нам достаточно 1 бита.
Что изменилось? В нашем пространстве событий появилась неопределенность. Нам есть, что о нем рассказать тому, кто сам монету не бросает и исхода бросания не видит. Но чтобы правильно понять наше сообщение, он должен точно знать, чем мы занимаемся, что означают 0 и 1. Наши пространства событий должны совпадать, и процесс декодирования — однозначно восстанавливать результат бросания. Если пространство событий у передающего и принимающего не совпадает или нет возможности однозначного декодирования сообщения, информация останется только шумом в канале связи.
Если независимо и одновременно бросать две монеты, то разных равновероятных результатов будет уже четыре: орел-орел, орел-решка, решка-орел и решка-решка. Чтобы передать информацию, нам понадобится уже 2 бита, и наши сообщения будут такими: 00, 01, 10 и 11. Информации стало в два раза больше. Это произошло, потому что выросла неопределенность. Если мы попытаемся угадать исход такого парного бросания, то имеем в два раза больше шансов ошибиться.
Чем больше неопределенность пространства событий, тем больше информации содержит сообщение о его состоянии.
Немного усложним наше пространство событий. Пока все события, которые случались, были равновероятными. Но в реальных пространствах далеко не все события имеют равную вероятность. Скажем, вероятность того, что увиденная нами ворона будет черной, близка к 1. Вероятность того, что первый встреченный на улице прохожий окажется мужчиной, — примерно 0,5. Но встретить на улице Москвы крокодила почти невероятно. Интуитивно мы понимаем, что сообщение о встрече с крокодилом имеет гораздо большую информационную ценность, чем о черной вороне. Чем ниже вероятность события, тем больше информации в сообщении о таком событии.
Пусть пространство событий не такое экзотическое. Мы просто стоим у окна и смотрим на проезжающие машины. Мимо проезжают автомобили четырех цветов, о которых нам необходимо сообщить. Для этого мы закодируем цвета: черный — 00, белый — 01, красный — 10, синий — 11. Чтобы сообщить о том, какой именно автомобиль проехал, нам достаточно передать 2 бита информации.
Но довольно долго наблюдая за автомобилями, замечаем, что цвет автомобилей распределен неравномерно: черных — 50% (каждый второй), белых — 25% (каждый четвертый), красных и синих — по 12,5% (каждый восьмой). Тогда можно оптимизировать передаваемую информацию.
Больше всего черных автомобилей, поэтому обозначим черный — 0 — самый короткий код, а код всех остальных пусть начинается на 1. Из оставшихся половина белые — 10, а оставшиеся цвета начинаются на 11. В заключение обозначим красный — 110, а синий — 111.
Теперь, передавая информацию о цвете автомобилей, мы можем закодировать ее плотнее.
Энтропия по Шеннону
Пусть наше пространство событий состоит из n разных событий. При бросании монеты с двумя орлами такое событие ровно одно, при бросании одной правильной монеты — 2, при бросании двух монет или наблюдении за автомобилями — 4. Каждому событию соответствует вероятность его наступления. При бросании монеты с двумя орлами событие (выпадение орла) одно и его вероятность p1 = 1. При бросании правильной монеты событий два, они равновероятны и вероятность каждого — 0,5: p1 = 0,5, p2 = 0,5. При бросании двух правильных монет событий четыре, все они равновероятны и вероятность каждого — 0,25: p1 = 0,25, p2 = 0,25, p3 = 0,25, p4 = 0,25. При наблюдении за автомобилями событий четыре, и они имеют разные вероятности: черный — 0,5, белый — 0,25, красный — 0,125, синий — 0,125: p1 = 0,5, p2 = 0,25, p3 = 0,125, p4 = 0,125.
Это не случайное совпадение. Шеннон так подобрал энтропию (меру неопределенности в пространстве событий), чтобы выполнялись три условия:
Все эти требования вполне соответствуют нашим представлениям о неопределенности пространства событий. Если событие одно (первый пример) — никакой неопределенности нет. Если события независимы — неопределенность суммы равна сумме неопределенностей — они просто складываются (пример с бросанием двух монет). И, наконец, если все события равновероятны, то степень неопределенности системы максимальна. Как в случае с бросанием двух монет, все четыре события равновероятны и энтропия равна 2, она больше, чем в случае с автомобилями, когда событий тоже четыре, но они имеют разную вероятность — в этом случае энтропия 1,75.
Величина H играет центральную роль в теории информации в качестве меры количества информации, возможности выбора и неопределенности.
Клод Шеннон
Клод Элвуд Шеннон — американский инженер, криптоаналитик и математик. Считается «отцом информационного века». Основатель теории информации, нашедшей применение в современных высокотехнологических системах связи. Предоставил фундаментальные понятия, идеи и их математические формулировки, которые в настоящее время формируют основу для современных коммуникационных технологий.
В 1948 году предложил использовать слово «бит» для обозначения наименьшей единицы информации. Он также продемонстрировал, что введенная им энтропия эквивалентна мере неопределенности информации в передаваемом сообщении. Статьи Шеннона «Математическая теория связи» и «Теория связи в секретных системах» считаются основополагающими для теории информации и криптографии.
Во время Второй мировой войны Шеннон в Bell Laboratories занимался разработкой криптографических систем, позже это помогло ему открыть методы кодирования с коррекцией ошибок.
Шеннон внес ключевой вклад в теорию вероятностных схем, теорию игр, теорию автоматов и теорию систем управления — области наук, входящие в понятие «кибернетика».
Кодирование
И бросаемые монеты, и проезжающие автомобили не похожи на цифры 0 и 1. Чтобы сообщить о событиях, происходящих в пространствах, нужно придумать способ описать эти события. Это описание называется кодированием.
Кодировать сообщения можно бесконечным числом разных способов. Но Шеннон показал, что самый короткий код не может быть меньше в битах, чем энтропия.
Именно поэтому энтропия сообщения и есть мера информации в сообщении. Поскольку во всех рассмотренных случаях количество бит при кодировании равно энтропии, — значит кодирование прошло оптимально. Короче закодировать сообщения о событиях в наших пространствах уже нельзя.
При оптимальном кодировании нельзя потерять или исказить в сообщении ни одного передаваемого бита. Если хоть один бит потеряется, то исказится информация. А ведь все реальные каналы связи не дают 100-процентной уверенности, что все биты сообщения дойдут до получателя неискаженными.
Для устранения этой проблемы необходимо сделать код не оптимальным, а избыточным. Например, передавать вместе с сообщением его контрольную сумму — специальным образом вычисленное значение, получаемое при преобразовании кода сообщения, и которое можно проверить, пересчитав при получении сообщения. Если переданная контрольная сумма совпадет с вычисленной, вероятность того, что передача прошла без ошибок, будет довольно высока. А если контрольная сумма не совпадет, то необходимо запросить повторную передачу. Примерно так работает сегодня большинство каналов связи, например, при передаче пакетов информации по интернету.
Сообщения на естественном языке
Рассмотрим пространство событий, которое состоит из сообщений на естественном языке. Это частный случай, но один из самых важных. Событиями здесь будут передаваемые символы (буквы фиксированного алфавита). Эти символы встречаются в языке с разной вероятностью.
Самым частотным символом (то есть таким, который чаще всего встречается во всех текстах, написанных на русском языке) является пробел: из тысячи символов в среднем пробел встречается 175 раз. Вторым по частоте является символ «о» — 90, далее следуют другие гласные: «е» (или «ё» — мы их различать не будем) — 72, «а» — 62, «и» — 62, и только дальше встречается первый согласный «т» — 53. А самый редкий «ф» — этот символ встречается всего два раза на тысячу знаков.
Будем использовать 31-буквенный алфавит русского языка (в нем не отличаются «е» и «ё», а также «ъ» и «ь»). Если бы все буквы встречались в языке с одинаковой вероятностью, то энтропия на символ была бы Н = 5 бит, но если мы учтем реальные частоты символов, то энтропия окажется меньше: Н = 4,35 бит. (Это почти в два раза меньше, чем при традиционном кодировании, когда символ передается как байт — 8 бит).
Но энтропия символа в языке еще ниже. Вероятность появления следующего символа не полностью предопределена средней частотой символа во всех текстах. То, какой символ последует, зависит от символов уже переданных. Например, в современном русском языке после символа «ъ» не может следовать символ согласного звука. После двух подряд гласных «е» третий гласный «е» следует крайне редко, разве только в слове «длинношеее». То есть следующий символ в некоторой степени предопределен. Если мы учтем такую предопределенность следующего символа, неопределенность (то есть информация) следующего символа будет еще меньше, чем 4,35. По некоторым оценкам, следующий символ в русском языке предопределен структурой языка более чем на 50%, то есть при оптимальном кодировании всю информацию можно передать, вычеркнув половину букв из сообщения.
Другое дело, что не всякую букву можно безболезненно вычеркнуть. Высокочастотную «о» (и вообще гласные), например, вычеркнуть легко, а вот редкие «ф» или «э» — довольно проблематично.
Естественный язык, на котором мы общаемся друг с другом, высоко избыточен, а потому надежен, если мы что-то недослышали — нестрашно, информация все равно будет передана.
Но пока Шеннон не ввел меру информации, мы не могли понять и того, что язык избыточен, и до какой степени мы может сжимать сообщения (и почему текстовые файлы так хорошо сжимаются архиватором).
Избыточность естественного языка
В статье «О том, как мы ворпсиманием теcкт» (название звучит именно так!) был взят фрагмент романа Ивана Тургенева «Дворянское гнездо» и подвергнут некоторому преобразованию: из фрагмента было вычеркнуто 34% букв, но не случайных. Были оставлены первые и последние буквы в словах, вычеркивались только гласные, причем не все. Целью было не просто получить возможность восстановить всю информацию по преобразованному тексту, но и добиться того, чтобы человек, читающий этот текст, не испытывал особых трудностей из-за пропусков букв.
Почему сравнительно легко читать этот испорченный текст? В нем действительно содержится необходимая информация для восстановления целых слов. Носитель русского языка располагает определенным набором событий (слов и целых предложений), которые он использует при распознавании. Кроме того, в распоряжении носителя еще и стандартные языковые конструкции, которые помогают ему восстанавливать информацию. Например, «Она бла блее чвствтльна» — с высокой вероятностью можно прочесть как «Она была более чувствительна». Но взятая отдельно фраза «Она бла блее», скорее, будет восстановлена как «Она была белее». Поскольку мы в повседневном общении имеем дело с каналами, в которых есть шум и помехи, то довольно хорошо умеем восстанавливать информацию, но только ту, которую мы уже знаем заранее. Например, фраза «Чрты ее не бли лшны приятнсти, хтя нмнго рспхли и спллсь» хорошо читается за исключением последнего слова «спллсь» — «сплылись». Этого слова нет в современном лексиконе. При быстром чтении слово «спллсь» читается скорее как «слиплись», при медленном — просто ставит в тупик.
Оцифровка сигнала
Звук, или акустические колебания — это синусоида. Это видно, например, на экране звукового редактора. Чтобы точно передать звук, понадобится бесконечное количество значений — вся синусоида. Это возможно при аналоговом соединении. Он поет — вы слушаете, контакт не прерывается, пока длится песня.
При цифровой связи по каналу мы можем передать только конечное количество значений. Значит ли это, что звук нельзя передать точно? Оказывается, нет.
Разные звуки — это по-разному модулированная синусоида. Мы передаем только дискретные значения (частоты и амплитуды), а саму синусоиду передавать не надо — ее может породить принимающий прибор. Он порождает синусоиду, и на нее накладывается модуляция, созданная по значениям, переданным по каналу связи. Существуют точные принципы, какие именно дискретные значения надо передавать, чтобы звук на входе в канал связи совпадал со звуком на выходе, где эти значения накладываются на некоторую стандартную синусоиду (об этом как раз теорема Котельникова).
Теорема Котельникова (в англоязычной литературе — теорема Найквиста — Шеннона, теорема отсчетов) — фундаментальное утверждение в области цифровой обработки сигналов, связывающее непрерывные и дискретные сигналы и гласящее, что «любую функцию F(t), состоящую из частот от 0 до f1, можно непрерывно передавать с любой точностью при помощи чисел, следующих друг за другом через 1/(2*f1) секунд.
Помехоустойчивое кодирование. Коды Хэмминга
Если по ненадежному каналу передать закодированный текст Ивана Тургенева, пусть и с некоторым количеством ошибок, то получится вполне осмысленный текст. Но вот если нам нужно передать все с точностью до бита, задача окажется нерешенной: мы не знаем, какие биты ошибочны, потому что ошибка случайна. Даже контрольная сумма не всегда спасает.
Именно поэтому сегодня при передаче данных по сетям стремятся не столько к оптимальному кодированию, при котором в канал можно затолкать максимальное количество информации, сколько к такому кодированию (заведомо избыточному) при котором можно восстановить ошибки — так, примерно, как мы при чтении восстанавливали слова во фрагменте Ивана Тургенева.
Существуют специальные помехоустойчивые коды, которые позволяют восстанавливать информацию после сбоя. Один из них — код Хэмминга. Допустим, весь наш язык состоит из трех слов: 111000, 001110, 100011. Эти слова знают и источник сообщения, и приемник. И мы знаем, что в канале связи случаются ошибки, но при передаче одного слова искажается не более одного бита информации.
Предположим, мы сначала передаем слово 111000. В результате не более чем одной ошибки (ошибки мы выделили) оно может превратиться в одно из слов:
При передаче слова 001110 может получиться любое из слов:
Наконец, для 100011 у нас может получиться на приеме:
Заметим, что все три списка попарно не пересекаются. Иными словами, если на другом конце канала связи появляется любое слово из списка 1, получатель точно знает, что ему передавали именно слово 111000, а если появляется любое слово из списка 2 — слово 001110, а из списка 3 — слово 100011. В этом случае говорят, что наш код исправил одну ошибку.
Исправление произошло за счет двух факторов. Во-первых, получатель знает весь «словарь», то есть пространство событий получателя сообщения совпадает с пространством того, кто сообщение передал. Когда код передавался всего с одной ошибкой, выходило слово, которого в словаре не было.
Во-вторых, слова в словаре были подобраны особенным образом. Даже при возникновении ошибки получатель не мог перепутать одно слово с другим. Например, если словарь состоит из слов «дочка», «точка», «кочка», и при передаче получалось «вочка», то получатель, зная, что такого слова не бывает, исправить ошибку не смог бы — любое из трех слов может оказаться правильным. Если же в словарь входят «точка», «галка», «ветка» и нам известно, что допускается не больше одной ошибки, то «вочка» это заведомо «точка», а не «галка». В кодах, исправляющих ошибки, слова выбираются именно так, чтобы они были «узнаваемы» даже после ошибки. Разница лишь в том, что в кодовом «алфавите» всего две буквы — ноль и единица.
Избыточность такого кодирования очень велика, а количество слов, которые мы можем таким образом передать, сравнительно невелико. Нам ведь надо исключать из словаря любое слово, которое может при ошибке совпасть с целым списком, соответствующим передаваемым словам (например, в словаре не может быть слов «дочка» и «точка»). Но точная передача сообщения настолько важна, что на исследование помехоустойчивых кодов тратятся большие силы.
Сенсация
Понятия энтропии (или неопределенности и непредсказуемости) сообщения и избыточности (или предопределенности и предсказуемости) очень естественно соответствуют нашим интуитивным представлениям о мере информации. Чем более непредсказуемо сообщение (тем больше его энтропия, потому что меньше вероятность), — тем больше информации оно несет. Сенсация (например, встреча с крокодилом на Тверской) — редкое событие, его предсказуемость очень мала, и потому велика информационная стоимость. Часто информацией называют новости — сообщения о только что произошедших событиях, о которых мы еще ничего не знаем. Но если о случившемся нам расскажут второй и третий раз примерно теми же словами, избыточность сообщения будет велика, его непредсказуемость упадет до нуля, и мы просто не станем слушать, отмахиваясь от говорящего со словами «Знаю, знаю». Поэтому СМИ так стараются быть первыми. Вот это соответствие интуитивному чувству новизны, которое рождает действительно неожиданное известие, и сыграло главную роль в том, что статья Шеннона, совершенно не рассчитанная на массового читателя, стала сенсацией, которую подхватила пресса, которую приняли как универсальный ключ к познанию природы ученые самых разных специальностей — от лингвистов и литературоведов до биологов.
Но понятие информации по Шеннону — строгая математическая теория, и ее применение за пределами теории связи очень ненадежно. Зато в самой теории связи она играет центральную роль.
Семантическая информация
Шеннон, введя понятие энтропии как меры информации, получил возможность работать с информацией — в первую очередь, ее измерять и оценивать такие характеристики, как пропускная способность каналов или оптимальность кодирования. Но главным допущением, которое позволило Шеннону успешно оперировать с информацией, было предположение, что порождение информации — это случайный процесс, который можно успешно описать в терминах теории вероятности. Если процесс неслучайный, то есть он подчиняется закономерностям (к тому же не всегда ясным, как это происходит в естественном языке), то к нему рассуждения Шеннона неприменимы. Все, что говорит Шеннон, никак не связано с осмысленностью информации.
Пока мы говорим о символах (или буквах алфавита), мы вполне можем рассуждать в терминах случайных событий, но как только мы перейдем к словам языка, ситуация резко изменится. Речь — это процесс, особым образом организованный, и здесь структура сообщения не менее важна, чем символы, которыми она передается.
Еще недавно казалось, что мы ничего не можем сделать, чтобы хоть как-то приблизиться к измерению осмысленности текста, но в последние годы ситуация начала меняться. И связано это прежде всего с применением искусственных нейронных сетей к задачам машинного перевода, автоматического реферирования текстов, извлечению информации из текстов, генерированию отчетов на естественном языке. Во всех этих задачах происходит преобразование, кодирование и декодирование осмысленной информации, заключенной в естественном языке. И постепенно складывается представление об информационных потерях при таких преобразованиях, а значит — о мере осмысленной информации. Но на сегодняшний день той четкости и точности, которую имеет шенноновская теория информации, в этих трудных задачах еще нет.