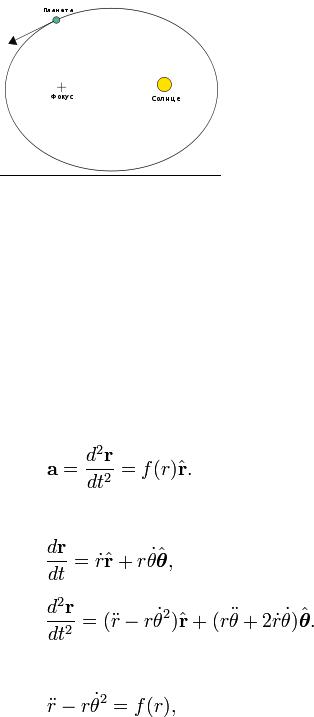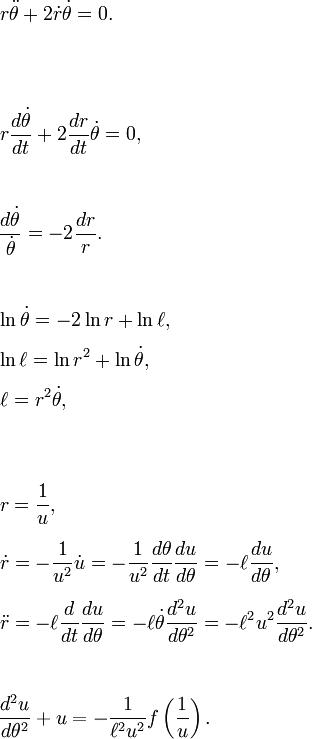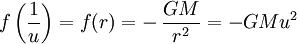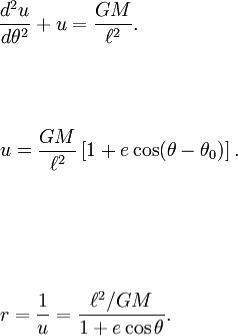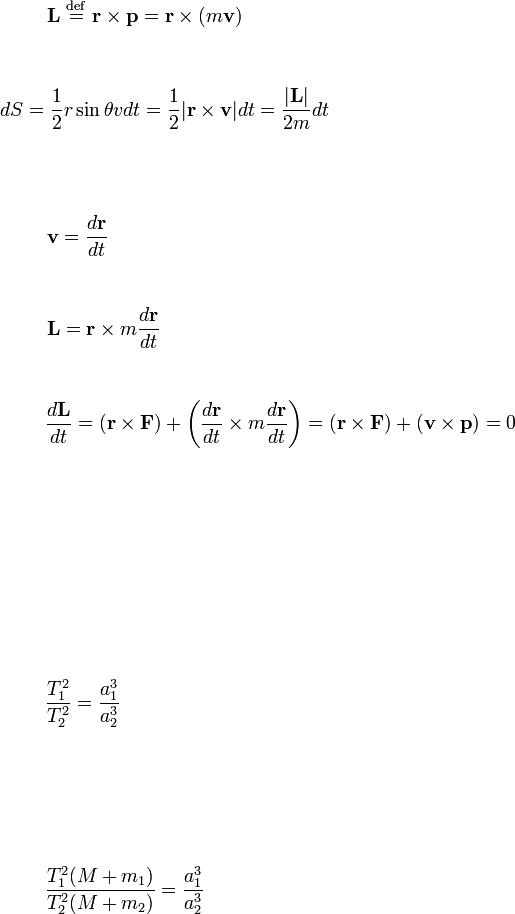фокальный параметр орбиты это

Журнал «Все о Космосе»

Орбита

Орбита (от лат. orbita — колея, дорога, путь) — траектория движения материальной точки в наперёд заданной системе пространственных координат для заданной в этих координатах конфигурации поля сил, которые на неё действуют. Термин был введён Иоганном Кеплером в книге «Новая астрономия» (1609).

В небесной механике это траектория небесного тела в гравитационном поле другого тела, обладающего значительно большей массой (планеты, кометы, астероида в поле звезды). В прямоугольной системе координат, начало которой совпадает с центром масс, траектория может иметь форму конического сечения (окружности, эллипса, параболы или гиперболы). При этом его фокус совпадает с центром масс системы.

Кеплеровы орбиты

Долгое время считалось, что планеты должны иметь круговую орбиту. После долгих и безуспешных попыток подобрать круговую орбиту для Марса, Кеплер отверг данное утверждение и, впоследствии, используя данные измерений, сделанных Тихо Браге, сформулировал три закона (Законы Кеплера), описывающих орбитальное движение тел.

Кеплеровыми элементами орбиты являются:

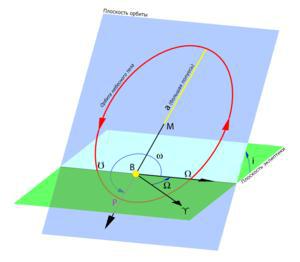
Эти элементы однозначно определяют орбиту независимо от её формы (эллиптической, параболической или гиперболической). Основной координатной плоскостью может быть плоскость эклиптики, плоскость галактики, плоскость земного экватора и т. д. Тогда элементы орбиты задаются относительно выбранной плоскости.

Классификация

По геометрической форме орбиты делятся на круговые и эллиптические, с тем или иным эксцентриситетом. Также существует разделение на замкнутые и незамкнутые орбиты, в особенности для КЛА.

По углу наклонения i плоскости орбиты к плоскости земного экватора — на экваториальные (i=0°), полярные (i=90°) и наклонные (i — любое, кроме 0° и 90°).

По соотношению периода обращения Т_об вокруг земного шара с земными или солнечными сутками — на не синхронные, квазисинхронные, синхронно-суточные (геосинхронные), солнечно-синхронные.

Источник

Орбита

Орби́та (от лат. orbita — колея, дорога, путь) — траектория движения материальной точки в наперёд заданной системе пространственных координат для заданной в этих координатах конфигурации поля сил, которые на неё действуют.

В небесной механике это траектория небесного тела в гравитационном поле другого тела, обладающего значительно большей массой (планеты, кометы, астероида в поле звезды). В прямоугольной системе координат, начало которой совпадает с центром масс, траектория может иметь форму конического сечения (окружности, эллипса, параболы или гиперболы). [1] При этом его фокус совпадает с центром масс системы.

Содержание

Кеплеровы орбиты

Долгое время считалось, что планеты должны иметь круговую орбиту. После долгих и безуспешных попыток подобрать круговую орбиту для Марса, Кеплер отверг данное утверждение и, впоследствии, используя данные измерений, сделанных Тихо Браге, сформулировал три закона (см. Законы Кеплера), описывающих орбитальное движение тел.

Эти элементы однозначно определяют орбиту независимо от её формы (эллиптической, параболической или гиперболической). Основной координатной плоскостью может быть плоскость эклиптики, плоскость галактики, плоскость земного экватора и т. д. Тогда элементы орбиты задаются относительно выбранной плоскости.

Классификация

По геометрической форме орбиты делятся на круговые и эллиптические, с тем или иным эксцентриситетом. Также существует разделение на замкнутые и незамкнутые орбиты, в особенности для КЛА.

По углу наклонения i плоскости орбиты к плоскости земного экватора — на экваториальные (i=0°), полярные (i=90°)и наклонные (i — любое, кроме 0° и 90°.

По соотношению периода обращения Т_об вокруг земного шара с земными или солнечными сутками — на не синхронные, квазисинхронные, синхронно-суточные (геосинхронные), солнечно-синхронные.

Источник

ГОС0Ы / 4 вопрос / Законы Кеплера и параметры орбиты

Законы Кеплера — три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел предельным переходом /→ 0, где, ,

— массы планеты и Солнца соответственно.

Первый закон Кеплера (закон эллипсов):

Доказательство первого закона Кеплера

Закон всемирного тяготения Ньютона гласит, что «каждый объект во Вселенной притягивает каждый другой объект по линии, соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a имеет форму.

Вспомним, что в полярных координатах:

В координатной форме запишем:

Подставляя и во второе уравнение, получим

После интегрирования запишем выражение

Уравнение движения в направлении становится равным

Закон всемирного тяготения Ньютона связывает силу на единицу массы с

расстоянием как

где G — универсальная гравитационная константа и M — масса звезды.

Это дифференциальное уравнение имеет общее решение:

для произвольных констант интегрирования e и θ0.

Заменяя u на 1/r и полагая θ0 = 0, получим:

Мы получили уравнение конического сечения с эксцентриситетом e и началом системы координат в одном из фокусов. Таким образом, первый закон Кеплера прямо следует из закона всемирного тяготения Ньютона и второго закона Ньютона.

Второй закон Кеплера (закон площадей):

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Доказательство второго закона Кеплера

Доказательство второго закона Кеплера

По определению угловой момент L точечной частицы с массой m и скоростью v записывается в виде:

где — радиус-вектор частицы а 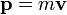импульс частицы. Площадь, заметаемая радиус-вектором r за время dt из геометрических соображений равна

В результате мы имеем

Продифференцируем обе части уравнения по времени^

пропорциональная ей скорость заметания площади — константа.

Третий закон Кеплера (гармонический закон)^

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

где T1 и T2 — периоды обращения двух планет вокруг Солнца, а a1 и a2 — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты/

где M — масса Солнца, а m1 и m2 — массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Параметры орбиты в плоскости:

В небесной механике это траектория небесного тела в гравитационном поле другого тела, обладающего значительно большей массой (планеты, кометы, астероида в поле звезды). В прямоугольной системе координат, начало которой совпадает с центром масс, траектория может иметь форму конического сечения (окружности, эллипса, параболы или гиперболы).[1] При этом его фокус совпадает с центром масс системы.

Долгое время считалось, что планеты должны иметь круговую орбиту. После долгих и безуспешных попыток подобрать круговую орбиту для Марса, Кеплер отверг данное утверждение и, впоследствии, используя данные измерений, сделанных Тихо Браге, сформулировал три закона (см. Законы Кеплера), описывающих орбитальное движение тел.

Кеплеровыми элементами орбиты являются:

эксцентриситет (е) — определяет форму орбиты,

наклонение орбиты (i),

долгота восходящего узла () — определяет положение плоскости орбиты небесного тела в пространстве,

аргумент перицентра ( ) — задаёт ориентацию аппарата в плоскости орбиты (часто задают направление на перицентр),

момент прохождения небесного тела через перицентр (To) — задаёт привязку по времени.

Эти элементы однозначно определяют орбиту независимо от её формы (эллиптической, параболической или гиперболической). Основной координатной плоскостью может быть плоскость эклиптики, плоскость галактики, плоскость земного экватора и т. д. Тогда элементы орбиты задаются относительно выбранной плоскости.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

ГОС0Ы / 4 вопрос / Законы Кеплера и параметры орбиты

Зако́ны Ке́плера — три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел предельным переходом /→ 0, где, , — массы планеты и Солнца соответственно.

Первый закон Кеплера (закон эллипсов):

Доказательство первого закона Кеплера

Закон всемирного тяготения Ньютона гласит, что «каждый объект во Вселенной притягивает каждый другой объект по линии, соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a имеет форму.

Вспомним, что в полярных координатах:

В координатной форме запишем:

Подставляя и во второе уравнение, получим

После интегрирования запишем выражение

Уравнение движения в направлении становится равным

Закон всемирного тяготения Ньютона связывает силу на единицу массы с расстоянием как

где G — универсальная гравитационная константа и M — масса звезды.

Это дифференциальное уравнение имеет общее решение:

для произвольных констант интегрирования e и θ0.

Заменяя u на 1/r и полагая θ0 = 0, получим:

Мы получили уравнение конического сечения с эксцентриситетом e и началом системы координат в одном из фокусов. Таким образом, первый закон Кеплера прямо следует из закона всемирного тяготения Ньютона и второго закона Ньютона.

Второй закон Кеплера (закон площадей):

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Доказательство второго закона Кеплера

Доказательство второго закона Кеплера

По определению угловой момент L точечной частицы с массой m и скоростью v записывается в виде:

где — радиус-вектор частицы а импульс частицы. Площадь, заметаемая радиус-вектором r за время dt из геометрических соображений равна

В результате мы имеем

Продифференцируем обе части уравнения по времени^

Третий закон Кеплера (гармонический закон)^

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

где T1 и T2 — периоды обращения двух планет вокруг Солнца, а a1 и a2 — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты/

где M — масса Солнца, а m1 и m2 — массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Параметры орбиты в плоскости:

В небесной механике это траектория небесного тела в гравитационном поле другого тела, обладающего значительно большей массой (планеты, кометы, астероида в поле звезды). В прямоугольной системе координат, начало которой совпадает с центром масс, траектория может иметь форму конического сечения (окружности, эллипса, параболы или гиперболы).[1] При этом его фокус совпадает с центром масс системы.

Долгое время считалось, что планеты должны иметь круговую орбиту. После долгих и безуспешных попыток подобрать круговую орбиту для Марса, Кеплер отверг данное утверждение и, впоследствии, используя данные измерений, сделанных Тихо Браге, сформулировал три закона (см. Законы Кеплера), описывающих орбитальное движение тел.

Кеплеровыми элементами орбиты являются:

эксцентриситет (е) — определяет форму орбиты,

наклонение орбиты (i),

долгота восходящего узла () — определяет положение плоскости орбиты небесного тела в пространстве,

аргумент перицентра () — задаёт ориентацию аппарата в плоскости орбиты (часто задают направление на перицентр),

момент прохождения небесного тела через перицентр (To) — задаёт привязку по времени.

Эти элементы однозначно определяют орбиту независимо от её формы (эллиптической, параболической или гиперболической). Основной координатной плоскостью может быть плоскость эклиптики, плоскость галактики, плоскость земного экватора и т. д. Тогда элементы орбиты задаются относительно выбранной плоскости.

Источник

Кеплеровы элементы орбиты

Кеплеровы элементы — шесть элементов орбиты, определяющих положение небесного тела в пространстве в задаче двух тел:

Первые два определяют форму орбиты, третий, четвёртый и пятый — ориентацию плоскости орбиты по отношению к базовой системе координат, шестой — положение тела на орбите.

Содержание

Большая полуось

Большая полуось — это половина главной оси эллипса (обозначена на рис.2 как ). В астрономии характеризует среднее расстояние небесного тела от фокуса

Эксцентриситет

Эксцентрисите́т (обозначается «» или «ε») — числовая характеристика конического сечения. Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия. [1] Эксцентриситет характеризует «сжатость» орбиты. Он выражается по формуле:

, где — малая полуось (см. рис.2)

Можно разделить внешний вид орбиты на пять групп:

Наклонение

Наклонение орбиты (накло́н орбиты, накло́нность орбиты, наклоне́ние) небесного тела — это угол между плоскостью его орбиты и плоскостью отсчёта (базовой плоскостью).

Обычно обозначается буквой i (от англ. inclination ). Наклонение измеряется в угловых градусах, минутах и секундах.

Зная наклонение двух орбит к одной плоскости отсчёта и долготы их восходящих узлов, можно вычислить угол между плоскостями этих двух орбит — их взаимное наклонение, по формуле косинуса угла.

Аргумент перицентра

Аргуме́нт перице́нтра — определяется как угол между направлениями из притягивающего центра на восходящий узел орбиты и на перицентр (ближайшую к притягивающему центру точку орбиты спутника), или угол между линией узлов и линией апсид. Отсчитывается из притягивающего центра в направлении движения спутника, обычно выбирается в пределах 0°-360°. Для определения восходящего и нисходящего узла выбирают некоторую (так называемую базовую) плоскость, содержащую притягивающий центр. В качестве базовой обычно используют плоскость эклиптики (движение планет, комет, астероидов вокруг Солнца), плоскость экватора планеты (движение спутников вокруг планеты) и т. д.

При исследовании экзопланет и двойных звёзд в качестве базовой используют картинную плоскость — плоскость, проходящую через звезду и перпендикулярную лучу наблюдения звезды с Земли. Орбита экзопланеты, в общем случае случайным образом ориентированная относительно наблюдателя, пересекает эту плоскость в двух точках. Точка, где планета пересекает картинную плоскость, приближаясь к наблюдателю, считается восходящим узлом орбиты, а точка, где планета пересекает картинную плоскость, удаляясь от наблюдателя, считается нисходящим узлом. В этом случае аргумент перицентра отсчитывается из притягивающего центра против часовой стрелки.

Обозначается ().

Долгота восходящего узла

Долгота́ восходя́щего узла́ — один из основных элементов орбиты, используемый для математического описания ориентации плоскости орбиты относительно базовой плоскости. Определяет угол в базовой плоскости, образуемый между базовым направлением на нулевую точку и направлением на точку восходящего узла орбиты, в которой орбита пересекает базовую плоскость в направлении с юга на север. Для тел, обращающихся вокруг Солнца, базовая плоскость — эклиптика, а нулевая точка — Первая точка Овна (точка весеннего равноденствия); угол измеряется от направления на нулевую точку против часовой стрелки.

Источник