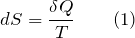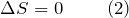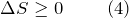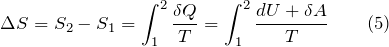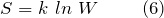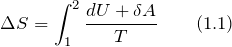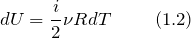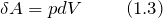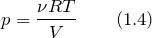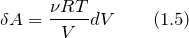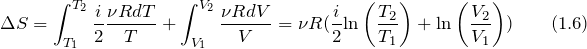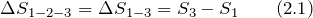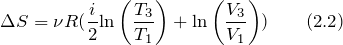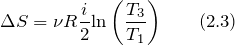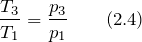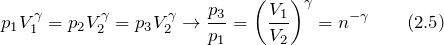функцией каких термодинамических параметров является энтропия

Энтропия в термодинамике

Вы будете перенаправлены на Автор24

Обычно любой физический процесс, при котором система постепенно переходит из одного состояния в другое, протекает по-разному, поэтому провести это явление в обратное состояние практически невозможно. Для этого необходимо использовать показатели промежуточного времени в окружающих определенную среду телах. Это напрямую связано с тем, что в процессе часть энергетического потенциала рассеивается путем постоянного трения и излучения.

Рисунок 1. Термодинамическая энтропия. Автор24 — интернет-биржа студенческих работ

Согласно законам термодинамики, практически все явления в природе необратимы. В любом физическом процессе часть энергии постепенно теряется. Для характеристики и описания рассеяния энергии вводится определение энтропии, объясняющее тепловое состояние концепции и определяющее вероятность возникновения нового состояния тела. Чем более вероятно это состояния, тем больше показатель энтропии. Все естественные ситуации в обычной жизни сопровождаются ростом данного элемента, который остается постоянным только в случае идеализированного процесса, наблюдаемого в замкнутой системе.

Энтропия – это универсальная функция состояния конкретной системы, незначительное изменение которой в обратимой ситуации равно отношению ничтожно малого количества введенной в данный процесс теплоты при соответствующей начальному состоянию температуре.

Поскольку энтропия есть основная функция состояния физического тела, то свойством интеграла выступает его самостоятельность и независимость от формы контура, по которому он вычисляется таким образом:

Готовые работы на аналогичную тему

Статистическое определение энтропии: принцип Больцмана

Рисунок 2. Статистический смысл энтропии. Автор24 — интернет-биржа студенческих работ

В 1877 году ученый Людвиг Больцман обнаружил, что энтропия концепции может относиться к числу вероятных «микросостояний», которые согласуются с основными термодинамическими свойствами. Хорошим примером такого явления выступает идеальный газ в сосуде. Микросостояние в указанном элементе определено как импульсы и позиции (моменты движения) каждого составляющего систему атома и молекула.

Комплексность предъявляет к ученым требования исследовать только те микросостояния, для которых:

Такой постулат, известный в науке как принцип Больцмана, возможно охарактеризовать в виде начала статистической механики, описывающего подробно главные термодинамические системы и использующего для своих целей принципы классической и квантовой физики.

Закон Больцмана связывает в термодинамике все микроскопические свойства системы с одним из её динамических свойств.

Согласно определению исследователя, энтропия является просто дополнительной функцией состояния, параметры которой могут быть только натуральным числом.

Понимание энтропии как меры беспорядка

Рисунок 3. Возрастание энтропии. Автор24 — интернет-биржа студенческих работ

Существует мнение, что энтропию возможно рассматривать, как меру беспорядка в определенной системе. Иногда, с научной точки зрения, это может быть оправдано, так как зачастую ученые в первую очередь думают об «упорядоченных» концепциях как элементах, имеющих практически нулевую возможность дальнейшего конфигурирования, а как о «нестабильных» системах, обладающих множеством вероятных состояний. Собственно, это просто переформулированное трактовка энтропии как количества микросостояний, действующих в определенной среде.

Подобное определение беспорядка и хаотичности термодинамической системы как основного параметра возможностей конфигурирования концепции практически дословно соответствует формулировке энтропии в виде микросостояний.

Проблемы начинаются в двух конкретных случаях:

В вышеуказанных случаях применение понятия энтропии в термодинамике абсолютно неправомерно.

Значение энтропии для живых организмов

Все трансформации и превращения внутренней энергии описываются в физике законами термодинамики, которые при адекватных физических моделях и грамотно сформулированных физических ограничениях вполне применимы и для жизненных нестабильных процессов. Уменьшение показателя энтропия (появление отрицательной энергии по Шрёдингеру) в живом организме при тесном взаимодействии его с окружающей средой автоматически приводит к росту свободного энергетического потенциала.

Если система «уклоняется» от постоянного равновесия, то она непременно должна в дальнейшем компенсировать увеличение энтропии другой энергией, с точки зрения науки — свободной энергией.

Таким образом, живая природа пытается избегать роста энтропии, повышая ее значимость в окружающей среде при общении с ней живого организма. Энтропия представляет собой «омертвленную» энергия, которую невозможно превратить в стабильную работу. По законам классической термодинамики в изолированных, хаотичных системах теплота полностью рассеивается, следовательно, процесс идет от порядка к хаосу.

Для живых микроорганизмов, как главных открытых систем, с научной точки зрения акт возникновения живого будет характеризоваться спонтанной трансформацией тепловой энергии необратимых функций в механическую целенаправленную работу создания высокоразвитой системы. Все это возможно осуществить посредством наличия свободной энергии. Следовательно, термодинамическая неравновесность существующих живых систем свидетельствует об их обязательной упорядоченности, так как полноценное равновесие соответствует хаосу и это в итоге приводит к смерти живого организма, когда его энтропия находится на максимальном уровне.

В целом, энтропия выступает как мера неопределенности и нестабильности, усреднения поведения физических объектов, установления правильного состояния и даже определенного единообразия. Жизнедеятельность биологических систем доказывает, что они не хотят подчиняться закону термодинамики для изолированной среды.

Источник

Энтропия в термодинамике

Понятие энтропии в термодинамике

Понятие энтропии ввел в XIX веке Р. Клаузиус. Энтропия (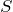) – это функция состояния, в обратимом процессе дифференциалом которой является величина :

где – количество теплоты, полученное термодинамической системой в ходе обратимого процесса; – термодинамическая температура системы.

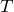
В любом обратимом круговом процессе изменение энтропии равно нулю:

Энтропия системы, которая совершает необратимый цикл, растет:

0\ \qquad (3)\]» title=»Rendered by QuickLaTeX.com»/>

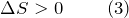
Выражения (2) и (3) относятся только к замкнутым системам, в том случае, если система обменивается теплотой с внешней средой, то энтропия может вести себя как угодно. Формулы (2) и (3) в единстве представляют собой неравенство Клаузиуса:

которое говорит о том, что в замкнутых системах при обратимых процессах, энтропия остается постоянной, а в необратимых процессах она растет.

В случае равновесного перехода из одного состояния в другое, в соответствии с определением энтропии (1), имеем:

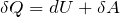
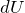
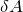
где по первому началу термодинамики. – изменение внутренней энергии термодинамической системы; – работа выполняемая системой. В формуле (5) подынтегральное выражение и пределы интегрирования следует выразить, используя параметры, которые характеризуют процесс, происходящий в термодинамической системе. Выражение (5) определяет энтропию с точностью до аддитивной постоянной. Физический смысл несет изменение энтропии, а не сама энтропия.

Свойство энтропии

Энтропия имеет свойство аддитивности: Энтропия совокупности тел равна сумме энтропий каждого тела, которое входит в систему.

Глубинный смысл энтропии открывает статистическая физика. Больцман установил, что энтропия системы связана с термодинамической вероятностью ():

где – постоянная Больцмана.

Напомним, что термодинамической вероятностью называют число способов, при помощи которых можно реализовать макросостояние термодинамической системы, или количество микросостояний, которые реализуют данное макросостояние.

В соответствии с (6) энтропия — это мера вероятности состояния термодинамической системы. Иногда, исходя из статистического толкования энтропии, говорят, что энтропия – мера неупорядоченности системы.

Примеры решения задач

Задание	Найдите изменение энтропии в процессах идеального газа.
Решение	В качестве основы для решения задачи используем формулу:

Для идеального газа изменение внутренней энергии:

Работа газа по определению равна:

Или, если учесть, что из уравнения Менделеева – Клайперона:

получаем, что элементарная работа идеального газа равна:

Подставим выражения (1.2) и (1.5) в определение изменения энтропии (1.1), получим:

Изменение энтропии при переходе из одного состояния в другое для идеального газа не зависит от процесса перехода.

Ответ

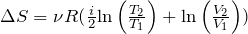
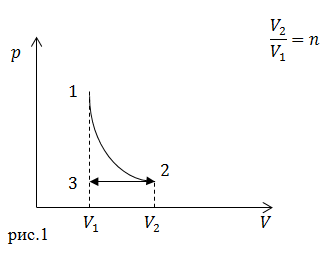
Задание

Идеальный газ ( 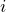– число степеней свободы молекулы газа) расширили по адиабате (процесс 1-2), причем 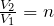, после этого изобарно сжали до первоначального объема (рис.1). Каково изменение энтропии газа в результате проведенных процессов?

РешениеТак как энтропия является функцией состояния, то ее изменение в процессах перехода от точки 1-2-3 можно заменить на изменение энтропии в переходе 1-3. То есть:

В качестве основы для решения задачи воспользуемся формулой, которую мы получили в примере 1:

Для изохорного процесса выражение (2.2) принимает вид:

Так как процесс 3-1 изохорный, то для него справедлив закон Шарля:

Воспользуемся уравнением адиабаты для процесса 1-2, и учтем, что процесс 2-3 изобарный, запишем:

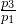
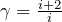
Подставим правую часть выражения (2.5) вместо отношения в формулу (2.3), примем во внимание, что имеем:

Источник

Энтропия (в термодинамике)

Термодинамические величины
Статья является частью серии «Термодинамика».
Энтропия
Количество теплоты
Термодинамическая работа
Химический потенциал
См. также: Термодинамические потенциалы.
Разделы термодинамики
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править

Термодинами́ческая энтропи́я S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы; её существование постулируется вторым началом термодинамики.

Содержание

Термодинамическое определение энтропии

Рудольф Клаузиус дал величине S имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

,

где — приращение (дифференциал) энтропии, а — бесконечно малое приращение количества теплоты.

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

Статистическое определение энтропии: принцип Больцмана

В 1877 году Людвиг Больцман нашёл, что энтропия системы может относиться к количеству возможных «микросостояний» (микроскопических состояний), согласующихся с их термодинамическими свойствами. Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых: (I) месторасположения всех частей расположены в рамках сосуда, (II) для получения общей энергии газа кинетические энергии атомов суммируются. Больцман постулировал, что:

где константу k=1,38•10 –23 Дж/К мы знаем теперь как постоянную Больцмана, а Ω является числом микросостояний, которые возможны в имеющемся макроскопическом состоянии (статистический вес состояния). Этот постулат, известный как принцип Больцмана, может быть оценен как начало статистической механики, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы (Ω) с одним из её термодинамических свойств (S).

Согласно определению Больцмана, энтропия является просто функцией состояния. Так как Ω может быть только натуральным числом (1,2,3,…), то энтропия Больцмана должна быть положительной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка

Существует мнение, что мы можем смотреть на Ω и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах, как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный «беспорядок», т.к. при этом будут максимальные возможности конфигурирования.

Границы применимости понимания энтропии как меры беспорядка

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

Рассмотрим оба пункта более подробно.

Однако многие учёные стали отождествлять информацию с «отрицательной энтропией» ввиду совпадения выражений для этих понятий. Начало этому заблуждению положил Н. Винер [3] (стр. 23). На самом деле энтропия не является мерой дезорганизации, мерой беспорядка и хаоса, а информация совсем не является мерой упорядоченности, организованности, порядка.

Рассмотрим второй случай неверного применения понятия энтропии.

Рассмотрим, например, набор 10 монет, каждая из которых может находиться либо в состоянии «орёл», либо в состоянии «решка». Наиболее «упорядоченным» макроскопическим состоянием будет являться или 10 «орлов», или 10 «решек»; для каждого результата в каждом случае имеется только одна возможная конфигурация. И наоборот, наиболее «неупорядоченное» состояние содержит 5 «орлов» и 5 «решек», и здесь 10 C₅ = 252 способов для получения этого результата (см. комбинаторика.)

Безусловно, этот пример также некорректен, т.к. система монет не является термодинамической системой, и поэтому термодинамическая энтропия системы в обоих случаях (как бы ни были перевёрнуты монеты) окажется, конечно, одинаковой. Т.о., разбросанные по комнате стулья не имеют отношения к термодинамической энтропии, хотя и могут иметь отношение к энтропии информационной.

Впрочем, это легко подтвердить на практике: замкнутая система 10 монет, перевёрнутых орлами вверх, самопроизвольно не перейдёт в систему хаотично перевёрнутых монет.

Энтропия в открытых системах

В силу второго начала термодинамики, энтропия замкнутой системы не может уменьшаться» (закон неубывания энтропии). Математически это можно записать так: , индекс обозначает так называемую внутреннюю энтропию, соответствующую замкнутой системе. В открытой системе возможны потоки тепла как из системы, так и внутрь неё. В случае наличия потока тепла в систему приходит количество тепла при температуре и уходит количество тепла при температуре . Приращение энтропии, связанное с данными тепловыми потоками, равно:

В стационарных системах обычно , T_<2>>» />, так что . Поскольку здесь изменение энтропии отрицательно, то часто употребляют выражение «приток негэнтропии», вместо оттока энтропии из системы. Негэнтропия определяется таким образом как обратная величина энтропии. Суммарное изменение энтропии открытой системы будет равно:

Если всё время 0>» />, то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если , то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру внешнего потока тепла в температуру уходящего из системы потока тепла.

Измерение энтропии

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объем V и давление P. Для измерения энтропии определенного состояния мы должны сперва измерить теплоёмкость при постоянных объёме и давлении (обозначенную C_V и C_P соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T согласно формуле:

где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

Таким образом, мы можем получить значение энтропии любого состояния (P,V) по отношению к первоначальному состоянию (P₀,V₀). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Построение графика изменения энтропии

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме P-V:

Здесь два замечания: (1) это не определение энтропии (но выведено из него), (2) предполагается, что C_V и C_P постоянные, что на самом деле не так.

См. также

Литература

Ссылки

Выделить Энтропия (в термодинамике) и найти в:

Источник