функционально графический метод решения задач с параметром
Графический метод решения задач с параметрами
Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.
Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.
Вот список тем, которые стоит повторить:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.
Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).
1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?
Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.
В первом уравнении выделим полный квадрат:
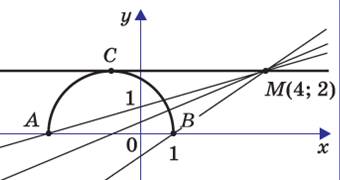
Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.
Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.
Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.
Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.
2. Найдите все значения a, при которых уравнение имеет единственное решение.
Уравнение равносильно системе:
Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).
Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.
Приводим подобные слагаемые в уравнении.
Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:
Решим систему графически:
Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением
Пусть С — точка касания.
Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.
Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.
Решая это уравнение, получаем, что
3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.
Второе уравнение при задает окружность с центром в точке и радиусом a.
Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.
, (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),
В — точка касания окружности и окружности
длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:
Есть еще точки С и D, в которых окружность касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:
, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.
Аналогично, для точки D:
и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.
4. При каких значениях a система уравнений имеет 4 решения?
И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!
Просто выделили полный квадрат во втором уравнении.
Сделаем замену Система примет вид:
Вот теперь все видно! Рисовать будем в координатах
Графиком первого уравнения является ромб, проходящий через точки с координатами и
Графиком второго уравнения является окружность с радиусом и центром в начале координат.
Когда же система имеет ровно 4 решения?
1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.
Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.
Диагонали нашего ромба равны 8 и 6. Значит, 
Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то
При этом Мы помним, что если окружность вписана в ромб, то диаметр этой окружности равен высоте ромба. Отсюда
2) Есть второй случай, и мы его найдем.
Пусть радиус окружности равен 3. Тогда система имеет 6 решений.
Значит, Объединим случаи и запишем ответ:
Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.
Графический метод в задачах с параметром
Данный метод используется не только в задачах с параметром, но и для решения обыкновенных уравнений, систем уравнений или неравенств. Он входит в стандартный курс школьной программы и наверняка вы с ним сталкивались, но в несколько упрощенном варианте. Сначала я кратко напомню, в чем заключается этот метод. Затем разберем, как его применять для решения задач с параметром, и рассмотрим несколько типовых примеров.
Для начала рассмотрим уравнение с одной переменной \(f(x)=0\). Для того, чтобы решить его графическим методом, нужно построить график функции \(y=f(x)\). Точки пересечения графика с осью абсцисс (ось \(х\)) и будут решениями нашего уравнения.
Или рассмотрим уравнение \(f(x)=g(x)\). Точно так же строим на одной координатной плоскости графики функций \(y=f(x)\) и \(y=g(x)\), абсциссы точек их пересечения будут решениями уравнения.
Стоит отдельно отметить, что для решения графическим методом необходимо выполнять очень качественный и точный рисунок.
Решить графическим методом уравнение \(x^2+3x=5x+3\).
Решение: Построим на одной координатной плоскости графики функций \(y=x^2+3x\) и \(y=5x+3\). См. рис.1.
\(y=5x+3\) – красный график; \(y=x^2+3x\) – синий график.
Из Рис.1 видно, что графики пересекаются в точках \((-1;2)\) и \((3;18)\). Таким образом, решением нашего уравнения будут: \(
Теперь рассмотрим уравнение с двумя переменными \(f(x,y)=0\). Решением этого уравнения будет множество пар точек \((x,y)\), которые можно изобразить в виде графика на координатной плоскости \((xOy)\). Если решать это уравнение аналитически, то, как правило, мы выражаем одну переменную через другую \((x,y=f(x))\) или \((x=f(y),y)\).
В качестве примера рассмотрим обыкновенное линейное уравнение \(2x-5y=10\). (1) Выражаем \(x=\frac<10+5y><2>\) – это называется общим решением уравнения. Изобразим его на координатной плоскости, построив график (Рис. 2):
О функционально-графическом методе решения задач с параметрами.
В задачах (уравнение, неравенство, система уравнений или неравенств) вида
(1)
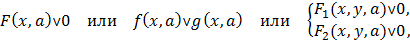
где символ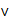 
заменяет один из знаков =, >,
3.2. Семейство функций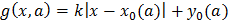 
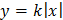
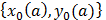
, графики которых получаются из графика 
параллельным переносом на вектор 
(семейство «уголков»).
3.3. Семейство окружностей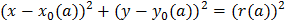 
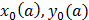
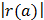
с центром в точке ( 
), радиуса 
.
При решении уравнения (неравенства) вида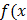 
) 
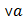
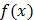
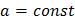
на плоскости Oxa строятся график функции 
(назовем его «неподвижным») и прямые 
, параллельные оси Ox. Далее в соответствии с условием задачи исследуется расположение построенных графиков.
Графический метод (геометрический).
Пример соответствия формул и графического образа.
Уравнение «пучка» прямых, проходящих через точку (4; 2):
.
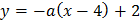
Плюсы и минусы графических методов в сравнении с аналитическими методами.
Применение графических методов оправдано в случаях, когда в условии задачи ставится вопрос о количестве решений в зависимости от значений параметра или о нахождении значений параметра, при которых решение отсутствует или единственно.
Плюсы графических методов:
· во-первых, построив графический образ, можно определить, как влияет на них и, соответственно, на решение изменение параметра;
· во-вторых, иногда график дает возможность сформулировать аналитически необходимые и достаточные условия для решения поставленной задачи;
· в-третьих, ряд теорем позволяет на основании графической информации делать вполне строгие и обоснованные заключения о количестве решений, об их границах и т.д.
Минусы графических методов: при использовании графических методов возникает вопрос о строгости решения. Требования к строгости должны определяться здравым смыслом. Если результат, полученный графическим методом, вызывает сомнения, его необходимо подкрепить аналитически.
Дата добавления: 2019-11-16 ; просмотров: 372 ; Мы поможем в написании вашей работы!
Функционально-графический подход к решению задач с параметрами
МУНИЦИПАЛЬНАЯ X УЧЕНИЧЕСКАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ « ЮНОСТЬ: ТВОРЧЕСТВО, ПОИСК, УСПЕХ»
Аннинский муниципальный район
Тема: « Функционально-графический подход к решению задач с параметрами »
Автор работы: Иванова Кристина
МБОУ Аннинская СОШ № 3, 9 «А» класс
Место выполнения работы: МБОУ Аннинская СОШ № 3, 9 «А» класс,
Воронежская область, п.г.т. Анна
г. АННА, 2020/2021 учебный год
3. Методические аспекты решения задачи № 22 2 части ОГЭ по математике (Модуль «Алгебра»)…………………………………………………………………………………..6 стр.
5. Способы задания функций…………………………………………………………. 8-10 стр.
6. Математическое понятие параметра……………………………………………..……11 стр.
7. Функционально-графический подход к решению задач с параметрами. 12-17 стр.
8. Проверь себя. 18 стр.
9. Полезные советы учащимся для успешной подготовки к ОГЭ по математике…. 19 стр.
11. Библиографический список…………………………………………………….……..22 стр.
12. 1. Элементарные функции в школьном курсе математики……………..….23-24 стр.
12. 2. Элементарные преобразования графиков функций……………………. 25-30 стр.
Изучение многих физических процессов и геометрических закономерностей часто приводит к решению уравнений, содержащих параметр. Решение задач с параметрами вызывает большие трудности у учащихся, так как их изучение не является отдельной составляющей школьного курса математики и рассматривается только на немногочисленных факультативных занятиях или учебных курсах.
Трудности при изучении данного вида уравнений связаны со следующими их особенностями: обилие формул и методов, используемых при решении уравнений данного вида; нехватка времени на них в школьной программе; исследовательский характер.
Объект исследования: задание №22 ОГЭ. Классы заданий, содержащих параметры, и их методы решения, а именно функционально-графический подход к решению заданий с параметрами.
Предмет исследования: графики функций.
Методы исследования: решение примеров на построения графиков, моделирование, сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, анализ и классификация информации.
Актуальность исследования обусловлена тем, что при подготовке к олимпиадам и успешной сдачи ОГЭ и ЕГЭ, выпускники испытывают затруднения при выполнении заданий, где при решении необходимо построить графики функций или при нахождении значении параметра. Не высок планируемый процент выполнения задания № 22- 3-15%.
Тема «Функции, их свойства и графики» является одной из важных тем курса алгебры основной школы. Она отражена в заданиях 1-й (базового уровня) и 2-й (повышенного и высокого уровня) частях экзаменационной работы.
Цель исследования: расширение математических представлений о приемах и методах решения задач с параметрами и углубление знаний по построению графиков функций; оказание практической помощи выпускникам 9 класса в приобретении, освоении и закреплении знаний как теоретического, так и практического характера по теме «Функция» на ОГЭ и ГВЭ, а так же с целью повышения уровня самоподготовки к ОГЭ по математике.
Проблема, предмет, гипотеза исследования обусловили следующие задачи :
Подобрать необходимую литературу, проанализировать и систематизировать полученную информацию.
2. Рассмотреть графический способ решения уравнений и систем уравнений с параметрами.
3. Показать применение данных способов при решении заданий ОГЭ № 22.
Практическая значимость моей работы заключается:
1. В использовании приобретенных знаний по данной теме, а также углубление их и применение к другим функциям и уравнениям;
2. В использовании навыков исследовательской работы в дальнейшей учебной деятельности.
Ключевые слова : график, параметр, ОГЭ, алгебра.
2. Историческая справка.
В первой половине ХVII века начинает складываться представление о функции как о зависимости одной переменной величины от другой. Так, французские математики Пьер Ферма (1601-1665) и Рене Декарт (1596-1650) представляли себе функцию как зависимость ординаты точки кривой от её абсциссы. А английский ученый Исаак Ньютон (1643-1727) понимал функцию как изменяющуюся в зависимости от времени координату движущейся точки.
Термин «функция» (от латинского function – исполнение, совершение) впервые ввел немецкий математик Готфрид Лейбниц (1646-1716). У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем швейцарский математик Иоганн Бернулли (1667-1748) и член Петербургской Академии наук знаменитый математик XVIII века Леонард Эйлер (1707-1783) рассматривали функцию как аналитическое выражение. У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.1
К концу XIX века понятие функции переросло рамки числовых систем. Сначала понятие функции было распространено на векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.2
3. Методические аспекты решения задачи № 22 2 части ОГЭ по математике
Задания второй части модуля «Алгебра» направлены на проверку владения таких качеств математической подготовки выпускников, как:
формально-оперативным алгебраическим аппаратом;
умения решить комплексную задачу, включающую в себя знания из разных тем курса алгебры;
умения математически грамотно и ясно записать решение, приводя при этом необходимые пояснения и обоснования;
владения широким спектром приёмов и способов рассуждений.
Основные проверяемые требования к математической подготовке при выполнении задания 22.
Основные проверяемые требования к математической подготовке
Разделы элементов содержания
Разделы элементов требований
Максимальный балл за выполнение задания
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели.
2. Алгебраические выражения. 3.Уравнения и неравенства. 4.Числовые последовательности.
5. Функции и графики.
6. Координаты на прямой и плоскости.
4. Уметь строить и читать графики функций. 2. Уметь выполнять преобразования алгебраических выражений.
Задания второй части считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается балл, на 1 меньше указанного.
Основным условием получения положительной оценки за решение задания 22 является верное построение графика. А верное построение графика включает в себя следующее: правильно подобранный и отображенный на рисунке масштаб, содержательную таблицу значений или объяснение построения, выколотую точку (точки), обозначенную в соответствии с ее координатами.
В данных задачах требуется построить график и затем найти значение параметра,
то есть для каждого допустимого значения параметра найти множество всех решений данного уравнения (неравенства, системы) или доказать, что их нет.
Очень часто встречаю задания, где на различных участках числовой прямой функция задана разными формулами. Такие функции назовём кусочными. Участки числовой прямой, которые различаются формулами задания, назовём составляющими область определения, а их объединение, является областью определения кусочной функции. Точки, которые делят область определения на составляющие, называются граничными точками. Выражения, определяющие кусочную функцию на каждой составляющей области определения, называется входящими функциями.
Наличие таких свойств как чётность, нечётность, нули функции, промежутки знакопостоянства, монотонность, ограниченность у кусочных функций устанавливается согласно общепринятым определениям, с учётом особенностей составляющих области определения и входящих функций.
Для того чтобы вычислить значение кусочной функции в заданной точке, необходимо, во-первых, определить, какой составляющей области определения принадлежит эта точка, а, во-вторых, найти значение входящей функции на этой составляющей.
Чтобы построить график кусочной функции, нужно:
Построить в одной системе координат графики входящих функций,
Выяснить значение функции в граничных точках.
Если каждая входящая кусочной функции является линейной, то будем называть её кусочно-линейной функцией.
5. Способы задания функций.
Функция – одно из важнейших математических понятий. Функцией называют такую зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение переменной у.
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.
1. Аналитический способ (функция задается с помощью математической формулы).
2. Табличный способ (функция задается с помощью таблицы)
3. Описательный способ (функция задается словесным описанием)
4. Графический способ (функция задается с помощью графика)
Табличный способ довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является конечным множеством.
При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.
Функция может быть определена разными формулами на разных участках области своего задания.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Словесный способ. Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле. «Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».3
Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически.
Способы задания линейной функции.
Прямая линия, пересекающая оси координат в точках (0;3) и (-1,5;0)
6. Математическое понятие параметра.
Параметр – величина, характеризующая какое-нибудь основное свойство устройства, системы. («Словарь русского языка» С.И. Ожегова.)
Параметр – постоянная величина, выраженная буквой, сохраняющая свое постоянное значение лишь в условиях данной задачи. («Словарь иностранных слов».)
Параметр – это величина, входящая в математическую формулу и сохраняющая постоянное значение в пределах одного явления или для данной частной задачи, но при переходе к другому явлению или другой задаче меняющая свое значение. («Толковый словарь русского языка» под редакцией Д.Н. Ушакова.)
П 
ример:
Нельзя научиться решать любые задачи с параметрами, используя какой-то алгоритм или формулы. При решении задач с параметрами надо всегда активно использовать соображения, исходящие из здравого смысла, рассматривать их как задачи исследовательские.
7. Функционально-графический подход к решению задач с параметрами.
Согласно открытому банку задач ОГЭ, задание № 22 представляет собой задание с параметром. Задание выглядит примерно так: « Постройте график функции 
и определите, при каких значениях параметра прямая y = m имеет с графиком _ общие точки».
Чтобы выполнить данное задание надо владеть графическим способом решения. Нужно хорошо представляет себе движение графиков относительно осей при изменении параметра. Суть метода в том, чтобы нарисовать график функции при фиксированном значении параметра, а потом посмотреть, как будет двигаться график при изменении параметра. Для этого лучше иметь бумагу в клетку и уметь рисовать графики функций, что порой непросто.
Задачи, содержащие параметр, требуют к себе своеобразный подход, здесь необходимо грамотное и тщательное исследование. Для применения графических методов требуется умение выполнять дополнительное построение различных графиков, вести графические исследования, соответствующие данным значениям параметра.
Уравнения с параметром вызывают серьезные трудности логического характера. Каждое такое уравнение – это, по существу, краткая запись семейства уравнений. Ясно, что выписать каждое уравнение из бесконечного семейства невозможно, но, тем не менее, каждое из них должно быть решено. Легче всего это сделать с помощью графического представления зависимости переменной 
от параметра 
.
На плоскости 
функция 
задает семейство кривых, зависящих от параметра а.
У 
простим выражение:
Ответ: 
Р 
Построим график функции
Раскрывая модули, получаем
Следовательно, уравнение f ( x )= a имеет хотя бы одно решение, если a ≥ 0,5
Правая часть данного уравнения может быть только неотрицательной, т.е. k 0
4 
. Постройте график функции у = и определите, при каких значениях параметра a прямая y = a имеет с графиком три корня.
б 
) графиком функции у = а является прямая, параллельная оси ОХ, проходящая через точку (0;а).
При а = 4 прямая с графиком имеют три общие точки.
55. Постройте график функции 
и определите, при каких значениях параметра c прямая y = c имеет с графиком ровно одну общую точку.
Разложим числитель дроби на множители:
При x ≠3 и x ≠-2 функция принимает вид:
Её график — парабола c выколотыми точками
Прямая y = c имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая.
Вершина параболы имеет координаты (-0,5;-6,25).
76. Постройте график функции у = 
и определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку.
= ( x +4)( x +2) = x 2 + 6 x + 8
График функции сводится к графику параболы у = x 2 + 6 x + 8 с выколотой точкой (-1; 3)
8. Постройте график функции 
и определите, при каких значениях параметра a прямая y = a имеет с графиком одну общую точку.
З 
апишем уравнение в виде:
Построим графики функций:
и подвижную прямую у = а.
9. Постройте график функции 
и определите, при каких значениях параметра a прямая y = a не имеет с графиком общих точек.
Построим график и прямую у = а.
По рисунку видим при а
Ответ: 
8 
. Проверь себя!
9. Полезные советы учащимся для успешной подготовки к ОГЭ по математике.
1. Не секрет, что успешнее сдает экзамен тот, кто в полном объеме владеет материалом, хорошо знаком с процедурой проведения экзамена, психологически готов к экзамену и адекватно реагирует на нестандартные ситуации.
2. Хорошо знать документы, регламентирующие проведение экзамена по математике:
«Кодификатор требований к уровню подготовки обучающихся для проведения основного государственного экзамена по математике»
«Кодификатор элементов содержания для проведения основного государственного экзамена по математике»;
«Спецификация контрольных измерительных материалов для проведения основного государственного экзамена по математике»;
«Демонстрационный вариант контрольных измерительных материалов для проведения основного государственного экзамена по математике»;
Литературу для подготовки к ОГЭ.
Список сайтов, содержащих демоверсии и позволяющие онлайн-тестироваться.
3. На основании школьного плана подготовки к экзамену, составить личный план, включив в него консультации, которые проводит учитель, расписание «пробных» ОГЭ.
4. Тщательно анализировать пробные ОГЭ. По итогам пробных ОГЭ корректировать самостоятельную подготовку к экзамену.
5. Собирать свой портфолио-папку со всеми выполненными пробниками. Вести мониторинг выполнения всех заданий пробных экзаменов.
6. Серьезное внимание уделять устному счету, который проводит учитель на уроках. Эти упражнения активизируют мыслительную деятельность, требуют осознанного усвоения учебного материала. При их выполнении развивается память, речь, внимание, быстрота реакции. Устные упражнения позволяют корректировать знания, умения и навыки учащихся, а также автоматизировать навыки простейших вычислений и преобразований.
7. Научиться «читать» условие задачи до начала решения и после ее решения для того, чтобы верно ответить на поставленный вопрос (что нужно было найти?).
Математика – это набор инструментов, который необходим в познании окружающего мира. И этим инструментом необходимо владеть в совершенстве, чтобы познавать, развивать и изменять нашу жизнь.
Все изученные в школе функции относятся к классу элементарных функций, и строить графики этих функций интересно и просто. А график является портретом функции, поэтому выполнять задания следует после того, как изучен весь теоретический материал по теме.
В своей работе я обобщила знания о функции, о их графиках и свойствах. Изучила и систематизировала прототипы заданий № 23 ОГЭ, привела алгоритмы их решения. В процессе этой работы наглядно видно, что задания по теме «Функции», представленные в разных вариантах, имеют не одинаковый уровень сложности.
Данные задачи представляют большой интерес для учащихся девятых классов, так как они встречаются в КИМах ОГЭ. Умение строить данные графики функций позволит более успешно сдать экзамен.
Считаю, что готовясь к итоговому экзамену учащимся необходимо ориентироваться на задания более высокой сложности и тогда можно рассчитывать на положительный результат. Учащиеся выпускного класса должны иметь более высокий уровень теоретических знаний и умений правильно применять их.
Надеюсь, что данная работа поможет не только экзаменуемым, но и учителям, при подготовке к ОГЭ.
В моем понимании жизнь – это функция, зависящая от многих переменных.
Мы получаем от жизни то, во что верим. Ты веришь, что жизнь прекрасна — и она прекрасна. Ты веришь, что она ужасна, — она ужасна. Веришь, что выхода нет, — и не найдешь выхода. Веришь, что выход есть, — обязательно его увидишь. Ты веришь в успех — ты его создашь. Наша вера создает нашу реальность. Если полагаться исключительно на судьбу и шагать по случайным цепочкам событий, созданных косвенно другими людьми, «плыть по течению», можно выплыть не на тот берег. Разумеется, жизнь вносит коррективы в наши планы, и порой возникают различные обстоятельства, но я думаю, что все в наших руках.
«Математические сведения могут применяться умело и с пользой только в том случае, если они усвоены творчески, так, что учащийся видит сам, как можно было бы прийти к ним самостоятельно». А.Н. Колмогоров.
12. 1 Элементарные функции в школьном курсе математики.