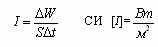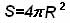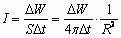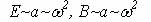гипотеза максвелла о вихревом электрическом поле
Почему теорию Максвелла так трудно понять?
Скромность не всегда добродетель
В 1865 году Джеймс Клерк Максвелл опубликовал свою статью “Динамическая теория электромагнитного поля» в «Философских трудах Королевского общества». Ему было тогда тридцать четыре года. Оглядываясь назад, мы можем заметить, что работа Максвелла была самым важным событием девятнадцатого века в истории физических наук. Если говорить в общем о естественных науках, то статья Максвелла была второй по значимости после «Происхождения видов» Дарвина. Но важность работ Максвелла не была очевидна для его современников. Более двадцати лет его теория электромагнетизма в основном игнорировалась. Физикам было трудно ее понять из-за обилия сложных уравнений. Математикам было трудно ее понять, потому что Максвелл использовал для объяснений физический язык. Этот труд был расценен как неясное предположение без должного количества экспериментальных доказательств. Физик Михаил Пупин в своей автобиографии «От иммигранта к изобретателю» описывает, как он путешествовал из Америки в Европу в 1883 году в поисках того, кто понимал Максвелла. Он отправился изучать теорию Максвелла, как рыцарь в поисках Святого Грааля.
Пупин сначала поступил в Кембридж с твердым намерением изучить теорию у самого Максвелла. Он не знал, что Максвелл умер четыре года назад. Узнав, что Максвелл умер, он остался в Кембридже и был назначен преподавателем колледжа. Но его наставник знал о теории Максвелла меньше, чем он сам, и был заинтересован только в том, чтобы научить Михаила решать математические задачи трипоса. Михаил Пупин был поражен, обнаружив, как он говорит, «как мало было физиков, которые уловили смысл теории, даже через двадцать лет после того, как она была сформулирована Максвеллом в 1865 году». В конце концов он бежал из Кембриджа в Берлин и поступил студентом к Герману фон Гельмгольцу. Гельмгольц понимал теорию и учил Пупина тому, что знал сам. Пупин вернулся в Нью-Йорк, стал профессором Колумбийского университета и обучал последующие поколения студентов, которые впоследствии распространили Евангелие Максвелла по всей Америке.

Как случилось, что теория Максвелла была так широко проигнорирована? В конце концов, Максвелл не был похож на своего современника Грегора Менделя, монаха, работавшего в безвестном монастырском саду в Богемии. Максвелл был известным профессором, директором Кавендишской лаборатории в Кембридже, ведущей фигурой в британском научном сообществе. Свидетельством его высокого положения можно считать то, что он был президентом секции А (математические и физические науки) Британской ассоциации содействия развитию науки, когда ассоциация провела свое ежегодное собрание в Ливерпуле в 1870 году. Он выступил с президентской речью в Ливерпуле, которая была опубликована во втором томе недавно основанного журнала «Nature». Стиль его выступления показывает нам, почему его теорию не воспринимали всерьез. Можно было ожидать, что он воспользуется возможностью, предоставленной президентской платформой, чтобы объявить миру о важности открытий, которые он сделал пять лет назад. Он не сделал ничего подобного. Он был абсурдно и раздражающе скромен.
Теория, которую сэр Уильям основал на великолепных гидродинамических теоремах Гельмгольца, ищет свойства молекул в кольцевых вихрях однородной несжимаемой жидкости без трения. Гельмгольц показал, что в идеальной жидкости такое кружащееся кольцо, если оно однажды возникло, будет продолжать кружиться вечно, всегда будет состоять из той же самой части жидкости, которая была сначала закручена, и никогда не может быть разрезана надвое какой-либо естественной причиной. Эти кольцевые вихри способны к таким разнообразным связям и узловатым самоинволюциям, что свойства различных узловатых вихрей должны быть столь же различны, как и свойства различных видов молекул.
И так далее. Максвелл объяснил, как древняя теория о том, что материя состоит из атомов, столкнулась с логическим парадоксом. С одной стороны, атомы должны были быть твердыми, непроницаемыми и неразрушимыми. С другой стороны, данные спектроскопии и химии показали, что атомы имеют внутреннюю структуру и находятся под влиянием внешних сил. Этот парадокс в течение многих лет блокировал прогресс в понимании природы материи. Теперь, наконец, вихревая теория молекул разрешила парадокс. Вихри в эфире мягкие и имеют внутреннюю структуру, и тем не менее, согласно Гельмгольцу, они индивидуальны и неразрушимы. Оставалось только вывести факты спектроскопии и химии из законов взаимодействия вихрей, предсказанных гидродинамикой идеальной жидкости. Максвелл считал эту вихревую теорию материи замечательным примером плодотворного взаимодействия математики и физики.
Неясно, верил ли Максвелл всерьез в то, что говорил о вихревой теории. Возможно, он хотел, чтобы его речь развлекала слушателей, а не просвещала их. У него было хитрое чувство юмора, и вполне возможно, что он хвалил теорию вихря, зная, что более проницательные члены аудитории поймут, что теория была шуткой. Только в конце своего выступления Максвелл кратко упомянул о своей теории электромагнетизма.
Другая теория электричества, которую я предпочитаю, отрицает действие на расстоянии и приписывает электрическое действие напряжениям и давлениям во всепроникающей среде, причем эти напряжения одинаковы по характеру с теми, которые известны инженерам, и среда идентична той, в которой предполагается распространение света.
Фраза «Другая теория электричества, которую я предпочитаю», кажется, намеренно скрывает тот факт, что это была его собственная теория. Неудивительно, что вихри Кельвина произвели на его слушателей большее впечатление, чем уравнения Максвелла.
Мораль этой истории заключается в том, что скромность не всегда является добродетелью. Максвелл и Мендель оба были чрезмерно скромны. Скромность Менделя задержала прогресс биологии на пятьдесят лет. Скромность Максвелла замедлила прогресс физики на двадцать лет. Для прогресса науки будет лучше, если люди, делающие великие открытия, не будут слишком скромны, чтобы трубить в свои собственные трубы. Если бы у Максвелла было такое же эго, как у Галилея или Ньютона, он бы позаботился о том, чтобы его работы не игнорировались. Максвелл был таким же великим ученым, как Ньютон, и гораздо более приятным человеком. Но, к сожалению, он не начал президентскую речь в Ливерпуле словами, подобными тем, которые Ньютон использовал, чтобы представить третий том своей Principia Mathematica: «. исходя из тех же принципов, я теперь демонстрирую структуру системы мира». Ньютон не называл свой закон всемирного тяготения «очередной теорией тяготения, которую я предпочитаю».
Теория Максвелла и квантовая механика
Помимо скромности Максвелла, были и другие причины, по которым его теорию было трудно понять. Он заменил ньютоновскую вселенную материальных объектов, взаимодействующих друг с другом на расстоянии, вселенной полей, простирающихся через пространство и взаимодействующих только локально с материальными объектами. Понятие поля было трудно понять, потому что поля неосязаемы. Ученые того времени, включая самого Максвелла, пытались представить поля как механические структуры, состоящие из множества маленьких колесиков и вихрей, простирающихся в пространстве. Эти структуры должны были переносить механические напряжения, которые электрические и магнитные поля передавали между электрическими зарядами и токами. Чтобы поля удовлетворяли уравнениям Максвелла, система колес и вихрей должна была быть чрезвычайно сложной.

Через шестьдесят лет после того, как Максвелл опубликовал свою теорию, Шредингер, Гейзенберг и Дирак изобрели квантовую механику. Квантовая механика была принята гораздо быстрее, чем теория Максвелла, потому что она сделала множество определенных предсказаний об атомных процессах и эксперименты показали, что все предсказания были правильными. Через год-два все поверили в квантовую механику как в практический инструмент для расчета основных процессов физики и химии. Природа, очевидно, подчинялась законам квантовой механики. Но значение квантовой механики оставалось спорным. Хотя квантовая механика была быстро принята, она не была быстро понята. Резкие расхождения во мнениях по поводу интерпретации квантовой механики сохраняются на протяжении семидесяти лет.

Для понимания квантовой механики может оказаться полезным подчеркнуть сходство между квантовой механикой и теорией Максвелла. В двух отношениях теория Максвелла может дать ключ к тайнам квантовой механики.
Вторая связь между теорией Максвелла и квантовой механикой заключается в глубоком сходстве структуры. Подобно теории Максвелла, квантовая механика делит Вселенную на два слоя. Первый слой содержит волновые функции Шредингера, матрицы Гейзенберга и векторы состояний Дирака. Величины в первом слое подчиняются простым линейным уравнениям. Их поведение можно точно рассчитать. Но их нельзя наблюдать непосредственно. Второй слой содержит вероятности столкновений и превращений частиц, интенсивности и поляризации излучения, математические ожидания энергий и спинов частиц. Величины во втором слое могут быть непосредственно наблюдаемы, но не могут быть непосредственно вычислены. Они не подчиняются простым уравнениям. Это либо квадраты величин первого слоя, либо произведения одной величины первого слоя на другую. В квантовой механике, как и в теории Максвелла, Природа живет в абстрактном математическом мире первого слоя, но мы, люди, живем в конкретном механическом мире второго слоя. Мы можем описать Природу только абстрактным математическим языком, потому что наш вербальный язык находится дома только во втором слое.
Все эти теории основаны на концепции динамических полей, введенной Максвеллом в 1865 году. Все они имеют одинаковую двухслойную структуру, отделяющую мир простых динамических уравнений от мира человеческого наблюдения. Все они воплощают в себе то же качество математической абстракции, которое сделало теорию Максвелла трудной для понимания его современниками. Мы можем надеяться, что глубокое понимание теории Максвелла приведет к рассеиванию тумана непонимания, который все еще окружает интерпретацию квантовой механики. И мы можем надеяться, что глубокое понимание теории Максвелла поможет проложить путь к дальнейшим триумфам физики в XXI веке.
Гипотеза Максвелла
Генератор высокочастотных колебаний возбуждает в вибраторе вынужденные электромагнитные колебания, что приводит к ускоренному движению электронов и появлению переменного тока. Вокруг вибратора возникает переменное магнитное поле.
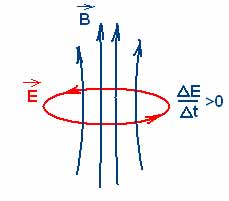
Используя новую трактовку закона электромагнитной индукции, открытого М.Фарадеем в 1831 г., Дж.Максвелл ввел в физику понятие вихревого электрического поля: Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты.
Максвелл высказал гипотезу о существовании и обратного процесса:
Изменяющееся во времени электрическое поле порождает в окружающем пространстве магнитное поле.
Гипотеза Максвелла была лишь теоретическим предположением, не имеющим экспериментального подтверждения, однако на ее основе Максвеллу удалось записать непротиворечивую систему уравнений, описывающих взаимные превращения электрического и магнитного полей, т. е. систему уравнений электромагнитного поля (уравнений Максвелла).
Из теории Максвелла вытекает ряд важных выводов :
Электромагнитные волны поперечны – векторы Е и В перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны.
2. Электромагнитные волны распространяются в веществе с конечной скоростью
Скорость c=300000 км/с распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.
3. В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные “партнеры” единого электромагнитного поля.
Таким образом, электромагнитная волна в приемном диполе возбуждает вынужденные электромагнитные колебания, что приводит к возникновению переменного тока и свечению лампочки.
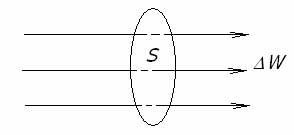
Электромагнитные волны, распространяясь в пространстве, несут с собой энергию:
W=Wэ+Wм
Плотность потока электромагнитного излучения (интенсивность волны) через поверхность площадью S будет равна:
При наличии точечного источника излучения интенсивность распространяющейся электромагнитной волны по всем направлениям одинакова. Если площадь поверхности сферы:
Известно, что напряженность электрического поля и магнитная индукция пропорциональны квадрату частоты:
Полная плотность потока электромагнитного излучения:
Гипотеза максвелла о вихревом электрическом поле
«Мое право говорить ваше право не слушать»
Развитие Вихревого Поля Максвелла
» В 1865 г. Максвелл высказал гипотезу о том, что изменение электрического поля в окружающем пространстве должно вызывать образование магнитного поля. В дальнейшем эта гипотеза нашла экспериментальное подтверждение.
Переменное электрическое поле, которое может создавать переменное магнитное поле, Максвелл назвал током смещения. » (Википедиа)
Мое развитие Вихревого поля Максвелла в этой статье состоит в том, что я показываю во-первых, более детально как в пространстве теоретически и практически образуются вихревые поля, какие виды этого поля существуют, что является причиной их образования, и, во-вторых, что природное существование вихревых полей является источником свободной электрической энергии и т. далее.
Переменное электрическое поле в плоском конденсаторе
Рис. А
Как получить вихревое поле
Наглядным примером в этом отношении является существование переменного электрического поля в пространстве между обкладками нашего конденсатора. Такое поле, как мы видели, возникает без всякого тока проводимости.
Сам Максвелл говорил, «что электрическое поле возникает во всех точках пространства, в которых имеется меняюшееся со временем магнитное поле, независимо от того, есть ли в них проводник или нет». Согласно представлениям Максвелла, проводник в котором появляется э.д.с., служит только тем обьектом в котором электрические силы себя проявляют. (Курс Общей Физики, С.Э. Фриш и А.В. Тиморева, Москва 1959, Стр. 466)
Чтобы создать такое вихревое поле Максвелла без проводника, и, следовательно, без тока проводимости мы будем вращать дипольные заряды.
Рис. 1
Рис. 2
На других примерах вращения того же самого диполя, я покажу как в точке С колебания по величине одной из напряженностей +Е или -Е могут быть практически близки к нулю, хотя величина напряженности ей противоположная колеблется в прежних пределах от максимума до минимума.
Рис. 3
Максимальная величина отрицательной напряженности в точке С в этом случае меняться не будет, потому что отрицательный заряд — q находится в центре вращения, но зато будет меняться величина напряженности +Е от минимума до максимума, потому что наш заряд +q, то приближается к точке С то удаляется от нее. График этого колебания приведен на рис.4
Рис. 5
Минимальная величина положительной напряженности в точке С в этом случае меняться не будет, потому что заряд +q находится в центре вращения, но зато будет меняться величина напряженности -Е от максимума до минимума и наоборот, потому что наш заряд -q, то удаляется от точки С то приближается к ней. График этого колебания приведен на рис.6
Рис. 6
Природные источники вихревых полей Максвелла
Такие дипольные заряды существуют и в природе. Например в атомах вещества, где отрицательные заряды, электроны, вращаются вокруг положительного заряда ядра. Наиболее распространенным элементом в нашей галактике, млечный путь, является атом водорода. Он же является основным химическим элементом на солнце, благодаря которому происходят там термоядерные реакции.
Частота колебаний таких вихревых полей, как я уже сказал, зависит от периода обращения данного электрона вокруг ядра. Но физикам известно, что электрон в атоме водорода может иметь около или более 1000 стационарных орбит, поэтому периоды обращения электрона в атоме могут иметь около или более 1000 значений. По этой же причине и частота колебаний вихревого поля атома водорода имеет столько же значений.
Но вихревые поля могут существовать и на уровне ядра атома, потому что само ядро атома представляет собой один из вращающихся диполей, которые мы разобрали вначале этой статьи. Например, протон состоит из противоположных по знаку кварков, которые вращаются, подобно нашему диполю, хотя бы потому что протон вращается в ядре атома и т.д.. Таким образом все пространство солнечной системы и других звездных систем представляет из себя вихревое поле Максвелла.
Положительные и отрицательные переменные электрические и магнитные поля
Положительная и отрицательная энергия вихревого поля
Вихревое поле и свободная энергия
Гипотеза максвелла о вихревом электрическом поле
Теория Д.К. Максвелла лежит в основе объяснения существования и свойств любых электромагнитных волн, таких, как световые волны, радиоволны, инфракрасное и ультрафиолетовое излучения. Эта теория является феноменологической, т.е. в ней не рассматриваются молекулярное строение среды и внутренний механизм процессов, происходящих в среде под действием электрического и магнитного полей. Электрические и магнитные свойства среды характеризуются относительной диэлектрической проницаемостью ε, относительной магнитной проницаемостью m и удельной электрической проводимостью σ. Предполагается, что эти параметры среды определяются из эксперимента.
Дифференциальные уравнения Максвелла получаются из интегральных с помощью двух теорем векторного анализа: теоремы Остроградского-Гаусса и теоремы Стокса.
Операция дивергенции над произвольным вектором сводится к пространственной производной вида:
| (4.1.2) |
Векторная операция rot в декартовых координатах выражается так:
| (4.1.4) |
Первое уравнение Максвелла
Это уравнение представляет собой обобщение закона электромагнитной индукции Фарадея:
| (4.1.5) |
Однако для произвольного контура выполняется взаимосвязь:
| (4.1.6) |
Сравнивая (4.1.5) и (4.1.7) с учетом (4.1.6), для произвольного контура L, мысленно проведенного в переменном магнитном поле, можно записать:
| (4.1.8) |
Используя теорему Стокса, преобразуем (4.1.5):
| (4.1.9) |
Сравнивая подинтегральные выражения в (4.1.7) и в правой части (4.1.9), получим окончательно первое уравнение Максвелла в дифференциальной форме:
| (4.1.10) |
Физический смысл этого уравнения: переменное магнитное поле индуцирует вихревое электрическое поле.
Второе уравнение Максвелла
Используем теорему Гаусса для диэлектриков:
| (4.1.11) |
Продифференцируем (4.1.11) по времени:
| (4.1.12) |
Правая часть этой формулы имеет размерность тока, следовательно, величина имеет размерность плотности тока. Максвелл предложил назвать эту величину плотностью тока смещения :
| (4.1.14) |
Введя представление о токе смещения, Максвелл по-новому подошел к рассмотрению условия замкнутости цепей электрического тока. Как известно, цепи постоянного тока должны быть замкнутыми. Однако для цепей переменного тока это условие уже не является обязательным. Например, при зарядке и разрядке конденсатора постоянный электрический ток протекает по проводнику, соединяющему обкладки, но не проходит через диэлектрик, находящийся между обкладками. Следовательно, цепь не замкнута. Однако, с точки зрения Максвелла, для переменного тока такая цепь замыкается благодаря току смещения, который протекает через такой участок, где нет проводника, т.е. через диэлектрик. На таком участке благодаря наличию переменного тока смещения обязательно возникает переменное магнитное поле. Однако действие тока смещения, приводящее к возникновению магнитного поля, нельзя отделить от действия обычного тока проводимости. Например, для прямолинейного тока проводимости можно записать:
| (4.1.15) |
Линии магнитного поля направлены по касательным к концентрическим окружностям, окружающим проводник с током. Найдем циркуляцию магнитного поля по замкнутому контуру в виде окружности радиуса r:
| (4.1.16) |
Максвелл предположил, что в правой части соотношения (4.1.16) следует добавить ток смещения:
| (4.1.17) |
где ток смещения легко вычислить, используя (4.1.14):
| (4.1.18) |
Силу тока проводимости можно также представить в виде:
| (4.1.19) |
Согласно теореме Стокса для магнитного поля, имеем:
| (4.1.20) |
Подставляя (4.1.18) и (4.1.19) в (4.1.17) и сравнивая подинтегральные выражения в правой и левой частях, получаем второе уравнение Максвелла:
| (4.1.21) |
При отсутствии тока проводимости, тем не менее, может существовать переменное магнитное поле, обусловленное только током смещения:
| (4.1.22) |
Третье уравнение Максвелла
Максвелл обобщил теорему Гаусса для диэлектриков (4.1.11), предположив, что она справедлива для любого электрического поля, как стационарного, так и переменного. Запишем уравнение (4.1.11) в виде:
| (4.1.23) |
Тогда, используя теорему Остроградского-Гаусса для вектора электрической индукции, получим:
| (4.1.24) |
Сравнивая подинтегральные выражения в (4.1.23) и (4.1.24), получим третье уравнение Максвелла:
| (4.1.25) |
Четвертое уравнение Максвелла
Поскольку поток вектора магнитной индукции равен нулю:
| (4.1.26) |
то, используя теорему Остроградского-Гаусса для вектора магнитной индукции, легко получить четвертое уравнение Максвелла:
| (4.1.27) |
Такое равенство определяется отсутствием магнитных зарядов.
Итак, полная система уравнений Максвелла в дифференциальной форме включает в себя четыре дифференциальных уравнения:
| (4.1.28) |
В случае изотропных несегнетоэлектрических и неферромагнитных сред и макроскопических токов, подчиняющихся закону Ома, эти уравнения в системе СИ имеют вид:
| (4.1.29) |
4.1.2. Свойства электромагнитных волн
Существование электромагнитных волн непосредственно следует их уравнений Максвелла. Для области пространства, не содержащей свободных электрических зарядов и макроскопических токов, эти уравнения приобретают вид:
| (4.1.30) |
Используя материальные уравнения (4.1.29), эти уравнения можно представить в виде:
| (4.1.31) |
Если записать эти уравнения в проекциях на оси декартовой системы координат, то получим: