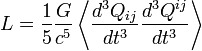гравитационное поле это в физике

Гравитационное поле это в физике

Все тела обладающие массой притягиваются друг к другу. Исаак Ньютон на основе многолетних данных астрономических наблюдений и законов динамики сформулировал закон всемирного тяготения : две любые материальные точки массами m 1 и m 2 притягиваются друг к другу вдоль линии соединяющей точки с силой прямо пропорциональной произведению масс точек и обратно пропорциональной квадрату расстояния (r) между ними:

Земля не является «материальной точкой» для тел, расположенных на ее поверхности. Теоретически доказано, что сила, с которой Земля притягивает тела, расположенные вне ее, равна силе, которую создавала бы материальная точка массой (М), равной массе Земли, и расположенная в центре Земли. Назовем силой тяжести силу, с которой тело взаимодействует с планетой, вблизи которой оно находится.

В соответствии с законом всемирного тяготения на материальную точку массой (m) со стороны Земли будет действовать сила тяжести, равная

Если тело движется с ускорением равным ускорению силы тяжести, то вес тела будет равен нулю:

1) вес тела равен нулю когда тело движется с ускорением равным ускорению силы тяжести ( ) в лифте вертикально вниз;

Закон всемирного тяготения определяет величину и направление силы всемирного тяготения, но не отвечает на вопрос как осуществляется это взаимодействие. Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения, или гравитационного поля.

1. Напряженность гравитационного поля ( ), силовая характеристика поля, равна силе, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой (это ничто иное как ускорение, с которым тело движется в поле тяготения):

Независимо от своей массы все тела под действием силы тяжести движутся с одинаковым ускорением ( )

Единица измерения [φ]=Дж/кг.

Потенциальная энергия тела в гравитационном поле равна:

Тогда работа гравитационного поля по перемещению тела из точки с потенциалом φ 1 в точку с потенциалом φ 2 равна:

Работа гравитационного поля по перемещению тела между двумя точками не зависит от траектории движения тела, а определяется только разностью потенциалов начальной и конечной точек, на замкнутом пути работа гравитационного поля равна нулю. То есть, сила всемирного тяготения и сила тяжести являются консервативными.

В качестве примера рассмотрим гравитационное поле материальной точки.

Наглядную картину поля представляет набор линий напряженности и эквипотенциальных поверхностей, например, гравитационное поле материальной точки представлено на рисунке (1.8.2).

Мы уже упоминали, что гравитационное поле Земли можно рассматривать, как поле материальной точки расположенной в центре Земли. Тогда потенциальная энергия тела, находящегося на высоте h относительно Земли:

Потенциальная энергия тела на высоте h над поверхностью Земли, равна:

Рассмотрим взаимосвязь между потенциалом и напряженностью поля тяготения.

Элементарная работа, совершаемая полем при малом перемещении тела массой (m), равна

Величина dφ/dl характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения, это ничто иное, как градиент потенциала.

Таким образом, напряженность гравитационного поля численно равна градиенту потенциала гравитационного поля и направлена в сторону его уменьшения:

На Земле приблизительно инерциальными являются системы отсчета, которые покоятся или движутся равномерно и прямолинейно относительно точек на поверхности Земли.

Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, рассматривают три варианта проявления этих сил.

1. Сила инерции возникает при ускоренном поступательном движении системы отсчета и направлена против вектора ускорения неинерциальной системы отсчета :

Действию центробежной силы инерции подвергаются пассажиры в движущемся транспорте на поворотах; летчики при выполнении фигур высшего пилотажа; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах, где они достигают огромных значений. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов) принимаются специальные меры для уравновешивания центробежных сил инерции.

равна произведению удвоенной массы тела на векторное произведение скорости поступательного движения тела относительно системы отсчета и угловой скорости вращения системы отсчета. Эта сила направлена перпендикулярно векторам скорости тела и угловой скорости вращения системы в соответствии с правилом правого винта.

Земля представляет собой вращающуюся систему отсчета и действие силы Кориолиса объясняет ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север (рис.1.8.4), то сила Кориолиса будет направлена вправо по отношению к направлению движения, и тело отклонится на восток. Если тело движется в юг, то сила Кориолиса также направлена вправо по отношению к направлению движения, и тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые. Аналогично можно показать, что в южном полушарии сила Кориолиса, действующая на движущиеся тела, будет направлена влево по отношению к направлению движения.

Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета : произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции):

Обратим еще раз внимание на то, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета, поэтому они не подчиняются третьему закону Ньютона. Два основных положения механики: 1) ускорение всегда вызывается силой; 2) сила всегда обусловлена взаимодействием между телами, в неинерциальных системах отсчета одновременно не выполняются.

Таким образом, силы инерции действуют только в неинерциальных системах отсчета, в инерциальных системах отсчета таких сил не существует.

Все тела независимо от их масс и химического состава, получают в данном гравитационном поле одинаковые ускорения. Поэтому в таком поле они движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают свободно движущиеся тела, если их движение рассматривать относительно какой-либо неинерциальной системы отсчета.

Силы инерции, действующие на тела неинерциальной системе отсчета, пропорциональны их массам и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в «поле сил инерции» эти тела движутся совершенно одинаково, если только одинаковы начальные условия.

Все механические явления и движения в лифте будут в точности такими же, что и в неподвижном лифте, висящем в поле тяжести.

Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции.

Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции.

Принципа эквивалентности Эйнштейна: все физические явления в поле сил тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы.

Принцип эквивалентности гравитационных сил и сил инерции можно рассматривать как принцип эквивалентности гравитационной и инерционной масс тела.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2013

Источник

Гравитационное поле

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Комплекс задач о взаимодействии многих тел достаточно обширный и является одним из базовых, далеко не полностью разрешённых, разделов механики. В рамках ньютоновской концепции проблема ветвится на.

Согласно концепции переме́нной ско́рости све́та (ПСС) считается, что скорость света в вакууме, обычно обозначаемая c, в некоторых случаях может не быть константой. В большинстве ситуаций в физике конденсированного состояния распространение света в среде действительно происходит с меньшей скоростью, чем в вакууме. Кроме того, в некоторых расчётах квантовой теории поля необходимо учитывать, что виртуальные фотоны должны двигаться на короткие расстояния в том числе со скоростью, отличной от скорости.

В физике, при рассмотрении нескольких систем отсчёта (СО), возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО).

В физике и математике, в отрасли динамических систем, двойной маятник — это маятник с другим маятником, прикреплённым к его концу. Двойной маятник является простой физической системой, которая проявляет разнообразное динамическое поведение со значительной зависимостью от начальных условий. Движение маятника руководствуется связанными обыкновенными дифференциальными уравнениями. Для некоторых энергий его движение является хаотическим.

Источник

Гравитационное поле Земли

Гравита́ция (всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела. По современным данным, является универсальным взаимодействием в том смысле, что, в отличие от любых других сил, всем без исключения телам независимо от их массы придаёт одинаковое ускорение. Главным образом гравитация играет определяющую роль в космических масштабах. Термин гравитация используется также как название раздела физики, изучающего гравитационное взаимодействие. Наиболее успешной современной физической теорией в классической физике, описывающей гравитацию, является общая теория относительности, квантовая теория гравитационного взаимодействия пока не построена.

Содержание

Гравитационное взаимодействие

.

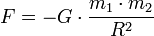
Здесь G — гравитационная постоянная, равная примерно 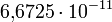м³/(кг•с²). Знак минус означает, что сила, действующая на тело, всегда равна по направлению радиус-вектору, направленному на тело, то есть гравитационное взаимодействие приводит всегда к притяжению любых тел.

Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося так же и при изучении излучений (см. например, Давление света), и являющимся прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.

Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в поле тяжести часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.

Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.

Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это тем не менее очень важная сила во Вселенной. Для сравнения: полный электрический заряд этих тел ноль, так как вещество в целом электрически нейтрально.

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. В античные времена Аристотель считал, что объекты с разной массой падают с разной скоростью. Только много позже Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

Небесная механика и некоторые её задачи

Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации называется небесной механикой.

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух тел в пустом пространстве. Эта задача решается аналитически до конца; результат её решения часто формулируют в виде трёх законов Кеплера.

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении, достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе, эта неустойчивость не позволяет предсказать движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений, и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — нетривиальная структура колец Сатурна.

Несмотря на попытки описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.

Сильные гравитационные поля

В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:

Гравитационное излучение

Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого до сих пор не подтверждено прямыми наблюдениями. Однако, имеются косвенные наблюдательные свидетельства в пользу его существования, а именно: потери энергии в двойной системе с пульсаром PSR B1913+16 — пульсаром Халса-Тейлора — хорошо согласуются с моделью, в которой эта энергия уносится гравитационным излучением.

где Q_ij — тензор квадрупольного момента распределения масс излучающей системы. Константа 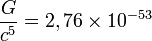(1/Вт) позволяет оценить порядок величины мощности излучения.

Начиная с 1969 года (эксперименты Вебера (англ.)) и до настоящего времени (февраль 2007) предпринимаются попытки прямого обнаружения гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (GEO 600), а также проект космического гравитационного детектора [2] республики Татарстан.

Тонкие эффекты гравитации

Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и их обнаружение и экспериментальная проверка поэтому весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.

Среди них, в частности, можно назвать увлечение инерциальных систем отсчета (или эффект Лензе-Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли, но его полные результаты пока не опубликованы.

Квантовая теория гравитации

Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена непротиворечивая перенормируемая квантовая теория. Впрочем, при низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2.

Стандартные теории гравитации

В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных экспериментальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.

Существует современная каноническая [3] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой (см. статью Альтернативные теории гравитации). Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.

Общая теория относительности

В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала) иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем или метрикой четырехмерного пространства-времени, а напряженность гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой. Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих метрику пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырехмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием ее формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка. Известно, что в ОТО имеются затруднения с объяснением факта неинвариантности энергии гравитационного поля, поскольку данная энергия не описывается тензором. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия. Считается, что существуют определенные проблемы с однозначностью результатов и обоснованием непротиворечивости. Однако экспериментально ОТО считается подтверждающейся до самого последнего времени. Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики, подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое в основном и доступно экспериментальной проверке.

Теория Эйнштейна-Картана

Теория Эйнштейна-Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина объектов. [4] В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана-Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к ОТО настолько малы, что пока не видно даже гипотетических путей для их измерения.

Релятивистская теория гравитации

Релятивистская теория гравитации (РТГ) разрабатывается академиком Логуновым А. А. с группой сотрудников. [5] В ряде работ они утверждают, что РТГ имеет следующие отличия от ОТО [6] :

Как и в ОТО, в РТГ под веществом понимаются все формы материи (включая и электромагнитное поле), за исключением самого гравитационного поля. Следствия из теории РТГ таковы: чёрных дыр как физических объектов, предсказываемых в ОТО, не существует; Вселенная плоская, однородная, изотропная, неподвижная и евклидовая.

C другой стороны, существуют не менее убедительные аргументы противников РТГ, сводящиеся к следующим положениям:

Теория Бранса — Дикке

В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ, относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум тензорным уравнениям для метрики. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля. [9]

Источник

ГРАВИТАЦИОННОЕ ПОЛЕ

Смотреть что такое «ГРАВИТАЦИОННОЕ ПОЛЕ» в других словарях:

ГРАВИТАЦИОННОЕ ПОЛЕ — (поле тяготения) поле физическое, создаваемое любыми физическими объектами; через гравитационное поле осуществляется гравитационное взаимодействие тел … Большой Энциклопедический словарь

ГРАВИТАЦИОННОЕ ПОЛЕ — ГРАВИТАЦИОННОЕ ПОЛЕ, пространство вокруг предмета, чья масса способна притягивать другой предмет. Сила этого притяжения, разделенная на массу второго предмета, и есть сила гравитационного поля. Предмет с большой массой, такой как Земля, имеет… … Научно-технический энциклопедический словарь

Гравитационное поле — (поле тяготения), один из видов поля физического, посредством которого осуществляется гравитационное взаимодействие (притяжение) тел, например Солнца и планет Солнечной системы, планет и их спутников, Земли и находящихся на ней или вблизи нее тел … Иллюстрированный энциклопедический словарь

ГРАВИТАЦИОННОЕ ПОЛЕ — (поле тяготения), (см. ТЯГОТЕНИЕ). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия

гравитационное поле — [ГОСТ 25645.103 84] Тематики условия физические косм. пространства EN gravity field … Справочник технического переводчика

Гравитационное поле — Гравитационное поле, или поле тяготения физическое поле, через которое осуществляется гравитационное взаимодействие[1]. Содержание 1 Гравитационное поле в классической физике … Википедия

гравитационное поле — (поле тяготения), поле физическое, создаваемое любыми физическими объектами; через гравитационное поле осуществляется гравитационное взаимодействие тел. * * * ГРАВИТАЦИОННОЕ ПОЛЕ ГРАВИТАЦИОННОЕ ПОЛЕ (поле тяготения), поле физическое (см. ПОЛЕ… … Энциклопедический словарь

гравитационное поле — gravitacijos laukas statusas T sritis Standartizacija ir metrologija apibrėžtis Klasikinės fizikos požiūriu – gravitacinės sąveikos tarpininkas, kai lauko šaltiniai yra sąveikaujančiųjų dalelių ar jų sistemų masės. Bendrosios reliatyvumo teorijos … Penkiakalbis aiškinamasis metrologijos terminų žodynas

гравитационное поле — gravitacijos laukas statusas T sritis fizika atitikmenys: angl. gravitational field vok. Gravitationsfeld, n; Schwerefeld, n rus. гравитационное поле, n; поле тяготения, n pranc. champ de gravitation, m; champ de pesanteur, m; champ… … Fizikos terminų žodynas

ГРАВИТАЦИОННОЕ ПОЛЕ — (поле тяготения), поле физическое, создаваемое любыми физ. объектами; через Г. п. осуществляется гравитац. взаимодействие тел … Естествознание. Энциклопедический словарь

Источник