как найти 30 градусов на полу
Калькулятор уклонов
Онлайн калькулятор
Посчитать уклон
Расстояние L =
Превышение h =
Посчитать превышение
Уклон α =
Расстояние L =
Посчитать расстояние
Уклон α =
Превышение h =
Теория
Как посчитать уклон
Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:
В процентах:
Уклон в % = h / L ⋅ 100
В промилле:
Уклон в ‰ = h / L ⋅ 1000
В градусах:
Уклон в ° = arctg ( h /L)
Пример
Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:
Уклон дороги = 30/500 ⋅ 100 = 6%
Как посчитать превышение
Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
h = L ⋅ Уклон в % /100
Если уклон в промилле (‰):
h = L ⋅ Уклон в ‰ /1000
Если уклон в градусах (°):
Пример
Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:
h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м
Как посчитать расстояние
Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
L = h / Уклон в % ⋅ 100
Если уклон в промилле (‰):
L = h / Уклон в ‰ ⋅ 1000
Если уклон в градусах (°):
Пример
Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:
Как отмерить угол 30 градусов на фанере без специальных инструментов?
В строительстве часто требуется отмерить угол в 90*, реже 45* и 30*. Не всегда есть под рукой необходимые инструменты. А углы-то нужны. Так как плотники народ изобретательный, появились способы построения углов при помощи метра или рулетки, которая всегда в наличии.
Начнём с построения прямого угла, от него проще построить все остальные.
Способ 3-4-5. Если соединить эти отрезки в треугольник, то угол образованный меж 3,4 будет прямым. Квадрат гипотенузы равен сумме квадратов катетов. 3*3 + 4*4= 25= 5*5. Отрезок можно брать какой удобно: в см, в метрах или 5 см, 20 см. Просто потом умножаем его на 3,4,5.
При отложении на катетах равных отрезков и соединяя гипотенузой точки, получаем 45*.
При отложении отрезков в соотношении 1/2 получаем 30* и 60*.
P.S. При расчётах стропил, чтоб на коньке получился прямой угол, берётся длина подстропильной балки делится на 7 и умножается на 5, получается угол максимально приближенный к прямому. 7*7=49 почти ровно 5*5+5*5=50.
Для этого берем гвоздик, рейку и карандашик. Проводим прямую линию, на чертеже штрих пунктирная линия, пробиваем рейку с гвоздем и фанерой по штрих пунктирной линии в любой его точке и используя рейку как циркуль чертим окружность любого диаметра, но этот же диаметр пригодится еще для одного круга который мя начертим на месте пересечения окружности и штрих пунктирной линии.
Есть разные способы, лучше всего использовать то, что найти можно без особых проблем. Тетрадь в клетку имеется у каждого, по крайней мере, ее можно купить без проблем. Нам понадобится один лист, в нем следует построить треугольник (прямоугольный), у которого один из катетов будет составлять одиннадцать клеток. От длины второго катета будет зависеть величина углов (острых) между гипотенузой и катетами. Рисуем горизонтальную линию (наш искомый 11-ти клеточный катет):
Есть еще показатели измерений по клеткам, если один катет будет на 4 клетки, а второй на 7 клеток (в сумме 11, кстати, клеток), то один из острых углов (меньший) будет те самые искомые 30 градусов равен, причем погрешность тут куда меньше 1/2 градуса.
Есть и такое математическое утверждение, что катет, который равен 1/2 гипотенузы, лежать будет напротив как-раз 30-ти градусного угла.
Будем исходить из условий задачи. Специального инструмента для измерения углов у нас нет. Вполне реальная ситуация. Возможно, подобная необходимость появилась внезапно. однако выйти из неё не так уж и сложно.
Поочерёдно рассмотрю несколько способов, позволяющих с минимальной погрешностью отмерить угол в 30 градусов. Материал при этом (фанера или ДВП, или картон и пр.) не имеет значения. Поскольку задавшийся целью измерения человек находится не в лесу в пасмурную погоду, то какие-то из нижеперечисленных вспомогательных предметов у него найдутся.
Углы 30, 45, 60, 90 градусов: наглядные, стихотворные, боевые, электрические, драматические, музыкальные
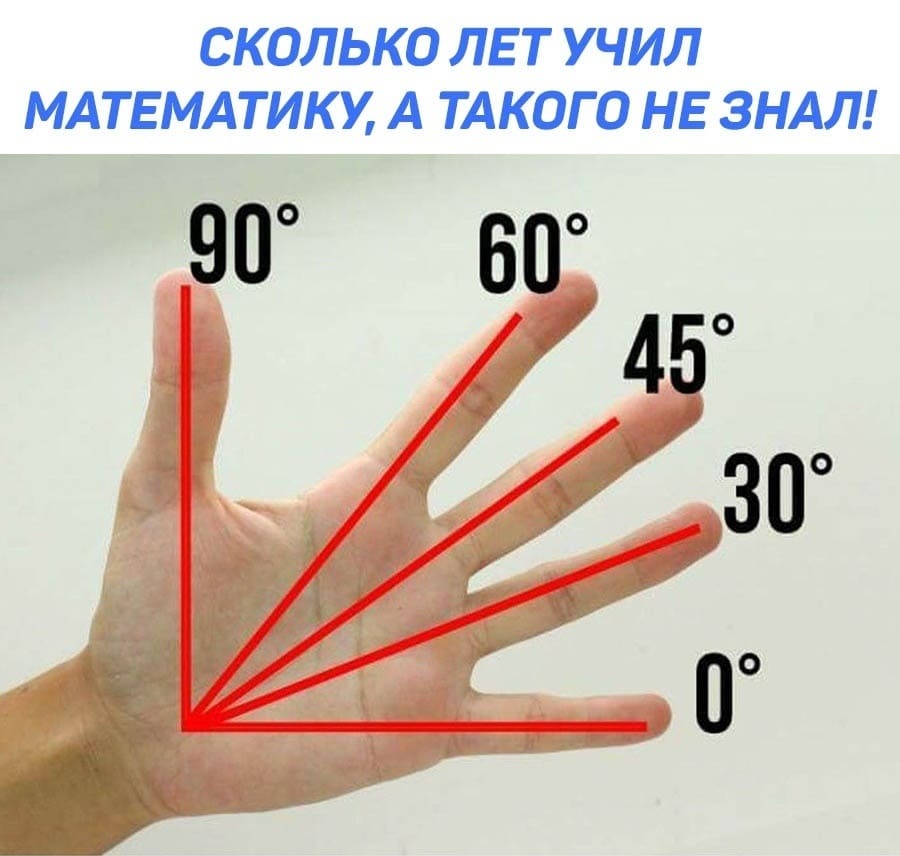
Можно определить углы 30, 45, 60, 90 градусов с помощью своей ладони.
Градусы наглядные: как их определить с помощью своей ладони
Наша рука, оказывается, очень даже может помочь с величинами углов, с градусами. Если посмотреть на нее под определенным углом зрения (см. рис. 1), то вот они, родимые: 0 градусов, 30, 45, 60 и даже 90 градусов!
Почему нам так важны именно эти величины? Почему нас могут интересовать углы 0, 30, 60 и 90 градусов, а также 45? Нет бы поинтересоваться, скажем, углами 15, 20, 75 или 80 градусов…
Оказывается, все дело в синусах и косинусах! Ибо синус нуля градусов есть ноль, а косинус 90 градусов — тоже равен нулю. Синус 30 градусов равен половинке единицы. Такое же значение 0,5 дает косинус 60 градусов.
А вот 45 градусов интересны тем, что синус и косинус 45 градусов равны между собой. Это значит, что тангенс 45 градусов будет равен единице. Ведь мы помним, что тангенс угла есть частное от деления синуса угла на косинус угла.
Но не только об этом хотелось сказать, глядя на рисунок…
Градусы стихотворные и число «пи»
Есть такое число – «пи». Оно почему-то равно 3,14. Хотя не совсем так. Это число с бесконечным количеством цифр после запятой. После запятой стоят не только цифры 1 и 4, но и множество других цифр.
Первый десяток цифр числа «пи» легко написать, если запомнить необычное стихотворение. Правда, стихи про «пи» нужно писать со старинной буквой «ять» — ведь и число «пи» очень старое, и стихотворение совсем не молодое:
Кто и шутя, и скоро пожелаетъ
Пи узнать число — ужъ знаетъ
Зачем в стихотворении стоит «ять» на конце? И при чем тут «пи»? Все очень просто: считаем буквы в словах стихотворения и подставляем цифры в число «пи».
Получается, кто=3, и=1, шутя=4, и=1, скоро=5 и так далее: 3,1415926536… Многоточие на конце — это значит, что есть продолжение цифрам, бесконечное продолжение.
Причем тут градусы? При том, что «пи» — это величина развернутого угла, но не в градусах, а в радианах (другая единица измерения величины угла). «Пи» радиан есть угол величиной 180 градусов.
Как говорят математики, отсюда нетрудно догадаться, что 0 градусов есть ноль радиан. 90 градусов есть «пи пополам» радиан. Нам этот термин «пи пополам» еще пригодится далее. Все остальные градусы таким же образом можно свести к разным частям числа «пи».
Получается, что мы теперь знаем стишок про 180 градусов — стишок про «пи»! Что это дает?
Градусы боевые: почему наши деды победили
Штурман откладывает карту в сторону. Достает маневренный планшет. Теперь он отслеживает на нем положение корабля относительно одного противника или сразу нескольких противников.
Тут — сплошные градусы. Кто из супостатов виден под каким углом? Угол есть решающая величина. Приходится учитывать как углы, так и их синусы, и косинусы.
Кто в школе учился, тот помнит, что синус и косинус угла не может быть больше единицы. Хоть что делай, больше единицы не получается.
А вот в годы войны у штурмана боевого корабля косинусы углов доходили порой до четырех! Потому и победили, что делали невозможное! Даже с косинусами, ограниченными правильной математикой!
Так что запомним вопреки математике: в годы войны косинусы углов могут доходить до «четырех». В том числе, поэтому наши деды победили!
Градусы электрические: отклонение между напряжением и током
Ну, синус? Ну, косинус? И что тут такого? Спросим любого человека, например, возле пивного ларька, что такое синус и как давно он пользовался косинусом после школы. Что услышим в ответ?! Во, именно «это» и услышим.
Вместе с тем мы постоянно живем, можно сказать, под градусом, точнее, под косинусом! Ежедневно мы пользуемся электричеством: нажимаем кнопки и выключатели, и дело с концом — все светится, крутится, работает.
Чтобы электричество выполняло свое предназначение, нужно электрическое напряжение и электрический ток. Обе «субстанции» должны быть вместе и одновременно. Но эти две величины могут иметь между собой угол отклонения, измеряемый «косинусом фи», как выражаются энергетики на своем профессиональном языке.
Если отклонение напряжения от тока есть ноль градусов, то электрическая мощность будет получена умножением величины напряжения на величину тока.
Допустим, подключаем электрообогреватель. Он начинает излучать тепло, равное по мощности этой самой величине: напряжение 220В (двести двадцать вольт) умножить на ток, скажем, 5А (пять ампер) равно 1КВт (1 киловатт) мощности. Становится тепло!
Если между напряжением и током есть отклонение, хотя бы на 1 градус, то придется перемножать не только напряжение и ток, но и полученный результат дополнительно умножать на косинус угла отклонения. Ноль градусов отклонения — косинус равен единице, умножение на единицу ничего не меняет. А вот косинус всего лишь 1-го градуса возможного отклонения уже меньше единицы. Не намного, но меньше. Это значит, что греть наша батарея будет уже слабее.
Чем больше отклонение электрического напряжения от электрического тока, чем будет больше между ними градусов так называемого угла «фи». Тем слабее будут греть батареи, хуже станет накал лампочек, и вообще будет меньше электричества.
И не говорите теперь, что косинус — это абстракция, которую мы оставили в школе навсегда…
Градусы драматические: косинус 90 градусов равен нулю
А что как напряжение и ток отклоняются друг от друга на 90 градусов?! Ведь косинус такого угла равен нулю. Умножение на ноль есть ноль. Это, что называется, страшный сон энергетиков — ужасная апокалиптическая драма!
Представьте себе, газ сжигается на тепловых электростанциях, вода крутит турбины на гидроэлектростанциях, нейтроны делятся в реакторах атомных электростанций. Ток «бежит» по проводам в дома. А там — косинус угла «фи» равен нулю — полный швах! Батареи не греют, лампочки не светятся, холодильники не работают.
Чтобы мысленный эксперимент с отклонением напряжения и тока на 90 градусов не стал реальностью, энергетики по всему миру постоянно следят за «косинусом фи». Денно и нощно, без устали, без перерывов.
Почему отклоняются напряжение и ток? Из-за потребителей электричества! Нет, не из-за домашних электрических обогревателей. И не из-за домашних лампочек накаливания. Но из-за оборудования заводов и фабрик.
Везде, где крутятся электромоторы, их «кручение» приводит как бы к обратному закручиванию электричества. Работающее оборудование возвращает энергетикам в электрические сети сдвинутое между собой напряжение и ток.
Образно говоря, чтобы крутить моторы, электричество должно «упираться» во что-то. И из-за этого понемногу «проворачивается» в обратную сторону. Что и приводит к возникновению угла сдвига между напряжением и током.
Если не следить за последствиями такого «сдвига», то угол между напряжением и током будет постоянно расти. Косинус фи начнет уменьшаться. Электростанции начнут работать сначала чуть-чуть вхолостую, потом все больше и больше, потом еще больше…
Градусы из радиоточки
Если напряжение и ток встанут друг относительно друга на 90 градусов — это будет недопустимое отклонение или «сдвиг по фазе на пи пополам»! Тогда электричество останется в проводах, но оно ничего не будет греть, освещать, двигать.
«Сдвиг по фазе на пи пополам» есть расхожее выражение, которое означает абсолютную неприемлемость того или иного действия, поступка.
Пришло оно к нам из того самого электротехнического «косинуса фи».
Про сдвиг между напряжением и током можно написать не одну драму с яркими событиями и участниками. Но мы не будем это делать, ибо наши энергетики не допустят подобного хода событий…
Кстати, кто помнит еще советское радио, что звучало практически в каждом доме? Там по утрам во многих городах сообщали не только про погоду. Погода — это тоже градусы, но другие.
Из радиоточки строго так говорили, обычно после прогноза погоды: «на сегодня режим энергопотребления установлен два тире два» или «. два тире один». Это про «наши» градусы, про «косинус фи»!
Что это за режимы такие: 2-2, 2-1 и другое? То были прямые указания предприятиям, как они должны именно сегодня компенсировать возникающие сдвиги между напряжением и током.
Энергетики шли к компенсирующим установкам и включали озвученные по радио режимы. Вот ведь насколько важны углы! Про них даже по центральному радио (с местным уклоном, разумеется) вещали ежедневно.
А вы говорите градусы, синусы, косинусы! И зачем мы их в школе «проходили», если вокруг нас их как не было, так и нет? Оказывается, были, есть и будут. Даже в обычной электрической розетке, в лампочке, в утюге.
Градусы музыкальные
Для тех, кто «добрался» до конца — маленький сюрприз: музыкальные «градусы». Вот как, оказывается, можно сыграть на фортепиано про число «пи» с точностью аж до 122 знаков после запятой. Музыка «развернутого угла 180 градусов»!
Словами добавить нечего, достаточно послушать. И все это про «пи» и про градусы, которые в школе «прошли» и забыли: