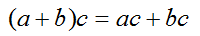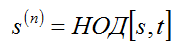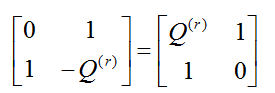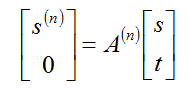как найти обратный элемент в поле

Обратный по модулю в кольце

Обратный по модулю

Калькулятор онлайн для вычисления обратного элемента по модулю в кольце. Алгоритм поддерживает работу с большими числами с некоторыми ограничениями.

Использование:

Заполняются два поля — число a и модуль m. Число a — число к которому ищем обратный, m — модуль, по которому ищем.

Калькулятор выдает обратный элемент после нажатия на кнопку «Вычислить».

Если установлена галочка «подробнее», то калькулятор помимо обратного элемента по модулю выдает некоторые этапы вычисления.

Ограничения:

Калькулятор поддерживает работу с большими целыми числами (в том числе отрицательными числами для числа a, и только положительными для модулю m) длиной не более 10 000 символов.

Что значит по модулю?

Синонимом к данному выражению является выражение «остаток от деления«. То есть выражение «5 по модулю 3» эквивалентно выражению «остаток от деления 5 на 3». И в том и в другом случае подразумевается в ответе число 2, так как остаток от деления 5 на 3 = 2.

Стоить отметить тот факт, что по модулю m мы имеем числа от 0 до m — 1. Действительно, остаток от деления на m никогда не превысит m — 1.

Что такое обратное?

Напомним, что число, умноженное на его обратное, равно 1. Из базовой арифметики мы знаем, что:

Число, обратное к числу A, равно 1 / A, поскольку A * (1 / A) = 1 (например, значение, обратное к 5, равно 1/5).
Все действительные числа, кроме 0, имеют обратную
Умножение числа на обратное к A эквивалентно делению на A (например, 10/5 соответствует 10 * 1/5)

Что такое обратное по модулю?

В модульной арифметике у нас нет операции деления. Тем не менее, у нас есть модульные инверсии.

Как найти модульный обратный

Наивный метод нахождения модульного обратного a ( по модулю m) является:
Шаг 1. Рассчитать a * b mod m для значений b от 0 до m — 1
Шаг 2. Модульная инверсия a mod m — это значение b, при котором a * b mod m = 1

Обратите внимание, что термин b mod m может иметь только целочисленное значение от 0 до m — 1, поэтому тестирование больших значений чем (m-1) для b является излишним.

Вы наверно уже догадались, что наивный метод является очень медленным. Перебор всех чисел от 0 до m-1 для большого модуля довольно-таки трудоемкая задача. Существует гораздо более быстрый метод нахождения инверсии a (mod m). Таковым является расширенный алгоритм Евклида, который реализован в данном калькуляторе.

Расширенный алгоритм Евклида

Представим наибольший общий делитель числа a и модуля m в виде ax + my. То есть НОД(a, m) = ax + my. Помним, что обратный элемент существует только тогда, когда a и m взаимно просты, то есть их НОД(a, m) = 1. Отсюда: ax + my = 1 — линейное диофантово уравнение второго порядка. Необходимо решить данное уравнение в целых числах и найти x, y.

Найденный коэффициент x будет являться обратным элементом к a по модулю m. Это следует оттуда, что, если мы возьмём от обеих частей уравнения остаток по модулю m, то получим: ax = 1 (m).

Расширенный алгоритм Евклида, в отличие от классического, помимо наибольшего общего делителя позволяет найти также коэффициенты x, y.

Алгоритм:

Выход : d, x, y, такие что d = gcd(a, m) = ax + my

3. [Выход] Вернуть (d, x, y) = (a₀, x₀, y₀)

Непонятен алгоритм? Ничего страшного, примеры ниже именно для этого и предназначены.

Пример для наивного метода.

Пусть a = 3, m = 7. То есть нам необходимо найти обратный элемент к 3 по модулю 7.

3 * 0 ≡ 0 (mod 7) — не подходит
3 * 1 ≡ 3 (mod 7)
3 * 2 ≡ 6 (mod 7)
3 * 3 ≡ 9 ≡ 2 (mod 7)
3 * 4 ≡ 12 ≡ 5 (mod 7)
3 * 5 ≡ 15 (mod 7) ≡ 1 (mod 7) Пример на расширенный алгоритм Евклида.

Пусть аналогично предыдущему примеру имеем a = 3, m = 7. Также, требуется найти обратный элемент к 3 по модулю 7. Согласно алгоритму начинаем заполнять таблицу на каждом этапе цикла.

Итерация	q	a0	a1	x0	x1	y0	y1
0	—	3	7	1	0	0	1
1	0	7	3	0	1	1	0
2	2	3	1	1	-2	0	1
3	3	1	0	-2	0	1	-3

После 3-ей итерации получили a1 = 0, строго по алгоритму из раздела «Теория» заканчиваем работу алгоритма.

Делаем проверку:

3 * (-2) + 7 * 1 = 1
-6 + 7 = 1
1 = 1 — верно!

Источник

Дискретная математика. KursRab. Мультипликативно-обратные элементы в поле вычетов

Пояснительная записка к курсовой работе

по дискретной математике.

Мультипликативно обратные элементы в поле вычетов.

СОДЕРЖАНИЕ

ПРОВЕДЕНИЕ АНАЛИЗА СВОЙСТВ, ХАРАКТЕРИЗУЮЩИХ ЗАДАННУЮ ТЕМУ

Полем называется множество с двумя определёнными операциями — сложением и умножением, причем имеют место следующие аксиомы:

Поле с конечным числом элементов называют полями Галуа GF(q).

Для представителей можно ввести операции сложения и умножения по mod(4):

0	1	2	3	0	1	2	3
0	0	1	2	3	0	0	0	0	0
1	1	0	3	2	1	0	1	2	3
2	2	3	0	1	2	0	2	3	1
3	3	2	1	0	3	0	3	1	2

Наибольший общий делитель двух заданных положительных чисел s и t может быть вычислен с помощью итеративного применения алгоритма деления. Эта процедура известна как алгоритм Евклида. Предположим, что t (1) t+t (1)

где остановка процесса наступает при получении нулевого остатка. Последний ненулевой остаток t ( n) равен наибольшему общему делителю. Этот факт будет доказан в следующей теореме. Матричные обозначения позволяют кратко записать шаги алгоритма Евклида в виде:

Теорема. (Алгоритм Евклида).[2][3] Для двух заданных положительных чисел s и t, где s>t, пусть s (0) =s и t (0) =t. Решение рекуррентных уравнений:

при r=1, …, n даётся величиной

где n равно наименьшему целому числу, для которого t ( n) =0.

Так как t ( r+1) ( r) и все остатки неотрицательны, то в конце концов наступит n, для которого t ( n) =0, так что завершение работы алгоритма произойдёт обязательно, легко проверить, что

так что s ( n) должно делить оба числа s и t и, следовательно, делит НОД[s, t]. Далее

Это завершает доказательство.

Из этой теоремы вытекает несколько важных следствий. Пусть

Тогда получаем следствие:

Для любых чисел s и t найдутся такие целые числа a и b, что

Достаточно доказать следствие для положительных s и t. Так как

и s ( n) =НОД[s, t], то утверждение выполняется при и .

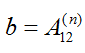
Следствие 2:

Получаемые в процессе алгоритма Евклида матричные элементы 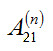и удовлетворяют равенствам:

Используя выписанные выше выражения для обратной матрицы и обращая первое равенство из доказательства прошлого следствия получаем

Утверждение вытекает отсюда непосредственно.

Доказательство.

Нахождение обратных элементов с использованием алгоритма Евклида[1]

Так как у поля модуль m – простое число, то для нахождения обратного элемента для элемента x можно найти уравнение ax+my=1. Тогда слагаемое my равно нулю (вычисления производятся по модулю m). Следовательно, элемент a является обратным к элементу x.

Нахождения обратных чисел можно реализовать с помощью малой теоремы Ферма.

ВЫВОДЫ

В соответствии с вышеописанными теоремами программа должна находить обратный элемент используя малую теорему Ферма или алгоритм Евклида. Программа должна работать для достаточно широкого спектра значений модуля, по которому производятся вычисления и элемента для которого вычисляется обратный элемент. То есть программа не должна вычислять обратный элемент, например, только для чисел, которые меньше 3 или 5 (для этих чисел обратный элемент в поле вычетов по такому маленькому модулю можно вычислить и без компьютера). То есть программа должна быть предназначена для вычисления обратного элемента для достаточно большого (в разумных пределах) числа. Также программа должна проверять корректность входных данных. То есть, в случае, если НОД введённого модуля и элемента должно равняться единице, в противном случае программа должна сообщать, о том, что данный элемент не имеет обратного.

ПОСТРОЕНИЕ ПРОГРАММНОЙ МОДЕЛИ

Напишем программу нахождения обратного числа для данного элемента в данном поле.

Поле возьмём по модулю простого числа.

Выбор метода

По началу кажется, что нахождение обратных элементов в поле проще всего реализовать с помощью малой теоремы Ферма. Но на практике из-за ограниченности разрядной сетки машины этот алгоритм использовать достаточно затруднительно. Например, для вычисления обратного элемента для 9 в поле по модулю 23:

9 21 =109418989131512359209.

Можно приводить числа по данному модулю после каждого умножения, что решит эту проблему для не очень больших чисел. Но для достаточно больших чисел эта проблема останется.

Причём значение имеет даже последняя девятка. хранения такого большого числа в компьютере и выполнения с ним операций вызывает определённые трудности. Следовательно, лучше реализовать алгоритм Евклида, работающий со стандартными типами данных, хотя для некоторых случаев (при небольших числах) алгоритм, построенный на следствии малой теоремы Ферма будет подходить больше.

Построение алгоритма программы

Напишем программу, реализующую нахождение обратного элемента с использованием алгоритма Евклида. По алгоритму Евклида (учитывая, что НОД[a, m]=1) выполняются следующие соотношения:

Для нахождения уравнения ax+my=1 выразим с помощью предпоследнего уравнения число 1 через t ( n-1) и t ( n-2) :

1= t (n-1) — Q (n+1) * (t (n-2)- Q (n) t (n-1) )

1= (1+Q (n+1) *Q (n) )*t (n-1) — Q (n+1) *t (n-2)

1= — Q (n+1) *t (n-2) + (1+Q (n+1) *Q (n) )*t (n-1)

Как отсюда видно множитель — Q ( n+1) «перешёл» из правого слагаемого (из слагаемого с большим) в левое слагаемое (с меньшим индексом). Проверим дальше. Теперь выразим 1 через t ( n-2) и t ( n-3) :

1= — Q (n+1) *t (n-2) + (1+Q (n+1) *Q (n) )*t (n-1)

1= — Q (n+1) *t (n-2) + (1+Q (n+1) *Q (n) )*( t (n-3) — Q (n-1) t (n-2) )

1= (1+Q (n+1) *Q (n) )*t (n-3) + ((1+Q (n+1) *Q (n) )*( — Q (n-1) ) — Q (n+1) )t (n-2) (1)

Как видно снова множитель из правого слагаемого перешёл в левое слагаемое. Правое слагаемое составилось из прошлого множителя правого слагаемого, умноженного на следующее частное, и прошлого левого слагаемого. То есть, если на данном шаге перед слагаемым t с меньшим индексом стоит множитель a, а перед другим слагаемым – b, то для следующего шага перед слагаемым с меньшим индексом будет стоять b, а перед другим слагаемым b*a-a.

Графическая схема алгоритма, осуществляющего нахождение НОД с помощью алгоритма Евклида:

Этот алгоритм при использовании для нахождения обратных элементов в качестве числа t должен получать модуль в котором производить вычисления, а в качестве числа s элемент, для которого необходимо найти обратный элемент. Тогда в выходной переменной s2 будет получаться обратный элемент для числа s. Естественно при получении входных данных модуль t должен быть таким, что полученная структура была бы полем. То есть число t должно быть простым. (когда t – простое, то НОД[t, s]=1 и в полученном выражении слагаемое с t сокращается).

Составление программы на BORLANDC++3.1

Для хранения модуля и введённого числа подходит тип long (для того, чтобы программа могла работать с более длинными числами).

Для реализации стека был составлен специальный модуль, в котором были реализованы стандартные процедуры работы со стеком (PUSH (добавление элемента в стек), POP (извлечение элемента из стека), EMPTY (проверка стека на пустоту)).

С использованием стека была разработана процедура, вычисляющая с помощью алгоритма Евклида НОД двух чисел и возвращающая также полученное уравнение.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Для проверки работоспособности программы достаточно вычисленный обратный элемент умножить на данный элемент и взять остаток от деления полученного числа на модуль, по которому производились вычисления. Если получится единица, то обратный элемент вычислен верно. Для сравнения были произведены вычисления с использованием малой теоремы Ферма и калькулятора.

(элемент, для которого находится обратный эдемент)m

(модуль, по которому производятся вычисления)a m-2a ( m-2) (mod(m))

92310941898913151235920918181258331561011,176561609770433870981098575571e+1739292199910013,6806348825922326789470084006052e+2996720500для вычисленного вручную:

для вычисленного с помощью программы:

1111130001не удалось вычислитьне удалось вычислить22494177777100001не удалось вычислитьне удалось вычислить35714145557653765не удалось вычислитьне удалось вычислитьне существует обратного элемента—34453310000001не удалось вычислитьне удалось вычислить1644429144256323843553333не удалось вычислитьне удалось вычислить7591774391

Как видно в таблице весь последний столбец занят единицами, кроме той строки, для которой не существует обратного элемента. Следовательно, программа работает верно.

ВЫВОДЫ ПО ВСЕЙ КУРСОВОЙ РАБОТЕ

Анализируя составленную программу можно сделать вывод, что с помощью алгоритма Евклида можно достаточно быстро найти обратный к данному элемент по данному модулю. При тестировании программы работала с числами около одного или двух миллиардов практически мгновенно. Никакого замедления не было замечено.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

Источник

Операции по модулю

Математические термины

Во всём последующем материале никак не фигурирует понятие “модуль числа” в привычном смысле (\(\lvert x \rvert\)). Речь идёт о “сравнении по модулю”. Если вы не знакомы с этим понятием, вкратце сравнение по модулю выглядит следующим образом:

Это читается “\(a\) сравнимо с \(b\) по модулю \(m\)”, и в привычных для информатики терминах обозначает следующее:

\[a \bmod m = b \bmod m,\]

Поле по модулю

Можно сказать, что в таких задачах мы оперируем не числами, а их остатками от деления на 1000000007. Это возможно благодаря следующим свойствам вычислений с остатком:

Доказательство возможности сложения, вычитания и умножения по модулю

Для начала докажем достаточно очевидное утверждение:

\[\forall n \in \mathbb: x \bmod m = (x + nm) \bmod m.\]

Значит, по определению сравнимости, \(\forall n \in \mathbb: x \equiv x + nm \pmod\), что и требовалось доказать.

\[(a + b) \bmod m = \\ = (xm + a \bmod m + ym + b \bmod m) \bmod m = \\ = (a \bmod m + b \bmod m + m(x + y)) \bmod m, = \\ = (a \bmod m + b \bmod m) \bmod m,\]

что и требовалось доказать.

Вычитание и умножение доказываются похожим образом:

Пример: вычисление факториала по модулю

В качестве примера, вычислим значение \(10^8!\) по модулю \(10^9 + 7\):

Как видите, на практике вычисления в поле по модулю отличаются от обычных лишь наличием взятия всех промежуточных результатов по модулю (строка 8). Однако существует два момента, которые нужно всегда учитывать для избежания ошибок:

Возведение в степень по модулю. Бинарное возведение в степень

Возможность умножения по модулю позволяет нам естественным образом возводить числа в различные степени по модулю. При операциях в поле по модулю степени часто сильно превышают привычные значения, и тривиальный алгоритм с линейным временем работы оказывается неприменимым. В таких ситуациях чаще всего используется алгоритм бинарного возведения в степень.

Алгоритм бинарного возведения в степень достаточно лаконичен. Его идея заключается в том, чтобы использовать возведение в квадрат промежуточных результатов, когда это возможно. Используется следующее очевидное свойство:

Таким образом засчёт одной операции умножения можно уменьшить степень вдвое. Если же текущая степень нечётная, то можно просто уменьшить её на единицу простым умножением, и получить чётную.

Простой рекурсивный вариант на C++:

Можно заметить, что в худшем случае на каждом втором вызове функции степень будет уменьшаться вдвое. Значит, время работы алгоритма можно оценить как \(O(\log p)\).

Разумеется, бинарное возведение в степень можно использовать и без модуля, но степени в таких случаях слишком малы, чтобы заметить разницу в скорости.

Деление в поле по модулю

К сожалению, деление не так легко адаптируется к полю по модулю, как другие арифметические операции. В этом разделе описывается один из способов деления по модулю, но не приводится его доказательство, так как оно значительно усложнило бы эту лекцию.

Деление по модулю определяется через умножение следующим образом:

Ключевую роль играет значение \(b^<-1>\), называющееся обратный элемент в поле по модулю. Оно никак не связано с классическим понятием обратного числа, хотя бы тем, что всегда является целым (так как в поле по модулю существуют только целые числа). Для обратного элемента должно выполняться следующее условие:

Например, обратным элементов в поле по модулю \(1000000007\) для числа \(2\) является число \(500000004\), так как \((2 * 500000004) \bmod 1000000007 = 1\). Следовательно, в поле по модулю \(1000000007\) делению на \(2\) соответствует умножение на \(500000004\)

Алгоритм нахождения обратного элемента в поле по простому модулю достаточно прост (в реализации) и выражается следующей формулой:

Как можно заметить, число \(x\) возводится в достаточно большую степень, и линейный алгоритм в этой ситуации не подойдёт. Вот и пример необходимости использования бинарного возведения в степень по модулю.

Стоит заметить что из-за использования бинарного возведения в степень, деление по модулю имеет сложность \(O(\log m)\), тогда как все остальные арифметические операции по модулю работают за \(O(1)\).

Источник