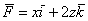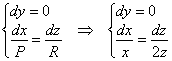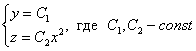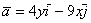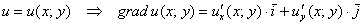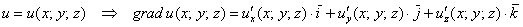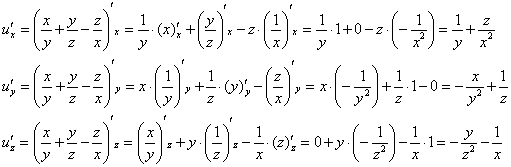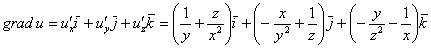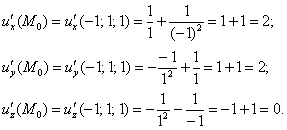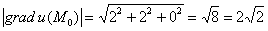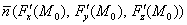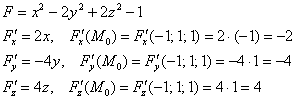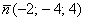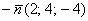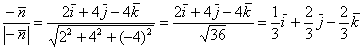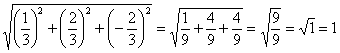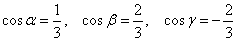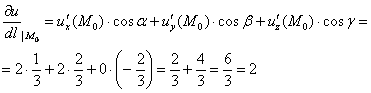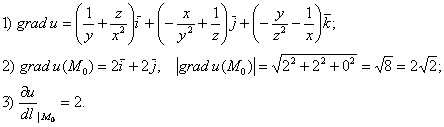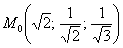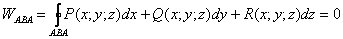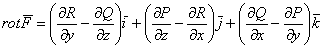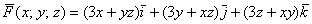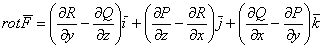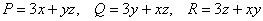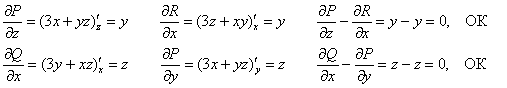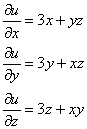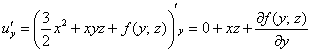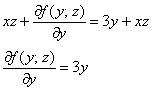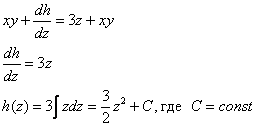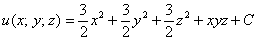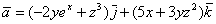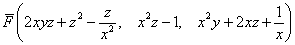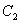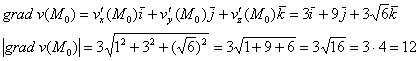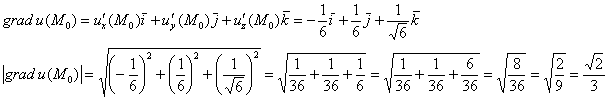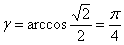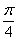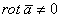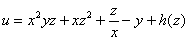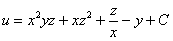как задается векторное поле
Теория поля
Известная также, как векторный анализ. А кому-то векторный анализ, известный как теория поля =) Наконец-то мы добрались до этой интереснейшей темы! Данный раздел высшей математики язык не поворачивается назвать простым, однако ж, в грядущих статьях я постараюсь достигнуть двух целей:
а) чтобы все понимали, о чём вообще идёт разговор;
б) и чтобы «чайники» научились решать, как минимум, простые вещи – хотя бы на уровне заданий, которые предлагаются студентам-заочникам.
Весь материал будет изложен в популярном стиле, и если вам нужна более строгая и полная информация, то можно взять, например, 3-й том Фихтенгольца или заглянуть в Вики.
И сразу расшифруем заголовок. С теорией, думаю, всё понятно – в лучших традициях сайта мы разберём её основы и сделаем основной упор на практику. Ну а с чем у вас ассоциируется слово «поле»?
Поле с травой, футбольное поле…. Ещё? Поле деятельности, поле экспериментов. Приветствую гуманитариев! …Из школьного курса? Электрическое поле, магнитное, электромагнитное…, так, хорошо. Гравитационное поле Земли, в котором мы находимся. Отлично! Так, кто это там сказал о поле действительных и комплексных чисел? …совсем какие-то монстры здесь собрались! =) Благо, алгебра уже пройдена.
На ближайших уроках мы познакомимся со специфическим понятием поля, конкретными примерами из жизни, а также научимся решать тематические задачи векторного анализа. Теорию поля лучше всего изучать, как вы правильно догадываетесь, на поле – природе, где есть лес, речка, озеро, деревенский домик, и я приглашаю всех погрузиться если и не в тёплую летнюю реальность, то в приятные воспоминания:
ПолЯ в рассматриваемом сегодня смысле бывают скалярные и векторные, и начнём мы с их «кирпичиков».
Во-первых, скаляр. Довольно-таки часто этот термин ошибочно отождествляют с числом. Нет, всё обстоит немного не так: скаляр – это величина, каждое значение которой может быть выражено лишь одним числом. В физике примеров масса: длина, ширина, площадь, объём, плотность, температура и др. Всё это скалярные величины. И, кстати, масса – тоже пример.
Во-вторых, вектор. Алгебраического определения вектора я коснулся на уроке о линейных преобразованиях и одну из его частных ипостасей не знать просто невозможно =) Типичный вектор выражается двумя или бОльшим количеством чисел (своими координатами). И даже для одномерного вектора лишь одного числа не достаточно – по той причине, что у вектора есть ещё направление. И точка приложения, если вектор не свободен. Векторами характеризуют силовые физические поля, скорость и многие другие величины.
Ну что же, теперь можно приступить к сбору алюминиевых огурцов урожая:
Скалярное поле
Если каждой точке 
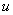
Рассмотрим, например, исходящий из земли перпендикулярный луч. Воткните для наглядности лопату =) Какие скалярные поля можно задать на этом луче? Первое, что напрашивается – это поле высоты – когда каждой точке 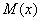
Теперь подойдём к озеру и мысленно проведём над его поверхностью плоскость. Если каждой точке 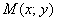
Важнейшим свойством скалярного поля является его инвариантность относительно системы координат. Если перевести на человеческий язык, то с какой бы стороны мы на лопату / озеро ни посмотрели – скалярное поле (высота, глубина, температура и т.д.) от этого не изменятся. Более того, скалярное поле, скажем, глубины можно ведь задать и на другой поверхности, например, на подходящей полусфере, или непосредственно на самой водной поверхности. А почему нет? Разве нельзя каждой точке полусферы, расположенной над озером, поставить в соответствие число? Плоскость я предложил исключительно ради удобства.
Добавим ещё одну координату. Возьмите в руку камень. Каждой точке 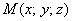
С чисто математической точки зрения (вне физического или другого частного смысла) скалярные поля традиционно задают нашими «обычным» функциями одной 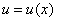
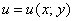
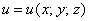
Так, линии уровня глубины озера представляют собой замкнутые непересекающиеся линии на плоскости. Каждая из этих линий соответствует определённому значению глубины, и по соответствующей «плоской» карте мы можем судить о рельефе дна – где мелководье, где «обрывы» и т.д.
Поверхности уровня представляют собой непересекающиеся пространственные поверхности, «вложенные» друг в друга. Или «лежащие» друг на друге. Или… у кого на что фантазии хватит =) Каждой такой поверхности соответствует постоянное значение скалярного поля, например, какая-то конкретная температура.
Однако наши «обычные» числа и функции задают скалярные поля далеко не всегда! Приведу классический пример с вектором – для определённости рассмотрим геометрический вектор плоскости 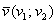
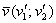
Координаты вектора – это числа? Числа. Но скалярными величинами они не являются! Поскольку скаляры не зависят от системы координат. Более того, координаты векторов можно ведь задать и «обычными» функциями – и эти функции не будут порождать скалярное поле!
Надо сказать, ловким получился переход к следующему параграфу:
Векторное поле
Если каждой точке 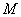
Из чего следует, что элементы векторного поля не свободны, то есть «привязаны» к точкам. И почему векторы в «неволе» – становится ясно из простых примеров. В частности, на уроке о криволинейных интегралах по замкнутому контуру мы провели «плоский» опыт с магнитом на столе: чем ближе к магниту поднести железку, тем сильнее она притягивается. И эта сила в той или иной точке поверхности стола как раз характеризуется вектором напряжённости магнитного поля. Чем сильнее притяжение, тем длиннее вектор, ну и его остриё, понятно, указывает направление действия силы.
Но гораздо чаще векторные поля рассматривают в трёхмерном пространстве, пожалуйста: наша Земля – тот же больший магнит. Другой пример – её гравитационное поле. Чем дальше от поверхности, тем меньше сила тяжести и тем короче соответствующие силовые векторы. Кстати, куда они «смотрят»? Говоря просто, все они направлены к центру нашей планеты.
Большую группу векторных полей образуют так называемые поля скоростей. Посмотрите на поле (которое с травкой) и мысленно очертите над ним произвольную пространственную область. Представьте, что над полем дует ветер – небольшой такой ураганчик для пущей наглядности. Теперь зафиксируем некоторый момент времени и каждой точке построенной области поставим в соответствие несвободный вектор, который характеризует:
а) направление движения воздуха в данной точке;
б) и скорость его движения в данной точке – чем выше скорость, тем длиннее вектор. Если в какой-то точке штиль, то ей сопоставляется нулевой вектор.
Множество этих векторов и образует векторное поле скорости ветра в данный момент времени.
Аналогично устроено поле скоростей течения жидкости – так, например, каждой точке реки в некоторый момент времени можно поставить в соответствие вектор, указывающий направление и скорость течения жидкости в этой точке.
Да чего там ветер и река, поле скорости можно смоделировать собственноручно, для этого достаточно взмахнуть рукой. Или даже моргнуть глазом.
…Какой же кошмар! – векторы вокруг нас! В «ужастиках» эту роль играют зомби или живые мертвецы, а в реальности-то вот оно, оказывается как – ВЕКТОРЫ.
С формально-математической точки зрения, векторные поля задают векторными функциями, которые уже «проскакивали» в других темах:
Для «плоского» случая – это векторная функция 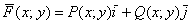
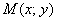
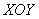
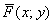
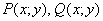
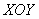
* Далее по умолчанию считаем, что все дела происходят в декартовой системе координат
С трёхмерным пространством всё аналогично:
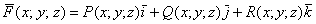
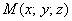
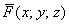
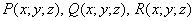
! Обозначения: векторные поля также обозначают буквой 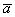
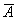
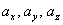
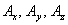
Из вышесказанного давно и очевидно следует, что, по меньшей мере математически, скалярные и векторные поля можно определить и во всём пространстве. Однако с соответствующими физическими примерами я всё же поостерёгся, поскольку таких понятий, как температура, гравитация (или других) ведь где-то может и вовсе не существовать. Но это уже не ужасы, а научная фантастика =) И не только фантастика. Ибо внутри камней ветер, как правило, не дует.
Следует отметить, что векторные поля (те же поля скоростей) с течением времени могут меняться, и поэтому во многих физических моделях рассматривают дополнительную независимую переменную 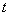
Однако в рамках математики мы ограничимся троицей 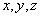
Векторные линии
Если скалярные поля описываются линиями и поверхностями уровня, то «форму» векторного поля можно охарактеризовать векторными линиями. Наверное, многие помнят этот школьный опыт: под лист бумаги помещаются магнит, а наверх (смотрим!) высыпаются железные опилки, которые как раз и «выстраиваются» по линиям поля.
Постараюсь сформулировать попроще: каждая точка векторной линии является началом вектора поля, который лежит на касательной в данной точке: 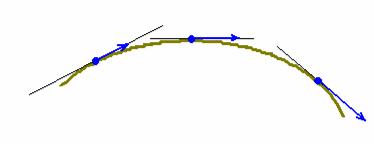
Разумеется, векторы линии в общем случае имеют разную длину, так на приведённом рисунке, при перемещении слева направо их длина растёт – здесь можно предположить, что мы приближаемся, например, к магниту. В силовых физических полях векторные линии так и называют – силовыми линиями. Другой, более простой пример – это гравитационное поле Земли: его силовые линии представляют собой лучи с началом в центре планеты, причём векторы силы тяжести расположены прямо на самих лучах.
Векторные линии скоростных полей называются линями тока. Множество линий тока даёт нам представление о потоке жидкости или газа в данный момент времени. К слову, линия тока и траектория движения частицы – это не одно и то же. Если поле скоростей не меняется с течением времени (например, река с устоявшимся течением), то, да – мусоринки будут плыть по линиям тока. Такое поле называют стационарным, и в нём траектории движения частиц совпадают с линиями тока. Но представьте пыльную бурю – здесь линии тока в каждый момент разные, и поэтому мусоринка будет лететь по своей уникальной траектории, а вовсе не по какой-то конкретной линии тока.
Вообще, многие понятия теории поля пришли из гидродинамики, с чем мы ещё не раз столкнёмся.
Если «плоское» векторное поле задано ненулевой функцией 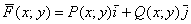
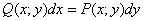
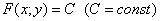
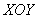
С пространственным векторным полем 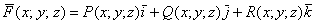
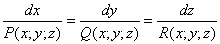
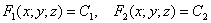
если 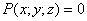
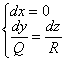
если 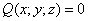
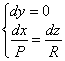
и если 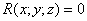
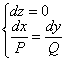
И что-то непозволительно давно у нас не было практики:
Найти силовые линии векторного поля
Решение: в данной задаче 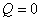
Первый диффур вообще халява: 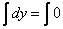
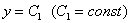
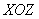
Второй диффур – почти она же:), ну а зачем нам скоропостижные трудности? 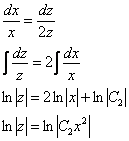
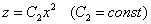
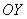
Ответ: искомое множество векторных линий:
Иными словами, здесь в каждой плоскости 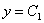
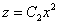
Аналогичная задачка для самостоятельного решения:
Найти силовые линии векторного поля
Охарактеризуйте получившееся множество линий. Кстати, в условии явно не сказано, о каком поле идёт речь – плоском или пространственном. В подобных ситуациях рекомендую решать задачу для пространства – не ошибётесь 😉
Краткое решение и ответ в конце урока.
Векторное поле градиентов
В каких отношениях вы находитесь с производной по направлению и градиентом? …ничего страшного, от ненависти до любви – один шаг =) Напоминаю, что градиент функции в точке – это несвободный вектор, указывающий направление максимального роста функции в данной точке и определяющий скорость этого роста.
Нахождение векторной функции градиентов – есть популярный и распространённый способ получить из скалярного поля поле векторное. При условии существования соответствующих частных производных функции двух и трёх переменных:
Смысл очень прост. Так, если функция 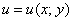
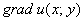
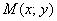
Если функция 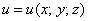
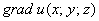
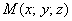
Разберём общую математическую задачу:
Дано скалярное поле 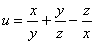
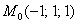
1) составить градиентную функцию скалярного поля;
2) найти градиент поля в точке 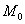
3) вычислить производную по направлению нормального вектора к поверхности 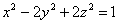
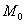
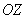
Непосредственно к решению задачи это не относится, но сразу обратим внимание, что скалярное поле не определено на всех трёх координатных плоскостях 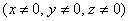
1) Быстренько вспоминаем, как находить частные производные функции трёх переменных:
Составим функцию, которая определяет векторное поле градиентов:
И ещё раз – в чём её смысл? Полученная векторная функция каждой точке 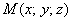
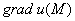
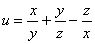
И один из таких векторов нам предстоит найти в следующем пункте:
2) Вычислим частные производные в точке 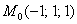
Таким образом: 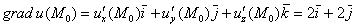
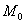
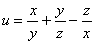
Мерилом же этой максимальной скорости как раз является длина градиента:
3) Вычислим производную по направлению нормального вектора к поверхности 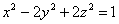
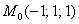
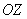
Немного мудрёно, но разобраться немудренО. Во-первых, убедимся, что точка «эм нулевое» действительно принадлежит данной поверхности: 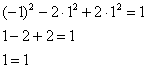
Получено верное равенство. ОК.
Что это за поверхность – нас не интересует, нам важен её нормальный вектор в точке 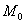
Вспоминаем материал ещё одного урока: вектор нормали к поверхности 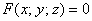
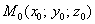
В данном случае:
Но нужный ли это вектор? Как выяснить угол, который он образует с полуосью 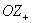
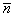
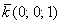
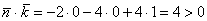
И поэтому нужно выбрать противоположно направленный нормальный вектор:
Заметим заодно, что нормальные векторы в отличие от градиентов – свободны, их задача лишь указать направление.
Вычислим направляющие косинусы данного направления, или, что то же самое – координаты единичного вектора, сонаправленного с вектором 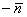
Контроль:
Таким образом, искомая производная по направлению:
Напоминаю, что это значение характеризует скорость роста функции 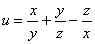
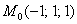
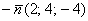
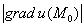
Ответ:
Небольшой пример для самостоятельного решения:
Найти угол между градиентами скалярных полей 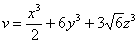
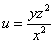
Просто и со вкусом. …Как найти угол? – с помощью того же скалярного произведения. Ну и, очевидно, тут придётся «тряхнуть» многоэтажными дробями и некоторой тригонометрией. Краткое решение и ответ в конце урока.
Что делать, если вам предложено «плоское» скалярное поле 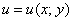
Потенциальное векторное поле
На уроке Криволинейный интеграл по замкнутому контуру я уже подробно рассказал о «плоском» потенциальном поле, и поэтому перед дальнейшим чтением будет крайне полезно окинуть взглядом концовку указанной статьи. Фактически сейчас будет продолжение, где мы разбёрём аналогичную ситуацию в пространстве.
«Потенциальное»…, на ум здесь приходит потенциальная энергия, потенциальные возможности. Так, лежащий на подоконнике кирпич потенциально можно сбросить вниз, и вмятина на земле неиллюзорно продемонстрируют нам ту самую потенциальную энергию. Всё верно, гравитационное поле Земли – это один из ярких примеров потенциального векторного поля.
Вспомним его характерный признак, сбросив с подоконника нашего уютного деревенского домика…, нет, не кирпич, а пёрышко. Из точки 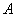
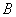
Примечание: возможно, здесь у вас возник вопрос: «но ветер же может приподнимать перо, и тогда работа должна увеличиваться!». Ничего подобного. Физическое понятие работы не подразумевает, что кто-то или что-то «трудится». Если ветер приподнимает перо вверх, то он просто уменьшает абсолютную величину работы силы тяжести.
В физике есть конкретная математическая модель, описывающая гравитационные силы, но в соответствии с направленностью сайта, я приведу только общие формулы. Итак:
Векторное поле 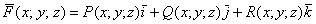
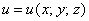
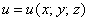
Работа 
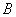
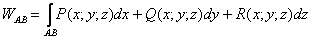
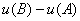
Иными словами, в потенциальном поле имеет значение лишь начальная и конечная точка маршрута. И если эти точки совпадают, то суммарная работа сил по замкнутому контуру 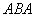
Давайте поднимем пёрышко с земли и доставим его в исходную точку. При этом траектория нашего движения опять же произвольная; можно даже бросить перо, снова его поднять и т.д.
Почему итоговый результат нулевой?
Перо упало из точки «а» в точку «бэ»? Упало. Сила тяжести совершила работу 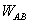
Перо попало обратно в точку «а»? Попало. А это значит, что была совершена точно такая же работа 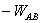
Примечание: в физике знак «минус» символизирует противоположное направление.
Таким образом, суммарная работа сил равна нулю:
Как я уже отмечал, физическое и обывательское понятие работы отличаются. И это различие вам хорошо поможет понять не пёрышко и даже не кирпич, а, например, пианино 🙂
Дружно поднимите пианино и спустите его по лестнице вниз. Потаскайте по улице. Сколько захочется и где захочется. И если никто не вызвал дурку занесите инструмент обратно. Вы поработали? Конечно. До седьмого пота. Но с точки зрения физики никакой работы не совершено.
Словосочетание «разность потенциалов» подмывает рассказать ещё о потенциальном электростатическом поле, но бить током своих читателей как-то уж совсем не гуманно =) Тем более, примеров – непочатый край, ибо потенциальным является любое градиентное поле, коих пруд пруди.
Но легко сказать «пруд пруди»: вот дано нам векторное поле 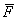
Ротор векторного поля
Или его вихревая составляющая, которая тоже выражается векторами.
Снова возьмём в руки пёрышко и аккуратно отправим его в плавание по реке. Для чистоты эксперимента будем считать, что оно однородно и симметрично относительно своего центра. Ось 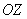
Рассмотрим векторное поле скорости течения (считаем, что оно неизменно во времени), и некоторую точку водной поверхности, над которой находится центр пера.
Если в данной точке перо вращается против часовой стрелки, то поставим ей в соответствие исходящий несвободный вектор, направленный вверх. При этом, чем быстрее вращается перо, тем длиннее этот вектор, …мне почему-то он представляется таким чёрным-чёрным в ярких лучах солнца…. Если вращение происходит ПО часовой стрелке, то вектор «смотрит» вниз. Если же перо не вращается вовсе, то вектор нулевой.
Знакомьтесь – это и есть вектор ротора векторного поля скорости, он характеризует направление «завихрения» жидкости в данной точке и угловую скорость вращения пера (но не направление и не скорость самого течения!).
Совершенно понятно, что роторный вектор есть у всех точек реки (в том числе тех, которые «под водой»), таким образом, для векторного поля скорости течения мы определили новое векторное поле!
Если векторное поле задано функцией 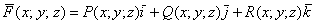
При этом, если векторы роторного поля реки велики по модулю и имеют тенденцию менять направление, то это вовсе не означает, что речь идёт об извилистой и неспокойной реке (возвращаемся к примеру). Такая ситуация может наблюдаться и в прямолинейном русле – когда, например, в середине скорость выше, а у берегов ниже. То есть, вращение пера порождается различными скоростями течения в соседних линиях тока. Но это не единственно возможная причина вращения. Если рядом с рекой стоит экспериментатор и поливает её из шланга, то поле скоростей будет постоянно меняться, и «завихрения» начнутся по той причине, что меняются сами линии тока.
С другой стороны, если роторные векторы коротки, то это может быть и «петляющая» горная речка! Важно, чтобы в соседних линиях тока скорость самого течения (быстрого или медленного) отличалась незначительно. И не было рядом экспериментаторов или каких-нибудь оползней, которые меняют поле скоростей.
И, наконец, отвечаем на поставленный выше вопрос: в любой точке потенциального поля 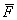
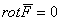
Потенциальное поле также называют безвихревым полем.
Ну и, конечно, наше бренное гравитационное поле. Для следующего опыта хорошо подойдёт любой достаточно тяжёлый и однородный предмет, например, закрытая книга, непочатая банка пива или, кстати, кирпич, который таки дождался своего часа =) Зажмите его торцы руками, приподнимите вверх и аккуратно отпустите в свободное падение. Крутиться он не будет. А если и будет, то это уже ваши «личные усилия» или кирпич попался неправильный. Не поленитесь и проверьте этот факт! Только не бросайте ничего из окна, это уже не перо
После чего с чистой совестью и повышенным тонусом можно вернуться к практическим задачам:
Показать, что векторное поле 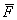
Решение: условие прямо утверждает потенциальность поля, и наша задача состоит в доказательстве этого факта. Найдём роторную функцию или, как чаще говорят – ротор данного поля:
Для удобства выпишем компоненты поля:
и начнём находить их частные производные – их удобно «перебирать» в «роторном» порядке, слева направо:
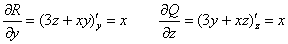
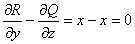
Таким образом: 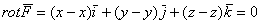
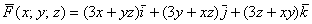
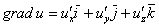
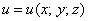
Функцию 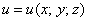
1) Способ первый. Коль скоро так (см. выше), то:
Дальнейший алгоритм напоминает решение дифференциального уравнения в полных дифференциалах, только с бОльшим количеством шагов:
Так как 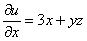
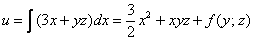
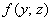
Дифференцируем полученный результат по «игрек»:
Но, с другой стороны 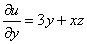
Теперь частным интегрированием (переменных здесь уже две!) находим:
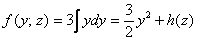
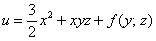
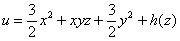
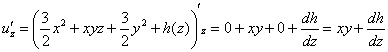
Но с другой стороны, 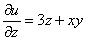
И, наконец, подставляем найдённую функцию 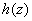
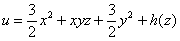
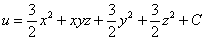
Проверку тут выполнить легче лёгкого, находим частные производные 1-го порядка: 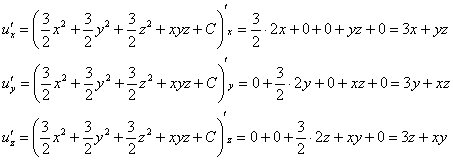
которые совпали с соответствующими компонентами исходного поля 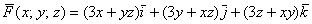
Ну и, наверное, некоторые уже подметили, что равенства частных производных в «роторной» формуле – есть не что иное, как равенства смешанных частных производных 2-го порядка функции 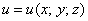
2) Способ второй. Потенциальную функцию можно найти при помощи формулы: 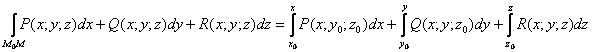
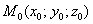
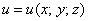
Легко видеть, что этот криволинейный интеграл определяет работу векторного поля 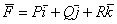
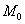
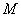
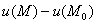
Запишем сумму трёх интегралов для поля 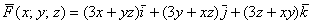
И на этом шаге я по возможности рекомендую выбрать точку 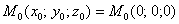
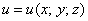
При подстановке верхних пределов интегрирования можно сказать, что вместо «икс» мы подставляем «икс», вместо «игрек» – «игрек», и вместо «зет» – «зет».
Ответ:
Если начало координат выбрать нельзя, то задачу придётся решать в общем виде, в результате чего должна получиться разность 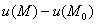
С аналогичной задачей для «плоского» векторного поля можно ознакомиться на уроке Криволинейный интеграл по замкнутому контуру.
Пара полей для самостоятельного решения:
Выяснить, является ли следующие векторные поля потенциальными, и если да, то найти их потенциалы:
а)
б)
Обязано ли поле быть потенциальным в таких задачах? Конечно, нет, и отрицательный ответ – это тоже полноценный ответ. Примерный образец чистового оформления заданий внизу страницы.
Ну что же, теперь пришло время немного отдохнуть и увеличить ротор реки =) А именно нырнуть, искупаться и позагорать на солнце. Чтобы с новыми силами вернуться к столь увлекательной теме, а именно к потоку и циркуляции векторного поля
Спасибо за внимание и до скорых встреч!
Пример 2: Решение: составим и решим систему: 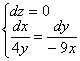
Из 1-го уравнения: 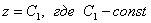
Из 2-го уравнения: 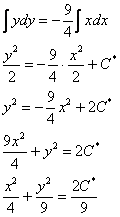
Константу 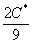
Ответ: 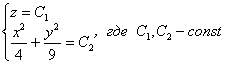
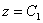
Примечание: если в условии задачи подразумевается «плоское» векторное поле, то векторные линии представляют собой множество эллипсов 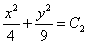
Пример 4: Решение: вычислим частные производные функции 
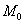
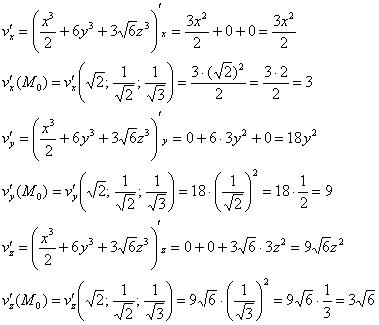
Составим градиент данного скалярного поля в точке 
Аналогично найдём градиент второго скалярного поля: 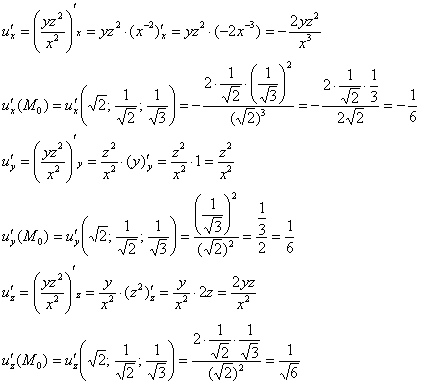
В результате:
Угол 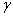
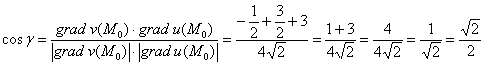
Таким образом:
Ответ:
Пример 6: Решение:
а) проверим, равен ли нулю ротор векторного поля: 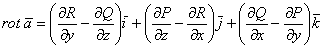
В данном случае: 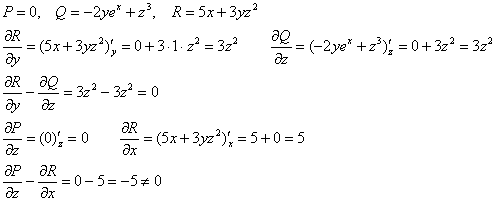
Следовательно,
Ответ: поле 
б) найдём ротор векторного поля: 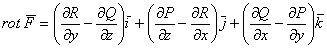
В данной задаче: 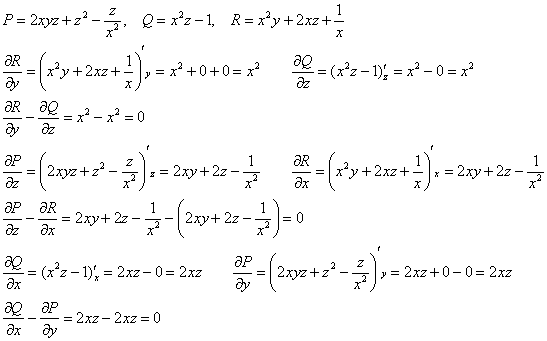
Таким образом: 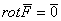
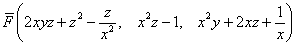
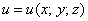
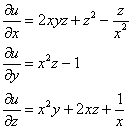
Так как 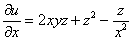
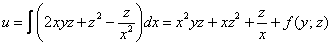
Дифференцируем по «игрек»: 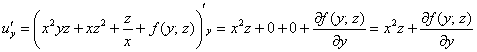
С другой стороны 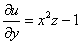
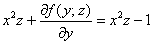
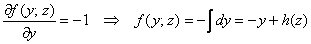
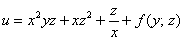
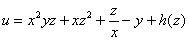
Дифференцируем по «зет»: 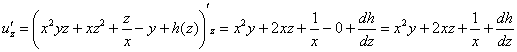
С другой стороны, 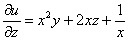
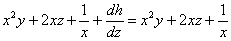
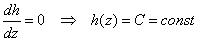
Ответ: поле 
Автор: Емелин Александр
(Переход на главную страницу)