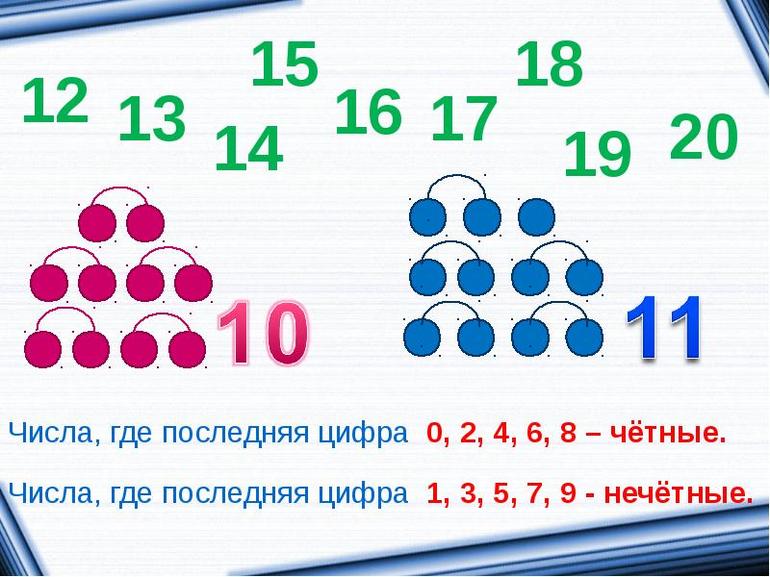
какие есть четные числа
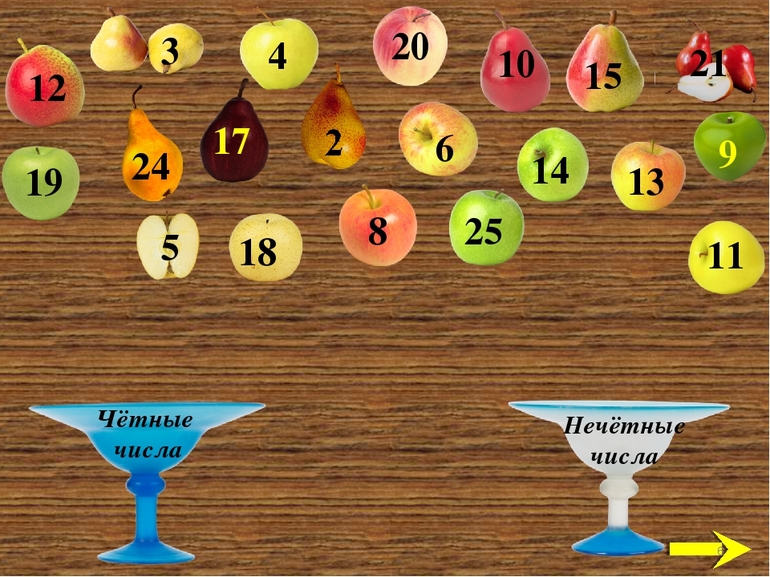
Определить чётное или нечётное число
Сколько чётных и нечётных чисел между.
Теория
Чётное ли число
Чётным является целое число, которое делится на 2 без остатка (нацело).
Все многозначные числа, оканчивающиеся на 0,2,4,6 или 8, являются чётными числами:
Примеры
Чётное ли число 10?
Десять разделилось на два без остатка, следовательно 10 является чётным числом.
После деления единицы на два мы получаем нецелое число, следовательно 1 не является чётным числом.
Чётность нуля
Ноль чётное число, так как оно делится на два без остатка: 0 ÷ 2 = 0
Нечётные числа
Нечетным является целое число, которое не делится на 2 без остатка.
Все многозначные числа, оканчивающиеся на 1,3,5,7 или 9, являются нечётными числами:
Пример
Для примера рассмотрим число 67. Так как оно заканчивается цифрой 7 (нечётной), уже можно утверждать, что оно нечётное. Для пущей уверенности разделим 67 на два:
67 ÷ 2 = 33.5, то есть 33 и остаток 1 (67 = 33 ⋅ 2 + 1)
Окончательно делаем вывод, что число 67 является нечётным числом.
Сколько чётных и нечётных чисел в ряду
Сколько чётных и нечётных чисел находится в ряду между n и m?
Если n и m разные по чётности
Если n и m разные по чётности числа, то есть одно из них четное, а второе нечётное, то количество чётных и нечётных чисел в ряду одинаковое:
Пример
Возьмём ряд чисел между n = 22 и m = 31:
22, 23, 24, 25, 26, 27, 28, 29, 30, 31
Определим количество чётных и нечётных чисел в этом ряду.
Так как 22 и 31 являются числами разной чётности делаем вывод, что чётных и нечётных чисел в данном ряду поровну:
5 чётных и 5 нечётных
| 22 | 24 | 26 | 28 | 30 |
| 23 | 25 | 27 | 29 | 31 |
Если n и m чётные
Если n и m чётные числа, то чётных чисел в ряду будет на одно больше, чем нечётных:
Пример
Возьмём ряд чисел между n = 10 и m = 20:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Определим количество чётных и нечётных чисел в этом ряду.
6 чётных и 5 нечётных
| 10 | 12 | 14 | 16 | 18 | 20 |
| 11 | 13 | 15 | 17 | 19 |
Если n и m нечётные
Если n и m нечётные числа, то чётных чисел в ряду будет на одно меньше, чем нечётных:
Пример
Возьмём ряд чисел между n = 11 и m = 19:
11, 12, 13, 14, 15, 16, 17, 18, 19
Определим количество чётных и нечётных чисел в этом ряду.
Четные числа
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]
Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…
Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…
Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
Содержание
Признак чётности
Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.
Арифметика
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.
В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
Четные и нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
ЧИСЛА — ♥ ♠ Значение сна зависит от того, где именно и в каком виде вы видели приснившееся вам число, а также от его значения. Если число было в календаре это предупреждение о том, что в этот день вас ждет важное событие, которое перевернет всю вашу… … Большой семейный сонник
«Сакральный» смысл чисел в верованиях и учениях — К материалу «07.07.07. Влюбленные всего мира поверили в магию чисел» С глубокой древности числа играют важную и многогранную роль в жизни человека. Древние люди приписывали им особые, сверхъестественные свойства; одни числа сулили… … Энциклопедия ньюсмейкеров
АДДИТИВНАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории чисел, в к ром изучаются задачи о разложении целых чисел на слагаемые заданного вида, а также алгебраич. и геометрич. аналоги таких задач, относящиеся к полям алгебраич. чисел и к множествам точек решетки. Эти задачи наз.… … Математическая энциклопедия
Счастливое число — В теории чисел счастливое число является натуральным числом множества генерируемое «решетом», аналогичным решету Эратосфена, которое генерирует простые числа. Начнем со списка целых чисел, начиная с 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,… … Википедия
НУМЕРОЛОГИЯ — методы определения скрытых истин с помощью толкования чисел. В основе нумерологии лежит идея о том, что каждое число является символом неких понятий. Например, 1 это единство, Бог, начало и неделимость; 2 двойственность, разделение, анализ,… … Символы, знаки, эмблемы. Энциклопедия
В мире чисел. Чётные и нечётные
Чёт счастливым
И красивым,
Слабым только лишь нечёт!
Но, редея,
Холодея
Чёт в нечёт перетечёт!
Если вы ещё не знаете, то я открою вам большой секрет – мы живём в МИРЕ ЧИСЕЛ. Они сопровождают нас до нашего появления на свет, и продолжают оставаться с нами, когда мы перебираемся в мир иной. Одна из книг Библии так и называется: «Числа».
Наука доказала, что считать умеют многие животные, начиная с мелких пташек до человекообразных обезьян. И только человек может уловить то общее, что объединяет разные предметы, к примеру, три камня, три пальмы или трёх слонов. За ними стоит общее число. Этот факт дал толчок человеку к росткам абстрактного мышления, что в дальнейшем породило математику, заслуженно названную царицей наук.
Самая распространённая система исчислений – десятичная, по числу пальцев рук, но есть и множество других. Всё началось с целых чисел. Если расположить числа в ряд: 1, 2, 3, 4…, и так далее, то его можно продолжать до бесконечности. Учитывая природный характер чисел, ряд назвали натуральным. Помимо целых чисел, в него входят и рациональные числа в виде дробей с конечным значением. Но есть и иррациональные числа, которые не имеют конечного точного значения. Если представить натуральный ряд в виде линейки, то она будет ещё и сплошной от чисел, без малейших зазоров.
Со временем открыли и «ноль», когда число не имеет значения. Он является истинным началом натурального ряда. А затем поняли, что числа бывают не только положительными, но и отрицательными. Воображаемая линейка будет бесконечной в обе стороны с нулём посередине.
На этом картина чисел не остановилась, когда обнаружили так называемые мнимые числа, то есть такие, которые есть, но каких будто нет. Если от воображаемой линейки провести вертикальную линию, то она будет до бесконечности заполнена мнимыми числами. Но и это ещё не всё, когда открыли комплексные числа, состоящие из действительных и мнимых чисел, а они заполнят всё поле чисел между их рядами. И это только в двух измерениях! А их множество!
Если я вас не утомил, то продолжим двигаться дальше, оставив математикам пользоваться всем множеством названных чисел.
А пока рассмотрим чётные и нечётные числа. Конечно, это относится только к целым числам, поскольку частично чётных не бывает. Чётные числа составляют половину всех натуральных чисел и также бесконечны.
В большинстве стран номера домов на обеих сторонах улицы чётные либо нечётные. Чтобы разгрузить улицы от автотранспорта, в некоторых городах в отдельные дни разрешено ездить машинам с чётными или нечётными номерами.
Живым дарят нечётное число цветов, а мёртвым – чётное. Алла Пугачёва пела, как художник один подарил актрисе миллион роз, то есть чётное число. Естественно, что после этого она дала дёру.
Однако у других народов, к примеру, китайского, отношение к нечётным числам как к дурным.
Вопросы для любителей математики. Испытайте себя:
Чётные и нечётные числа в нумерологии
Что означают чётные и нечётные числа в духовной нумерологии. В изучении языка чисел это очень важная тема! Чем по своей сути чётные числа отличаются от нечётных чисел?
Нечётные числа в нумерологии — солнечные, мужской природы, кислотные, электрические, динамичные. При группировании нечётных чисел, одно число останется без своей пары (1 и 3; 5 и 7; 9). Эти числа являются слагаемые (их складывают с чем-либо).
Чётные числа — лунные, женской природы, щелочные, магнетические, статичные. Числа данной группы вычитаемые или уменьшаемые. Они статичны и остаются без движения, потому что имеют чётные группы пар (2 и 4; 6 и 8).
Чётные числа
Общеизвестно, что чётные числа — те числа которые делятся на два. А что означают чётные числа относительно духовной нумерологии? Какова нумерологическая суть «деления на два»? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У цифры 2 несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе. надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Нечётные числа
Нечётными называют числа, которые не делятся на два. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное. Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел, никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Возьмём для примера число 3 — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них.
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел.
Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь.
Арифметические свойства
Четными называют числа, которые при делении на 2 образуют целое число. Нечетные при том же действии дают результат с остатком (дробное число). Чтобы быстро проверить на четность двузначную цифру, нужно определить параметр для последней его цифры в десятичной записи. Если она делится на два, число является четным, в противном случае — нечетным. Метод работает для любых многозначных чисел.
Арифметические правила четных и нечетных чисел при различных операциях описаны древнегреческим математиком Пифагором до нашей эры и используются для вычислений современниками. Они помогают составлять формулы для оптимизированных расчетов в задачах с большим рядом переменных. Алгоритмы многих онлайн-калькуляторов запрограммированы с помощью таких функций.
Закономерности арифметических операций с целыми числами:
Формула четного числа: m = 2k. Формула нечетного числа: m = 2k + 1.
При уменьшении или увеличении четного числа на единицу получается нечетное и наоборот. При начертании оси с нулем в центре будет сохраняться чередование четных и нечетных чисел. Наглядно продемонстрировать феномен школьникам можно, предложив записать последовательный ряд четных чисел через запятую.
Характеристика парности у ноля
Не бывает целых чисел, которые не принадлежат к одной из групп по признаку кратности двум. Ноль, который разделяет отрицательные и положительные значения последовательного ряда, не является целым. Из-за этого большинство предполагает, что ноль стоит особняком, т. е. не относится ни к одному виду или же одновременно представляет оба.
В науке ноль — это аддитивный нейтральный элемент четной группы. Он является логическим началом для рекурсии последовательного ряда кратных двум объектов. Исследования, проведенные в учебных заведениях Великобритании, показали, что 2/3 преподавателей не знают верного ответа, а ученики пятого класса ошибаются реже, чем из шестого и старше.
Признаки четности ноля:
Маленьким слушателям легче пояснить феномен с помощью двух таблиц — по одной для каждой группы. Элементы кратных схематически изображаются в первом столбце, во втором — остаток. Олицетворяемая нолем пустота при делении на два остается пустотой, что соответствует признаку кратности двум. Вышеприведенный список доказательств содержит другие примеры для наглядной демонстрации логики принадлежности знака к группе элементов, кратных двум.
Свойства группы для вычислений
Когда требуется вычислить сумму множества слагаемых из натурального ряда последовательных нечетных чисел, можно отказаться от длительных монотонных операций. Известно, что сумма любого количества элементов всегда соответствует квадрату их количества. Проверку можно осуществить путем сложения двух, трех и четырех элементов последовательного ряда. Аналогичное выражение можно составить для любого количества слагаемых.
Алгоритм оптимизированного решения:
Количество складываемых элементов последовательного ряда некратных двум числительным всегда соответствует квадратному корню суммы.
Примеры логических задач для решения через характеристику парности:
Ответ на каждую из задач можно получить методом проб и подбора. Понимание законов парности позволяет существенно сократить время на поиск верного решения. Школьникам нравится изящное решение головоломки о маленьком кузнечике. Детям сообщают, что за один скачок он преодолевает 1 метр. Учащимся предлагают доказать, что насекомое совершило парное количество прыжков, если в результате движений оно оказалось в исходной точке.
Ответ становится очевидным при понимании, что пройденный путь, равен расстоянию, которое необходимо пройти для возвращения к стартовой позиции. Таким образом суммарное расстояние обязано быть парным.
История и значение в культуре
Неоценимое влияние на развитие арифметики оказали труды Пифагора. Ученый посвятил много труда и времени, чтобы выявить закономерности свойств чисел и объединить их в логичную систему. Математические законы и наблюдения он связал с мировосприятием и теорией самопознания человека.
Каждой цифре математик отвел свое значение. Нечетные обладают более сильными, активными характеристиками. Именно они в воссозданной мистической системе являлись олицетворением мужского начала, динамики и солнца. Четные же, наоборот, олицетворяли женское естество, статичность и луну.
Аналогичное деление характерно для китайской философии, в которой нечетные числительные относят к светлой мужской субстанции Ян, а Инь — к теневому, негативному, женскому. В учении о материи тайцзи противоположности представлены как единые и неделимые стороны одного целого.
У каждого этноса существуют свои поверья. Самое популярное суеверие у славян запрещает преподносить букеты с парным количеством цветов. В США и Европе такой подарок, наоборот, трактуется как пожелание счастья и благополучия. Нечетность приглашенных гостей, дней празднования, даты события также считается обязательным по свадебным традициям Руси.
Практическое применение
Возможность разделить все числительные на парные и непарные широко используется в повседневной жизни. В зависимости от того, кратен ли двум порядковый номер месяца, по правилам дорожного движения может быть запрещена или разрешена стоянка в определенных зонах. Четные и нечетные недели помогают запомнить расписание вузов с многочисленной аудиторией.
В расписании железнодорожных поездов на кратности двум числа месяца завязаны маршруты с расписанием через день. Чтобы не нарушать установленный порядок, после 31 числа поезд может пропустить один выезд. Тот же принцип используется для нумерации вагонов — парность содержит информацию о направлении пути. В плацкартах и купе места с верхними полками всегда обозначены четным числом, а нижние — нечетным.
Парность строк помогает проверить созвучность стиха поэтам. Если мысленно пронумеровать слоги, можно подобрать слово в соответствии с ритмом произведения, так как ударные и безударные гласные являются основным ориентиром.