какие задачи называют комбинаторными

КОМБИНАТОРИКА

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n₁ способами, второе действие n₂ способами, третье – n₃ способами и так до k-го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены:

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

.

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

.

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

.

Перестановки без повторений. Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

Источник

Мерзляк 5 класс — § 24. Комбинаторные задачи

Вопросы к параграфу

1. Какие задачи называют комбинаторными?

Комбинаторные задачи — это задачи, решение которых требует рассмотрения и подсчёта все возможных случаев (всех возможных комбинаций).

2. Как называют схему, с помощью которой удобно и наглядно решать комбинаторные задачи?

Дерево возможных вариантов.

Решаем устно

1. Одним слоем бумаги оклеили куб, длина ребра которого равна 3 дм. Сколько квадратных дециметров бумаги потребовалось на оклеивание куба?

Найдём площадь поверхности куба:

S = 6a² = 6 • 3² = 6 • 9 = 54 (дм²) — бумаги потребовалось для оклеивания куба.

2. Объём прямоугольного параллелепипеда равен 240 см³. Какая из следующих троек чисел может задавать измерения этого параллелепипеда:

1) 4 см, 6 см, 12 см

4 • 6 • 12 = 24 • 12 = 288 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.

2) 5 см, 6 см, 8 см

5 • 6 • 8 = 30 • 8 = 240 (см³) — да, эти числа могут быть измерениями данного прямоугольного параллелепипеда.

3) 3 см, 5 см, 10 см

3 • 5 • 10 = 15 • 10 = 150 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.

4) 10 см, 10 см, 24 см

10 • 10 • 24 = 100 • 24 = 2 400 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.

Ответ: числа 5 см, 6 см и 8 см.

3. Сколько центнеров пшеницы можно засыпать в бункер, имеющий форму прямоугольного параллелепипеда, если его длина равна 8 м, ширина — 2 м, высота — 1 м, а масса 1 м³ зерна составляет 8 ц?

1) 8 • 2 • 1 = 16 (м²) — объём бункера.

2) 16 • 8 = 128 (ц) — пшеницы можно засыпать в бункер.

Ответ: 128 центнеров.

4. Что больше и на сколько:

1) квадрат суммы чисел 4 и 3 или сумма их квадратов

(4 + 3)² > 4² + 3²
7² > 16 + 9
49 > 25

2) разность квадратов чисел 10 и 8 или квадрат их разности

10² — 8² > (10 — 8)²
100² — 64² > 2²
36 > 4

3) разность кубов чисел 5 и 3 или куб их разности

5³ — 3³ > (5 — 3)³
125 — 27 > 2³
98 > 8

Упражнения

645. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 3 (цифры могут повторяться).

Таких двузначных чисел всего 9:

646. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 0 (цифры могут повторяться).

Таких двузначных чисел всего 6:

647. У ослика Иа-Иа есть три надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько у ослика Иа-Иа есть вариантов сделать подарки своим друзьям?

Решим задачу при помощи схемы «Дерево возможных вариантов».

Итак, у нас получилось шесть возможных вариантов:

Винни-Пуха

Кролик

Вариант 1

Вариант 2

Вариант 3

648. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0, 1 и 2?

Таких двузначных чисел всего 4:

649. В футбольном турнире участвуют команды 5 «А» класса, 5 «Б» класса и 5 «В» класса. Сколько существует способов распределения первого и второго мест среди этих команд? Решение какой задачи из номеров 645—648 аналогично решению этой задачи?

Решим задачу при помощи схемы «Дерево возможных вариантов».

Итак, у нас получилось шесть возможных вариантов (последовательно места, занятые 5″А», 5″Б» и 5″В»):

Итак, у нас получилось шесть возможных вариантов (последовательно цвет шарика для Винни-Пуха, Пятачка и Кролика):

Вариант 1

Вариант 2

Вариант 3

Задача аналогична задаче № 647.

650. Запишите все трёхзначные числа, для записи которых используются только цифры (Цифры не могут повторяться.):

1) 3, 4 и 6

2) 4, 7 и 0

651. Сколько различных трёхзначных чисел можно составить из цифр (Цифры могут повторяться.):

1) 1 и 2

2) 0 и 1

652. Запишите все двузначные числа, в записи которых используются только цифры 2, 4, 9 и 0. (Цифры могут повторяться.)

653. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке возрастания?

654. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке убывания?

655. Сколько существует двузначных чисел, сумма цифр которых равна 5?

Всего 5 чисел: 14, 23, 32, 41, 50.

656. Сколько двузначных чисел, сумма цифр которых равна чётному числу, можно составить из цифр 1, 2, 3, 4 (цифры могут повторяться)?

Всего 8 чисел: 11, 13, 22, 24, 31, 33, 42, 44.

657. Сколько двузначных чисел, сумма цифр которых равна нечётному числу, можно составить из цифр 0, 1,2, 3?

Всего 6 чисел: 10, 12, 21, 23, 30, 32.

658. Кот Базилио и лиса Алиса решили украсть золотой ключик, который хранится в каморке папы Карло. Чтобы туда проникнуть, нужно подобрать двузначный код. Им известно, что дверь в каморку закрывает Буратино, который знает пока что только четыре цифры: 0, 1, 2 и 3. Какое наибольшее количество вариантов придётся перебрать коту и лисе, чтобы открыть дверь?

Итак, возможное количество вариантов кода — 16.

Ответ: 16 вариантов.

659. Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?

Если P = 24 см, то сумма длин сторон равна 24 : 2 = 12 см.

Существует 6 возможных вариантов таких прямоугольников. Длины сторон у них должны быть:

Ответ: 6 прямоугольников.

660. У Ани есть 30 одинаковых кубиков. Сколько различных прямоугольных параллелепипедов она может из них составить, если для построения одного параллелепипеда надо использовать все имеющиеся 30 кубиков?

Если V = 30, то можно подобрать 5 вариантов постройки прямоугольного параллелепипеда из одинаковых кубиков:

661. На прямой отметили четыре точки А, В, С и D. Сколько отрезков с концами в отмеченных точках можно провести? Какой из рисунков § 24 помогает решить эту задачу?

Для решения этой задачи можно ориентироваться на рисунок 184 § 24:

Но лучше сделать свой рисунок для этой конкретно задачи:

662. Подножие горы и её вершину связывают три тропы. Сколько существует маршрутов, ведущих от подножия к вершине и затем вниз к подножию?

Нарисуем эти три маршрута схематично, изобразив их в виде лучей, выходящих из единой точки, где:

Тогда возможные следующие варианты маршрутов (начало маршрута — вершина — конец маршрута):

Итого — 9 вариантов маршрутов.

663. Спортивной команде предлагают футболки трёх цветов — красного, зелёного и синего, а шорты двух цветов — белого и жёлтого. Сколько вариантов выбора формы есть у команды?

Форма

Синие

Шорты

БелыеКрасная футболка

белые шортыЗелёная футболка

белые шортыСиняя футболка

белые шортыЖёлтыеКрасная футболка

жёлтые шортыЗелёная футболка

Итак, возможное количество вариантов формы — 6.

664. У Тани есть четыре платья и две пары туфель. Сколько у Тани есть вариантов выбора наряда?

Наряд

Туфли

1Платье № 1

Туфли № 1Платье № 2

Туфли № 1Платье № 3

Туфли № 1Платье № 4

Туфли № 12Платье № 1

Туфли № 2Платье № 2

Туфли № 2Платье № 3

Итак, возможное количество вариантов нарядов — 8.

665. В отряде космонавтов есть три пилота и два инженера. Сколько существует способов составить экипаж, состоящий из одного пилота и одного инженера?

Экипаж

Инженеры

1Пилот 1

Инженер 12Пилот 1

Итак, возможное количество вариантов нарядов — 6.

666. На рисунке 185 изображён план одного района города. Отрезками изображены улицы. Сколько существует маршрутов из точки А в точку В, если передвигаться разрешено по улицам, идущими вверх или вправо?

Существуют следующие варианты маршрутов:

Итак, возможное количество вариантов маршрутов — 6.

667. В записи 1 * 2 * 3 * 4 вместо каждой звёздочки можно поставить один из знаков «+» или «•». Чему равно наибольшее значение выражения, которое можно получить?

Наибольшее значение выражения можно получить, если расставить знаки в таком порядке:

1 + 2 • 3 • 4 = 1 + 6 • 4 = 1 + 24 = 25.

Упражнения для повторения

668. Расстояние между двумя сёлами равно 28 км. Из этих сёл одновременно в одном направлении выехали мотоциклист и автобус. Автобус ехал впереди со скоростью 42 км/ч, а мотоциклист ехал со скоростью 56 км/ч. Через сколько часов после начала движения мотоциклист догонит автобус?

1) 56 — 42 = 14 (км/ч) — скорость, с которой мотоциклист догоняет автобус — скорость сближения.

2) 28 : 14 = 2 (часа) — время, за которое мотоциклист догонит автобус.

669. Решите уравнение:

670. 1) Одно из слагаемых в 14 раз больше другого. Во сколько раз их сумма больше меньшего слагаемого?

Пусть х — первое слагаемое. Тогда второе слагаемое равно 14х.

(14х + х) : х = 15х : х = 15

2) Вычитаемое в 12 раз больше разности. Во сколько раз уменьшаемое больше разности?

Пусть х — разность, тогда вычитаемое равно 12х, а уменьшаемое равно (12х + х).

(12х + х) : х = 13х : х = 13

671. На ферме есть 156 коров, каждая из которых даёт в день 12 л молока. Молоко с фермы вывозят в бидонах ёмкостью 40 л. В некоторый день на ферме было в наличии 42 пустых бидона. Хватит ли бидонов, чтобы вывезти с фермы надоенное за день молоко?

1) 156 • 12 = 1 872 (литра) — молока надаивают на ферме за 1 день.

2) 42 • 40 = 1 680 (литров) — молока помещается в 42 пустых бидона.

Ответ: Нет, не хватит.

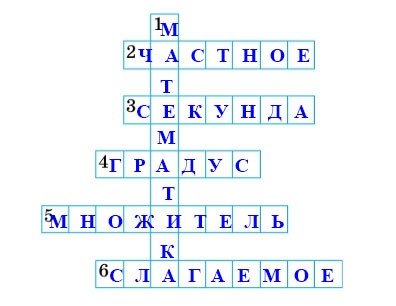
672. Решите кроссворд.

По горизонтали:

2. Результат арифметического действия (Частное)
3. Единица измерения времени (Секунда)
4. Единица измерения углов (Градус)
5. Компонент умножения (Множитель)
6. Компонент сложения (Слагаемое)

По вертикали:
1. «Царица наук» (Математика)

Задача от мудрой совы

673. В классе 30 учащихся. Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?

1) Если половина всех девочек сидят с мальчиками, значит вторая половина девочек сидит друг с другом по двое за партой. Значит половина девочек — это чётное количество человек.

2) Если половина девочек — это чётное количество человек, то общее количество девочек (две половины) также будет чётным числом.

3) Предположим, что условие задачи выполнимо и половину мальчиков можно посадить с девочками. Это значит, что другая половина мальчиков будет сидеть по двое за партой. То есть половина мальчиков также должно быть чётным числом.

4) Половина мальчиков и половина девочек — это ровно половина класса. По нашему предположению это чётное количество человек, так как и половина мальчиков, и половина девочек чётные числа.

5) Но мы знаем, что в классе 30 учащихся, а половина от 30 человек — это 15 человек — нечётное число. Значит наше предположение о мальчиках было неверно и их нельзя посадить так, чтобы половина мальчиков сидела с девочками.

Источник

Комбинаторные задачи

Комбинато́рика (Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисление элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения, например в информатике и статистической физике.

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Иногда под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.

Содержание

Примеры комбинаторных конфигураций и задач

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

Примерами комбинаторных задач являются:

Разделы комбинаторики

Перечислительная комбинаторика

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определенные ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Типичным примером задач данного раздела является подсчете количества перестановок (см. выше). Число перестановок n-элементного множества равно факториалу числа n, то есть n!. Другой пример — известная Задача о письмах.

Структурная комбинаторика

К данному разделу относятся некоторые вопросы теории графов, а также теории матроидов.

Экстремальная комбинаторика

Примером этого раздела может служить следующая задача: какова наибольшая размерность графа, удовлетворяющего определенным свойствам.

Теория Рамсея

Теория Рамсея изучает наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующее:

в группе из 6 человек всегда можно найти три человека, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

В терминах структурной комбинаторики это же утверждение формулируется так:

в любом графе с 6 вершинами найдется либо клика, либо независимое множество размера 3.

Вероятностная комбинаторика

Этот раздел отвечает на вопросы вида: какова вероятность присутствия определенного свойства у заданного множества.

Топологическая комбинаторика

Аналоги комбинаторных концепций и методов используются и в топологии, при изучении дерева принятия решений, частично упорядоченных множеств, раскрасок графа и др.

См. также

Литература

Полезное

Смотреть что такое «Комбинаторные задачи» в других словарях:

КОМБИНАТОРНЫЕ ЗАДАЧИ — класс и ческ незадачи выбора и расположения элементов конечного множества, имеющие в качестве исходной нек рую формулировку развлекательного содержания типа головоломок. Одной из классических К. з., фигурирующей еще в мифах Древнего Востока,… … Математическая энциклопедия

Комбинаторные методы решения экономических задач — [com­binatorial methods in economics] совокупность (не вполне определенная) методов, основанных на идеях комбинаторики отдела математики, изучающего вопросы, связанные с размещением и взаимным расположением частей конечного множества объектов. С… … Экономико-математический словарь

комбинаторные методы решения экономических задач — Совокупность (не вполне определенная) методов, основанных на идеях комбинаторики отдела математики, изучающего вопросы, связанные с размещением и взаимным расположением частей конечного множества объектов. С помощью этих методов решаются… … Справочник технического переводчика

КОМБИНАТОРНЫЙ АНАЛИЗ — комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия

История комбинаторики — освещает развитие комбинаторики раздела конечной математики, который исследует в основном различные способы выборки заданного числа m элементов из заданного конечного множества: размещения, сочетания, перестановки, а также перечисление и смежные… … Википедия

Удовлетворение ограничений — Содержание 1 Введение 2 История 3 Примеры задач удовлетворения ограничений … Википедия

ВЕРОЯТНОСТЕЙ ТЕОРИЯ — занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера

Нейронная сеть Хопфилда — Нейронная сеть Хопфилда полносвязная нейронная сеть с симметричной матрицей связей. В процессе работы динамика таких сетей сходится (конвергирует) к одному из положений равновесия. Эти положения равновесия являются локальными минимумами… … Википедия

ВЕРОЯТНОСТЕЙ ТЕОРИЯ — математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных к. л. образом с первыми. Утверждение о том, что к. л. событие наступает с вероятностью, равной, напр., 1/2, еще не… … Математическая энциклопедия

Псевдополиномиальный алгоритм — полиномиальный алгоритм, проявляющий экспоненциальный характер только при очень больших значениях числовых параметров. Более строгое определение выглядит так. Пусть M(z) – некоторая функция, задающая значение числового параметра индивидуальной… … Википедия

Источник